锥头射弹侵彻金属薄板极限速度分析*
严 平 康 德
(1.海军工程大学 武汉 430033)(2.92207部队 石家庄 050300)
锥头射弹侵彻金属薄板极限速度分析*
严 平1康 德2
(1.海军工程大学 武汉 430033)(2.92207部队 石家庄 050300)
论文将锥头射弹侵彻贯穿金属薄靶板的耗能分为整体和局部耗能两部分。基于空腔膨胀理论,给出了靶板对射弹的阻力表达式,然后计算出局部变形耗能。根据量纲分析和相似原理,由搜集到的弹道试验数据拟合求得整体变形耗能,推出了射弹穿透金属靶板的弹道极限公式。并将模型预测结果和数值仿真分析的结果进行了比较分析。
锥头射弹; 侵彻贯穿; 金属薄靶板; 弹道极限
Class Number TU511
1 引言
射弹侵彻贯穿金属靶板一直是民用和军用工程防护、武器设计关心的重要问题。弹道极限速度是反映靶板抵抗弹体侵彻贯穿能力的综合性指标,在设计、评估防护结构和装甲防护等方面都是至关重要的。目前,确定弹道极限速度的途径主要有试验研究、工程模型和数值模拟。试验研究耗资大,其经验公式具有很大的局限性;数值模拟可较好地模拟侵彻贯穿过程,但需耗费大量机时。因此,工程模型方法仍然是研究侵彻问题的重要途径。但目前的分析模型过于复杂且参数较多,不适合工程计算。建立实用、简化的弹道极限速度的分析模型仍然是一个值得进一步研究的难题。
当射弹为刚性弹时,射弹侵彻靶板所损失的动能将主要转化为靶板的塑性变形耗能[1],靶板的塑性变形耗能又可分为局部和整体两部分。本文基于准静态柱形空穴膨胀理论结合靶板的自由表面效应修正函数,给出了靶板对射弹的阻力表达式,然后计算出局部变形耗能。根据量纲分析和相似原理,由弹道极限试验数据拟合求得靶板的整体耗能表达式,推出了锥头射弹穿透金属靶板的耗能公式和弹道极限公式。模型预测结果与数值模拟进行了比较,发现二者吻合得较好。
2 金属靶板抵抗射弹侵彻的理论模型
2.1 靶板阻力公式
Hill[2]通过研究柱形空穴在无限体中的膨胀,给出了刚性-理想塑性不可压缩材料的空穴表面应力为
(1)
式中E为弹性模量,σy为金属材料的准静态屈服应力。
对于薄靶的穿透,由于靶体材料扩展方向上的厚度是有限的,需要考虑靶体背面的自由表面效应,孙炜海[3]构造了一个准静态柱形空穴膨胀理论的自由表面效应修正函数,即
(2)
其中N为待定常数,H为板厚,d为射弹直径,r为射弹锥角。这样,则锥头射弹穿透薄靶的过程中,靶体材料对射弹表面法向的阻力为
σn=fσ=∂σy
(3)
其中系数∂定义为
(4)
2.2 局部耗能分析
本文所研究弹体头部长度Ln大于靶厚H,图1为锥头射弹侵彻贯穿靶板的示意图。侵彻过程可分为三个不同的阶段:从弹头顶部侵入至弹顶到达靶板背面结束为第一阶段,从弹顶部分穿出靶体背面至弹肩到达靶板正面前为第二阶段,弹头部分逐渐从靶体背面穿出,直至完全贯穿靶体为第三阶段。
通过积分可以得出不同阶段射弹所受的轴向阻力为
(5)
式中z为射弹在前进方向上的侵入深度,σn为弹头表面所受的压力,μ为弹-靶间的动态摩擦系数,文献中关于锥头弹侵彻和贯穿金属勒板的摩擦系数常取0~0.05之间[4~5]。
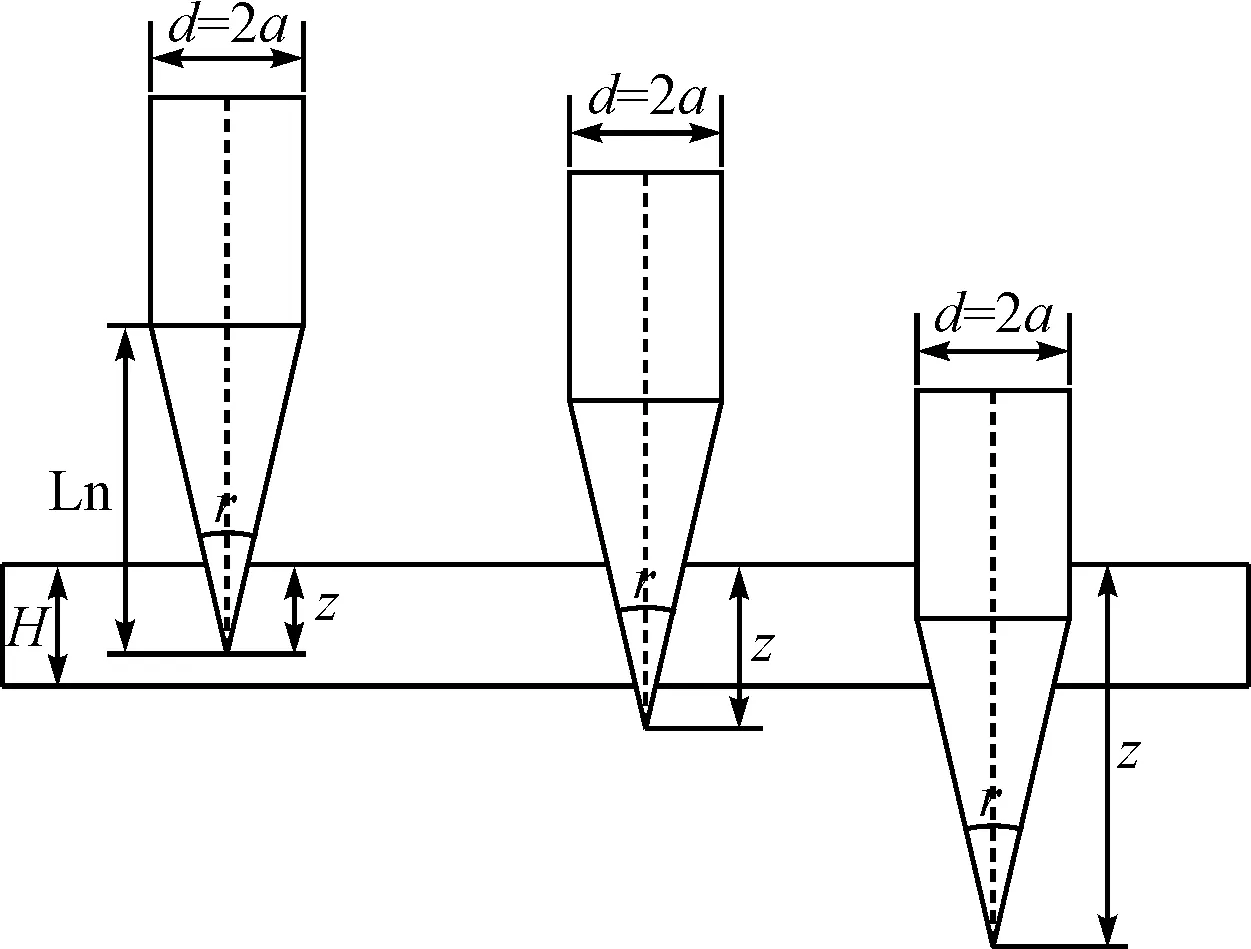
图1 锥形弹体侵彻贯穿金属靶板示意图
由功能原理,三个阶段力做的功之和为射弹穿透靶板时的局部耗能WJ,即
WJ=W1+W2+W3
(6)
而三个阶段耗能分别为
(7)
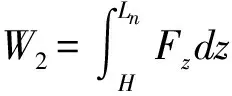
(8)
(9)
把式(7)~式(9)代入式(6),得
(10)
2.3 整体变形耗能
整体耗能主要是靶板的整体弯曲和拉伸变形耗能等,靶板整体塑性变形耗能Wz的计算比较复杂,涉及变量较多,不便推广应用。射弹最小穿透能量E包括整体变形耗能和局部变形耗能,即
(11)
为了简化计算,将式(11)后半部分与式(10)改写成无量纲形式:
(12)
靶板的整体变形耗能一般与冲击速度、着靶姿态、弹体和靶板材料的特性、几何形状等因素有关。由量纲分析和相似原理[6],靶板的整体变形耗能可表示为
(13)
式中,υ0和φ分别为撞击速度和射弹入射角。ρ、ν、σ分别为密度、泊松比、屈服应力,下标p和t分别表示射弹和靶板。
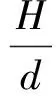
(14)
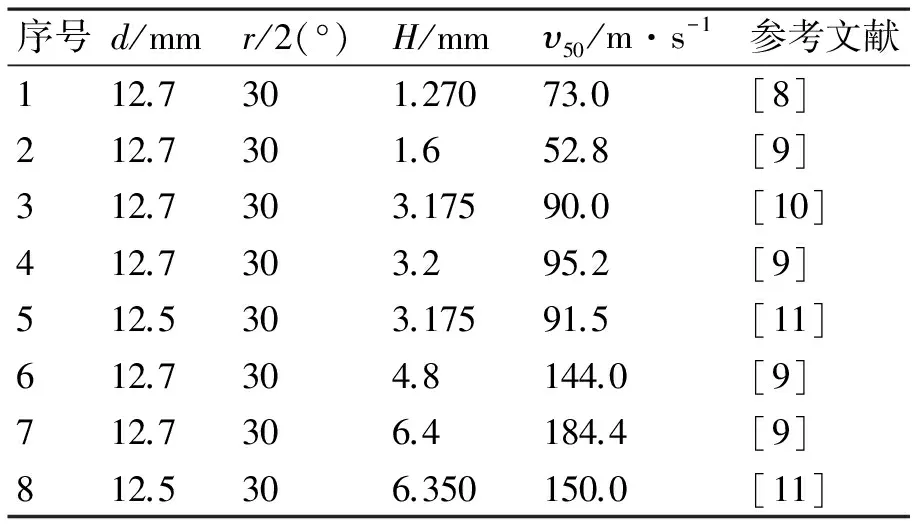
式中,a、b为经验常数。表1给出了金属靶板弹道试验数据。由表1数据和式(11)、式(12)、式(14),用最小二乘法求得:a=6.984,b=2.256。求解结果如图2所示。

图2 无量纲整体变形耗能实验结果拟合图
将a、b代入式(14),得无量纲整体变形耗能:
(15)
2.4 弹道极限速度计算模型
由式(12)、式(15)得无量纲最小穿透耗能公式为
(16)
由式(11)、(16)可得靶板的弹道极限速度为
(17)
3 极限速度模型的仿真验证
为了验证文中提出的极限速度模型的有效性,利用ANSYS/LS-DYNA计算了两种锥头钨射弹侵彻不同厚度硬铝靶板的过程。数值模拟中,射弹1和射弹2直径均为d=2a=30mm,柱状部分均为50mm,其中射弹1锥角r=28.1°,射弹2锥角r=41.1°。图3为射弹1侵彻硬铝靶板等效应力云图。通过数值仿真模拟得到了四种不同弹靶工况的弹道极限速度,并与由本文建立的弹道极限模型所得结果进行了对比,如表2所示。

图3 侵彻贯穿模型图
从表2可以看出,理论公式计算结果与数值计算结果基本一致,其中理论计算结果偏小,这主要是因为射弹侵彻贯穿靶板时,射弹损失的动能除了靶板塑性变形耗能(包括局部耗能和整体耗能)外,还应包括射弹变形所消耗的能量、靶板所获的动能、热效应及波动效应所消耗能量等,而在本文中忽略了这些次要耗能机制的影响。由表2还可看出,理论计算解与数值模拟解在工程实用允许的范围内,文中建立的弹道极限速度模型是可行的。

表2 数值计算结果与理论公式结果比较
3 结语
基于准静态柱形空穴膨胀理论、量纲分析和相似原理,通过理论分析研究了射弹侵彻贯穿金属薄板的过程,给出了一个考虑靶板局部变形和整体变形的弹道极限计算公式。模型预测与数值模拟进行了比较,发现靶板弹道极限的理论预测值与数值模拟解吻合地较好。
[1] Corbett G G, Reid S R, Johnson W. Impact loading of plates and shells by free-flying projectiles[J]. International Journal of Impact Engineering,1996,18:144-230.
[2] Hill R. The Mathematical Theory of Plasticity[M]. New York: Oxford University Press,1950:125-127.
[3] 孙炜海,文鹤鸣.锥头射弹低速撞击下薄金属靶板的穿透[J].固体力学学报,2009,30(4):361-367.
[4] Borvik T, Hopperstad O S, Berstad T. Perforation of 12mm thick steel plates by 20mm diameter projectiles with flat, hemispherical and conical noses[J]. International Journal of Impact Engineering,2002,27(1):37-64.
[5] Rosenberg Z, Dekel E. Revisiting the perforation of ductile plates by sharp-nosed rigid projectiles[J]. International Journal of Solids and Structures,2010,47:3022-3033.
[6] 隋树元,王树山.终点效应学[M].北京:国防工业出版社,2000:125-128.
[7] Cupta N K, Ansari R, Gupta S K. Normal impact of ogive nosed projectiles on thin plates[J]. Int J Impact Engng,2001,25:641-660.
[8] Calder C A, Goldsmith W. Plastic deformation and perforation of thin plates resulting from projectile impact[J]. Int J Solids Structures,1971,7:863-881.
[9] Radin J, Goldsmith W. Normal projectile penetration and perforation of layered targets[J]. Int J Impact Engng,1988,7:229-259.
[10] Landkof B, Goldsmith W. Petalling of thin, metallic plates during penetration by cylindro-conical projectiles[J]. Int J Solids Structures,1985,21:245-266.
[11] Goldsmith W, Finnegan S A. Normal and oblique impact of Cylindro-conical and cylindrical projectiles on metallic plates[J]. Int J Impact Engng,1986,4:83-105.
Ballistic Limit of Thin Metallic Plates Struck by Conical-nosed Projectiles
YAN Ping1KANG De2
(1. Naval University of Engineering, Wuhan 430033)(2. No. 92207 Troops of PLA, Shijiazhuang 050300)
In this paper, the total amount of energy dissipated by targets is divided into two parts, including the energy dissipated local piercing and the energy absorbed by global deformation. Based on cavity-expansion theory, formulas of perforation deceleration for conical-nosed projectiles is derived, then the first part energy is obtained. The second part energy is derived from fitting of ballistic test data according to references with dimension analysis method and similitude rule. On the basis of these analysis, a new formula to predict the ballistic limit of thin metallic plates struck by conical-nosed projectiles is proposed. Finally, the results of theoretical formulas and numerical simulation are compared and analyzed.
conical-nosed projectiles, penetration/perforation, thin metallic plate, ballistic limit
2014年9月11日,
2014年10月29日
严平,男,博士,研究方向:弹药设计理论与毁伤学。康德,男,硕士研究生,研究方向:动能毁伤仿真。
TU511
10.3969/j.issn1672-9730.2015.03.042

