制材业原木生产计划下料问题分析
王 巍,柯育军
(东北林业大学工程技术学院,哈尔滨150040)
木材是人们日常生活中不可缺少的天然材料,我国天然森林资源比较贫乏,如何保护现有森林资源,充分挖掘资源潜力是缓解日趋紧张的木材供需矛盾的根本途径[1-3],其中,加强技术改造、提高原木和板材加工的利用率是一条主要途径。我国制材工业落后,原木的综合出材率一直很低,大部分原木都需要经过锯割加工后才能使用,如何提高原木出材率和原木利用率,对推进制材技术的现代化有着极为重要的影响[4-7]。对木材加工性能的深入研究,对充分认识和开发实体木材的利用潜能,提高木材的利用水平和实现木材工业的可持续发展具有重要意义[8-11]。
1 原木下料问题模型构建
1.1 问题描述
本文是以制材业中的木门制造企业为对象研究原木下料问题,木门制造企业统一购进只有一种规格的原木,其固定长度为7.4 m。现在需要根据客户的要求,对其进行切割,以便制成不同规格的木门,如果需要20根2.9 m长、40根2.1 m长和80根1.5 m长的该种特质原木,则应当如何对原木进行切割才能用料最省。
1.2 整数规划方法
整数规划是指一类要求问题中的全部或一部分变量为整数的数学规划。是近三十年来发展起来的、规划论的一个分支[2]。整数规划问题是要求决策变量取整数值的线性规划或非线性规划问题。
非线性的整数规划一般可分成线性部分和整数部分,因此常常把整数规划作为线性规划的特殊部分。在线性规划问题中,有些最优解可能是分数或小数,但对于某些具体问题,常要求解答必须是整数。例如:所求解是机器的台数、工作的人数或装货的车数等。为了满足整数的要求,初看起来似乎只要把己得的非整数解舍入化整就可以了。实际上化整后的数不见得是可行解和最优解,所以应该有特殊的方法来求解整数规划。
整数规划问题根据对设计变量的取值要求的不同可以分为如下几类:
整数线性规划数学模型的一般形式如下:

1.3 问题分析并建模
合理下料问题的关键在于确定合适的切割方案,在这个过程中,需要找到所有可行的切割方案,需要收集尽可能多的切割方案以考虑更多的情况。在此需要指出,切割模式必须合理,尽可能最大限度使用原材料,即余料应当小于要求的最小规格尺寸,否则原料则可以继续被切割满足需要。根据下料要求,通过试算的方法进行分析比较,得出以下8种方案。
对于上述问题,可以得到所有合理可行的切割方案,见表1。

表1 原木切割模式Tab.1 Wood cutting mode
接下来是确定设计目标,所谓的用料最省,可以有两种理解:
(1)所用的原木数量最少,这种情况适用于余料废弃。
(2)余料最少,这种情况余料可以再利用。
在这两种前提下的目标函数不同,解也可能不同。
根据上述两种理解,下面分别对其进行分析:
第(1)种理解:
假设用第i种方案切割的原木根数为Xi(i=1,2,……,8),则所需要的原木数量为切割的原木数总和,即:
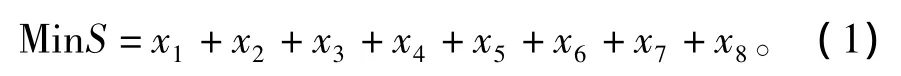
根据表格中的数据和上述假设,可以知道经过切割以后获得符合要求的各种规格的原木数目如下,设用Pi表示i米长的原木的数量,即:

由于需要20根2.9 m长、40根2.1 m长、80根1.5 m长的原木,故最后得到的各种规格的原木数目应当不小于当初定下的要求,即需要满足:

结合式(3)可得约束条件为:
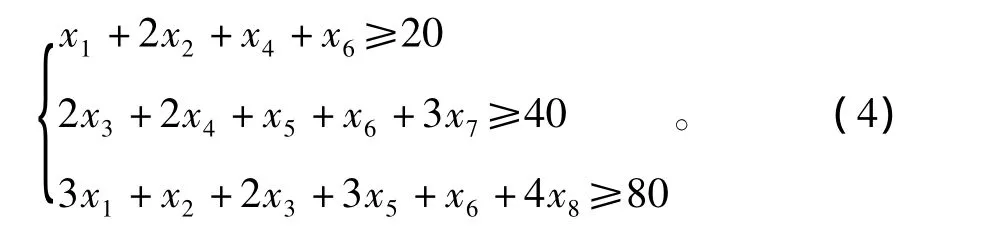
由于原木的数量是非负整数,故所采用的切割方案的各设计变量也均为非负整数。对于该问题的目标,对应的整数规划的数学模型P1为:
P1:目标函数为(1)
约束条件如公式(4):
xi≥0且取整数值。
第(2)种理解:
假设切割后所剩余的总长度W为:

同理,对于该问题的目标,对应的整数规划的数学模型P2为:
P2:目标函数为(5)
约束条件见公式(4):
xi≥0且取整数值。
2 余料废弃情况下的计算结果分析
2.1 余料废弃情况下运用LINGO软件求解
求解P1。运用LINGO算法进行求解,得到最优解的结果如下。

目标函数值
根据运行结果可知,下料结果见表2。

表2 余料废弃情况下原木切割方案Tab.2 The cutting stock problem without considering the surplus timber
即按照方案1切割17根原木,按照方案3切割5根原木,按照方案4切割12根原木,按照方案6切割6根原木,按照方案8切割10根原木,总共50根原木,总余料量24 m。
2.2 余料废弃情况下运用MATLAB软件求解
用intprog函数对P1进行求解的MATLAB代码和运行结果如下:
%目标函数所对应的设计变量的系数:
c=ones(1,8)。
%不等式约束:
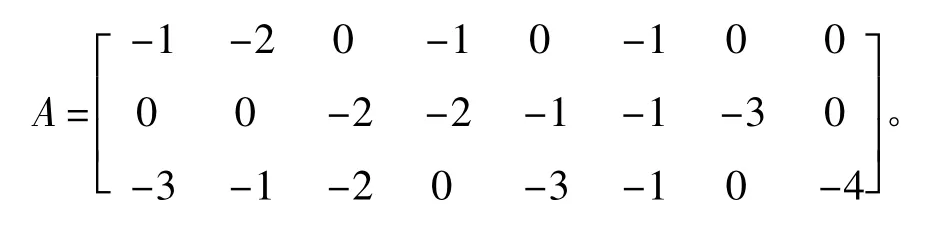
1b= [-20;-40;-80]。
%设计变量的边界约束:
1b=zeros(1,8)。
%所有变量均为整数变量,故将所有序号组成向量M:
M= [1;2;3;4;5;6;7;8]。
%判定为整数的误差限:
Tol=1e-8。
%求最优解x和目标函数值fval,并返回状态指示:
[x,fval] =intprog(c,A,b, [], [],1b,[],M,Tol)。
%求出此时的余料长度:
l= [0 0.1 0.2 0.3 0.8 0.9 1.1 1.4]*x
%最优解向量:
x=[5,5,5,0,0,10,10,10]
%在最优解处的目标函数值:
fval=
45.000 0‰。
l=
45‰。
根据上述结果可以知道,所需原木的最少数目为45根,其中采用各个方案切割原木的数目如最优解向量中的各分量值,此时的余料为35.5 m。

表3 余料废弃情况下时两种方案对比Tab.3 Comparison of the two cutting methods without considering the surplus timber
通过表3可知,原来的方法和现在的方法比较可得:在该种理解情况下,余料不可用作他用,运用LINGO算法得出需要原木50根,而通过MATLAB算法得出需要原木45根,因此能够作出改进。
3 余料再利用情况下的计算结果分析
3.1 余料再利用情况下运用LINGO软件求解
求解P2。运用LINGO算法进行求解,得到最优解的结果如下:

可选择变量值
根据运行结果可知,下料结果见表4。

表4 余料再利用情况下原木切割方案Tab.4 The cutting stock problem while utilizing the surplus timber
即按照方案1切割5根原木,按照方案2切割5根原木,按照方案4切割10根原木,按照方案5切割10根原木,按照方案6切割14根原木,按照方案8切割4根原木,总共48根原木,总余料量29.9 m。
3.2 余料再利用情况下运用MATLAB软件求解
用intprog函数对P2进行求解的MATLAB代码和运行结果如下:
%目标函数所对应的设计变量的系数:
c= [0;0.1;0.2;0.3;0.8;0.9;1.1;1.4]。
%不等式约束:
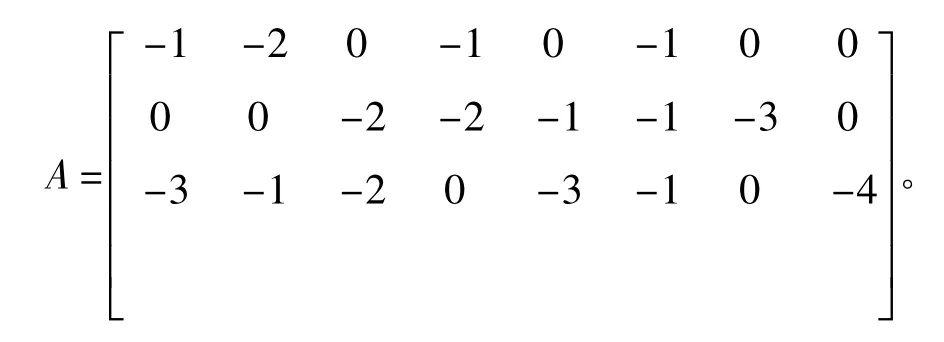
b= [-20;-40;-80]。
%设计变量的边界约束:
1b=zeros(1,8)。
%所有变量均为整数变量,故将所有序号组成向量M:
M= [1;2;3;4;5;6;7;8]。
%判定为整数的误差限:
Tol=1e-8。
%求最优解x和目标函数值fval,并返回状态指示:
[x,fval] =intprog(c,A,b, [], [],1b,[],M,Tol)。
%求出此时所需原木的数目:
s=sum(x)
x=[5,5,5,0,0,10,10,10]
fval=
45.000‰。
%原木数量:
s=
45‰。
根据上述结果可以知道,采用各个方案切割原木的数目最优解向量x中的各分量值,此时所用原木的数目为45根,余料为35.5 m。

表5 余料再利用情况下两种方案对比Tab.5 Comparison of the two cutting methods with the surplus timber reused
通过表5可知,原来的方法和现在的方法比较可得:在该种理解情况下,余料可用作别的用途,运用LINGO算法得出需要原木48根,总余料量为29.9 m,而通过MATLAB算法得出需要原木45根,总余料量为35.5 m,因此能够作出改进。
4 结束语
通过以上分析,可以得出如下结论:
(1)第一种是余料废弃情况下,如果运用LINGO算法,最终算出总共需要消耗原木50根,余料总和为24 m,而通过MATLAB算法算出总共需要消耗原木45根,余料总和为35.5 m,由于余料废弃,可以看出运用MATLAB得出的结果消耗的原木数量较少,在制材业中对原木利用率较高,因此能够得到改进。
(2)第二种是余料再利用情况下,如果运用LINGO算法,最终算出总共需要消耗原木48根,余料总和为29.9 m,而通过MATLAB算法算出总共需要消耗原木45根,余料总和为35.5 m,由于余料能够再利用,可以看出运用MATLAB得出的结果消耗的原木数量较少,而且余料量也较多,在制材业中对原木利用率较高,因此能改进实际的下料问题。
(3)通过MATLAB和LINGO的计算比较可以看出,在制材业中,运用MATLAB算法都比运用LINGO算法更优,对于提高原木的利用率都有显著的效果。
[1]袁忠良.下料优化方法与程序[M].天津:天津大学出版社,1989.
[2]王敏娜.通过整数规划来优化半导体企业的主生产计划[J].商场现代化,2010,60(17):32-33.
[3]田 园,宋维明,程宝栋.中国木材市场供给结构分析[J],森林工程,2005,21(5):20-23.
[4]唐加冕,周京徽.线性规划问题在经济生活中的应用[J].商业时代,2011,8(76):54-56.
[5] Chen-Ritzo C,Ervolina T,Terry P.Harrison T P,et al.Sales and operations planning in systems with order configuration uncertainty[J].European Journal of Operational Research,2010,3(205):604-614.
[6] Wang R C,Fang H H.Aggregate production planning with multiple objectives in a fuzzy environment[J].European Journal of Operational Research,2001,133(3):521-536.
[7]胡 明,黄 营.基于动态规划的生产计划优化模型研究与应用[J].现代计算机,2009,48(6):91-112.
[8]王 睿.生产计划的数学模型[J].平顶山学院学报,2007,22(5):67-68.
[9]曲中宪,武文华,宋代清.生产计划优化模型的研究[J].武汉理工大学学报,2008,30(8):185-188.
[10]张 鹏,夏 蓓.线性规划在生产计划制定中的应用[J].信息技术,2010,3(8):102-103.
[11]钟晓玉,董希斌.我国森林资源生态效益补偿机制的探讨[J],森林工程,2008,24(1):18-21.

