基于层次分析与可拓理论的水土流失严重程度分区评价

李雄峰，余宏明，李 亚，师华鹏

（中国地质大学 工程学院，武汉430074）

水土流失是自然界物质、能量迁移的一种过程，是指地表土层受流水作用造成水和土的流失。水土流失是降雨对地表的侵蚀作用造成的，是自然因素和人为因素共同作用的结果［1］。矿山边坡的水土流失是水土流失过程中非常重要且常被忽视的部分，矿山边坡水土流失机理涉及的领域很广，与岩—土—水—植被作用机理有着内在的关联性。水土流失灾害的严重程度通常被忽略，强烈侵蚀地区与轻微侵蚀地区采取的水土保持措施与防治工程存在着较大差异，区分不同地区水土流失危害级别可以对工程经济与确定灾害危害程度提供较大帮助，对该地区水土保持工作的开展与水土流失的评价提供有益的参考。

对于可拓学在地质灾害方面的研究始于20世纪90年代末，可拓学［2］作为一种不确定性方法于1983年创立［3］。可拓理论以不相容问题作为研究对象来研究其转化规律及解决方法。它在构造判断矩阵时，考虑将主观判断的模糊性，并采用隶属于（一∞，＋∞）的关联函数使评价更加精细化和定量化［4］。可拓学自创立以来，在地质灾害学科中应用广泛，研究成果也有很多：原国红等［5］将可拓学与岩体质量分级联系在一起，得到了岩体质量的可拓分级，能较好解决工程中的实际问题。林登科等［6］将可拓理论应用于煤矿水害安全评价中，在克服主观见解的同时得到了煤矿水害的安全等级。刘厚成等［7］将可拓理论引入了泥石流危险性评价中，对美姑河流域牛牛坝公路泥石流沟进行了评价。时惠黎等［8］在隧道塌方概率计算中也引入了可拓学理论，并得到了隧道塌方发生的概率等级。可见，可拓学在地质灾害评估与分级中具有简便、高效的优点。本文使用可拓学与层次分析相结合的方法应用于矿山边坡水土流失严重程度分区评价，试图从一个全新的角度探求水土流失严重程度分区的方法，为水土流失危险性分区研究提供一条新的分析思路，并为研究区的水土流失评估与防治提供借鉴。

1 可拓学基本原理

1.1 隶属度函数

20世纪60年代美国水土保持学家Wischmeier等提出了通用土壤流失方程式（USLE），得到了定量研究土壤侵蚀问题的有效方法［9］，在该方法基础上也出现了很多修正方程。上述方程中各因子含有不同的单位量纲，无法进行统计归纳，故需建立一个消除量纲影响的无量纲函数，该函数就是影响因子的隶属度函数［10］。应根据各个指标的性质来确定其隶属度函数的表达形式。然而，在确定隶属度时，一般要综合大量专家群体的判定结果［11］，来减小个人出现的片面性影响，但是仍然会出现一些不可避免的主观因素的影响。本文采取线性无量纲法来计算定量指标间的量纲化问题。（0，1）间的数值表示该影响因子的隶属度，本文采取边坡坡度、植被覆盖率、降雨强度、土壤性质、土壤侵蚀模数、覆土厚度、渗透性7个因子作为评价边坡水土流失严重程度的评价指标。各影响因子的隶属度公式如下：

（1）效益型

边坡坡度、降雨强度、渗透性、土壤侵蚀模数四个因子属于效益型指标，即单因子条件下数值越大水土流失产生量越大。

（2）成本型

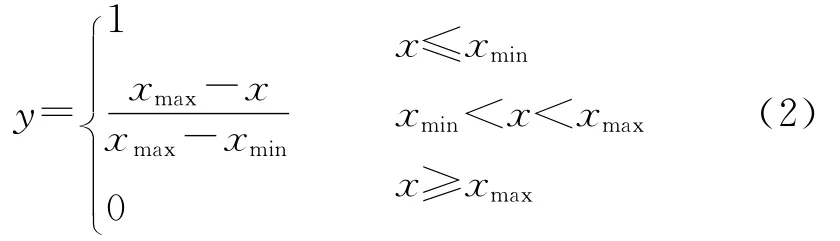
植被覆盖率、土壤性质、覆土厚度三个因子属于成本型指标，即单因子条件下数值越小水土流失产生量越大。其中：y——各因子隶属度；x——含有量纲的各因子数值；xmin——含有量纲各因子最小值；xmax——含有量纲各因子最大值。

1.2 经典域［12－13］

假定研究区内有s个边坡需做出水土流失的危害级别，即土壤侵蚀强度分级，影响因子有i个，相应分级可用一个n维物元来表述：

式中：Rs——物元；Ns——第s个评价类别；Cs——第s个评价指标；Xs——Cs所规定的量值范围，即经典域。

1.3 节 域

由集合P和它的n个特征Ci以及将标准量值范围加以拓宽的量值范围组成的物元称为节域物元，可表示为：

1.4 待评价物元

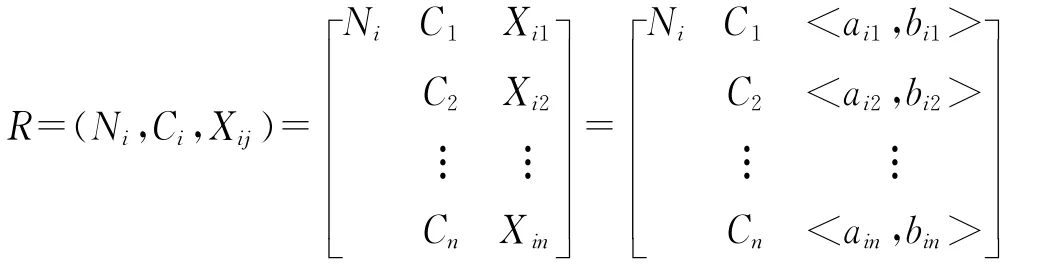
式中：Ni——第i待评边坡；——第i待评边坡的Ci值。

1.5 确定关联函数值［14－15］与关联度

待评价边坡（i）水土流失严重程度（s）与各影响因子（j）的关联度函数可按下式进行计算：

式中：j＊——待评物元Ni的级别特征值，j＊数值的大小可以判断待评物元偏向相邻级别的程度。

2 影响因子分析与评价指标的选取

本文以河南省焦作市不同地区的水土流失影响因子作为研究对象，在分析研究区各影响因子的基础上，建立水土流失严重程度分区评价模型。

2.1 矿山边坡形态是影响水土流失的主导因素

矿山边坡形态包括坡面平整程度，坡脚、坡面地质特征，边坡表面形态，坡度，坡长等。坡角是植物的适宜性及产生的水土流失决定性因素。对于不同坡度的边坡而言，坡度越缓，边坡的稳定系数越大。边坡坡面覆土的土壤侵蚀量随边坡坡度的增大而增大，水土流失量越大。坡度对坡面水土流失的影响一方面是由于坡度的增大，土壤颗粒固有重力将更有利于溅散土粒向下坡运动，土壤抗蚀能力减弱；另一方面还表现在因入渗量与坡度成反比关系，坡度大时容易产生径流，增加了溅蚀与坡面径流联合侵蚀的作用，加剧了坡面水土流失。

2.2 植被是防止水土流失的关键因素

植物防护就是现今所推广的坡面生态防护方式，利用植物的茎叶阻挡抑制雨水对坡面的冲刷，利用根系与岩土体的耦合作用来减轻坡面的不稳定性和土壤侵蚀。植被具有截流降水、涵养水源、固持土体等作用。土体和植物根系组成一个复合体，植物根系相当于土体中的加筋，提高土体的强度，增大了土壤中的附加粘聚力，增强土体的稳定性与抗剪强度。

2.3 降雨是主要的诱发因素

降雨量是影响水土流失的主导诱发因素，尤其是在坡面土体少，边坡坡度大，土壤黏粒含量高的边坡，水土流失量最大。水土流失量的大小体现则在降水时坡面径流对坡面的侵蚀量上。降雨量在一定范围内时，降雨量越大、降雨历时越短，则雨强越大，产生的坡面径流量和径流深度越大，水土流失越严重。

2.4 土壤性质是影响矿山边坡水土流失的主要因素

土壤性质的影响则表现在土壤的颗粒级配上，当细颗粒含量较高时，坡面径流越容易带走土壤颗粒，水土流失就更严重。边坡土壤的各种物理化学性质影响着土壤的易蚀程度，研究区覆土试验结果表明，该区细颗粒含量较高，这与研究区上覆黏土岩有关，风化后所得黏粒较多，发生水土流失的风险较高。颗粒小且密度较低的土壤易于被坡面径流带走而产生侵蚀。根据上述影响因子的分析，并综合考虑评价指标应符合具有明确的物理意义和代表性、各指标相互独立、容易获取和量化的原则。本文采取边坡坡度、植被覆盖率、降雨强度、土壤性质、土壤侵蚀模数、覆土厚度、渗透性7个因子作为评价边坡水土流失严重程度的评价指标。

3 边坡水土流严重程度分区评价模型的建立

3.1 评价等级隶属度的计算

根据上述影响因子的可拓隶属度分级表，结合德菲尔法与国内外相关研究进行水土流失严重程度分区评级，制定可拓分级标准（表1）与边坡水土流失严重程度评价指标等级表 （表2）。

表1 水土流失严重程度可拓分级标准（无量纲）

3.2 确定物元与待评价物元

根据表1所示所得水土流失严重程度分级标准，展开经典域可得物元如下所示：

3.3 确定经典域和节域

由上述可拓分级表与边坡水土流失严重程度评价指标等级表可确定Ⅰ—Ⅴ（1—5）级的水土流失严重程度评价等级的经典同征物元与节域同征物元如下所示：

经典域物元：

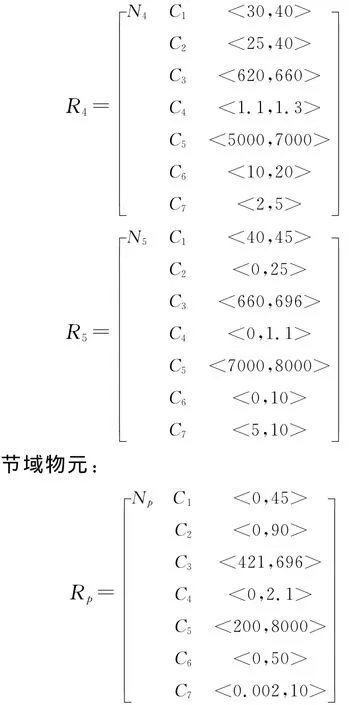
3.4 层次分析法确定影响因子权重

AHP层次分析法是一种定性与定量相结合的决策分析方法，是一种决策分析者对复杂系统的决策思维过程模型化、数量化的过程，是将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。决策者可通过将复杂的问题分解为若干层次和若干因素，在因素间进行简单的比较和计算，从而得出不同方案的权重［16］，为最佳方案的选择提供依据［17］。用Delphi法两两对比打分，计算层次排序结果。通过对水土流失评价因子分析，采用1～9标度法得到各影响因素重要性等级判断矩阵及计算权重。AHP法对上述7个影响因子反复比较并根据权重法确定水土流失评价因子比较矩阵（表3）和计算结果如表4所示。

表2 边坡水土流失严重程度评价指标等级

表3 AHP法水土流失评价因子比较判矩阵

表4 各影响因子权重计算结果

3.5 确定水土流失严重程度

焦作市各地区水土流失因子实测指标（均值）及隶属度如表5所示。

根据上述分析计算结果并根据实际考察结果。该地区水土流失危害级别为

经计算可得CI＝0.1298，CR＝0.0983＜0.1通过一致性检验，λmax＝7.7789。

将该地区的水土保持数据带入上述式（3），（4），根据评定原则，焦作不同地区的水土流失待评物元按式（9），（10）得到焦作市各地区水土流失评价等级如表6所示。

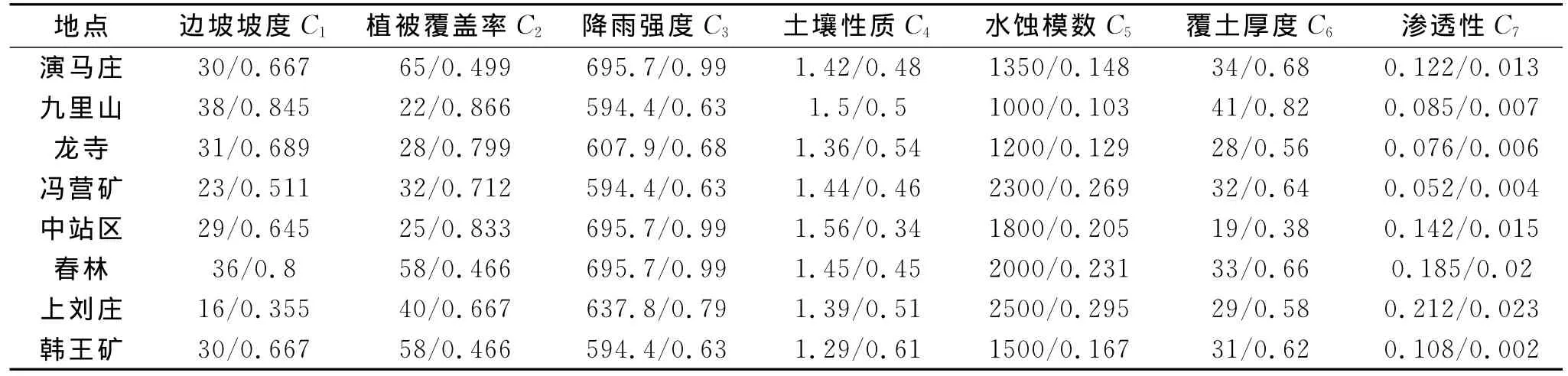
表5 焦作市各地区水土流失因子实测指标（均值）及隶属度

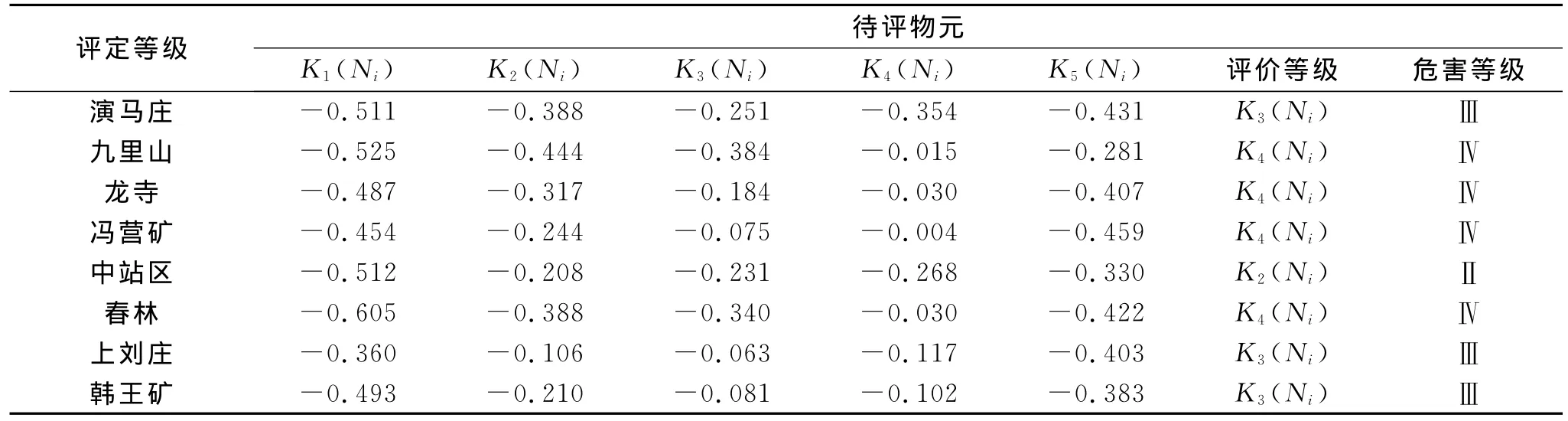
表6 关联度计算结果

根据水利部土壤侵蚀强度分级标准［18］（表7）以及该地区水保站资料，对该地区侵蚀模数与实际工程地质条件得到各地区的水土流失危害等级如表8所示。

表7 水利部土壤侵蚀强度分级标准

以上结果表明，焦作市各地区水土流失严重程度分区为：中站区为轻度侵蚀；演马庄、上刘庄、韩王矿为中度侵蚀；九里山、龙寺、冯营矿、春林为强烈侵蚀。在强烈侵蚀地段需加强水土保持措施。

4 结 论

（1）水利部土壤侵蚀强度分级结果与本文分级方法所得结果一致，说明基于层次分析的可拓评判方法运用于水土流失的严重程度分区评价是合理可行的，能够较好地反映各因素对该地区边坡水土流失问题的影响程度并且判别其危害等级，并采取及时有效的防治措施进行治理防护。

表8 焦作地区水土流失侵蚀模数分级

（2）针对焦作市不同地区水土流失因子实测指标的可拓学分析，建立了物元模型，对不同地区水土流失的严重程度分级进行了可拓学评价，实际结果与评价结果相同。

（3）该方法理论上比较严谨，且计算十分简单，具有较好的实用性。由于中站区近几年水土保持工作与环境改造工程进行较好，故其分区指数较小，与本文所得结果一致。

（4）本文将可拓学和层次分析法有机结合的可拓层次分析法（EAHP）首次应用到水土流失的严重程度分区评价上，为水土流失危险性分区研究提供了一条新的分析思路。

（5）应用可拓层次分析法（EAHP）对水土流失严重程度分区的评价进行研究具有直观的表达方式，解决了一些评价指标体系中定性问题在定量化过程中主观判断的模糊问题，这是可拓学的优点所在，但是局限于各地区定点与考察的不精确性，仍会产生误差。

［1］ 罗细芳，姚小华.水土流失机理与模型研究进展［J］.江西农业大学学报，2004，26（5）：813－817.

［2］ Cai Wen.The extension set and non－compatible problem［C］.Advances Mathematics and Mechanics in China.Beijing ：International Academic Publishers，1990.

［3］ Cai Wen.Extension engineering and applications［J］.International Journal of Operations and Quantitative Management，1999，5（1）：59－72.

［4］ 蔡文.可拓论及其应用［J］.科学通报，2004，44（7）：673－681.

［5］ 原国红，陈剑平，马琳.可拓评判方法在岩体质量分类中的应用［J］.岩石力学与工程学报，2005，24（9）：1539－1544.

［6］ 林登科，沈斐敏，廖素娟.基于可拓理论与区间赋权的煤矿水害安全评价［J］.安全与环境工程，2015，22（2）：124－128.

［7］ 刘厚成，谷秀芝.基于可拓层次分析法的泥石流危险性评价研究［J］.中国地质灾害与防治学报，2010，21（3）：61－66.

［8］ 时惠黎，马淑芝，贾洪彪.基于可拓综合评价模型的隧道塌方概率计算方法［J］.安全与环境工程，2015，22（2）：154－158.

［9］ 王倩，艾应伟，裴娟，等.遂渝铁路边坡草本植物多样性季节动态和空间分布特征［J］.生态学报，2010，30（24）：6892－6900.

［10］ 谢季坚，刘承平.模糊数学方法及其应用［M］.武汉：华中科技大学出版社，2013.

［11］ 熊怡，张家桢.中国水文区划［M］.北京：科学出版社，1995.

［12］ 蔡文，杨春燕，林伟初.可拓工程方法［M］.北京：科学出版社，2000.

［13］ 杨春燕，蔡文.可拓工程［M］.北京：科学出版社，2007.

［14］ 李桥兴，杨春燕.可拓集无量纲一维关联函数［J］.系统工程2014，32（11）：154－158.

［15］ 杨春燕，蔡文.可拓集合中关联函数的研究进展［J］.广东工业大学学报2012，29（2）：7－14.

［16］ 郭开仲.关联函数的形式［J］.智囊与物元分析，1985（1）：48－55.

［17］ 梁嘉骅，张志耀，阎骏，等.环境管理系统工程［M］.北京：北京科学技术出版社，1992.

［18］ 中华人民共和国水利部.土壤侵蚀分类分级标准［Z］.1997－02－13.