弹箭星用电爆阀可靠性验证及评估

黄清伟，袁洪滨，李 海

（西安航天动力研究所，陕西西安710100）

0 引言

电爆阀广泛用于各类导弹、火箭和卫星中，用以实现控制工作介质的通断。电爆阀的可靠性对于飞行的成败及航天员的安全性至关重要，因而合理确定可靠性验证试验方法，对在定型阶段和批生产阶段电爆阀的研制具有十分重要的意义。

电爆阀为一次动作阀门，属于成败型。目前，国内没有统一的标准来评估电爆阀可靠性。如果采用传统的成败型方法对电爆阀的可靠性进行评估，制定可靠性验证方案，需进行大量的抽样电爆试验，花费大量研制时间和巨额的研制经费。由于没有考虑到电爆阀的作动特点，所以评估结果比较保守，而且反映不出电爆阀的性能指标。航天系统内主要以少量的拉偏电爆管装药量来定性考核，无法定量给出可靠性指标，同时也不能真实反映电爆管输出爆压变化。法国、美国及俄罗斯等国采用了一种所需试验次数极少的可靠性评定方法，即：加严试验考核方法[1-2]。2002年邵德生提出了基于裕度思想的火工装置的可靠性设计方法，以及减少试验样本的强化试验验证可靠性方法[3]。上述评估方法未考虑电爆阀的产品特点，具有一定的局限性。

本文从电爆阀的力学特点出发，提出了一种评估电爆阀可靠性和试验验证的新思路，所提出的方法同样适用于成败型产品的可靠性评定。

1 电爆阀结构原理

典型的电爆阀工作原理如图1所示，通常由电爆管、阀体、活塞-切刀组件、接管嘴-衬套组件以及密封圈组成。工作时电爆管通电，产生高温高压燃气，推动活塞-切刀组件运动，切断接管嘴，并楔紧在阀体锥面上。

图1 电爆阀工作原理示意图Fig.1 Working principle of pyrovalve

2 可靠性模型

电爆阀的可靠性是指电爆阀在规定的时间和规定的条件下完成规定任务的能力。电爆阀可靠性可分为点火可靠性、火药爆炸产生爆压可靠性和机构可靠性3部分，三者之间是串联关系，如图2所示。

图2 电爆阀可靠性框图Fig.2 Reliability block diagram of pyrovalve

目前，点火一般采用高可靠电爆管，在置信水平为0.95时，可靠性可达到0.999 9，同时，对于机械作动结构来说，过程质量控制使其可靠性能已经比较稳定，用传统的计数和计量方法检验，即可满足可靠性要求。基于以上原因，假定：点火可靠度R1与机构动作可靠度R3均为1，这样电爆阀的可靠度RL即为火药产生爆压可靠性R2。

由以上假设，得到电爆阀可靠性等于火药爆炸产生的压力大于所需最小压力同时小于所需最大压力时的概率，即

火药爆炸产生的压力决定于火药爆炸产生的燃气压力p。由于环境温度、压强、药粒厚度及均匀性等存在一定散差，这些独立随机因素的影响造成了火药爆炸时产生的压力值并非某一确定值，而是呈正态统计分布特性[4]。这种分布特性也造成了电爆阀在某种情况下可能会出现超压的不可靠情况。同样所需的压力也是受不同的独立的随机误差影响，由中心极限定理可知其近似服从正态分布。因此，电爆阀两个参数服从正态分布，其可靠性评估模型如图3所示。

图3（a）为电爆管爆炸产生压力在电爆阀所需的压力范围内，此时电爆阀正常动作，其可靠性为1。图3（b）中阴影是电爆管爆炸产生的压力与电爆阀所需的压力有重叠部分,此时电爆阀有可能失效,阴影部分即为失效区。

由于在实际试验中电爆阀可靠动作所需压力可以通过设计、加工及装配等方式很好地控制，使其方差接近于0，此时电爆阀可靠动作所需压力可视为常值，其可靠性模型简化为如图4所示，可靠性为：

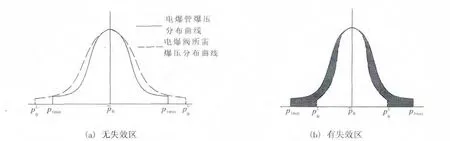
图3 电爆阀可靠性模型Fig.3 Reliability model of pyrovalve

图4 简化的可靠性模型Fig.4 Simplified reliability model

3 可靠性验证及评估原理

将产品放到恶劣的环境下，通过增大或者减小电爆阀内爆压，以降低其可靠性，用经典方法推断在额定环境下产品的可靠度。根据目前使用经验，电爆管装药量改变量与其输出爆压无法定量描述，因此采用改变电爆容腔容积模拟电爆管爆压改变。

为了利用pB的统计量评估电爆阀的可靠性，假设有如下对应关系：

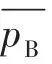
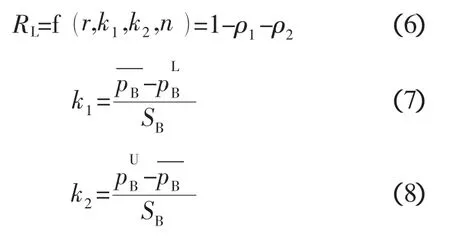
式中：ρ1和ρ2分别为标准正态分布的上侧概率和下侧概率。

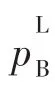
一般取 k1=k2，结合式（3）～式（8）可以设计出极限容腔，然后按照极限容腔加工产品，并根据产品使用环境进行试验。试验后按照实际试验产品极限容腔、试验台数、试验成功台数进行可靠性评估。

4 可靠性验证及评估示例

4.1 已知条件

一种火箭用电爆阀的可靠性要求及设计参数如下：

1）用户要求：置信度r=0.85时，RL≥0.99；

2）电爆管验收参数：▽B=30 cm3，p1min=7 MPa，p1max=14 MPa；

4.2 可靠性验证

1）根据 r=0.85，RL=0.99,查阅 GB/T4086.1或者QJ1384，得到n与k1，k2有如下对应关系：

n=2 5 7 9 12 20

k1=k2=16.6 5.05 4.35 4.01 3.72 3.38

取n=9，则k1=k2=4.01。

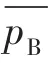
4）按照表1生产了大小极限容腔产品各9台，根据使用要求进行了力学环境试验、热环境试验、电爆试验、电爆前后漏率检查和爆破压力等，产品结构和性能均满足使用要求。

表1 极限容腔试验Tab.1 Test of limit volume

4.3 可靠性评估

3）根据 k1，k2，r，n=15，反查 GB/T4086.1或者 QJ1384 得到 ρ1=0.000 086，ρ2=0.000 01；

4）将p，p2带入式（6），得到RL=0.999 904，满足用户“置信度r=0.85时，RL≥0.99”的要求。

本方法与成败型二项分布所需试验次数对比见表2。

表2 本方法与成败型二项分布所需试验数量对比Tab.2 Quantity of test samples needed by this method and pass-fail method binomial distribution

由表2可知，在验证置信度r=0.85，可靠性RL=0.999 9时，利用成败型二项分布所需无失效样本数量为18 970台，利用本文提出方法所需无失效样本数量为30台，因此本文提出的方法具有极大的优越性。

5 结论

本文提出的电爆阀可靠性验证及评估方法，是通过改变电爆容腔的安全裕度试验方法，已经成功用于弹箭星用多种电爆阀的可靠性验证及评估。该方法可以用极少的试验次数验证极高的可靠性，尤其是当可靠性要求高时，优越性更加显著。该方法不但可以用于电爆阀，还可推广到成败型产品的可靠性验证及评估，产生巨大的经济效益。

[1]BEURTEY X.Reliability prediction on Ariane 5 pyrotechnicaldevicesusing the hardened testmethod[C]//Proceedingsof Probabilistic Safety Assessmentand Manag-ement.Crete Greece：Springer London Ltd,1997：1687-1695.

[2][苏]卓洛托夫,季托夫.空间运载器的可靠性保证[M].潘绍珍,译.北京：宇航出版社,1996.

[3]邵德生.关于火工装置的可靠性设计与验证问题[J].质量与可靠性,2002,(增刊2)：34-36.

[4]胡昌寿.航天可靠性设计手册[M].北京：机械工业出版社,1999.