基于自适应预测算法的APF无差拍控制方法

李锦彬，黄靖（福建工程学院 信息科学与工程学院，福建 福州350118）

基于自适应预测算法的APF无差拍控制方法

李锦彬，黄靖
（福建工程学院 信息科学与工程学院，福建 福州350118）

有源电力滤波器（active power filter，APF）补偿电流跟踪控制要求具有较高的稳态精度和较快的动态响应速度。文章将自适应预测滤波算法应用于无差拍控制，实现APF补偿电流精确控制。根据APF时域数学模型，推导滤波系统的无差拍控制离散方程；通过自适应（finite impulse response filter，FIR）预测滤波算法实现基波电流预测，消除控制系统的计算延迟，给无差拍控制提供所需的指令电流预测值。对预测算法进行MATLAB仿真，验证预测算法的稳态精度和动态跟踪快速性；实验室样机验证控制实验结果证明所提出的控制策略有效的，具有一定的实用性。

有源电力滤波器；自适应预测算法；无差拍控制

随着以功率开关电源为典型代表的非线性负载大量使用，电力系统的谐波污染日趋严重，使其他用电设备的工作性能下降，甚至无法运行［1－2］，因此，谐波抑制新技术成为当今的研究热点。并联型有源电力滤波器（shunt active power filter，SAPF）能动态补偿谐波电流，能适应负载的随机波动以及电工设备参数的漂移，比传统的无源滤波技术更具优越性，因此有源电力滤波器（active power filter，APF）已成为电力谐波治理的理想选择，备受青睐［3－4］。

APF补偿的精确性主要取决于电流环控制器的结构、类型及算法实现手段。理论的发展总是超前于高性能微处理器，随着数字信号处理器性能的不断提高，无差拍控制、时间序列分析的预测控制、神经网络自适应控制等复杂控制方式的实现已成为可能［5］。无差拍控制是基于数学模型的全数字化控制技术，控制的稳态精度高，而且动态响应快，得到相关科研工作者的广泛关注［5－8］。由于检测算法的计算延时给控制系统前向通道带来滞后环节，因此对指令电流的超前调节或预测精度将决定无差拍控制的效果。文献［7］提出了一种基于FIR模型的自适应预测滤波器，实现谐波电流预测，但未提及补偿电流的控制策略。文献［8］提出基于灰色理论的APF预测控制，算法非常清晰，但相对于自适应FIR预测滤波器算法来说较为复杂，由于算法中用到的乘法较多，因此计算量也非常大，若要提高灰色理论的预测精度就必须对方案进行改进，采用多（digital signal processor，DSP）系统，其中一个（DSP）专门用于预测模型拟合，增加了系统的复杂性。

针对三桥臂、两电平SAPF本文提出一种新型实用的控制策略，用滑窗迭代（decrete Fourier transform，DFT）算法提取负载基波电流，保存最新的N个样值，经FIR自适应预测算法，对基波电流进行预测，在相同采样频率下提供更为精确的谐波电流预测值，经无差拍控制模型计算出（pulse width modulation，PWM）逆变器的指令电压，由电压空间矢量脉宽调制产生PWM触发信号，控制主电路，产生补偿电流。该控制方案在实验室的SAPF样机上得到验证。

1 SAPF无差拍控制策略

1.1 SAPF的数学模型

SAPF电路结构如图1所示［5］。其中ea、eb、ec为电网电压，iLa、iLb、iLc为负载电流，ica、icb、icc为补偿电流，L为APF交流侧滤波电感，R为电感的等效电阻，C是变流器直流侧储能电容。

根据图1可回路电压方程，如式（1）

式中，uao、ubo、uco为逆变器交流侧输出电压。

由式（1）可以看出abc坐标系下三桥臂APF可以进行单独控制。以a相为例，可得APF的传递函数为

根据式（2），控制交流电压uao就可以控制逆变器的输出补偿电流ica。

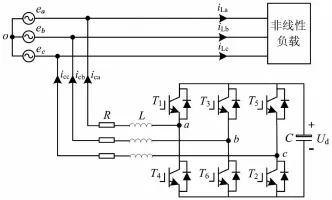
图1 SAPF电路结构图Fig.1 Power circuit diagram of SAPF

1.2 无差拍控制策略

无差拍控制的基本思想［6］：根据下一周期谐波电流预测值、当前补偿电流实际值以及当前电网电压值，根据差分方程计算出逆变电路的指令电压值，用空间矢量脉宽调制方法对指令电压进行调制，得到相应的开关模式，实现补偿误差等于零的目标。无差拍控制对给定值的响应速度快，容易数字化实现，根据微分方程式（1），离散化可得式（3）。

式中，T为开关周期，icx（k）（x＝a、b、c）为APF的当前三相补偿电流值，icx（k＋1）为下一周期的补偿电流参考值。

根据式（3）可知，影响无差拍控制精度的因素主要在以下3个方面：icx（k＋1）的预测精度；R、L等电路参的测量精度；采样周期的大小。若采用当前时刻所检测计算的负载谐波电流作为下一时刻的补偿电流参考值，实际上是差一拍的控制方案。若要实现真正意义上的无差跟踪控制，必须对补偿电流参考值进行预测。

SAPF系统包括电压外环和电流内环，系统结构图如图2所示。本文电压环采样传统的（proportion integration，PI）调节器，通过电流内环把直流侧电压稳定在参考值。电流内环的上层算法模块中，首先采用滑窗迭代DFT法检测基波电流，经自适应预测算法估计下一采样时刻的基波电流，负载电流减去基波电流预测值即得到补偿电流参考值，经式（3）无差拍计算得到逆变器电压指令值，由空间矢量脉宽调制得到三相PWM信号，触发主电路功率开关管。可见，电流预测精度是影响APF控制效果的主要因素。

图2 SAPF控制系统框图Fig.2 Block diagram of control system of SAPF

2 自适应预测算法

从信息处理的角度分析，信号预测就是对未来值进行估计，因此可以解决延时问题。鉴于基波信号的可预测性，采用自适应FIR预测滤波（least mean square，LMS）算法，预测基波信号［7］。当采样时刻到来时，由于基波电流预测值在上一时刻已经产生，因此只需用当前时刻检测到的负载电流减去对应的预测值，即可得到APF补偿电流指令值。

自适应预测算法的实质就是根据当前时刻的输入信号和一定量的输入信号的历史值，经某种运算，估计出某种频率成分的未来变化［8］。在APF中，对应的就是根据负载基波电流的最新样本来统计或估计基波分量的未来变化趋势，拟合模型，根据模型计算未来的某一时刻的基波电流值。本文的自适应预测算法结构如图3所示。

图中，if（n）是滑窗迭代DFT算法提取的当前时刻基波电流，作为预测滤波器的输出期望值。i＾f（n）和i＾f（n＋1）为基波信号预测值，e（n）为预测误差。X（n）＝［if（n），if（n－1），…，if（n－N ＋1）］T，是预测器的输入信号向量，N为数据窗的长度。

自适应FIR滤波的运算式为：

其中，HT（n）＝［h0（n），h1（n），…，hN－1（n）］为预测器的系数向量，作为滤波器数学模型参数决定着滤波器的性能，为实现自适应滤波，必须对预测滤波器的系数实时优化，从而实现自适应跟踪负载基波电流。

图3 自适应预测算法结构图Fig.3 Configuration of adaptive prediction algorithm

滤波器系数自行修正算法采用LMS算法，输入信号为e（n）和X（n），每个周期修正一次，当输入信号和噪声的统计特性发生变化时，LMS算法能够马上感知并对滤波器系数进行调整，保证输出的基波信号跟踪上负载的变化，实现自适应过程。

关于预测滤波器的系数向量HT（n）的计算，本文采用最陡梯度法的近似实现

基于LMS算法自适应预测滤波过程及滤波器系数自我修正的计算流程如下：

1）初始化上下两层自适应滤波器的系数，初值置零，并初始化收敛因子μ；

2）信号向量X（n）输入上层滤波器，根据式（4）计算出预测值i＾f（n＋1）；

3）信号向量X（n）经延迟环节z－1后进入下层滤波器，根据式（4）计算出预测值i＾f（n）；

4）根据e（n）＝if（n）－i＾f（n）计算预测误差；

5）根据H（n＋1）＝H（n）＋2μe（n）X（n）修正滤波器系数。

新的迭代周期到来时，返回第2）步。通过不断滚动优化调整滤波器系数H（n），使i＾f（n）跟踪if（n）的变化，当i＾f（n）跟踪上if（n）时，上层滤波器的输出值i＾f（n＋1）就是基波电流的预测值，为无差拍控制所需的谐波电流指令值提供可能。

3 仿真验证

基于上文理论分析，对预测算法进行仿真研究。具体参数为：三相电网电压为220V/50 Hz标准正弦波；三相不控整流器带10 Ω电阻作为非线性负载；采样频率取6.4 kHz，数据窗长度N＝128；仿真时间设为0.4 s；算法中收敛因子μ取0.007。当仿真时间为0.2 s时，负载突变为5 Ω，以此来验证检测方法的动态响应特性。仿真结果如图4所示。

图4 基于LMS算法的自适应预测仿真结果Fig.4 Simulation result of adaptive prediction using LMS algorithm

仿真结果表明：基于FIR模型的自适应预测滤波器稳态时能准确预测基波电流，动态是可以在一个电网周期内跟踪负载的突变，满足国家电网关于谐波抑制的要求。

4 实验验证

设计了基于TMS320F28335 DSP的并联型三相APF系统。直流母线电压参考值为750 V，储能电容C＝10 000 μF。实验室的非线性为相控整流器带纯电感负载，相控触发角设置45°，电感值为10 mH。实验波形如图5所示。图5（a）为APF投入补偿前已建立的直流母线电压及负载电流波形；图5（b）为稳态时APF补偿电流和补偿后电网侧的电流。可见，本文提出的无差拍控制方案中，自适应预测滤波器可以提供准确的补偿电流预测值；图5（c）为突加负载时APF系统动态跟踪实验波形，由图可知，突加负载时系统经过3个电网周期后进入稳态，动态特性满足工程要求。

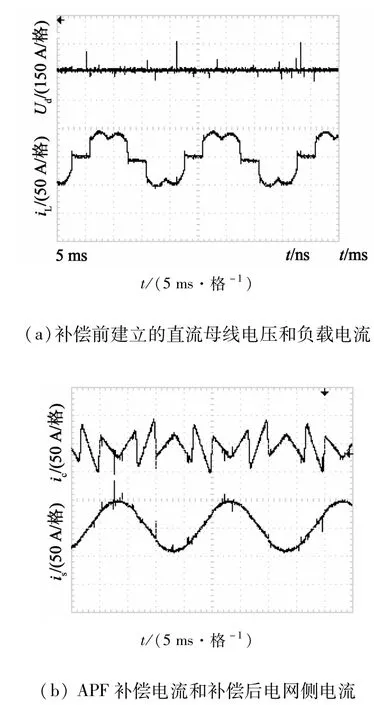
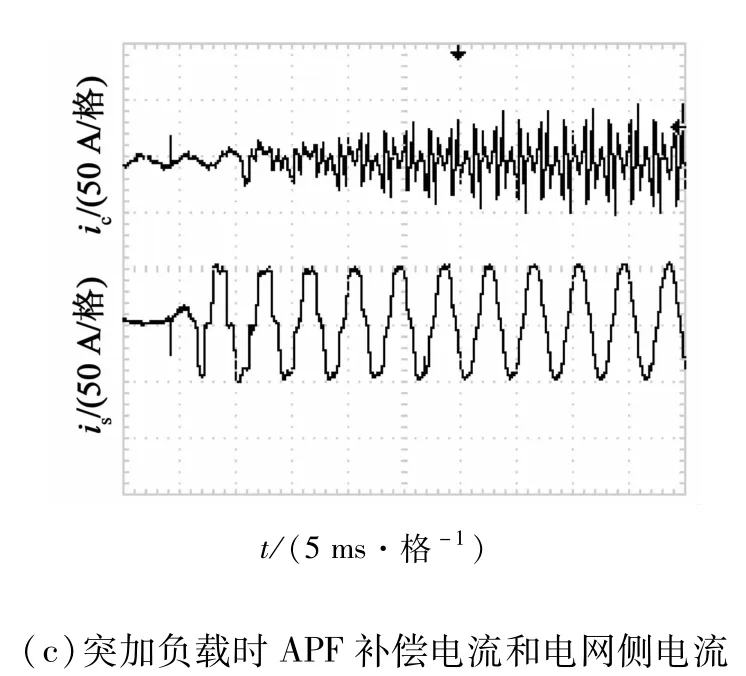
图5 实验波形Fig.5 Experimental waveforms

5 结论

有源电力滤波器的滤波效果取决于跟踪控制系统的性能，本文把基于FIR模型的自适应预测算法应用于APF无差拍控制，对其进行理论和实验研究，结论如下：

（1）影响无差拍控制跟踪效果的主要因素是补偿电流指令值的预测算法。

（2）提出的自适应预测算法可以在一个电网周期内精确预测出基波电流的未来值，实现无差拍控制，改善APF补偿效果。

（3）所提的控制策略在SAPF样机进行验证，实验结果证明了控制策略的可行性。

［1］王兆安，杨君，刘进军，等.谐波抑制和无功功率补偿［M］.北京：机械工业出版社，2005.

［2］杨君，叶杰，吴钫，等.谐波电流分次补偿控制的等效性研究［J］.电力电子技术，2015，49（5）：80－83.

［3］Liserre M，Blaabjerg F.Design and control of an LCL-filter based three phase active rectifier［J］.IEEE Transactions on Industry Applications，2005，41（5）：1281－1290.

［4］邱晓初，肖建，刘小建.一种APF模糊自适应可变环宽滞环控制器［J］.电力系统保护与控制，2012，40（7）：73－77.

［5］周娟，秦静，王子绩，等.内置重复控制器无差拍控制在有源滤波器中的应用［J］.电工技术学报，2013，28（2）：233－238.

［6］何英杰，刘进军，王兆安，等.基于重复预测原理的三电平APF无差拍控制方法［J］.电工技术学报，2010，25（2）：114－120.

［7］陆秀令，张振飞，胡红艳，等.基于自适应FIR预测滤波器的谐波检测［J］.高电压技术，2008，34（7）：1494－1498.

［8］张培远，李静.灰色预测控制在三电平4桥臂APF中的应用［J］.电气传动，2013，43（1）：44－48.

（责任编辑：肖锡湘）

A deadbeat control strategy based on self-adaptive prediction algorithm for APF

Li Jinbin，Huang Jing
（College of Information Science and Engineering，Fujian University of Technology，Fuzhou 350118，China）

The compensation current tracking control for active power filter（APF）requires high steady precision and dynamic response performance.In this paper，self-adaptive prediction algorithm was employed in deadbeat control to realize the precise control of compensation current of APF.Based on the APF time-domain mathematical model，the deadbeat control discreet equation used in the filter system was deduced.To eliminate the calculation delay of the control system to realize the beat control，a self-adaptive prediction FIR filter was introduced to realize the fundamental wave current forecast.Simulation results of the prediction algorithm verify the steady precision and speedy dynamic tracking of the prediction algorithm and the practicability and effectiveness of the proposed algorithm.

active power filter（APF）；self-adaptive prediction algorithm；deadbeat control

TM993

A

1672－4348（2015）06－0573－05

2015－11－01

福建省教育厅基金项目（JA12229，JA13228）

李锦彬（1973－），男，福建东山人，副教授，硕士，研究方向：电网谐波补偿技术。