跟踪误差投资组合鲁棒优化模型及其衍生模型在基金市场中的应用
王志强,赵 庆
(东北财经大学金融学院,辽宁大连 116025)
跟踪误差投资组合鲁棒优化模型及其衍生模型在基金市场中的应用
王志强,赵 庆
(东北财经大学金融学院,辽宁大连 116025)
基于跟踪误差投资组合鲁棒优化模型,提出三种衍生模型:单一目标收益模型、多目标收益模型和基于成本单一目标收益模型。给出了利用MATLAB求解的具体方法,采用“光大保德信均衡竞选股票基金”数据进行实证分析,并与基准模型和基金的实际投资绩效进行比较,结果表明,三种衍生模型对于提高收益、降低风险是有效的、可行的,对于资产配置具有借鉴意义。
跟踪误差;投资组合;鲁棒优化;基金市场
一、引 言
投资组合通常是指个人或机构所拥有的由股票、债券及衍生金融工具等多种有价证券构成的一个投资集合,投资组合的优化和多元化发展不仅丰富了金融投资决策的方法而且加深了对金融市场的认识。Roll[1]在Markowitz[2]均值-方差模型框架下提出跟踪误差投资组合模型,即投资组合管理者预期给定一个基准投资组合,通过跟踪误差来对投资组合管理者的投资业绩进行评价,基于跟踪误差的投资组合方法在金融界得到广泛运用。Rudolf等[3]给出了最小风险跟踪误差模型的线性模型,方便了跟踪误差模型的实践应用。王秀国和邱菀华[4]基于跟踪误差模型提出了跟踪误差多因素投资组合决策模型,并给出了数值分析。罗金川和房勇[5]提出了分层主成分分析方法,采用完全复制标的指数的投资策略来构建因素投资组合选择模型最小化跟踪误差,在此基础上通过改变分层的数量控制投资组合的跟踪误差。
但是由于金融市场波动和金融风险加剧,Black和Litterman[6]指出均值-方差模型框架下关于要求随机变量均匀分布和对期望收益和协方差的敏感性的缺陷。基于此,众多学者进行了鲁棒优化算法的研究。Costa和Paiva[7]提出了基于线性矩阵不等式的跟踪误差投资组合鲁棒优化算法。高莹和黄小原[8]同样基于线性矩阵不等式方法研究了将跟踪误差投资组合鲁棒优化在中国基金市场的运用。
本文基于跟踪误差投资组合鲁棒优化模型利用MATLAB提出新的求解算法,同时提出其衍生模型:单一目标收益跟踪误差投资组合鲁棒优化模型、多目标收益跟踪误差投资组合鲁棒优化模型和基于成本单一目标
收益跟踪误差投资组合鲁棒优化模型,并将其在中国资本市场进行了实证分析。
二、模型描述
(一)跟踪误差投资组合鲁棒优化基本模型
本文基于Costa和Paiva[7]跟踪误差投资组合鲁棒优化模型结合中国资本市场实际情况,提出投资组合收益满足预期收益要求,使得投资组合风险最小化的跟踪误差投资组合鲁棒优化模型:
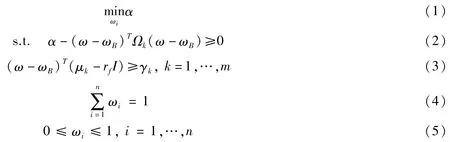
投资组合中,下标i表示投资组合中资产i;下标k表示第k种情景得到的期望收益和协方差矩阵。外生变量ωB为模型中根据预先设定目标确定的基准投资组合;γk是第k种情景下投资组合预先设定目标收益;rf是投资组合中无风险收益率。随机参数μk是由不同情景得到的期望收益;Ωk则是由相应情景预期收益的协方差矩阵。跟踪误差投资组合鲁棒优化模型中需要确定两个决策变量即内生变量ωi和α。其中ωi是投资组合中各项资产权重,α为引入的偏差波动的上界变量,,其中为跟踪误差投资组合鲁棒优化模型的方差。投资组合的目标函数是求α最小的投资组合权重ωi,数理金融含义是:在市场风险最大的情景下,选择投资组合权重ωi使得投资组合收益波动最小,即。式(3)是投资组合关于期望收益约束,I为单位列向量;式(4)是关于投资组合权重约束;式(5)表示根据资本市场实际情景不允许卖空。
(二)跟踪误差投资组合鲁棒优化衍生模型
根据Costa和Paiva[7],高莹等[8]学者的研究,跟踪误差投资组合鲁棒优化模型在资本市场具有适用性,然而面对资本市场的复杂性,本文在其基础上提出衍生模型。
1.单一目标收益跟踪误差投资组合鲁棒优化模型
假定投资组合是根据基本分析方法构建股票集,面对不同的情景集,在既定的单一收益目标约束下γ1=γ2=…=γk=γ选择投资组合具体的投资权重,即单一目标收益跟踪误差投资组合优化模型,这与Costa和Paiva[7]、高莹等[8]假设相同。
2.多目标收益跟踪误差投资组合鲁棒优化模型
许多投资组合优化模型在假设时都按照单一收益目标约束γ1=γ2=…=γk=γ下选择组合资产权重。然而在实际中,投资组合管理者针对不同市场预期采用相同的目标收益是不科学的,投资组合管理者的目标收益与市场预期是相关的,当投资组合管理者面对较乐观市场预期时会提高目标收益,面对悲观市场预期时会降低目标收益。特别是跟踪误差投资组合鲁棒优化模型在不同情景集下即在不同股票预期收益下,假定单一目标收益显然与实际情景不相符。多目标收益跟踪误差投资组合鲁棒优化模型则是在单一目标收益的基础上,根据不同市场预期制定不同的目标收益,即γk,k=1,2,…,m不全部相等提出的优化模型。
3.基于交易成本单一目标收益跟踪误差投资组合鲁棒优化模型
组合优化的目标是在风险与收益之间权衡从而选择投资组合最优权重的过程,传统上这个过程与交易成
本是分开考虑的,然而这样得到次优权重经常会导致巨大的交易成本,并且在一些情况下会严重影响经风险调整的组合收益。
基于交易成本单一目标收益跟踪误差投资组合鲁棒优化模型是在单一目标收益模型基础上引入交易成本函数:TC(ω)=(TC1(ω1),TC2(ω2),…,TCn(ωn)),i=1,…,n,其中TCi(ωi)代表第i种资产交易成本,ωi代表第i种资产权重。则投资组合净权重为:;投资组合基准权重为:;投资组合收益为:,其中μ=(μ1,μ2,…,μn)为n种资产预期收益;投资组合净收益为:;投资组合风险为:,其中Ω为投资组合中资产协方差。则基于交易成本单一目标收益跟踪误差投资组合鲁棒优化模型为:
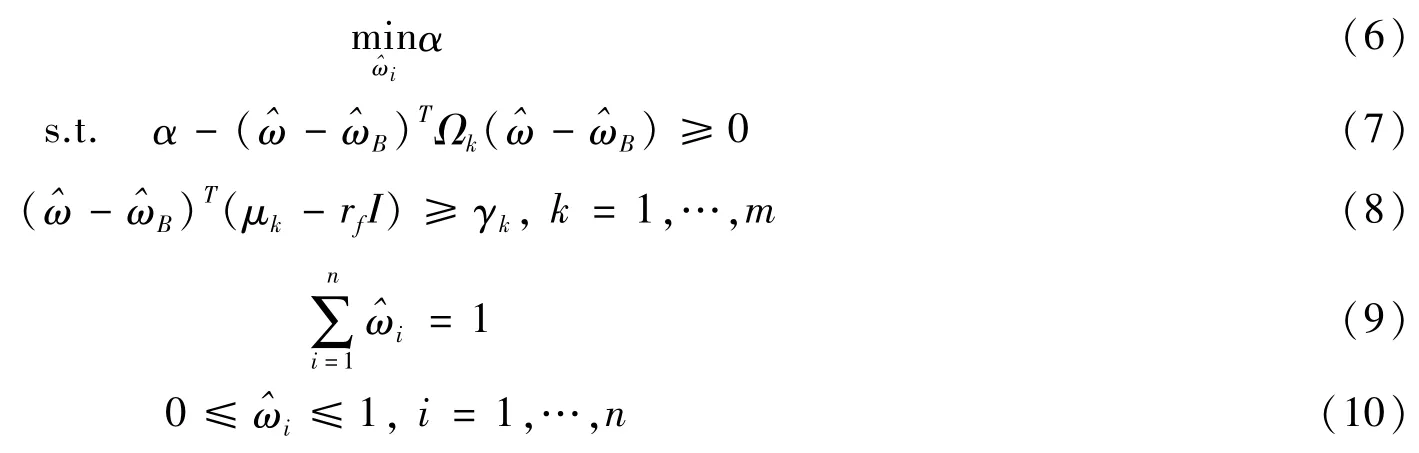
(三)MATLAB Fmincon求解非线性约束函数
Fmincon函数是MATLAB主要内置的求解非线性有约束最优化的函数,标准形式为:

三、跟踪误差投资组合鲁棒优化衍生模型在基金中的应用
(一)单一目标收益跟踪误差投资组合鲁棒优化模型转化为Fmincon函数标准形方法及在基金中的应用
以光大保德信均衡竞选股票基金(基金代码360010)的交易数据为实证数据,根据MATLAB Fmincon函数提出一种新的求解方法,并将单一目标跟踪误差投资组合鲁棒优化模型的最优解与基准组合、基金实际组合的结果进行比较。
1.实证假设
假设(1):基金360010在2013年第4季度投资组合构建是根据投资组合中各股票前6个月度收益率进行判断。
假设(2):根据我国基金管理办法每季度公布股票重仓股组成,同时根据数据可得性,假定基金360010每季度调整一次投资比例,即在持有期内2013年第4季度投资组合中各股票权重比例不变。
2.数据选取
选取光大保德信均衡竞选股票基金(360010)在2013年第4季度投资组合10支重仓股。样本数据为2013年3月至2013年9月的月度收盘价,并且将收盘价依据(Pt-Pt-1)/Pt-1转化为2013年4月至2013年9月月度收益率,数据来源于大智慧软件。
3.计算方法及计算结果
(1)基准组合权重及收益。取基准投资组合权重ωB为10×1矩阵ωB=(1/10,1/10,…,1/10)T,则基准投资组合收益率为10只股票月度收益率均值。
(2)构造情景集及组合收益和协方差。本文考虑2种计算情景集方法,即k=1,2。
情景1,期望收益μ1为10×1矩阵是依据历史数据按算术平均值计算,相应协方差矩阵Ω1为10×10矩阵。
情景2,期望收益率μ2是按由近及远0.3、0.2、0.2、0.1、0.1和0.1权重计算得到,即最近期收益的权重是0.3,以后依次类推,最远期收益率的权重是0.1,原因是距离当前较近时期的收益率对基金经理预期判断影响较大。情景2下期望收益的协方差矩阵Ω2为10×10矩阵。
(3)单一目标收益跟踪误差投资组合鲁棒优化模型Fmincon函数标准化过程。
情景1下,单一目标收益跟踪误差投资组合优化模型Fmincon函数标准化过程。为使得跟踪误差模型转化为fmincon函数标准形式,设x=(α,ω2,ω2,…,ωn)。
则式(1)转化为标准形式(11)为:

取基准投资组合权重ωB中元素ωBi=1/n。
式(2)转化为标准形式(12):
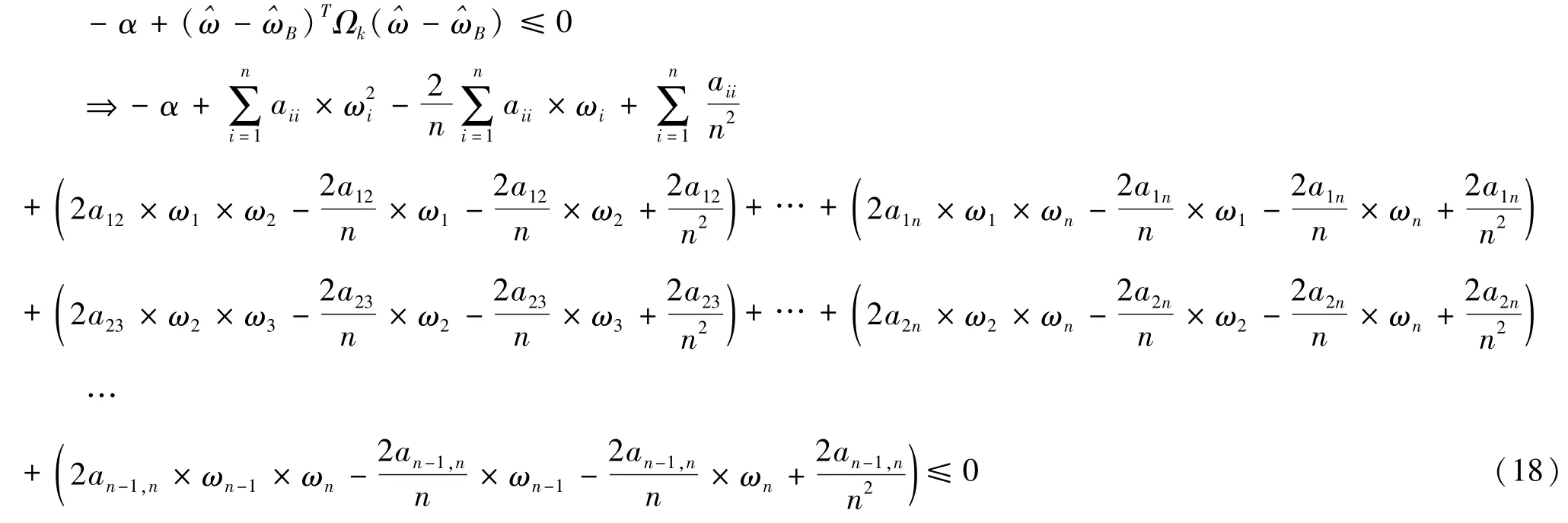
则非线性约束函数c(x)为式(18)。
将式(3)转化为标准形式(14),根据条件γ1=γ2=…=γk=γ,则A为1×11矩阵:
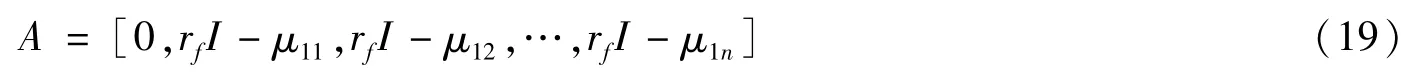
b为1×1矩阵:
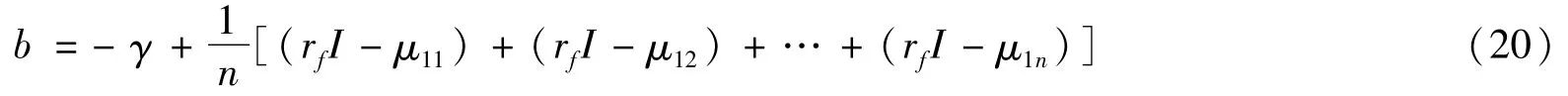
将式(4)转化为标准形式(15),则Aep为1×11矩阵:

beq为1×1矩阵:

将式(5)转化为标准形式(16),则lb、ub为11×1矩阵:

其中,inf代表正无穷。
根据偏差波动的上界变量α≥0及各资产卖空限制即ωi≥0,则Fmincon函数标准形式中初始迭代点矩阵为11×1矩阵:

综上所述,情景1下,单一目标收益跟踪误差投资组合优化模型(1)—(5)转化为Fmincon函数标准化形式式(11)—(16):式(1)转化标准形式(11)为式(17);式(2)转化标准形式(12)为式(18);式(3)转化标准形式(14)为式(19)和式(20);式(4)转化标准形式(15)为式(21)和式(22);式(5)转化标准形式(16)为式(23)和式(24),其中Fmincon函数标准形式中初始迭代点矩阵为式(25)。
单一目标收益跟踪误差投资组合优化模型情景2转化为Fmincon函数标准形式计算方法与情景1计算方法相同。由于篇幅所限情景1与情景2具体函数值未给,备索。
利用MATLAB Fmincon函数求解单一目标跟踪误差投资组合鲁棒优化模型情景1和情景2下各资产权重,其中,γ1=γ2=0.05,无风险收益率取工商银行2013年整存整取一年期存款利率,即γf=0.0325,同时为比较投资绩效也给出了基金实际各资产权重,如表1所示。

表1 单一目标跟踪误差投资组合鲁棒优化模型情景1、情景2和基金实际各资产权重
由表1可见,情景1和情景2各资产权重不相同,其原因是对于市场不同预期会影响各项资产权重。情景1下偏差波动上界变量α1=0.0008,情景2下偏差波动上界变量α2=0.0016,α2>α1,根据模型定义选择情景2下各资产权重作为单一目标收益跟踪误差投资组合优化模型最终各项资产权重。
为衡量金融资产组合的绩效表现,采用与康志林[9]相同评价方法,投资组合绩效=收益/风险。比较分析单一目标收益跟踪误差投资组合优化模型情景1、情景2、基金实际和基准收益投资绩效,如表2。
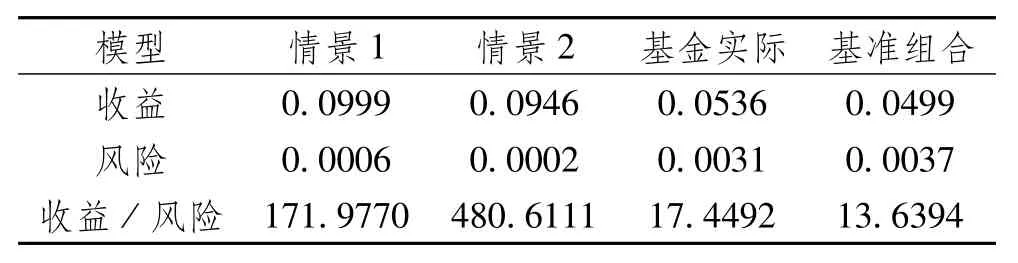
表2 各模型下投资绩效
由表2可见,从收益角度而言,单一目标收益跟踪误差投资组合优化模型情景1和情景2收益率均显著高于基金实际情景与基准模型,并且显著高于投资组合目标收益γ=0.05,表明该模型对于提高基金收益是有效的;从风险角度而言,情景1和情景2风险均显著低于基金实际情景与基准模型,表明该模型对于分散风险同样是有效的;故此,单一目标收益跟踪误差投资组合优化模型情景1和情景2投资绩效显著优于基金实际情景和基准模型,表明单一目标收益跟踪误差投资组合优化模型可以显著提升基金表现。虽然单一目标收益跟踪误差投资组合优化模型情景1模型收益率高于情景2模型,但是风险更高,并且投资绩效显著低于情景2模型,从另一个角度而言,也印证了跟单一目标收益跟踪误差投资组合优化模型最终选择较大情景下各资产的权重的结论。综上所述,单一目标收益跟踪误差投资组合优化模型对于提高组合收益、分散组合风险是有效的,对于中国资本市场资产配置具有指导意义。
(二)多目标收益跟踪误差投资组合鲁棒优化模型在基金中应用
多目标收益跟踪误差投资组合优化模型式转化为MATLAB Fmincon函数标准形式中处理式(3)转化为
式(14)时,2种情景下取不同目标收益,即γ1≠γ2,则:
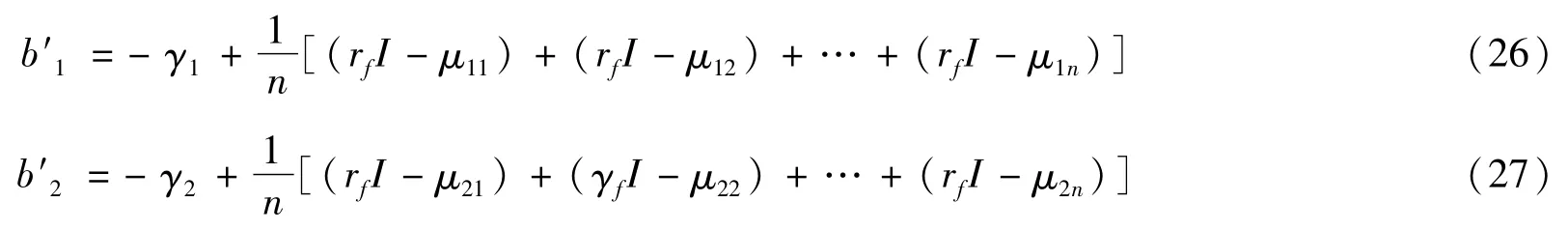
不同目标收益情况下,多目标收益跟踪误差投资组合鲁棒优化各资产权重、组合收益、组合风险如表3和表4所示。

表3 不同目标收益情况下多目标收益跟踪误差投资组合鲁棒情景1时优化结果
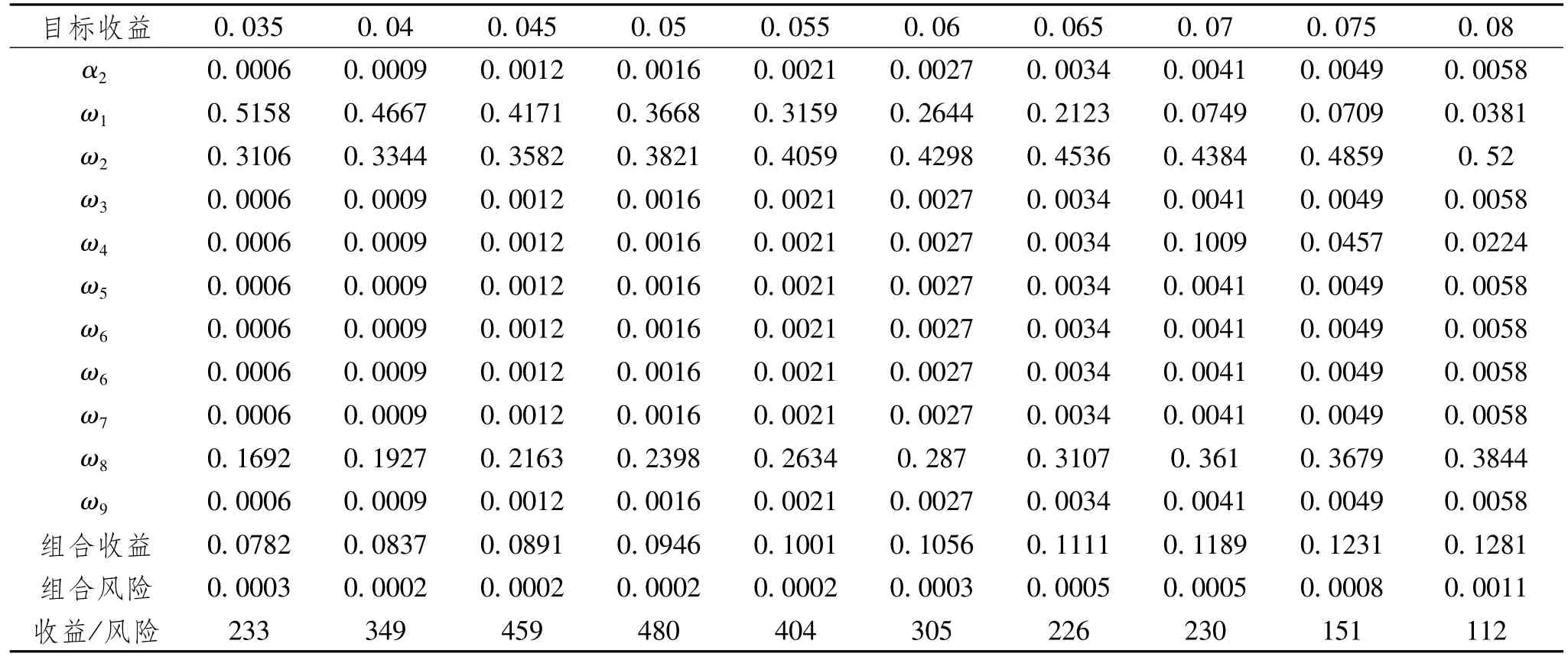
表4 不同目标收益情况下多目标收益跟踪误差投资组合鲁棒情景2时优化结果
如表3所示,在不同目标收益下,各资产权重发生变化,即进一步验证了多目标收益跟踪误差投资组合优化模型相比单一目标收益模型更具有合理性;投资组合实际收益率高于目标收益,表明多目标收益跟踪误差投资组合优化情景1时对于提高组合收益表现具有较好的表现;在目标收益递增的过程中,投资组合实际收益也伴随着目标收益逐步增加,投资组合风险先下降、后上升,在目标收益为0.065时组合风险达到最小-0.00003,投资组合风险总体呈现下降趋势,多目标收益跟踪误差投资组合优化情景1时不仅在提高收益方面表现优异,在分散风险方面同样有效;多目标收益跟踪误差投资组合优化情景1时在目标收益γ1=0.065
时、偏差波动的上界变量为α1=0.0031投资组合绩效最高,与表3均高于基金实际和基准模型投资绩效。
表3与表4具有组合收益显著高于目标收益的情况。但是多目标收益跟踪误差投资组合鲁棒情景2下组合风险与情景1不同,组合风险在随着目标收益的增加而增加,没有出现反转现象。情景2多目标收益跟踪误差投资组合优化模型在目标收益γ1=0.05时、偏差波动的上界变量为α1=0.0016投资组合绩效最高,与表2相比投资绩效同样均高于基金实际权重投资绩效和基准模型投资绩效。
结合表3和表4,根据投资组合绩效分析,多目标收益跟踪误差投资组合鲁棒优化模型在情景1时和情景2时,最终会选择在情景1时,目标收益为γ1=0.065、偏差波动的上界变量为投资组合权重,与表2相比,多目标收益跟踪误差投资组合鲁棒优化模型相比单一目标收益模型在提高收益、降低风险方面表现更为有效。
综上所述,在相同情景下不同目标收益γk会改变投资组合权重,影响投资组合收益与风险走势,从而影响投资组合投资绩效,因此,需要根据不同的市场预期下确定不同投资目标收益,再根据投资绩效分析,从而确定更优的投资组合权重。
(三)基于交易成本单一目标收益跟踪误差投资组合鲁棒优化模型实证分析
采用与Zheng和Liang[10]、王春峰等[11]相同的交易成本函数:TCi(ωi)=aiωi+bi,i=1,2,...,n,同样忽略固定交易成本对资产权重的影响,则变为:TCi(ωi)=aiωi,0<αi<1。假定交易成本函数TCi(ωi)=0.003ωi,即百分之一的投资权重将产生万分之三的交易成本。根据上述则投资组合基本权重为。
基于交易成本单一目标收益跟踪误差投资组合优化模型转化为MATLAB Fmincon函数标准形式方法与上述相同。
利用MATLAB Fmincon函数求解得情景1与情景2资产权重及投资绩效如表5所示:

表5 基于交易成本单一目标跟踪误差投资组合鲁棒优化模型结果及绩效分析
由表5可见,基于交易成本单一目标跟踪误差投资组合鲁棒优化模型情景1和情景2的收益率均低于与未引入交易成本的单一目标模型的收益率(见表2),再次印证引入交易成本会降低投资组合收益率;根据投资绩效分析,基于交易成本单一目标模型情景1投资效率高于情景2投资效率,这与单一目标模型结果相反,表明引入交易成本后会影响投资决策,也许会产生截然不同的结果。
四、结 论
本文研究了跟踪误差投资组合鲁棒优化模型及其衍生模型在中国资本市场的应用:
1.给出了跟踪误差投资组合鲁棒优化模型即单一目标收益跟踪误差投资组合鲁棒优化模型以及利用MATLAB Fmincon函数求解的具体算法,并采用光大保德信均衡竞选股票基金数据进行了实证分析,将跟踪误差投资组合鲁棒优化模型与基金实际投资绩效和基准组合投资绩效进行比较,表明单一目标收益跟踪误差投资组合鲁棒优化模型在提高投资组合收益、降低风险方面的适用性。
2.基于跟踪误差投资组合鲁棒优化模型提出多目标收益模型和基于交易成本单一目标收益模型及利用MATLAB Fmincon函数求解的具体算法。基于实证分析,依据不同市场预期采用不同目标收益的多目标收益
跟踪误差投资组合鲁棒优化模型相比单一目标收益模型、基金实际情况和基准组合投资更有效。同时以光大保德信均衡竞选股票基金数据进行实证分析,给出了基于交易成本单一目标收益跟踪误差投资组合鲁棒优化模型利用MATLAB Fmincon函数求解的具体算法及结果。
另外,在本文的基础上可以提出依据不同市场预期采用不同目标收益及引入交易成本函数的基于交易成本多目标收益跟踪误差投资组合鲁棒优化模型,具体思想和方法可以参考多目标收益模型和基于交易成本单一目标收益模型。
[1]MAEKOWITZ H.Portfolio Selection[J].Journal of Finance,1952,7(1):77-91.
[2]ROLL R.A Mean/Variance Analysis of Tracking Error[J].The Journal of Portfolio Management,1992,18(4):13-22.
[3]RUDOLF M,WOLTER H J,ZIMMERMANN H.A Linear Model for Tracking Error Minimization[J].Journal of Banking&Finance,1999,23(1):85-103.
[4]王秀国,邱菀华.跟踪误差多因素投资组合决策模型[J].管理评论,2007,18(11):59-62.
[5]罗金川,房勇.基于分层PCA的指数跟踪及实证[J].中国管理科学,2013,21(专辑):355-359.
[6]BLACK F,LITTERMAN R B.Asset Allocation:Combining Investor Views with Market Equilibrium[J].The Journal of Fixed Income,1991,1(2):7-18.
[7]COSTA O L V,PAIVA A C.Robust Portfolio Selection Using Linear-matrix Inequalities[J].Journal of Economic Dynamics and Control,2002,26(6):889-909.
[8]高莹,李超君,唐诗源.基于鲁棒优化的投资组合模型在投资基金中的应用[J].东北大学学报(自然科学版),2009,30(2):295-297.
[9]康志林.均值—绝对离差投资组合修正模型[J].华侨大学学报(自然科学版),2013,33(2):83-88.
[10]ZHENG D,LIANG X.Optimization of Tracking Error for Robust Portfolio of Risk Assets with Transaction Cost[J].iBusiness,2013(5):23-26.
[11]王春峰,杨建林,赵欣.具有典型交易成本的投资组合管理模型及其求解[J].系统工程理论与实践,2002,22(10):134-138.
Application of Tracking Error Investment Portfolio Robust Optimization Model and Its Derivative Models in Fund Market
WANG Zhiqiang,ZHAO Qing
(School of Finance,Dongbei University of Finance and Economics,Dalian 116025,China)
Based on the Tracking Error Investment Portfolio Robust Optimization Model,three derivative models are proposed,i.e.single target return model,multi-target return model and cost-based single target return model,and the methods to solve MATLAB are also presented.The“Everbright Prudential Balanced Campaign Stock Fund”data are empirically analyzed,the results of which are compared with the benchmark model and the actual investment performance of the fund.The research findings show that the three derivative models prove effective and feasible in improving return and reducing risk,and have
ignificance for asset allocation.
tracking error;investment portfolio;robust optimization;fund market
F830.91
A
2095-929X(2015)01-0001-08
(责任编辑 高 琼)
2014-09-21
国家自然科学基金项目“基于时变参数的学习机制、利率行为与政策效果研究”(71173030)。
王志强,男,辽宁大连人,东北财经大学金融学院教授,博士生导师,研究方向:金融工程;赵庆,男,满族,辽宁大连人,东北财经大学金融学院博士研究生,研究方向:金融工程。

