应用动力学拐角频率对经验格林函数法的改进

夏 晨 赵伯明

(北京交通大学土木建筑工程学院，北京 100044)

0 引言

近年来全球范围大地震频发，比如1989年美国Lama Prieta地震、1995年日本Kobe地震、1999年台湾集集地震、1999年土耳其Kocaeli地震、2005年印尼苏门答腊岛地震、2008年中国汶川大地震以及2011年东日本大地震。这些地震给人类带来巨大灾难的同时，也极大丰富了近场强震记录。地震学及地震工程学界普遍认识到，近场强地面预测对减轻未来大地震造成的灾害和指导工程建设的抗震设计具有重要作用。如何对未来大地震的强地面运动进行可靠预测，是地震学和地震工程所面临的重大挑战之一，也是地震学发展的成果应用到地震工程的一个桥梁。

经验格林函数法是地震动数值模拟计算中常用的方法之一，其基本思想是:大震产生的地面运动是由大震断层中一系列子源所产生的地面运动叠加而成，子源的地震动由大震附近的余震记录表示。该方法由Hartzell(1978)首次提出，其优点在于余震记录包含震源、传播路径和场地效应(地震动模拟中最重要的3个要素)的影响，避免理论数值计算的复杂过程以及对地下传播介质信息的依赖。运用经验格林函数法合成强地震动，关键在于小震记录的选取，作为格林函数的小震应与大震震源位置相近，震源机制解相似。从理论上考虑，小震的震级越小越接近点源，叠加合成时越符合大震的震源时间函数。但在实际应用中，小震级的地震记录是有限的，另外，震级太小时，记录的信噪比不高，将会影响结果的可靠性。

Hartzell提出经验格林函数法之后，得到广泛关注，多位学者对此方法进行改进并用于近场强地震动模拟(Kanamori，1979;Tanaka，1982;Irikura，1983，1986;Joyner et al.，1986;Heaton et al.，1989;Hutchings，1991;Kamae et al.，1992;Frankel，1995;Hough，2001;罗齐峰等，1994;金星等，2002)。在叠加小震记录时，对于所叠加的小震记录数量选取，有2种常用的准则。第1种是所叠加的小震数为N(假设大小震地震矩之比为N);第2种是所叠加的小震数为N2/3，即等于大小震的断层面面积之比。为后文表述方便，记第1种为A方法，第2种为B方法。在实际应用中，这2种方法均有缺陷。A方法合成的地震动在低频部分符合观测记录，但是高频部分偏高;B方法合成的地震动在高频部分符合观测记录，但是低频部分偏低。对这些缺陷，Joyner等(1986)提出随机叠加N4/3个小震记录，对叠加后的结果乘以系数N－1/3，以便得到高频和低频均较为理想的结果。一些学者提出将小震记录与随机震源时间函数求卷积，再叠加N个小震记录，不改变低频结果，降低高频结果。另一些学者提出叠加N2/3个记录，再采用相应的过滤器在不改变高频结果的情况下提高低频结果(Frankel，1995)。

在传统经验格林函数方法中，未考虑大小地震拐角频率的差异，由经验格林函数法合成的大震记录，其拐角频率等于所用的小震拐角频率，而实际中拐角频率随地震震级的增大而减小。这是引起经验格林函数法合成结果不能在高频和低频同时符合观测记录的一个重要因素。考虑大小震拐角频率的不同，基于ω2震源谱模型，通过理论推导构建一个新的函数，将动力学拐角频率引入到经验格林函数法(B方法)中，改进其合成的结果，并运用改进后的方法合成汶川大地震近场强地震动，通过与观测记录对比，验证动力学拐角频率在经验格林函数法中的有效性。

1 方法介绍

1.1 经验格林函数法原理

以Tanaka(1982)提出的一个经验格林函数法为B方法的代表。Tanaka(1982)基于大震与小震的定标关系，导出如下关系(Kanamori et al.，1975):

式(1)中:L，W，D，τ，M0分别为大震的震源长度、宽度、断层面平均位移、上升时间和地震矩;Le，We，De，τe，M0e分别为小震的相应参数。大地震的断层面由n2个大小相同的子源构成，每个子源与小震大小相同。将小震记录ae(t)作为子源格林函数，叠加合成大地震的地震动记录a(t)，如下所示:

式(2)、(3)中，c和v分别为地震波传播速度和破裂传播速度;Re表示小震震源到观测点的距离;R0表示大震断层面破裂点到观测点的距离;Rij表示第ij个子源到观测点的距离;rij表示第ij个子源到破裂起始点的距离。

在实际计算中，式(2)的叠加过程是在频域中完成的，其表达式如下:

式(4)中:Ae(f)为小震记录ae(t)的傅立叶变换。将叠加之和A(f)通过傅立叶逆变换转换到时域，即可得到大地震的地震动记录a(t)。

考虑到大小震应力降Δσ的差异，在文中采用Tanaka(1982)经验格林函数法时，式(4)改写为如下形式:

1.2 改进的思路及过程

传统的经验格林函数方法未考虑大小地震拐角频率的差异，合成的大地震具有与小地震相同的拐角频率，这不符合拐角频率随震级增大而减小的实际规律。这也是导致经验格林函数法(B方法)模拟结果与观测记录在低频出现差异的主要因素之一。

Motazedian等(2005)提出动力学拐角频率，将第ij个子源的拐角频率表示为

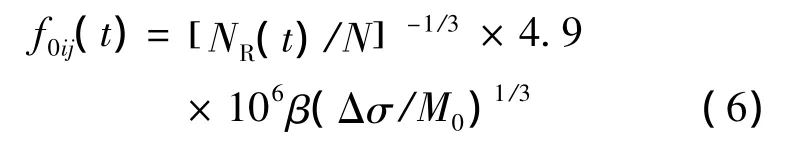
式(6)中，N为主断层面上的子源总数，NR为破裂传播到第ij个子源时累计滑动的子源个数，β为介质剪切波速，Δσ为主断层应力降，M0为主断层地震矩。用动力学拐角频率f0ij替代Boore(1983)随机点源模型方法中的拐角频率f0，再将随机点源模型方法计算的点源地震动作为子源的格林函数，运用随机有限断层模型程序EXSIM叠加合成主断层地震动。由于拐角频率在每个子源的计算中是显式的，因此动力学拐角频率可方便地引入到程序EXSIM中进行应用。

孙晓丹等(2009)提出一种与震源谱模型相关的动力学拐角频率，改善原来的动力学拐角频率定义中对破裂面上地震波频率辐射的不均匀性表达，考虑到拐角频率随破裂面积增加而有所下降的趋势。

但是，在经验格林函数法中，每个子源的信息包含在小震记录里，拐角频率并不体现在计算过程中。若将动力学拐角频率引入到经验格林函数法中，需要做一些处理。

假设大小地震的震源谱均符合Brune(1970)的ω2模型:

图1 经验格林函数法采用的主震断层模型(Tanaka，1982)Fig.1 The main fault plane model described by Tanaka(1982).

对于小地震，其拐角频率f0small通过地震动记录反演得到;对于每个子源，假设f0ij与累计滑动的子源个数NR的平方根成反比，表示如下:

式(8)中，f0main为主断层地震的拐角频率，其余参数与上文一致。在Boore(1983)随机点源模型方法中，拐角频率由式(9)计算获得:

由式(9)，可得

假设把已经滑动的NR个子源组成一个断层面，这NR个子源的总地震矩为M0ruptured，基于大震与小震断层参数的定标关系(Kanamori et al.，1975)，可以得到如下关系式:

由式(8)，(11)和(12)，可以得到如下关系:

由式(13)可以看出，动力学拐角频率f0ij与已发生破裂子源的总地震矩M0ruptured立方根成反比。将NR个子源看作一个断层面，式(13)具有与式(9)同样的意义，即

基于ω2模型，为引入动力学拐角频率f0ij到经验格林函数法中，构建一个函数如下:

为保证Hij(f)在高频(高于小震拐角频率的频段)时接近1，即函数Hij(f)不影响经验格林函数法高频计算的结果，参数Cij必须满足以下条件:

由式(8)，(10)和(15)，可得

进而，函数Hij(f)可表达为

函数Hij(f)与Frankel(1995)提出的相对滑移速度函数具有相似的形式，这是因为这2个函数都是基于ω2模型构建的，但是，二者在计算参数时基于不同的假设。Frankel(1995)基于所有叠加的子源地震矩之和与主断层地震矩相等这一假设，计算参数C和f0ij，得出f0ij与成正比。本文对于每个子源，假设f0ij与累计滑动的子源个数NR的平方根成反比，且Hij(f)在高频(高于小震拐角频率的频段)时接近1，即函数Hij(f)不影响经验格林函数法高频计算的结果，由此得出动力学拐角频率f0ij与已发生破裂子源的总地震矩M0ruptured立方根成反比，即f0ij∝M0ruptured－1/3。可以看出，在Frankel(1995)的研究中，f0ij是不变量，本文中f0ij随破裂传播而变化。

函数Hij(f)可以方便地与经验格林函数法结合，以引入动力学拐角频率f0ij。引入函数Hij(f)后的式(5)改写为

改进后的经验格林函数法可方便地实现，其过程如图2所示。

2 改进方法的验证——以汶川大地震地震动模拟为例

为检验动力学拐角频率引入经验格林函数法的有效性，分别运用改进前后的方法对汶川大地震主震断层周围6个台站点的地震动进行模拟计算。通过对比改进前后合成结果与观测记录的加速度反应谱，验证动力学拐角频率对合成结果低频成分的提高效果。

2.1 汶川地震基本参数

2008年5月12日14点28分(北京时间)，在青藏高原东缘的龙门山断裂带上发生特大地震，简称5·12汶川地震，其震级为MW7.9;起始破裂点(震中)位于30.986°N，103.364°E;震源深度19km;震源破裂长度达300km，宽40km。

多位学者通过远场体波波形记录结合近场强地震动数据，以及GPS和SAR等数据，利用反演技术重建汶川地震的震源破裂过程(Ji et al.，2008;Shen et al.，2008;王卫民等，2008;Yarai et al.，2008;Koketsu，2009)。Koketsu(2009)的反演结果显示，震源断层面由西南段和东北段两部分构成，如图3所示。整个断层面长300km，宽40km。两部分的走向均接近230°，西南段的倾角为35°，东北段的倾角65°。

Kurahashi等(2010)根据近断层6个台站的强震记录，提出震源断层存在4个凹凸体(asperity)，其中3个在西南段，1个在东北段上，地震动主要由西南段上的3个凹凸体引起。本文采用Koketsu(2009)的反演结果作为震源模型，并采用Kurahashi等(2010)建议的凹凸体参数(表1)，其分布如图4所示。选取3个余震的记录分别作为3个凹凸体区域的格林函数，余震参数见表2，其分布如图4所示。图4中，3个黑色圆点为所取3个余震的震中位置;HSL为黑水双溜索台站，JYC为江油重华台站，LDD为泸定得妥台站，LXT为理县桃坪台站，MXD为茂县叠溪台站，SPA为松潘安宏台站。

2.2 地震动模拟

选取主震断层周围6个台站(HSL，JYC，LDD，LXT，MXD，SPA)，空间分布如图4所示。参照上文中的震源模型，分别采用未修改的经验格林函数法和引入动力学拐角频率后的经验格林函数法合成汶川地震近场强震记录。合成结果和观测记录都采用四阶Butterworth滤波器进行0.5～20Hz的带通滤波。改进前后的合成结果与观测记录的加速度反应谱如图5所示，加速度时程如图6所示。

图2 改进后的经验格林函数法实施过程示意图Fig.2 The schematic diagram of improved empirical Green's function method.

图3 汶川地震断层面上的破裂滑动分布(引自Koketsu et al.，2009)Fig.3 Inverted slip distribution on the fault plane of Wenchuan earthquake(after Koketsu et al.，2009).

2.3 模拟结果及讨论

从图5所示的加速度反应谱对比可以看出，未修改的经验格林函数法合成结果(黑色虚线)在低频部分明显低于观测记录的结果(黑色粗实线)，引入动力学拐角频率后的合成结果(灰色细实线)提高了低频部分结果，高频部分结果基本不变化，低频部分提高后与观测记录接近。尤其在HSL、LDD和SPA 3个台站，低频部分的结果与观测记录符合度较高。部分台站模拟的结果与观测记录有差异，比如JYC的合成结果，引起差异最重要的原因是破裂传播效应，而经验格林函数法不能包含这部分因素对合成结果的影响。本文重点在于验证引入动力学拐角频率后，经验格林函数法合成的低频地震动结果是否得到了有效提高。从这方面看，图5中6个台站的结果显示，改进后的方法对于改善经验格林函数法的低频结果是有效的。

表1 凹凸体参数(引自Kurahashi et al.，2010)Table 1 Parameters of the asperities(Kurahashi et al.，2010)

图4 震源断层凹凸体，余震震中，以及若干台站分布图(修改自Kurahashi et al.，2010)Fig.4 The locations of asperities，epicenters of aftershocks and some of the stations(adapted from Kurahashi et al.，2010).

表2 选取的余震相关参数Table 2 List of parameters of selected aftershocks

图5 观测记录与合成结果的加速度反应谱对比图Fig.5 Comparison of acceleration spectra of observed and synthesized ground motions.

图6 观测记录与合成结果的加速度波形对比图(1)Fig.6 Comparison of observed and synthesized acceleration waveforms(1).

图6 观测记录与合成结果的加速度波形对比图(2)Fig.6 Comparison of observed and synthesized acceleration waveforms(2).

图6对比了引入动力学拐角频率之后合成的加速度波形图与实际记录的加速度波形图。大部分台站合成的加速度波形接近观测的波形，加速度峰值比在0.5～2。LDD和LXT台站的水平分量结果偏大。JYC台站的结果在65～80s与实际记录有明显差异，这是由于在本文的模拟中，只取西南段的发震断层作为震源，因此JYC的结果在70～80s缺少西北段断层引起的地震动。但是西南段的结果与实际记录较为符合。

3 结论

本文从大小震拐角频率差异为出发点，假设主断层上每个子源的拐角频率与累计滑动的子源个数平方根成反比，基于ω2震源谱模型，通过理论推导构建一个新的函数，将动力学拐角频率引入传统经验格林函数法中。以Koketsu(2009)的震源过程反演结果作为震源模型，并参考Kurahashi(2010)建议的凹凸体参数，分别用改进前和引入动力学拐角频率后的经验格林函数法合成5·12汶川地震近场强地面运动加速度时程。合成结果分别与观测记录的加速度反应谱，以及加速度波形图进行了对比。

(1)通过比较合成和观测的加速度反应谱，未修改经验格林函数法的大部分结果在低频相对观测结果偏低;而引入动力学拐角频率的合成结果在低频部分明显提高，并与观测结果较为符合，其高频部分基本保持不变。动力学拐角频率引入经验格林函数法后有效地改进了合成的结果。

(2)汶川大地震地震动合成计算显示，从加速度反应谱以及加速度波形图可看出，大部分合成结果与观测记录是符合的，说明经验格林函数法对于MW7.9地震的地震动计算同样有效。经验格林函数法可对未来可能发生的大地震地震动进行预测。