高速铁路设计线形上任意里程处切线方位角的计算
聂虎啸,刘成龙,王化光,陈 龙
(1.西南交通大学 地球科学与环境工程学院,四川 成都612756;2.成都市勘察测绘研究院,四川 成都610081)
在高速铁路和客运专线等快速铁路中,由于列车运行速度的提高,对线路平顺性的要求很高[1];而线路的平顺性,主要由轨道的几何状态参数来评价[2]。这些轨道几何状态参数正确与否,直接关系到机车车辆能否安全运行。要计算轨道几何状态参数中的轨向和矢距以及线路设计线形上任意里程点处的平面坐标,线路设计线形上任意里程处的切线方位角是必要数据。可见,线路设计线形上任意里程点处切线方位角的计算,是进行轨道测量及其平顺性检测的基础,因此,研究线路设计线形上任意里程点处切线方位角的计算方法是必要的。然而,如今线路设计线形上任意里程点处切线方位角的计算方法过于零散,给轨道平顺性的检测带来了诸多不便,尤其不利于轨道平顺性检测数据处理的程序化。因此,本文结合相关的线路、高速铁路测量理论和数学知识,探讨线路设计线形上任意里程处切线方位角计算的方法,为今后轨道几何状态参数的编程计算提供依据。
1 线形判断
高速铁路线路中线的第一类平面设计文件,包括线路上各个曲线处四大桩点的里程、平面坐标以及切线方位角,即直缓点(ZH)的里程、平面坐标(xZH,yZH)、坐标方位角αZH,缓圆点(HY)的里程lHY、平面坐标 (xHY,yHY)、坐标方位角αHY,圆缓点(YH)的里程lYH、平面坐标 (xYH,yYH)、坐标方位角αYH,缓直点(HZ)的里程lHZ、平面坐标 (xHZ,yHZ)、坐标方位角αHZ。
铁路平面线形由直线、圆曲线和缓和曲线组成。计算任意里程处切线方位角,首先将指定点的里程与设计文件中的四大桩点的里程进行比较,从而判断指定点所处位置的线形;然后根据点的位置分三种情况对该点处切线的方位角进行计算,即点在直线、缓和曲线和圆曲线上三种不同情况下切线方位角的计算。
将线路上指定点的里程,与线路设计文件中各个曲线的四大桩点的里程进行比较,判断该里程处于哪两个相近大桩点之间,该点就处于这两个大桩点所夹的线形上。例如,给定一个里程,与线路上四大桩点的里程进行比较,发现该里程处于直缓点和缓圆点的里程之间,那么,可以判断,该点位于缓和曲线上。上述过程就是指定里程点所处线形判断的过程,它是进行线路设计线形上任意里程点处切线方位角计算的基础。
2 直线段切线方位角计算
当指定里程点位于直线段时,为了方便计算该点处的切线方位角,可将点的位置分为直缓点之前和缓直点之后两种情况。
当指定的里程点位于直缓点之前的直线上时,根据直缓点处的切线方位角,可以确定直线上任意里程点处的切线方位角α:

式中:αZH为直缓点设计切线方位角。
当指定的里程点位于缓直点之后的直线段上时,根据缓直点处的切线方位角,可以确定直线上任意里程点处的切线方位角α:

式中:αHZ为缓直点设计切线方位角。
3 缓和曲线段时切线方位角计算
当指定里程点位于缓和曲线段时,建立以直缓点(ZHD)或缓直点(HZD)为坐标系原点、以直缓点或缓直点处的切线为x轴的缓和曲线段独立坐标系。如图1所示,图中β为缓和曲线上任意里程点处切线与x轴的夹角。
由图1可知,在缓和曲线上任意里程点处(设为P点)前进方向的切线方位角α计算:
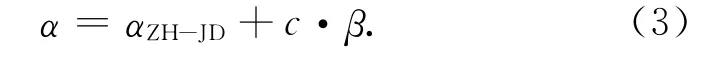
式中:αZH-JD为直缓点到交点的设计坐标方位角,即与直缓点处切线方位角等同;β为缓和曲线上点的切线与x轴的夹角;c为线路方向定向因子,沿前进方向线路左偏时c=-1,右偏时c=1;图1中的线路为左偏。
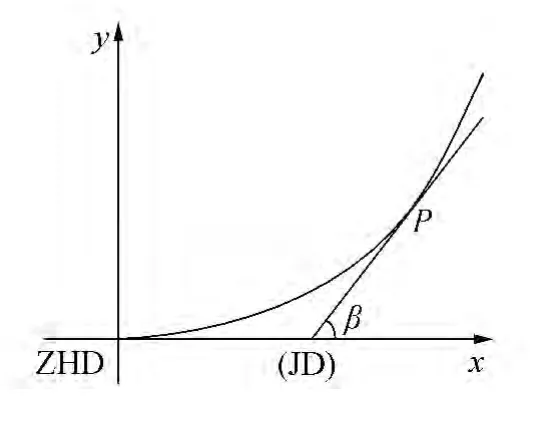
图1 直缓点独立坐标系
设ρ为该点处的曲线曲率半径;l为P点至直缓点的缓和曲线长;l0为缓和曲线总长。R为圆曲线的半径[5]。
首先计算P点至直缓点的缓和曲线长:

式中:LP为P 点的里程;LZH为直缓点的设计里程。
由图(1)可知:dβ=dl/ρ,同时缓和曲线方程满足:ρl=Rl0,由以上两式可得:dβ=l·dl/(Rl0)
积分得

可得缓和曲线上指定里程点处前进方向的切线方位角为

同理,若以缓直点(HZD)为原点建立缓直点独立坐标系,如图2所示,则圆缓点至缓直点之间的缓和曲线上任意里程点处前进方向的切线方位角

式中:l=LP-LHZ;cc为线路方向定向因子,当沿前进方向线路左偏时cc取1,右偏时cc取-1;图2中的线路为右偏。
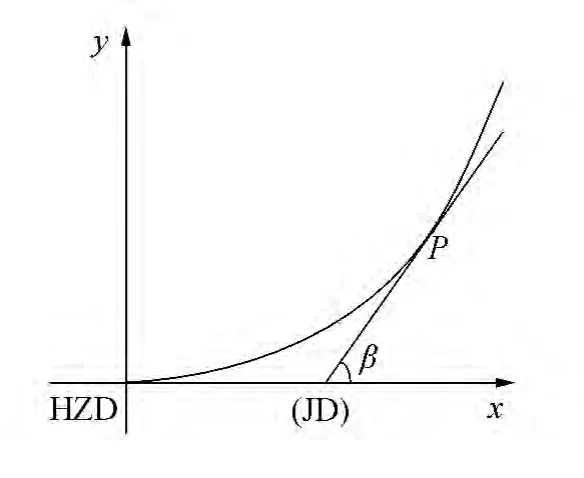
图2 缓直点独立坐标系
4 圆曲线段时切线方位角计算
当指定里程点位于圆曲线段时,以缓圆点(HYD)为坐标原点,缓圆点的切线方向为x轴,切线的垂线为y轴,建立圆曲线独立坐标系[6-10]。如图3所示,图中β为圆曲线上点的切线与x轴的夹角,γ为P点的弦切角,ψ为圆心角。
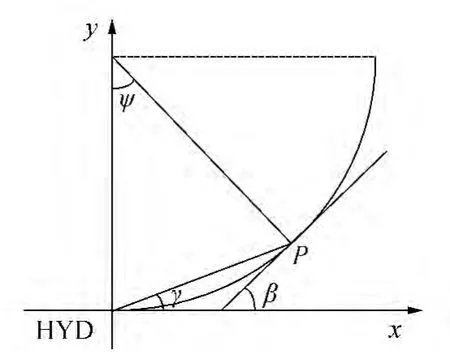
图3 圆曲线独立坐标系
由图3,圆曲线任意里程点处切线方位角
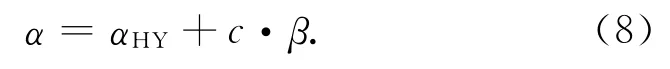
式中:αHY为缓圆点处切线设计方位角,β为圆曲线上任意点处切线与x轴的夹角,沿前进方向线路左偏时c=-1,右偏时c=1。
其中αHY已由设计文件给出,β计算方法如下:
由指定点P的里程lp、缓圆点的里程lHY可得P点至缓圆点的曲线长:

由几何关系可得圆心角:

由图3可知曲线上P点的切线角:

式中:γ为HYD点的弦切角。
那么由式(8)、式(9)和式(10)可得圆曲线上指定里程点前进方向的切线方位角为

5 算例分析
本文推导线路设计线形上任意里程点处的切线方位角计算公式,为验证其正确性与可行性,选取某高速铁路的部分线路设计文件进行计算分析。某高速铁路平面线形的部分线路设计文件如表1所示,按照推导公式计算的前进方向的切线方位角如表2所示。

表1 国内某高速铁路平面线形的部分设计文件

表2 部分给定里程点前进方向的切线方位角计算结果
显然,缓圆点既在缓和曲线上又在圆曲线上。从上表2中计算的结果可以看出,利用缓和曲线上任意里程点前进方向切线方位角的计算公式,得到的缓圆点处切线方位角与设计的方位角相同;同样,对于圆缓点,分别利用圆曲线和缓和曲线上任意里程点前进方向切线方位角的公式进行计算,得到的圆缓点处切线方位角也相同,充分说明本文推倒的公式是准确无误的,推导出的公式可以应用于高速铁路轨道几何状态参数的计算和平顺性检测中,也可作为编程计算轨道几何状态参数的算法之一。
6 结束语
本文结合线路、高速铁路测量和数学的相关知识,利用本文提出的指定里程点所在线形的判断方法,推导了线路设计线形上任意里程点处不同线形上切线方位角的计算公式,经实例计算验证,是一种正确并且实用的计算式。对今后线路测量的相关研究,尤其是对轨道平顺性几何状态参数的研究有一定的帮助,为轨道平顺性检测数据处理的程序化提供了算法。当然,轨道设计线形上任意里程点处切线方位角计算,只是轨道测量技术相关研究中的部分内容,应在此基础上继续对轨道平顺性检测的数据处理内容与方法进行深入研究。
[1]何华武.快速发展的中国高速铁路[J].中国铁路,2006(7):23-31.
[2]铁道部科学技术司.科技基(2008)86号客运专线轨道几何状态测量暂行技术条件[S].北京:中国铁路出版社,2008:1-31.
[3]李书亮.轨检仪的功能设计与实现[D].成都:西南交通大学,2008:1-55.
[4]李文彬,翟高鹏,花向红,等.基于Romberg积分的线路中线测设统一坐标模型算法实现[J].测绘工程,2014,23(6):27-30.
[5]王兆祥.铁道工程测量[M].北京:中国铁道出版社,2000:228-231.
[6]郑子天.客运专线轨检仪研制过程中的关键算法研究[D].成都:西南交通大学,2009:7-20.
[7]张强,刘成龙,周凌焱,等.铁路既有线复测平面曲线分区新方法[J].测绘工程,2014,23(8):59-61.
[8]闫广峰,高山.高速铁路CPⅢ网平差起算点兼容性研究[J].测绘工程,2014,23(8):50-53.
[9]同济大学数学系.高等数学第五版[M].北京:高等教育出版社,2002:154-158.
[10]张正禄.工程测量学[M].武汉:武汉大学出版社,2005:163-173.

