高精度GPS监测小范围区域沉降的分析
张 拯,张献州,刘 龙,黄惠峰
(西南交通大学 地球科学与环境工程学院,四川 成都610031)
随着GPS技术的发展,GPS短基线测量的应用日益广泛,例如变形监测网、矿井近井网、桥梁、隧道控制网等。注意到在这些小范围GPS网中,一般只关注GPS测量所得控制点的平面坐标,而忽视了高程测量结果。原因在于:目前,GPS定位平面测量精度可达10-6~10-9量级,可满足工程测量的要求。而GPS高程测量由于受观测误差和坐标系统不一致等因素的影响,其精度一直不高,仪器的标称精度也较平面定位精度低1倍,导致目前在利用GPS建立高精度控制网时平面和高程分开建立、分别处理的现象较为普遍,这在很大程度上限制了GPS技术的应用[1-2]。因此,有必要对高精度测量中GPS高程测量的可行性和精度进行研究,以使其更广泛地应用于测量领域,为我国的工程建设服务。
1 常用高程系统及其相互转换
1.1 常用高程系统
常用的高程系统依据其所采用基准面(高程起算面)的不同,主要分为3种:大地高系统、正高系统和正常高系统[3-4]。其中,大地高系统是以参考椭球面为基准面的高程系统,是法线高程系统,GPS高程属于大地高;正高系统是以大地水准面为基准面的高程系统,为垂线高程系统,故正高又称海拔高;正常高是以似大地水准面为基准面的高程系统,为我国高程测量所采用的高程系统[5-6]。尽管近50年来我国仍采用正常高系统,但随着时代的发展、研究的深入,如今推求正高的精度又与正常高的非常接近,况且它又符合我国幅员广大的高海拔山区的实际情况,因此,用正高系统代替正常高系统的观念将会被人们所接受。
1.2 各高程系统之间的相互转换
3种高程系统关系如图1所示。

图1 3种高程系统关系示意图
1)大地高与正常高之间的转换关系为

式中:H为大地高,Hγ为正常高,δ为高程异常(似大地水准面与参考椭球面之间的距离)。
2)大地高与正高之间的转换关系为

式中:Hg为正高,N为大地水准面差距(大地水准面沿法线到地球椭球体面的距离)。
2 GPS区域沉降监测可行性探讨
基于GPS所测的大地高,若能获得监测点的高程异常δ或大地水准面差距N,便可计算出监测点的正常高或者正高[7]。地表区域沉降监测要求以厘米甚至毫米级的精度获取监测点的高程变化值,但目前尚不能以毫米级的精度获得监测区域的高程异常值,因此,不可直接将GPS所测大地高与精密水准所测正常高进行高精度转换[8]。但是,注意到沉降监测所关注的是监测点的高程变化量Δh,而监测点的垂直变化量同样也可以以GPS所测大地高差ΔH来表示,ΔH与Δh之间的转换关系为

式中:cosα是监测点上垂线偏差的余弦,由于变形监测控制网的控制范围一般较小,在较小范围内可将垂线偏差α视作固定量,故可认为在控制网覆盖范围内cosα是一个定值,即ΔH与Δh之比是某一常数[2]。因此对于监测范围较小的区域,用GPS测量得到的大地高的变化来反映小范围区域沉降在理论上是可行的。
3 GPS区域沉降监测数据处理
3.1 监测区域介绍
某山岭隧道全长(斜长)1 983.0m,水平投影长度1 978.62m,设计坡度-41.4‰,轴线方向112°47′30″。该隧道安全对保证国家重点油气管线工程至关重要。由于隧址区构造运动活跃,可能引起隧址区南丘里塔格背斜核部发生层间错动,从而导致隧道衬砌承受挤压和剪切作用,由此引发衬砌沿轴向发生不同程度的挤压变形和剪切开裂。为了具体了解和掌握隧道变形隐患的演变过程,及时捕捉隧道变形的特征信息,对该隧道采用了包括GPS高精度和精密水准监测的综合监测方法。其中GPS全球定位系统技术为隧址区其他监测方法提供监测控制基准,同时用于监测隧道两端相对区域位移变化。精密水准路线方法为隧址区其他监测方法提供监测高程控制基准,同时用于监测隧道两端相对区域沉降变化。GPS控制网共布设4个GPS控制点(GPS1,GPS2,GPS3,GPS4),观测点采用永久性强制对中装置,水准基点埋设在GPS观测墩上,如图2所示。2011年11月进行了首期GPS与精密水准同步观测,以后每年每季度进行复测。GPS观测采用Trimble R6双频接收机以30s采样间隔连续观测4h,卫星截止高度角为15°。数据处理采用TGO(Trimble Geomatics Office)处理,并作三维自由网平差,计算结果表明,表征GPS数据观测质量的精度指标都满足《全球定位系统(GPS)测量规范》(GB/T18314-2009)中D级GPS网的要求。水准数据处理采用西南交通大学主导开发的GeoNMOS软件(登记号2012SR072212)处理,处理结果各项精度指标均满足《国家一、二等水准测量规范》(GB/T12897-2006)中二等水准测量的要求。
另外,为了宏观监测隧址区的区域变形发展,于2012年5月底开始在隧道进出口布设了GPS连续运行监测点(CORS),其所观测的实时数据经GPRS网络传输到GNSS Spider软中解算处理,解算后的坐标数据实时传输到Geomos Monitor软件中进行位移监测成果分析,实时反映隧址区域的区域变形情况。

图2 GPS控制点分布示意图
3.2 GPS与精密水准高程数据处理对比分析
为了研究GPS测量所得大地高应用于地表沉降监测的精度,选取2011年11月到2014年3月共12期GPS大地高变化和精密水准测量数据进行比较(见表1),以分析GPS大地高的测量精度及GPS和精密水准测量结果的一致性。

表1 GPS和精密水准所得各观测点的沉降量比较 mm
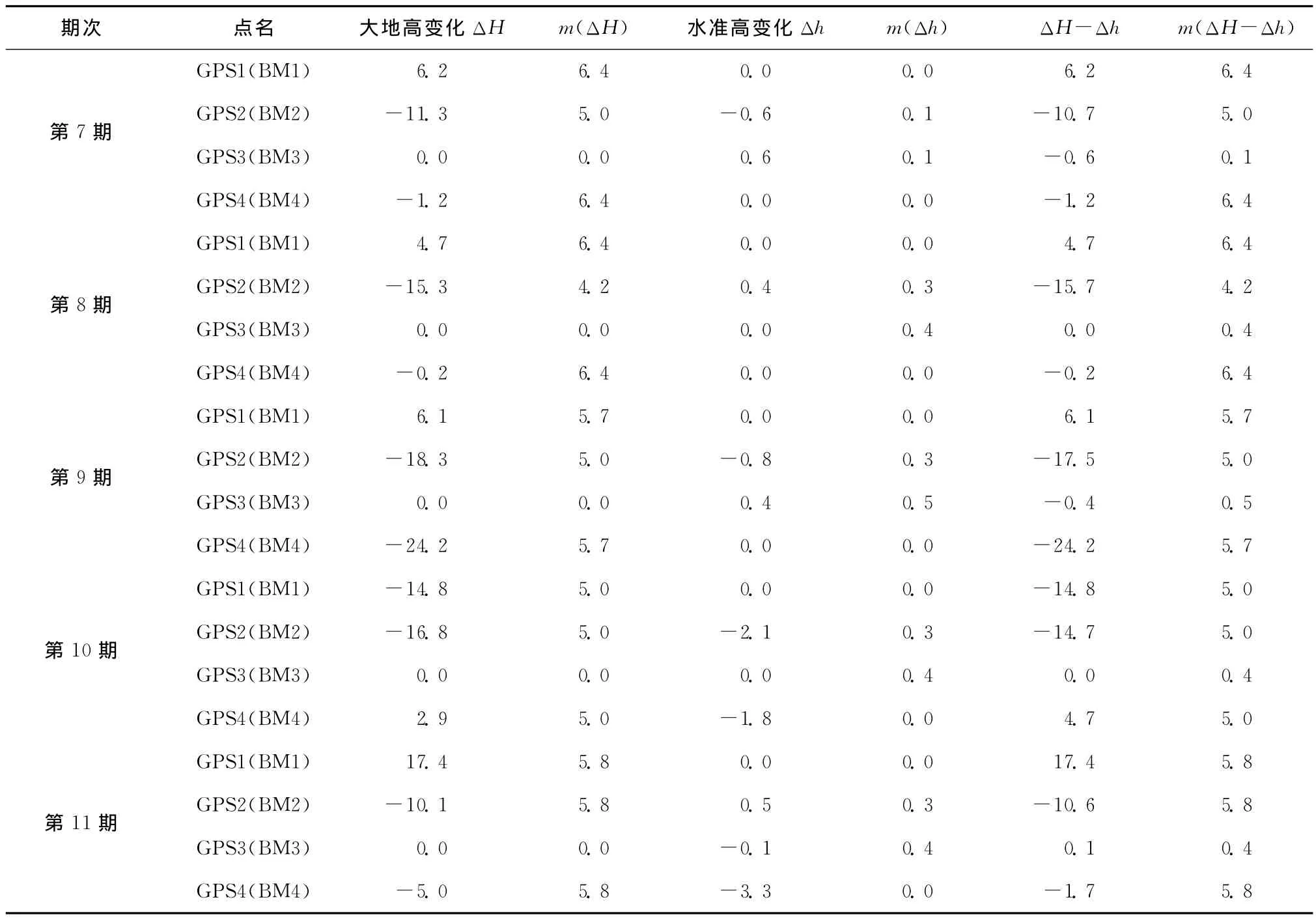
续表1 mm
说明:
1)“大地高变化ΔH”是由TGO软件解算得到的相应期GPS观测点的大地高变化(后一期减前一期,负号表示观测点下沉)。
2)“m(ΔH)”是由TGO软件解算得到相应期GPS观测点的大地高变化的中误差(后一期大地高中误差和前一期大地高中误差平方和再开方)。
3)“水准高变化Δh”是精密水准测量得到的相应期GPS观测墩底座上水准基准点盐水沟工程独立坐标系高程变化(后一期减前一期,负号表示观测点下沉)。
4)“m(Δh)”是后一期水准高中误差和前一期水准高中误差平方和再开方所得结果。此处水准基准点高程中误差是精密水准测量数据经GeoNMOS软件严密平差处理所得结果。
4 GPS区域沉降监测成果分析
基于上述理论分析和表1的对比结果可以看出:
1)隧道隧址区域GPS周期监测所得到的大地高变化与精密水准测量所得水准高变化所反映的隧址区域沉降情况基本一致,GPS测量与精密水准测量结果的差值大都在-30~20mm之间,如图3所示(受篇幅限制,图3中仅列出了前6期的数据)。
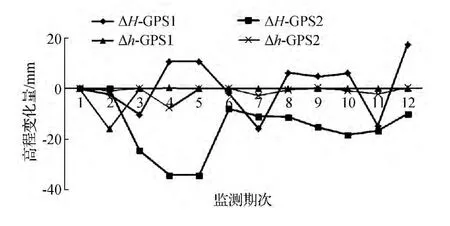
图3 大地高变化与水准高变化对比
2)选取GPS和精密水准监测结果差异较大的3个点进行分析,如表2所示。

表2 GPS和精密水准监测结果差异较大点统计
注意到:北京时间2012年6月15日5时51分,距该隧道约150km的某地发生5.4级地震,震中附近县城震感强烈;北京时间2012年6月30日5时7分,距该隧道约320km的某地发生6.6级地震;北京时间2012年6月30日8时46分,距该隧道约300km的某地发生4.2级地震。可以看出,较大差异发生的时间恰好与3次地震发生的时间重合,因此可以认为GPS所测大地高和精密水准所测正常高之间的较大差异是地震造成的。
此外,在这3次地震过程中,GPS连续运行站始终保持着对隧道进行连续监测,通过分析2012年6月15日、16日间隔10min的监测数据,可以发现在高程方向上,由于地震影响,基准点存在有下沉量(2cm左右),但变形量并未朝着某一个方向一直发展下去,以后其位移量摆动振幅变小,又趋于平稳,说明隧道在高程方向震后没有持续明显位移,这也从一个侧面提供了佐证,解释了表2中GPS和精密水准监测结果差异较大的原因。
3)根据表1做出统计,如表3所示。

表3 大地高变化中误差、水准高变化中误差以及两者较差中误差统计
从表3中统计数据可以看出,m(ΔH-Δh)值主要受到m(ΔH)以及m(Δh)的影响,相信随着GPS高程测量精度的提高,在今后的地面沉降监测中GPS将大有作为。
综上,通过对比分析GPS所测大地高变化和精密水准测量所得水准高变化,可以看出两者反映的区域沉降变形是基本一致的,GPS测量中采取有效的措施减小大地高测量误差m(ΔH)可在一定程度上提高GPS高程测量精度,从而其所获得的区域沉降数据也会更加精确、可靠。
5 结束语
本文研究应用GPS测量技术精确获取工程区域高程变化的方法,通过与精密水准测量(二等水准)区域高程变化数据对比分析,可知两者所反映的区域地面垂直变形量基本一致。从本文数据分析可知,隧道隧址区域地面并未发生明显沉降,整个隧道处于安全稳定状态。此外,结合GPS连续运行站,可实现对于区域沉降的实时宏观把控,实时变形数据也与精密水准沉降监测互为验证。对于水准基点相距很远、联测困难的沉降变形区域,采用GPS连续运行参考站作为沉降监测基准,可有效改善监测方案,节约成本,提高监测网的灵活性和精确度。本文所引数据量有限,且GPS控制网区域覆盖范围较小,对于大范围、沉降变形复杂的区域,利用GPS大地高变化进行区域沉降监测的精度还有待进一步研究。
[1]陈焕然.基于CORS站的GPS平面控制网起草点兼容性研究[J].测绘工程,2015,24(2):24-26.
[2]楚彬,范东明.基于比例整体最小二乘的GPS高程拟合[J].测绘工程,2014,23(4):37-39.
[3]杨建图,姜衍祥,周俊,等.GPS测量地面沉降的可靠性及精度分析[J].大地测量与地球动力学,2006,26(1):70-75.
[4]张赤军,边少锋.重力场中正高的理论与研究[J].地球科学进展,2005,20(4):455-458.
[5]黄立人,匡绍君,杨贵业.GPS观测得到的天津地区的现今变形[J].大地测量与地球动力学,2002,22(4):17-20.
[6]王强,崔希民,张恒璟,等.多项式拟合模型在GPS水准测量中的应用[J].测绘工程,2014,23(8):19-22.
[7]吴良才,胡振琪.GPS高程转换方法和正常高计算[J].测绘学院学报,2004,21(4):256-258.
[8]宁津生,郭春喜,王斌,等.我国陆地垂线偏差精化计算[J].武汉大学学报:信息科学版,2006,31(12):1035-1038.

