龙门山断裂带南段地壳一维P波速度结构*
王小娜,于湘伟,章文波,王思琳
0 引言
青藏高原东缘地壳物质向东移动的过程中受到扬子地块刚性的四川盆地阻挡,青藏高原推覆在扬子地块之上,在青藏高原和四川盆地之间形成了龙门山断裂带 (Royden,1996;Royden et al.,2008;Clark,Royden,2000;Klemperer,2006)。龙门山断裂带为NE—SW向逆冲兼右旋走滑断裂,是松潘—甘孜块体南东端边界,西接鲜水河—安宁河断裂带,南临四川盆地,北部为龙门山区,东部与秦岭南缘相接,是我国大陆南北地震构造带中段的重要组成部分 (徐锡伟,2009)。
龙门山断裂带平均海拔4 km,长约500 km,宽约40~50 km(张培震等,2008)。沿四川盆地西北缘底部切过,地壳厚度在此变化剧烈,其西为60~70 km,其东则在50 km以下。龙门山断裂带自西向东共由4条逆冲走滑断裂组成:龙门山后山断裂,龙门山中央断裂,龙门山前山断裂及龙门山山前隐伏断裂。每条断裂又分别由几条不同的段组成,断裂倾角在近地表较大,约为60°~70°,有的地方近直立,随深度向下逐渐变缓,在地下20~30 km处收敛成一条剪切带,成为青藏高原推覆在四川盆地之上的主控断裂 (滕吉文等,2008)。
近年来,随着龙门山断裂带地震危险性增加(Parsons et al.,2008;刘博研等,2008)。2008年5月12日四川省汶川县发生MS8.0地震,2013年4月20日四川省芦山县发生MS7.0地震,两次地震皆位于龙门山断裂带南段,因此为该区域的地震定位研究提供准确恰当的一维速度模型至关重要。此外,在实际工作中,地球三维复杂的速度结构为研究带来了困难,使用一维速度模型可以简化反演问题,因此本文将确定龙门山断裂带南段地壳一维 P波速度模型,为该地区地震重定位及地震层析成像等研究工作提供基础。
1 计算方法
地球内部物质分布、深部结构、地质构造、断裂带分布等增加了地球内部三维速度结构的复杂性,基于一维模型对非线性函数进行线性估计,能够简化三维反演问题。地震波走时tobs可表示为台站坐标 s,震源参数 h和速度场 m的非线性函数:其中走时和台站坐标已知,而震源参数和速度场未知。引入先验一维速度模型,根据射线追踪计算理论走时tcalc,则走时残差tres可表示为震源参数扰动Δh和模型参数扰动Δm的函数。在一维速度模型下,震源参数及模型参数之间存在高度的非线性关系,因此我们对式 (1)进行一次Taylor级数展开,进而获得走时残差tres与震源参数扰动Δhk和模型参数扰动Δmi的线性表示:
式中,e为走时误差,其包括观测误差,台站坐标、震源参数及速度模型引起的理论走时误差以及线性估计引起的误差。将式 (2)对应的震源—模型耦合问题表示为矩阵形式:
式中,t为走时残差向量,H为走时对震源参数的偏导数矩阵,h为震源参数扰动向量,M为走时对模型参数的偏导数矩阵,m为模型参数扰动向量,e为误差向量,A为所有未知参数偏导数矩阵,d为震源参数及模型参数扰动向量。
地震定位中,忽略震源位置和速度模型间的耦合关系会导致定位结果出现系统偏差,其定位误差严重依赖于先验模型 (Thurber,1992;Eberhart, Michael, 1993; Michael, 1988;Vander,Spakman,1989),不恰当的先验模型会导致解收敛于局部极小值 (Crosson,1976;Lee,Stewart,1981;Thurber,1985),因此我们需考虑震源—模型耦合问题 (Thurber,1992),并使用尽可能接近真实速度的一维速度模型。Kissling等 (1994,1995)提出了确定最小一维速度模型的方法 (VELEST程序),其基本思想是:(1)根据地质或地球物理信息建立n个初始参考模型;(2)选择高质量覆盖全区的直达波,反射波或折射波数据进行射线追踪;(3)通过阻尼最小二乘法使方差eTe最小化,进而反演震源参数和一维速度模型;(4)重复步骤 (2)和 (3),最终获得n个解,从中选取走时均方根残差(RMS)最小的解作为“最小一维速度模型”。通过上述步骤获得的“最小一维速度模型”与真实速度较为接近,且其对应的台站校正可以减小接收点处速度结构的影响,因此能够显著改进地震定位和层析成像的精度。
2 数据资料与反演计算
2.1 数据资料
本研究选取四川地震台网、重庆地震台网记录到的2009年1月1日至2013年5月6日发生在龙门山断裂带南段的P波震相数据 (郑秀芬等,2009)进行研究 (图1)。为保证数据质量的可靠性,选取P波走时残差0.5 s以内的震相,并剔除离散度较大的震相数据,最终挑选出14个地震台站记录的587个地震的P波到时数据5 012个 (图2),所挑选地震为ML≥2.0,且每个地震至少有8个台站记录。从射线分布图 (图1)可以看出,地震射线覆盖整个龙门山断裂带南段,震源深度范围0~30 km,且主要集中在10~25 km之间 (图3)。
为了保证模型速度能够涵盖较大的速度范围,我们参考以往研究工作中得到的速度结构信息,选取多种P波初始参考模型 (图4),以期获得全局最小RMS相对应的最优的速度模型。模型1和模型2:赵珠和张润生 (1987)将地壳视为水平分层均匀介质获得的青藏高原平均速度模型及四川盆地平均速度模型;模型3:赵珠等 (1997)修订的龙门山断裂带速度模型;模型4:Wang等(2007)在青藏高原东缘进行人工测深获得的四川盆地速度模型;模型5:杨智娴等 (2003)用于中国中西部地区的速度模型;模型6:结合地质与地球物理资料建立的一维速度模型;模型7:Wang等 (2007)在青藏高原东缘进行人工测深获得的青藏高原速度模型;模型8和模型9:黄媛等(2008)用于汶川地震定位的青藏高原速度模型和四川盆地速度模型;模型10:吴建平等 (2009)在汶川及周边区域速度结构研究中用到的速度模型;模型11和模型12:黄玉婷 (2012)进行龙门山地区地震绝对定位时所使用的青藏高原速度模型及四川盆地速度模型。
2.2 最小一维速度模型
为保证解的稳定性,我们对不同的控制参数(震源参数、速度参数及台站校正的阻尼系数)进行权衡分析,保证参数分辨率与数据方差达到最优均衡,最终选取的震源参数、速度参数及台站校正的阻尼系数分别为0.01、1.00及0.01。在反演过程中,当所有地震走时均方根残差 (RMS)明显减小,台站校正值和速度值变化微小时停止迭代,其最大迭代次数设为20。
通过对12种初始模型进行反演求解,获得的输出速度模型如图5所示,由12种速度模型的走时均方根残差 (RMS)分布图 (图6)可以看出,模型6获得的地震走时均方根残差 (RMS)变化较大,在第4次迭代时已接近稳定,经过9次迭代,其输出模型满足以下条件:(1)震源位置,台站校正值和速度值没有较大变化;(2)所有地震走时均方根残差 (RMS)明显减小;(3)最小一维速度模型和台站校正值有实际的地质意义且没有违反先验信息 (Kissling et al.,1995;Carla et al.,2003);(4)地震走时均方根残差 (RMS)最小,因此,我们选取模型6的输出模型为“最小一维速度模型”(表1)。
反演前后,最小一维速度模型的数据方差由1.45降为 0.07,走时均方根残差 (RMS)由0.88 s降为0.20 s,根据最小一维速度模型速度—深度关系图 (图5)可知,0~10 km处速度值与初始模型 (模型6)相差较大,其中0~3 km之间P波速度明显高于初始模型速度约1.11 km/s,这可能与台站校正的影响有关。3~6 km及6~10 km处速度值分别减少0.17 km/s和0.25 km/s。10 km处速度变化较为明显,从5.61 km/s迅速增加到6.14 km/s,其下方速度与初始模型相比整体变化不大,10~15 km速度值仅仅减少0.03 km/s。值得注意的是,15 km及25 km处为明显的速度间断面。15~25 km之间速度层合并为一层,其值为6.14 km/s,进而使速度模型更加简单。25~30 km处速度值低于初始模型速度约0.07 km/s,其下方30~35 km之间速度值几乎无变化。35 km之下速度变化不大,由原来的6.68 km/s降为6.61 km/s。
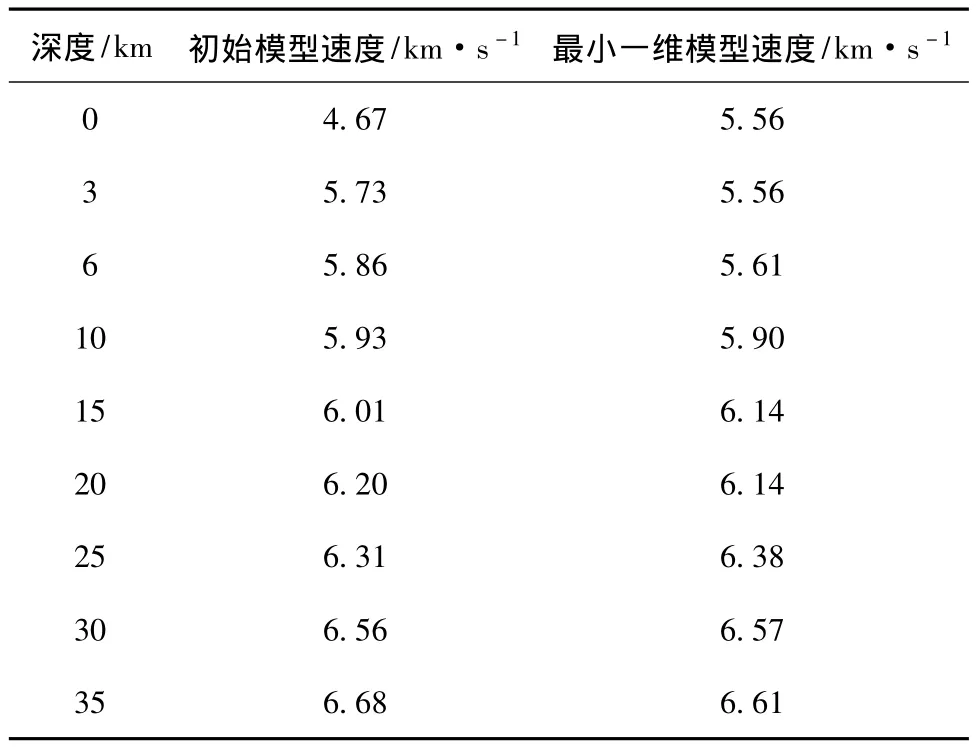
表1 初始模型与最小一维模型速度值对比Tab.1 The contrast between the initial velocitymodel and minimum 1D velocity model
为检验一维速度模型的稳定性,我们使用了3种速度模型进行反演 (图7中虚线),3种速度模型分别高于、等于和低于最小一维速度模型1 km/s。测试结果 (图7中实线)表明:3种模型最终都收敛到同一个模型上,浅层0~10 km速度模型与最小一维速度模型相差约0.2 km/s,速度约束能力稍差,可能是浅层地壳速度变化的影响被台站校正所补偿;而10~30 km之间,地震射线较为密集,对速度约束能力较强,其速度收敛于最小一维速度模型。30 km之下,稀疏的地震数据对速度约束能力有限,进而使得速度与最小一维速度模型之间出现0.1 km/s的速度差异。
2.3 台站校正
本文将浅层介质横向不均匀性对反演结果的影响归结到台站校正项上,以便减小一维速度模型产生的误差。台站校正值反映了速度模型与真实速度模型之间的差异,台站校正值的负、正分别对应台站布设地区速度异常的高低 (Carla et al.,2003)。获得的台站校正范围为 -1.10~0.46 s(表2),不同的台站校正值表征出龙门山断裂带南段地表速度结构的横向不均匀性,该区速度异常与地表地质构造有一定的对应关系。校正值为负的5个台站 (图1中紫色三角)皆位于龙门山断裂带西北侧的青藏高原上,表明青藏高原近地表速度为高速异常。校正值为正的台站(图1中蓝色三角)位于龙门山断裂带及其东南侧的四川盆地上,表明其为低速异常,这与三维地震层析成像研究结果相一致 (Lei et al.,2009;Huang et al.,2002;Pei et al.,2010)。
2.4 地震定位
结合最小一维速度模型及台站校正,使用VELEST程序中“单地震模式”对选取的龙门山地区587个地震进行了绝对定位。在“单地震模式”中,走时、台站坐标、台站校正及速度场均已知,仅对震源参数进行反演求解。由重定位前后地震分布图 (图8)可以看出,重定位后地震呈现出更加明显的北东向条带分布,其中汶川余震序列多集中在龙门山中央断裂及后山断裂附近,芦山余震序列位于龙门山前山断裂南段的双石—大川断裂两侧,其余震序列北段地震分布范围较宽,而南段明显变窄。相比于初始震源分布,重定位后震源深度整体变浅,平均震源深度为15.67 km,其中10~22 km深度范围内的地震达到93%以上,且在14 km附近最为集中,地震优势分布非常明显。图9给出了芦山震区相互垂直的两个剖面上震源分布情况。在沿主破裂方向的A-AA剖面上,剖面10~20 km之间地震数量较少且分布较浅,20~40 km之间地震较多。B-BB剖面上,芦山地震序列呈明显的条带状并向北西倾斜,14 km以下发震层倾角约40°±2°,与刘杰等 (2013)、王卫民等 (2013)获得的芦山主震震源机制解相近,浅部发震层倾角较大 (约68°±2°)。倾向北西的地震带上方出现一条反冲地震带,两地震带呈“y”型分布。
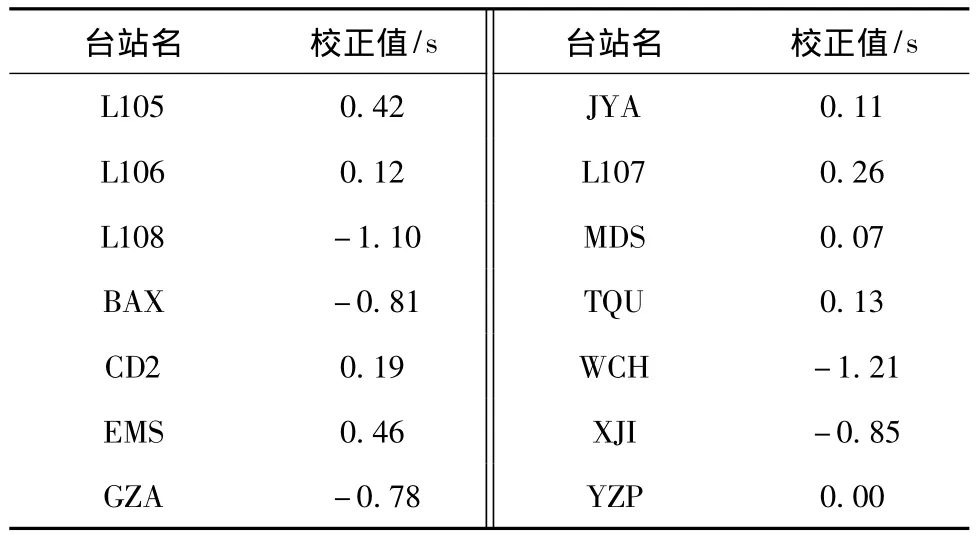
表2 台站校正值Tab.2 Station correction value
为了进一步检验最小一维模型能否改进地震定位质量,我们分别根据最小一维速度模型与模型6对龙门山断裂带南段的地震进行重定位。对重定位后的走时均方根残差 (RMS)进行对比 (图10)发现,模型6重定位后获得的地震走时均方根残差(RMS)位于0.08~0.62 s之间,峰值位于0.30 s及0.40 s附近,而最小一维速度模型重定位后地震走时均方根残差 (RMS)整体向0 s偏移,RMS主要分布在0.00~0.40 s之间,且在0.12 s附近最为集中。可以看出最小一维速度模型定位精度显著提高,表明Kissling方法获得的最小一维模型与真实模型更为接近,能够显著提高地震定位的质量。
3 结论
使用最小一维速度模型可以减轻横向速度不均匀性及场地效应对地震定位产生的影响,从而有效地提高地震重定位的精度。本研究利用P波震相数据反演龙门山断裂带南段一维速度模型及台站校正:根据先验信息建立了12种初始速度模型,在初始速度模型中插入新的界面以便拟合速度变化,在反演过程中将速度相近的相邻速度层或分辨率较差的薄层合并,最终获得较为稳定的速度模型,最后根据地震走时均方根残差 (RMS)对12种模型进行对比,选择走时均方根残差(RMS)最小的速度模型作为最小一维速度模型。
反演得到的台站校正值反映了龙门山断裂带南段近地表速度的横向不均匀性,青藏高原上负的台站校正值表明青藏高原近地表为高速异常,与该区彭灌高速杂岩体及宝兴高速杂岩体相对应,而四川盆地正的台站校正值表明四川盆地第四纪沉积表现为低速异常。由于台站校正的补偿,浅层速度约束能力不明显,因此需结合台站校正进行地震定位研究。
地震重定位结果显示,地震主要分布在倾角约40°±2°的北西倾斜的地震面上,与宝兴杂岩下方的滑脱带延伸趋势一致,而浅层出现的大倾角破裂可能阻碍了断层的逆冲滑动,使得浅层地震明显减少。此外,地震带上方出现一条反冲地震带,可能是地震发生时介质为了调节逆冲过程所受的阻力,进而使得宝兴杂岩上方的岩层产生了反冲运动。
郑秀芬老师及国家地震科学数据共享中心为本研究提供了数据支持,所有图件均使用GMT绘制,在此一并表示感谢。
黄玉婷.2012.汶川8.0级地震震源精确定位及震源机制研究[D].四川:成都理工大学.
黄媛,吴建平,张天中,等.2008.汶川8.0级大地震及其余震序列重定位研究[J].中国科学(D 辑),38(10):1242 -1249.
刘博研,史保平,雷建设.2013.汶川地震对芦山地震及周边断层发震概率的影响[J].地震学报,35(5):642 -651.
刘杰,易桂喜,张致伟,等.2013.2013年4月20日四川芦山M7.0级地震介绍[J].地球物理学报,56(4):1404 -1406.
滕吉文,白登海,杨辉,等.2008.汶川地震发生的深层过程和动力学响应[J].地球物理学报,51(5):1385 -1402.
王卫民,郝金来,姚振兴.2013.2013年4月20日四川芦山地震震源破裂过程反演初步结果[J].地球物理学报,56(4):1412-1417.
吴建平,黄媛,张天中,等.2009.汶川MS8.0级地震余震分布及周边区域P波三维速度结构研究[J].地球物理学报,52(2):320-328.
徐锡伟.2009.5·12汶川8.0级地震地表破裂图集[M].北京:地震出版社,108.
杨智娴,陈运泰,郑月军,等.2003.双差地震定位法在我国中西部地区地震精确定位中的应用[J].中国科学(D辑),33(B04):129-134.
张培震,徐锡伟,闻学泽.2008.2008年汶川8.0级地震发震断裂的滑动速率、复发周期和构造成因[J].地球物理学报,51(4):1066-1073.
赵珠,范军,郑斯华,等.1997.龙门山断裂带地壳速度结构和震源位置的精确修定[J].地震学报,19(6):615 -622.
赵珠,张润生.1987.四川地区地壳上地幔速度结构的初步研究[J].地震学报,9(2):154 -166.
郑秀芬,欧阳飚,张东宁,等.2009.“国家数字测震台网数据备份中心”技术系统建设及其对汶川大地震研究的数据支撑[J].地球物理学报,52(5):1412 -1417.
Carla M.,Giuseppe D.G.,Stefano G..2003.Minimum 1-D Velocity Model in Southeastern Sicily(Italy)from Local Earthquake Data:an Improvement in Location Accuracy[J].J.Seismol,7(4):469-478.
Clark M.K.,Royden L.H..2000.Topographic Ooze:Building the Eastern Margin of Tibet by Lower Crustal Flow[J].Geology,28(8):703-706.
Crosson R.S..1976.Crustal Structure Modeling of Earthquake Data:1.Simultaneous Least Squares Estimation of Hypocenter and Velocity Parameters[J].J.Geophys.Res.,81(17):3036 -3046.
Eberhart P.D.,Michael A.J..1993.Three-dimensional Velocity Structure,Seismicity,and Fault Structure in the Parkfield Region,Central California[J].J.Geophys.Res.,98(B9):15737 - 15758.
Huang J.L.,Zhao D.P.,Zheng S.H..2002.Lithospheric Structure and its Relationship to Seismic and Volcanic Activity in Southwest China[J].J.Geophys.Res.,107(B10):2255.
Kissling E.,Ellsworth W.L.,Eberhart P.D.,et al..1994.Initial Reference Models in Local Earthquake Tomography[J].J.Geophys.Res.,99(B10):19635 -19646.
Kissling E.,Solarino S.,Cattaneo M..1995.Improved Seismic Velocity Reference Model from Local Earthquake Data in Northwestern Italy[J].Terra Nova,7(5):528 -534.
Klemperer S.L..2006.Crustal Flow in Tibet:A Review of Geophysical Evidence for the Physical State of Tibetan Lithosphere,in Channel Flow,Ductile Extrusion and Exhumation of Lower Mid-Crust in Continental Collision Zones,edited by M.P.Searle and R.D.Law [J].Geol.Soc.Spec.Publ.,268:39 -70.
Lee W.H.K.,Stewart S.W..1981.Principles and Applications of Microearthquake Networks[M].London:Academic Press,293.
Lei J.S.,Zhao D.P.,Su J.R.,et al..2009.Fine Seismic Structure Under the Longmenshan Fault Zone and the Mechanism of the Large Wenchuan Earthquake[J].Chinese J.Geophys.,52(1):112-119.
Michael A.J..1988.Effects of Three-dimensional Velocity Structure on the Seismicity of the 1984 Morgan Hill,California,Aftershock Sequence[J].Bull.Seismol.Soc.Am.,78(3):1199 -1221.
Parsons T.,Ji C.,Kirby E..2008.Stress Changes from the 2008 Wenchuan Earthquake and Increased Hazard in the Sichuan Basin[J].Nature,454:509 -510.
Pei S.P.,Su J.R.,Zhang H.J.,et al..2010.Three-dimensional Seismic Velocity Structure Across the 2008 Wenchuan MS8.0 earthquake,Sichuan,China[J].Tectonophysics,491(4):211 - 217.
Royden L.H.,Burchfiel B.C.,Vander H.R.D..2008.The Geological Evolution of the Tibetan Plateau[J].Science,321:1054 - 1058.
Royden L.H..1996.Coupling and Decoupling of Crust and Mantle in Convergent Orogens:Implications for Strain Partitioning in the Crust[J].J.Geophys.Res.,101(17):679 -17,705.
Thurber C.H..1985.Nonlinear Earthquake Location.Theory and Examples[J].Bull.Seismol.Soc.Am.,75(3):779 -790.
Thurber C.H..1992.Hypocenter Velocity Structure Coupling in Local Earthquake Tomography[J].Phys.Earth planet Inter.,75(1):55 -62.
Vander H.R.D.,Spakman W..1989.Importance of the Reference Model in Linearized Tomography and Images of Subduction Below the Caribbean Plate[J].Geophys Res Lett,16(10):1093 - 1096.
Wang C.Y.,Han W.B.,Wu J.P.,et al..2007.Crustal Structure beneath the Eastern Margin of the Tibetan Plateau and its Tectonic Implications[J].J.Geophys.Res.,112(B7):1 - 21.

