胶带输送机输送带的动力学模型及分析方法

张晓君

（同煤集团云冈矿，山西 大同 037017）

1 对输送带进行动力学研究的重要性

皮带是皮带输送机的核心部分，起着承载物料和提供牵引力的作用，在整个皮带输送机中传送带占成本的百分之三十到百分之五十之间。大部分传送带受到破坏是由于大块的、尖的物料冲击引起的输送带面磨损和边缘的磨损。皮带能够反映皮带输送机最基本的特征。随着煤矿投产规模的不断扩大，运量大、距离长、速度快的大型胶带输送机已逐渐成为胶带输送机发展的主流。

在分析胶带输送机的动态性能和系统响应时，首先需要建立皮带输送机系统的动态模型，同时也需要测定传送带及其特征参数，然后建立输送带动力学模型。输送带力学模型建立的是否适当，确定参数是否恰当，不仅会影响输送系统动态分析的准确性，还会直接影响到动态分析的精度和可靠性。所以对输送带进行动力学的研究很有必要［1］。

2 输送带的动力学模型

2.1 输送带动力学特性

输送带的变形量与很多因素有关，如加载的大小、频率、时间、材料特性、环境温度和加载历史等。因为在生产输送带时，受橡胶特性的影响，输送带的动力特性十分复杂。主要表现在以下方面［2］。

1）输送带和一般的弹性材料是不同的，他的应力－应变关系是非线性特性曲线，当他收到缓慢的拉力发生变形时，输送带的变形与所受到的拉力，与胡克定律不完全相符，其受力的非线性特点如下页图1－1所示。

2）输送带的应变不会迅速增大，会有一定的滞后缓慢增大；当卸载后，应变不会立即恢复到原来的位置，卸载应力－应变曲线需要经过时间历程才能与加载应力－应变曲线重合，如下页图1－2所示。

3）输送带具有蠕变特性，对输送带加载时，应力迅速增加，而输送带不会迅速伸长，他将会随着时间的推移逐渐增加，经过一段时间才会到达稳定值，如下页图1－3所示。即输送带的阶跃响应，应力和应变的变化规律是相同的，但是应变相对于应力要滞后一些，最终都达到稳定状态。

4）输送带具有松弛特性，对输送带施加一定的载荷，使输送带达到一定的伸长，并保持伸长量不变时，经过一段时间之后，载荷将缓慢减小，最后数值趋于稳定，见下页图1－4。

5）输送带的动态特性与拉力的作用频率有很大的关系。在力学性能方面，输送带具有很大的黏性，输送带的动态特性如下页图1－5所示。在实际中，无法对皮带输送机缓慢地施加载荷来进行测量，所以在研究输送带应力和应变的变化模型时，需要考虑他的动态性［3］。

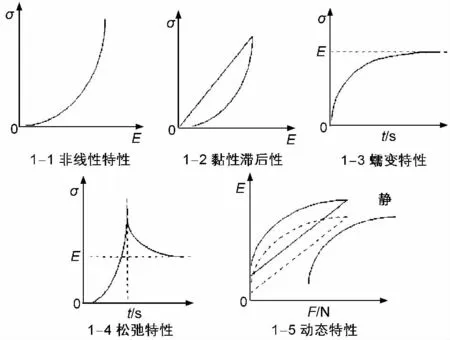
图1 皮带的传动特性

关于胶带输送机输送带的黏弹性的研究已经十分广泛，但理论对于小型胶带输送机的影响甚微，对于距离长、带速高、运量大的大型胶带输送机的影响将是非常重要的，在输送带的设计中必须考虑输送带的黏弹特性。

2.2 输送带动力学特性的数学模型

输送带具有很强的黏弹特性，所以建立输送带的动力学模型的时候应该采用黏弹性模型［4］。研究黏弹性体可以认为是流体力学的研究范围之内，根据胡克定律弹性的数学模型公式为：

式中：σ为应力；ε为应变；E为弹性模量，Pa。

黏性是流体的主要特性，图2－2 为阻尼器模型，表达方式为：

式中：η为黏性系数，Pa·s。

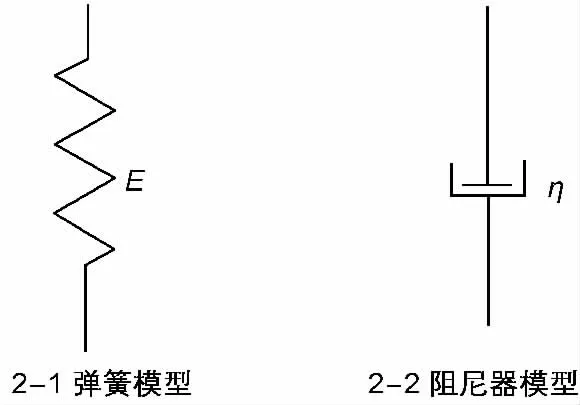
图2 弹簧模型和阻尼器模型

复杂的数学模型可以对实际情况的动力学描述更加具体和准确，但是存在一些问题，如：复杂的数学模型中参数较多，而这些参数难以全部准确的求解；复杂的数学系统求解起来非常困难，甚至有的无法求解。这就要求在选择数学模型时综合考虑。对于输送带的动力学模型来说，国内外专家做了很多的研究，也建立了很多数学模型，最有名的有以下几种，见图3所示。

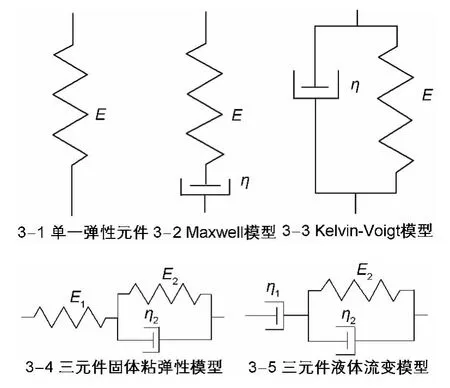
图3 输送带动力特性模型

以图3中E，E1，E2为元件的弹性模量；η，η1，η2为元件的黏性系数。

以上数学模型的数学方程式为：

胡克弹性模型：

Maxwell数学模型：

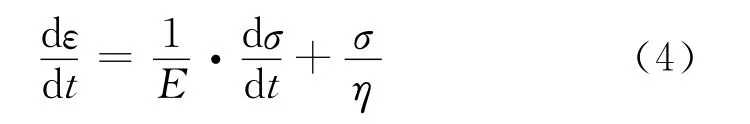
Kelvin－Voigt数学模型：

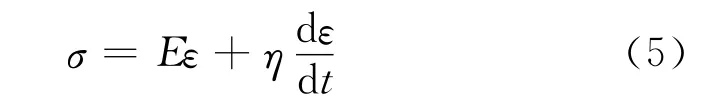
三元件固体黏的弹性模型：

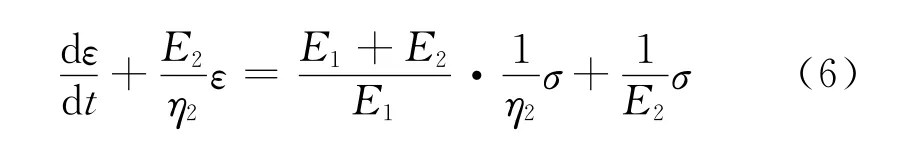
三元件液体流变的数学模型：

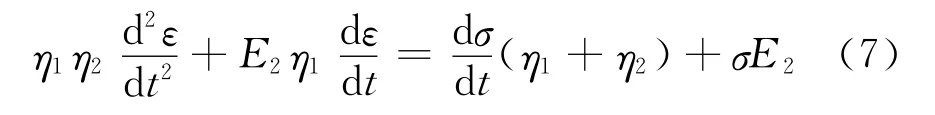
式（3）～式（7）数学模型是输送带动力学特性研究中比较常见的模型。下面详细分析提到的数学模型，以选择合适的输送带动力学数学模型。

1）胡克模型。胡克模型是由一个弹簧组成的简单的模型，见图3－1。

当该模型收到一个恒定的应力的时候，即σ＝σ0H（t）时，可以计算出应变与时间的关系：

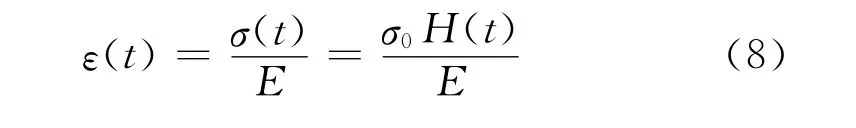
当该模型发生恒定的应变时，可计算出应力与时间之间的关系：

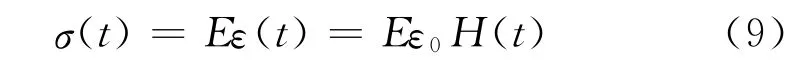
综合式（8）、式（9）可以求得该模型的蠕变模量F（t）和松弛模量E（t）分别为：

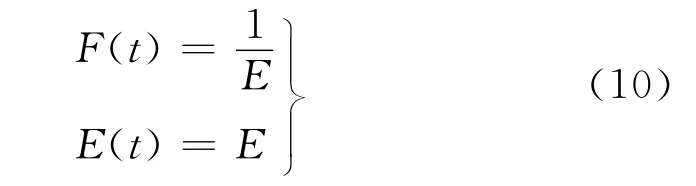
2）Maxwell模型。对该模型施加一个恒定的应力时会产生应变，保持这个应变值不变，即＝0时，可得：

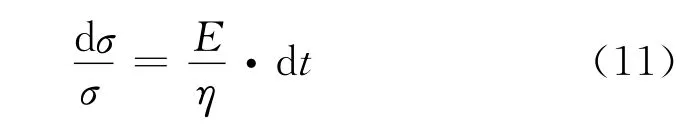
在最初的条件下，即t＝0，σ＝σ0的情况下，可以计算出应力与时间的关系为：

式（12）的两边同除以ε0，可以得到：

由此可以体现出该模型的松弛特性［5］。

3）Kelvin－Voigt模型。Kelvin模型见上页图3－3。弹簧的应力－应变关系为：

阻尼器的应力－应变关系为：

它们和总的应力σ、总的应变ε的关系为

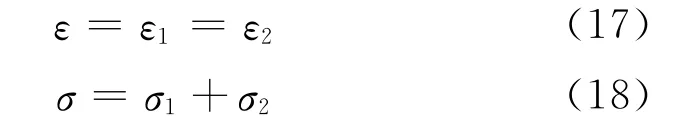
当该模型收到恒定的应力时，即σ＝σ0时，通过解一阶的微分方程，可得：

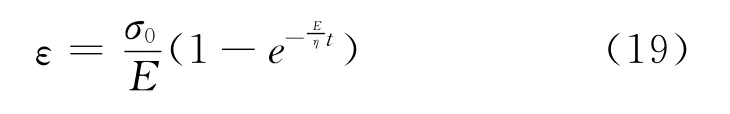
通过以上的分析可以看出该模型具有蠕变性，也就是说应力需经一段时间后才能达到一个稳定值，接近于。

4）三元固体模型。该模型是由两个弹性的元件以及一个黏性的元件串并联组而组成的模型，见上页图3－4。

当该模型收到一个恒定的应力时，即σ＝σ0H（t）时，可以计算出应变与时间之间的关系为：

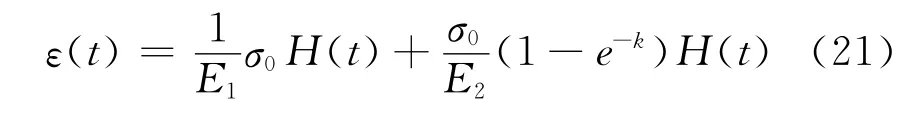
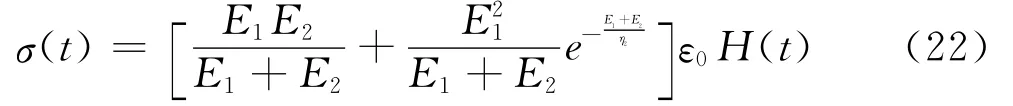
通过以上的计算可以得出该模型蠕变模量和松弛模量分别是：

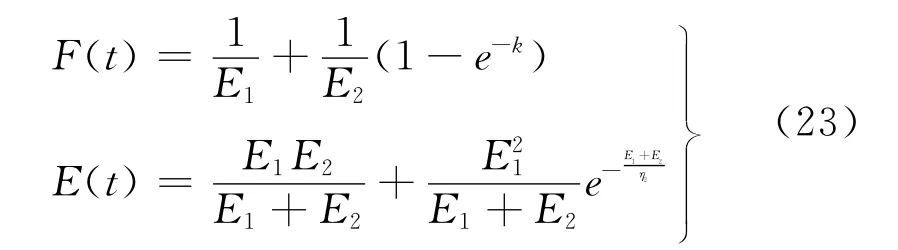
经过以上的计算，对不同输送带数学模型进行了分析，可以得出以下结论：Maxwell模型的蠕变呈线性特性，他的应力和拉伸应力松弛模量衰减形式是指数型的，所以这个模型也不能正确的描述输送机在运行时的动态特性；三元件固体弹性体元件以及其他四元件模型虽然蠕变特性和松弛特性比较好，也可以基本反映出输送带在运动时的动力学特性，但是这个模型的参数太多，模型复杂，计算量太大，也不适合用来描述输送带的动态特性。Kelvin模型更实用，在输送带动态性能的分析中，松弛特性的影响不是很大，因为输送带的自动张紧装置可以补偿皮带的松弛，并且对输送机的动态性能的研究，主要是起动和制动阶段的，这两个阶段皮带的松弛不大，Kelvin模型的参数便于测量，所以，该模型更为实用［6］。

3 结语

本文主要分析了对输送带进行动力力学研究的重要性，通过分析输送带的动力力学特性，建立输送带动力力学特性的数学模型，通过对比分析胡克模型、Maxwell模型、Kelvin－Voigt模型以及三元固体模型，参考各院校以及公司对输送机研究的情况，为了充分反映输送带在运行中的黏弹特性，得出采用Kelvin－Voigt模型来对输送带的动力学特性进行分析更具合理性和可行性。

［1］刘英林，王彦凤.输送带应力波传播速度［J］.太原理工大学学报，1999（7）：407－409.

［2］吴东平.一种新型胶带输送机张紧装置［J］.煤矿机电，2004（5）：75－78.

［3］刘绪玉.YzL－100型皮带机液压自动张紧装置的推广应用［J］.煤矿现代化，2003（6）：27－295.

［4］智立甫.基于Matlab的智能控制系统仿真研究［J］.河北农业大学，2004（6）：43－45.

［5］王春行.液压控制系统［M］.北京：机械工业出版社，2002.

［6］王显正.控制理论基础［M］.北京：科学出版社，2003.