块为三角形的简单图的最小Hosoya指数

张深林

（福建江夏学院数理教研部，福建福州，350108）

块为三角形的简单图的最小Hosoya指数

张深林

（福建江夏学院数理教研部，福建福州，350108）

一个图G的Hosoya指数是指图G中所有匹配的计数。用ζ表示块为三角形的简单连通图的集合，Gr∈ζ是ζ中块数为r的图，Wr∈ζ是ζ中直径为2，块数为r的图。利用边收缩法和数学归纳法可证Wr是Gr∈ζ中Hosoya指数最小的图。该结论在连通分支数大于1的图中也是成立的。

匹配；Hosoya指数；块

一、引言

Hosoya指数由日本化学家Hosoya[1]于1971年首次提出，它被看作是研究分子的物理特性和化学特性的一个重要指标，与分子的熔点、沸点、熵[2][3]都有密切关系。匹配是组合图论中的重要分支，Hosoya指出了图的匹配数作为拓扑指数在化学上的作用，并以此来描述饱和碳氢化合物的热力学性质。因此，确定一个图的最大或最小Hosoya指数是非常有意义的。

二、预备知识与主要定义

除特别说明外，本文假设G=(V，E)是简单连通图。设e=(u，v)是G的一条边（方便起见，有时也记为e=uv），G-u-v表示G中删去顶点u与v得到的顶点导出子图，G-e表示G中删去边e得到的G的边导出子图。图G的一个边子集M称为一个匹配（matching），如果G中的每个顶点与M中的至多一条边相关联；M称为G的一个完美匹配（perfect matching），如果G中的每个顶点恰好与M中的一条边相关联。记m(G，j)为G中含j条边的匹配的数目，习惯上总假定G的零匹配为1，即m(G， 0)=1，于是m(G，1)为图G的边数；而当n为偶数时，m(G,)则为G的完美匹配的数目。用Z(G)表示图G中所有匹配的数目，即Z(G)=m(G，0)+m(G，1)+…m(G，），图G中所有匹配的数目也称为Hosoya指数。

图G=(V，E)的顶点v称为割点，如果E可划分为两个非空子集E1和E2，使得G[E1]和G[E2]恰有一个公共顶点v。没有割点的连通图称为块。若图G的子图B是块，且G中没有真包含B的子图也是块，则称B是G的块[4]。

用ζ表示块为三角形的简单连通图的集合，Gr∈ζ是ζ中块数为r的图，Wr∈ζ是ζ中直径为2，块数为r的图，在一些地方也被称为风车图[4][5]（windmill graph）。图1给出了r=1，2，3，4的所有Gr∈ζ图。其中的a，b，c，e为r≤4的Wr。

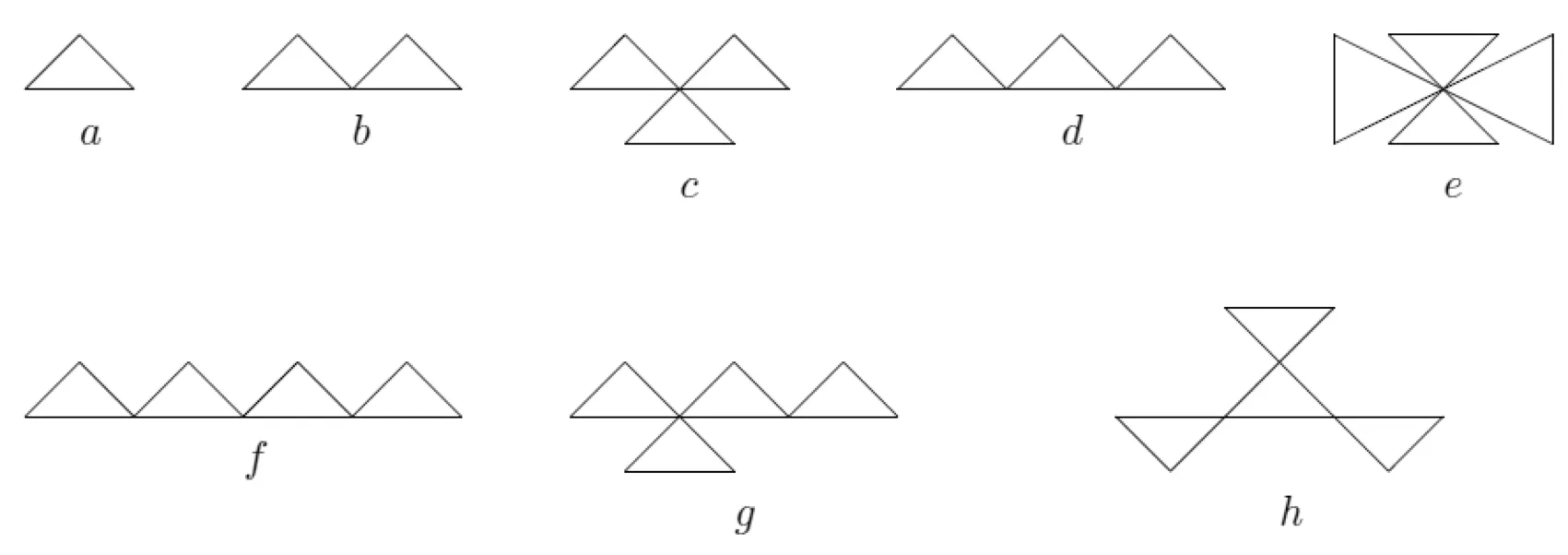
图1

在Gr∈ζ的块中，我们称恰有2个2度点的三角形为第一类三角形，数目为s1；恰有1个2度点的三角形为第二类三角形，数目为s2；有0个2度点的三角形为第三类三角形，数目为s3。显然

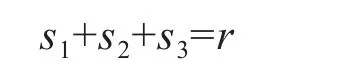
设顶点c∈V(Gr)，则以c为顶点的块三角形称为c关联的三角形。

三、 有关的引理

下面介绍与本文有关的引理。

引理3．1[6]设G是一个图，e=(u，v)是G的一条边，则

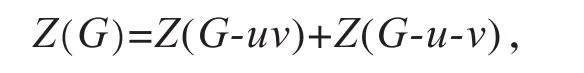
其中G-uv和G-u-v分别表示G中删去边e及删去顶点u与v的边导出子图与顶点导出子图。引理3．2[6]设v是图G的一个顶点，NG(v)表示v的邻点集，则

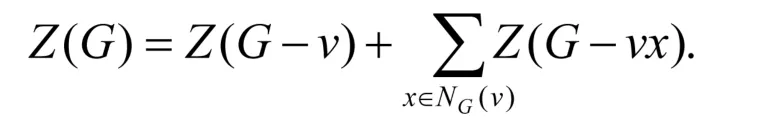
引理3．3[6]设图G有分支G1，G2，…，Gk，则

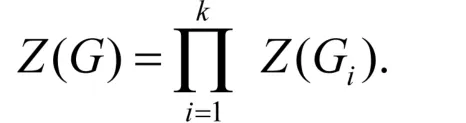
引理3．4[6]Cn表示有n个顶点的圈，Pn表示有n个顶点的路，Fn表示第n个斐波那契数（Fibonacci number），则

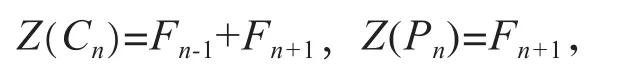
引理3．5[7]设Gr∈ζ是满足s3=0的简单图，从Gr图中的每个三角形都删去一个2度的顶点后得到的图记为Tr+1，且d1，d2，…，dr+1是图Tr+1的顶点的度序列，则

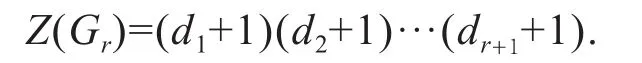
引理3．6[7]设G是有n个顶点的简单图，a是G的一个顶点。构造一个n+2个顶点的新图G'，使得G'的顶点集为V(G)=V(G')∪{x，y}，边集为E(G')=E(G)∪{ax，ay，xy}，其中x，y∈/V(G)，则

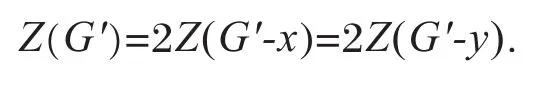
四、主要定理与结论

引理4．1 设Wr∈ζ是如上定义的简单图，则

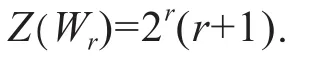
证明 因为Wr∈ζ也是满足s3=0的图，由引理3．5可知，Wr所对应的度序列为d1=d2=…=dr=1，dr+1=r，从而Z(Wr)=2r(r+1)．

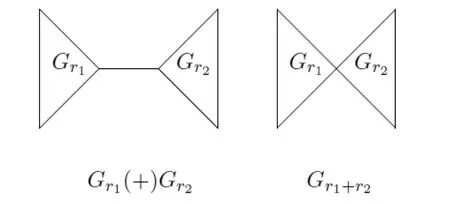
图2

引理4．2 用Gr1(+)Gr2表示用一条边连接Gr1和Gr2的某一顶点所成的图，Gr1，Gr2∈ζ，用Gr1+r2表示把Gr1(+)Gr2中唯一不在三角形块中的边收缩成连接Gr1，Gr2的公共顶点的图（如图2所示），则

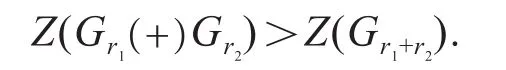
证明 显然，Gr1+r2的匹配都是Gr1(+)Gr2的匹配，反之则不然。

定理4．1 假设Gr∈ζ，r∈N+，则

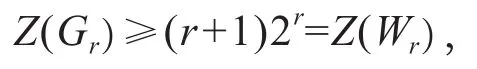
等号成立当且仅当Gr=Wr

证明 设Gr∈ζ，对块数r做数学归纳法。

（1）当r=1，2时，容易验证命题成立。现在假设命题对于r≤m成立，现考虑当r=m+1时。

（2）当r=m+1时，若Gr中的块都是第一类三角形，由引理4．1，命题成立。

若Gr中的块不全是第一类三角形，则必存在第二类或第三类三角形。任意选取图Gr的某一个非第一类三角形，考虑它的非2度顶点所联接的三角形是否第一类三角形，重复这个过程，直到找到这个第一类三角形为止（因为块数是有限的，所以寻找第一类三角形的过程也是有限的）。接着，考虑该第一类三角形的非2度顶点所关联的三角形，是否除了一个非第一类三角形外，其余都是第一类三角形，如果不是，则重复以上步骤，直到找到为止。则Gr中必存在一点c，除了关联一个非第一类三角形外，其余关联的三角形都是第一类三角形。设该点上关联p(1≤p≤r－2)个第一类三角形，分别是△1，△2，…，△p，记Gr-p=Gr－△1－△2－…－△p。由引理3．6及归纳假设可得，

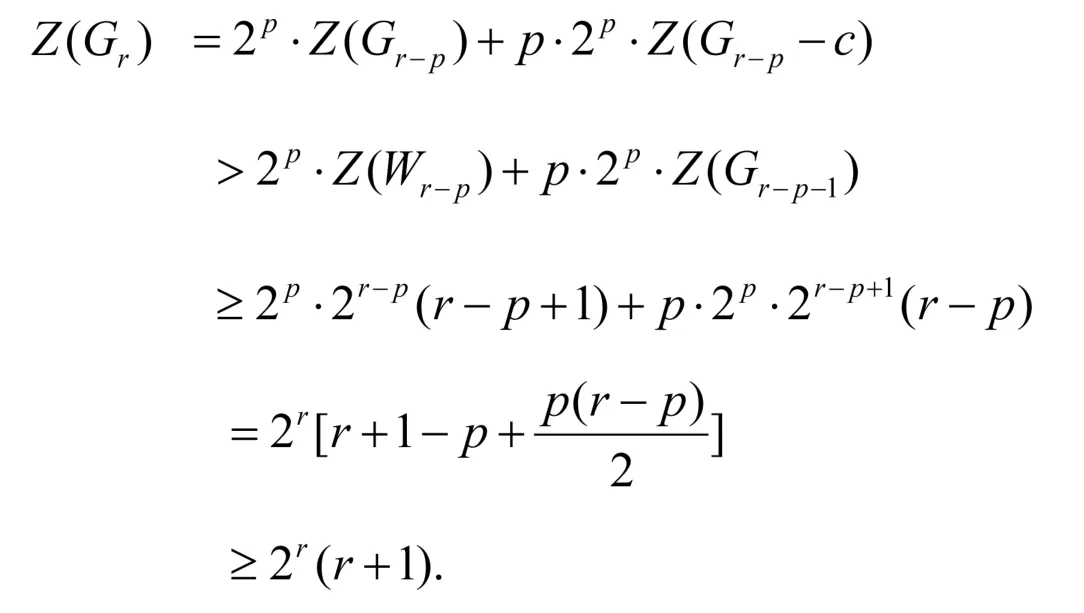
即命题对于r=m+1也成立。

综上所述，命题对于一切正整数都成立。

定理4．2 设1≤r1≤r2，则

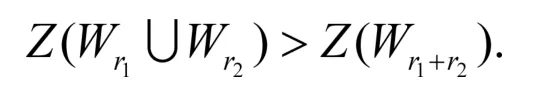
证明

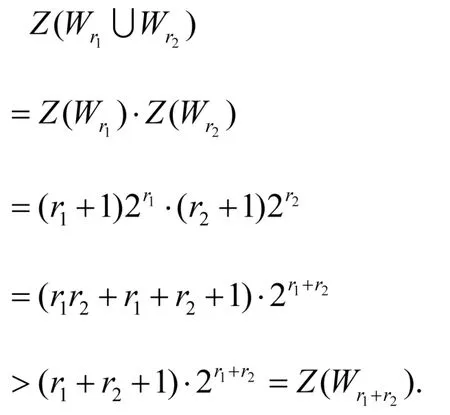
应用上述引理和定理，可以得到更一般的结果。

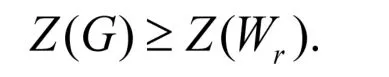
[1] Hosoya H．Topolpgical index,a newly proposed quantity charaterizing the topological nature of structural isomers of saturated hydrocarbons[M]．Bull Chem Soc Jpn,1971,44:2332-2339．

[2] Gutmani,Polanskyor．Mathematical concepts in chemistry[M]．Berlin:Spring,1986．

[3] Merrifield R．E．,Simmons H．E．,Topological methods in chemistry[M]．New York:Wiley,1989．

[4] 张先迪,李正良,图论及其应用[M]．北京:高等教育出版社,2005:277．

[5] Gallian,J．A．"Dynamic Survey DS6:Graph Labeling．"Electronic J．Combinatorics[J]．DS6,1-58,Jan．3,2007．

[6] Godsil C．D．,Algebraic Combinatorics[M]．New York． Chapman and Hall,1993．

[7] 晏卫根,叶永南．一类运算图的匹配数[J]．中国科学,2006,(9):1014-1022．

（责任编辑 王魏红）

Smallest Hosoya Index in Triangle-Block Graphs

ZHANG Shen-lin
(Department of Mathematics and Physics,Fujian Jiangxia University,Fuzhou,350108,China)

The Hosoya index of a graph G is defined as the number of matching in the graph G. Denoteζas the set of simple connected graph with triangle blocks. Wr∈ζis a graph consisting of r blocks. Wr∈ζis a graph consisting of r blocks and with diameter of 2.By using the method of edge contraction and mathematical induction, the paper proves that Wris the graph with the minimum Hosoya index in Gr∈ζ.This statement is also valid for a graph with the number of connected component greater than 1.

matching;Hosoya index;block

0157.5

A

2095-2082（2015）06-0112-04

2015-06-24

张深林（1979—），女，福建闽清人，福建江夏学院数理教研部教师。