基于三维正演的音频大地电磁阻抗相位不变量校正技术

阮帅，张炯，孙远彬，王绪本＊

1 油气藏地质及开发工程国家重点实验室（成都理工大学），成都 610059

2 西安交通大学人居环境与建筑工程学院，西安 710054

3 贵州省地质矿产勘查开发局103地质大队，贵州铜仁 554300

1 引言

音频大地电磁法（以下简称AMT）在我国油气、矿产勘探领域广泛应用（何展翔等，2004）.由于使用的设备轻便、勘探成本低廉，相对于其他电磁法更适应在西部山区开展工作，但山区的剧变地形和地表不均匀性会给数据解释带来很多假象（徐利明和聂在平，2005；赵国泽等，2007）.

大量的二维数据正演模拟结果表明，视电阻率、阻抗相位及其旋转不变量不容易受静态效应的影响，因此可作为实际资料一、二维反演结果好坏的重要评价手段（陈小斌，2010；阮帅，2013；苗景春等，2013）.随着三维正反演技术近年来的迅猛发展，更复杂的模型的三维模拟变得可行（Mackie等，1993；Zhdanov和 Fang，1996；Siripunvaraporn等，2002；鲁来玉等，2003；沈金松，2003；汤井田等，2007，2008），大量正演结果表明三维的强静态效应也会造成阻抗相位的畸变.因此，和二维模式不同，复杂地形、地质条件下的三维阻抗相位及旋转不变量必须进行有效校正才能用于异常定性分析.

虽然近年来三维反演问题的研究进步飞速（Newman和 Alumbaugh，2000；Siripunvaraporn和Egbert，2001；胡祖志等，2006；汤井田等，2007），但研究对象仍基本为水平地形模型的合成数据或大尺度的缓地形工区数据.山区高密数据集的大地电磁三维反演问题及其成效评价仍鲜有研究.笔者认为，在目前AMT勘探领域的主流定量分析手段仍然是一、二维的情况下，如何有效避免低维反演技术的静位移假象仍是非常值得探讨的问题，这一研究课题的结果可用来评价三维反演效果.

本文基于相对成熟可靠的交错网格大地电磁三维有限差分正演，提出简单实用的实测资料阻抗相位不变量校正技术，所有研究基于实际的西南某地金伯利岩AMT勘探的真实地形和真实数据.实测数据的一、二维反演参数基于三维正演合成数据试验选取，以获得低维假设下最合理的反演结果，同时试图结合反演和校正阻抗相位不变量以提高地质解释可靠性.该项目是三维复杂地形、地表不均匀的地质条件下寻找三维地质目标体的典型案例.

2 工区概述及三维地电模型

我国西南山区地质现象复杂、地形起伏，大部分地区在AMT勘探尺度上（1000m左右探深）几乎没有固定的地层模式.本文讨论的测区地表多出露石冷水组（∈2s）白云岩，在缓坡地带有零星第四系松散堆积物，地表电阻率分布非常复杂，地形变化非常剧烈，1km2范围内的最大高差几乎达到200m，施工测线设计只能顺地形进行，且地下构造非常复杂、无固定走向（不利于二维反演），施工布置见图1.

图1 西南某工区高程及测线、测点布置图测线号在顶部标注；三角形为测点，右边数字为测点号.Fig.1 Elevation map with survey lines and sites of the project Line No.on top；site present as triangles，numbers right side are site name.

该区勘探目标为金伯利岩管道，实际施工测线距200m，测点距50m，由于地形和植被原因L10线无法施工，实测数据静态效应严重，野外数据初步反演结果出现很多零星异常，且同一测线、不同反演参数和反演方法的结果完全不一致，地质解释人员几乎无法根据实测数据和反演结果得到确切、可信的结论.

为寻找准确的金伯利低阻异常、避免三维复杂地质条件下由于不满足一、二维反演应用条件而造成的错误解释，并需将反演结果和实测资料进行互相验证.基于近年MT技术的应用经验，阻抗相位数据不容易受静态位移影响，是非常重要客观的定性参数.但地形剧变的AMT正演研究表明，两个极化方向的阻抗相位和其旋转不变量都被地形影响并无法从中有效提取深部电阻率异常.

为此，若能求出地形、不均匀体引起的阻抗相位不变量，然后把这一响应在实测阻抗相位不变量中扣除，则校正后的阻抗相位不变量即为仅包含深部地质体信息的数据.

3 基于三维正演的阻抗相位不变量校正技术

为探讨如何校正阻抗相位不变量，我们可以利用第2节的地形数据和该区钻井资料建立两个三维地形剧变模型，以探讨地形、地表不均匀对深部异常的影响.第一个模型（MB）为地形、地电背景模型，地表电阻率可填充为观测数据的高频视电阻率或浅层电阻率调查结果，深部电阻率可为均匀空间或典型钻井的分层模型；第二个模型（MA）为异常模型，是在MB背景模型的基础上设置一些低阻管道.

根据前期钻井资料，工区主要岩性自上而下依次为牛蹄塘组（∈1n）灰岩；明心寺组（∈1m）黑色页岩夹石英砂岩；清虚洞组（∈1q）白云质灰岩、白云岩及同生角砾岩；石冷水组（∈2s）白云岩等.白云岩厚度约300～500m，深部岩层的电阻率逐渐降低，电性分层大致为类Q型.目标体金伯利岩管道因破碎严重兼富含云母电阻率更低.所有钻井均无电阻率测井数据，实验室测量露头和岩心的电阻率差别巨大，很难获取典型岩石电阻率，针对上述情况，为了尽量获取最佳MB背景模型，只能选取测区比较典型、静态位移较小的测点进行TE模式数据一维反演，得到简化的背景电阻率分层（图2）.

图2 测点405视电阻率、阻抗相位曲线（a）及其TE模式一维Occam反演结果（b）图a中实线为Occam反演模型的正演响应；图b中阴影部分为猜测的简化电性分层.Fig.2 1－D Occam inversion results of sites 405with its′apparent resistivity and impedance phase curves（a）Apparent resistivity and impedance phase curves（resulting model response curve present as solid line）；（b）1－D Occam inversion model result（shadowed part present as layers simplified background layers）.

MB背景模型的地形和地表电阻率必须和实际工区一致，首先根据栅格化的地形数据建立三维网格，中心标高大于实际高程的网格单元均填充为空气.空气以下的第一层网格单元根据浅地表调查的电阻率分布填充（本项目地形复杂，并无地表电阻率分布数据，且高频10000～1000Hz段的数据质量非常差，故地表填充为均一值）.其他网格单元电阻率按一维分析结果填充（图2b）.这样得到的模型和实际工区的宏观电性大致相同，同时又保留了引起静态效应的剧变地形和浅层不均匀体（图3a、图4a）.

MA模型可在MB模型的基础上修改获取，在L04、L12两条测线位置增加两个垂直低阻管道，这两个管道向深部逐渐扩大，图3b、图4b分别显示了MA的三维网格在L04剖面和L12剖面上的二维网格，图5为这两个管道在海拔500m和0m的水平切面位置.

对两个模型在东南西北四个边界及深部底边界均使用1.5倍的放大因子等比扩展10个网格和10个空气网格.采用三维交错采样网格有限差分法（Mackieet al.，1993）对 MB和 MA两个模型均进行了1000～10Hz频带与实测数据频率表一样的30个频率的正演计算（因为实测数据大部分测点在10000～1000Hz频段质量较差），获取TE和TM模式的三维阻抗张量，并依此计算阻抗相位不变量.MB和MA模型的计算结果如图6所示.

计算结果表明无论深部有无低阻金伯利岩管道，MB和MA模型的阻抗相位不变量形态相似，基本和地形变化一致，L04线异常被地形响应完全掩盖、L12线有微弱显示（图6中黑实线框所示）若不扣除地形响应，很难直接使用实测数据的阻抗相位不变量判断深部是否存在低阻陡立管道.

若已知MB模型的响应，实测阻抗相位不变量的校正非常简单易行.若MB的阻抗相位不变量为PB，实测资料的同频阻抗相位不变量为PO，则简单地形校正公式为

计算结果的PC为校正后的阻抗相位不变量，它已经扣除了地形、地表不均匀性（此时MB的浅层网格需根据浅层电阻率调查或高频视电阻率填充）的三维大地电磁响应.

图3 三维模型的L4线剖面电阻率分布图（a）MB模型；（b）MA模型.Fig.3 Profile L4of two 3Dresistivity mesh grid slide（a）MB；（b）MA.

图4 三维模型的L12线剖面电阻率分布图（a）MB模型；（b）MA模型.Fig.4 Profile L12of two 3Dresistivity mesh grid slide（a）MB；（b）MA.

图5 MA模型不同海拔深度切片显示（a）海拔500m；（b）海拔0m.Fig.5 Two slice maps on different elevation of model MA（a）Elv.on 500m；（b）Elv.on 0m.

必须指出，由于实际地形建模和三维电阻率网格填充误差，仅在背景选择比较合适的时候PC才有一般阻抗相位的特性.当背景电阻率误差较大时，PC等于45°并不表示电阻率均匀，但较大的PC对应电阻率降低的趋势，反之对应电阻率升高.

图7为使用公式（1）对1000Hz，10Hz两个频率的阻抗相位不变量进行校正的结果，可以明显看出地形影响已经消除，异常位置准确.

若在实测数据中应用此技术需事先编辑数据，因为存在干扰，校正前必须对阻抗相位不变量做第一象限变换、剔除跳点和平滑插值等操作.测区实际资料的阻抗相位不变量校正分析结果见第6节.

其他定性参数如二维偏离度、极化椭圆、电性主轴方向等平面图在三维地形剧变区域也会出现和阻抗相位类似情况，深部信息被地形、地表不均匀性影响，同样可以使用本文的思路对MB模型进行地形和地表不均匀性校正.因篇幅关系，这里不做赘述.

4 合成数据的校正阻抗相位不变量配合一维反演解释

大地电磁的一维反演技术已经非常成熟，但在二、三维性较严重（TE和TM模式曲线差别极大）的情况下难以应用，以Occam方法为例（Constable和Parket，1987），在做反演之前必须分析选取哪个模式的数据更好，并且电阻率曲线往往要进行平移（静校正）以避免出现“条带现象”.石油勘探的研究对象一般是沉积岩缓变地层，所以可以根据浅层电法勘探的结果（如TDEM）以高频为基准将视电阻率平移（何展翔等，2004），但这样做并不适合火山岩地形剧变地区（阮帅，2013），这些地区本来就可能存在大量陡立地层或电性体，它们在反演断面上的形态也应该是垂直条带（比如本文需要寻找的金伯利岩管道），在实际资料反演中无法确定哪些曲线需要平移，哪些不需要平移.因此，本文对所有数据都不做任何的平移式静位移校正，只选择横向分辨率最佳的模式做一维反演，获取尽量多的垂直条带，然后配合校正阻抗相位不变量排除假异常.

选取L04线进行一维Occam反演试验，输入数据分别为TE模式视电阻率和阻抗相位、TM模式视电阻率和阻抗相位、视电阻率和阻抗相位旋转不变量，结果分别如图8—10所示，比较图8、9和10，TM模式数据的一维结果对低阻管道更敏感，同时更容易受地形影响，在真实异常右边又出现了一条假条带；TE模式横向更不灵敏；不变量的结果则是二者的折中.

图11是MA模型TM模式一维Occam反演水平切片与10Hz校正阻抗相位不变量的套合.可以看出虽然一维反演切片显示出和地形趋势类似的低阻假象（一般在高地形出现），但结合等值线图可以排除这些假象，两者均显示低阻的地方与真实低阻管道位置一致.

通过以上的合成数据分析，可以得知，本测区的实际资料比较适合的一维反演解释方案如下：对TM模式数据剔除飞点，然后进行一维Occam反演，在其水平切片中寻找校正阻抗相位不变量较高，同时电阻率又较低的区域.

5 合成数据的校正阻抗相位不变量配合二维反演解释

避免静态位移假象更好的反演方法是二维带地形反演.以非线性共轭梯度法（以下简称NLCG）为例（Rodi和 Mackie，2001）：

其中，m为反演模型，F（m）为模型的二维正演响应，V为观测数据的协方差矩阵，d为观测数据，L为拉普拉斯算子的矩阵形式，λ为正则化因子，控制模型修正沿着光滑方向还是数据拟合方向，很多学者对这一反演方法进行了深入研究和改进，目前认为影响反演结果的主要因素有输入数据模式、反演网格、正则化因子等.

二维反演的输入数据以TE模式、TM模式或TE、TM模式联合会得到不同的结果，模型研究（苗景春等，2013）表明，TE模式的二维反演对“体”的倾向更好，而TM模式对地层的“形状”反应更好，联合TE和TM模式的数据分辨率更好，但损失倾向信息.本文对三种情况进行了大量试算比较，对于垂直陡立低阻脉，联合TE＋TM的结果更准确，因此用来反演金伯利岩更适合（试验过程从略）.

本工区测线为正南北方向，野外观测以正北为坐标系方向，输入数据可不做旋转直接反演，但研究表明在地下结构为三维体而非二维构造时输入数据旋转到最佳电性主轴（陈小斌，2010）的二维反演效果可能更佳.笔者对L12线进行不旋转和SWIFT旋转到最佳电性主轴的反演，结果如图12—15所示.

图6 两个模型的500Hz阻抗相位不变量平面图（a）模型 MB；（b）模型 MA.Fig.6 Impedance phase invariant slice maps on 500Hz frequency of two models（a）MB；（b）MA.

图7 MA模型阻抗相位不变量的两个频率简单地形校正结果（a）1000Hz；（b）10Hz.Fig.7 Corrected impedance phase invariant slice maps on two frequencies of MA

图8 L04线TM模式1DOccam反演结果Fig.8 1DTM mode Occam inversion of line L04

图9 L04线TE模式1DOccam反演结果Fig.9 1DTE mode Occam inversion of line L04

图10 L04线不变量1DOccam反演结果Fig.10 1DInvariant data Occam inversion of line L04

图11 MA模型海拔0m综合解释切片阴影图：TM模式1DOccam反演0m切片；等值线：10Hz校正阻抗相位不变量，粗线高值.Fig.11 Interpretation slice map on elv.at 0m Grid－map：slice map of 1DOccam inversion；contours：corrected impedance phase invariant，high value in bold line.

图12 L12线TE＋TM模式二维NLCG反演结果（不旋转；正则化因子0.3）Fig.12 NLCG TE＋TM data inversion results of line L12（no rotation；lambda as 0.3）

对比图12和图14，图13和图15，可见对于本项目所在的这种地形剧变条件，在不同的正则化因子下，L12测线不旋转的二维NLCG反演的效果更好（图12和图13）.在其他地形、地质条件下，若实际资料的测线不沿正南北，那么旋转方式可能为测线方位角（对应本文而言是0°，即不旋转）或最佳电性主轴.具体是否旋转，必须使用预设近似模型的合成数据试算确定.

通过大量试算，最终确定该区更适宜的二维NLCG反演的输入数据是：不经旋转、不经平移法静校正的TE＋TM模式数据；反演浅部网格深度取10Ωm趋肤深度的1／2比较合适（篇幅所限，大量试算结果从略）.

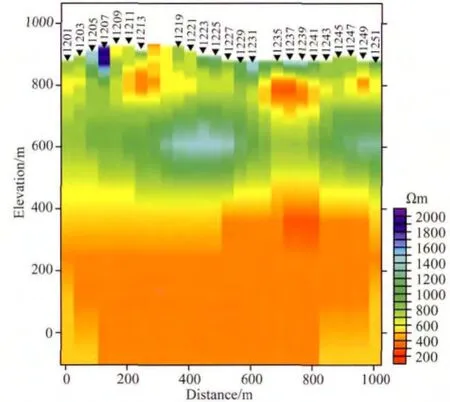
图13 L12线TE＋TM模式二维NLCG反演结果（不旋转；正则化因子3）Fig.13 NLCG TE＋TM data inversion results of line L12（no rotation；lambda as 3）

采取以上反演方案对MA合成数据的所有测线进行二维反演，其不同深度的水平切片如图16所示，相对于一维反演结果，二维NLCG反演能在测线方向压制地形影响.但是由于各条测线反演独立进行，无法对走向方向进行约束，切片图往往沿测线方向出现条带，易错误解释为南北向断层或岩性分界带.套合校正相位不变量10Hz切片等值线图后，深部100m切片的L06线北段低阻条带假象可避免，同时在L04线和L12线两个较大的非管状体切片形状的两个低阻带上，校正相位不变量有效的圈出了低阻金伯利岩的水平边界.

图14 L12线TE＋TM模式二维NLCG反演结果（旋转到最佳电性主轴；正则化因子0.3）Fig.14 NLCG TE＋TM data inversion results of line L12（swift rotation；lambda as 0.3）

图15 L12线TE＋TM模式二维NLCG反演结果（旋转到最佳电性主轴；正则化因子3）Fig.15 NLCG TE＋TM data inversion results of line L12（swift rotation；lambda as 3）

图16 MA模型的综合解释切片图（a）海拔500m切片；（b）拔100m切片；影像图为NLCG反演电阻率切片，等值线为10Hz校正阻抗相位不变量，粗线高值.Fig.16Interpretation slice maps（a）Elv.on 500m；（b）Elv.on 100m；grid－map：slice map of 2DNLCG inversion resistivity，contours：corrected impedance phase invariant，high value in bold line.

6 实测数据的综合解释

综合第3、4、5节的研究，实测数据应首先进行剔除飞点处理，然后使用D＋反演技术（Parker，1980）对TE、TM模式的视电阻率和阻抗相位进行圆滑插值.将圆滑插值后的阻抗相位不变量使用公式（1）扣除MB模型合成数据的同频响应（图17）.

图17的黑框标识处表明经相位不变量地形校正后，由高地形引起的高相位异常被有效去除，同时西南角的高相位圈闭面积也相应缩小，东南角的地层更趋向于稳定.疑似管状体的位置在北东向对角线上出现3个.为提高解释分辨率，套合电阻率反演结果切片时我们只绘制校正阻抗相位的高值（55°～60°）等值线.

一维反演采用第4节模式，二维反演采用第5节模式，因为这两种模式都是依据MA模型反复试算得到的较合理的反演模式，相对于其他方式，它们的结果可靠性应该更强.所有反演输入数据都根据D＋圆滑进行了飞点剔除.一维、二维反演水平切片和校正阻抗相位同频切片等值线的套合结果如图18和图19a所示.

图17 实测数据相位不变量500Hz水平切片（a）原始数据；（b）校正后数据；大于60°的奇异值已经剔除.Fig.17 Measured impedance phase invariant slice map on frequency 500Hz（a）Before correction；（b）After correction；Notice：values bigger than 60are removed.

图18 实测数据一维OCCAM反演综合解释切片（a）海拔500m；（b）海拔100m；影像图为电阻率切片，等值线为图17b，只绘制55～60°.Fig.18 Interpretation slice maps of measured data 1DOccam inversion（a）Elv.on 500m；（b）Elv.on 100m.grid－map：slice map of inversion resistivity；contours：equals Fig.17right only plot values from 55～60degrees.

图19 实测数据二维NLCG反演综合解释图（a）切片海拔300m，做图方式和图18相同；（b）L08剖面，不旋转，正则化因子3.Fig.19 Interpretation slice and profile maps of measured data 2DNLCG inversion（a）Elv.on 300m，same drawing scheme as Fig.18；（b）Profile L08，no rotation，lambda as 3.

图18的阻抗相位不变量高值区域显示低阻体主要位于东南部，主对角线上连续出现3个圈闭状高阻抗相位，这些圈闭在西北角并未出现，所以一维反演的西北部低阻异常是目标金伯利岩管道的可能性较小，这和图19a的二维反演电阻率深部切片揭示的地层关系一致.利用同时出现低电阻率、高校正阻抗相位的组合模式判断低阻体更可靠.

不仅如此，由于二维反演无东西向约束，在测区中心的高相位圈闭上（图19a）并没有显示出明显的低阻（相对于西南和东北角），但后期的钻井揭示该阻抗相位圈闭确实是深部金伯利岩管道的反映，而这一点在L08反演的剖面图上也有显示.因此校正阻抗相位不变量应该引起重视，即避免大量假异常，也有可能避免因为反演技术局限而丢失异常的情况.

依照这种先做三维背景模型MB和异常模型MA，以MB的三维正演得到的阻抗相位不变量为校正量进行校正，同时对MA的正演响应进行一维、二维反演的参数试验，确定最佳反演方案，反演电阻率水平深度切片和校正阻抗相位频率切片配合解释，寻找反演结果显示低阻、同时校正相位不变量显示高值圈闭的区域，获得比较可靠的解释结果，后期钻探验证已经得到证实.

7 结论

复杂地形、地质条件下，MT／AMT的实测阻抗相位不变量会受地形、地表不均匀性的影响，若根据实际地形和浅地表电阻率建立合适的背景模型（MB），基于三维正演进行阻抗相位校正能够扣除这些影响.

在MB的基础上可建立和工区地质体模式一致的假想模型MA，对MA的三维正演合成数据进行一、二维的反演试验，选择比较合理的反演方案，这一方案大部分情况下比较适合实测数据的反演.

不同反演技术得到的水平切片有不同的特点，一般一维反演切片有较多零星分布的假异常；二维反演能有效压制同测线上的假异常，但由于各测线做二维反演时互相无约束，在水平切片图上易产生测线方向的条带，只有三维反演才能有效压制各组数据独立反演引起的“数值差”，避免假圈闭和条带.

因此，所有一维、二维反演电阻率的水平切片图都应该配合校正阻抗相位不变量等值线进行解释，寻找二者的共同规律，在校正阻抗相位不变量和反演结果矛盾的地方，需要更细致的判断和分析（如图19a），避免丢掉有用的异常.

本文研究的解释方法可以推广到西部山前带油气勘探的低频MT数据解释.在三维反演技术普及性应用之前，这种方法可用来提高一、二维反演断面的地质解释准确性，在三维反演广泛应用之后，校正阻抗相位不变量也可用来进行三维反演结果的进一步评价.

致谢 感谢国家重大科学仪器设备开发专项基金对研究的大力支持，并特别感谢贵州省地质矿产勘查开发局103地质大队为本文的研究提供宝贵的实地数据和相关地质背景介绍.

Chen X B.2010.Effects of topography to magnetotelluric measured data and two dimensional inversion correction with topography（in Chinese）.／／China Geophysics 2010－26th Annual of CGS＆13th Academic Congress of SSC，325.

Constable C S，Parker R L.1987.Occam’s inversion：apractical algorithm for generating smooth models from electromagnetic sounding data.Geophysics，52（3）：289－300.

He Z X，Jia J D，Gou L.2004.The role of non－seismic techniques in exploration and development of oil and gas.Petroleum Exploration and Development（in Chinese），28（4）：70－72.

Hu Z Z，Hu X Y，He Z X.2006.Pseudo－three－dimensional magnetotelluric inversion using nonlinear conjugate gradients.Chinese J.Geophys.（in Chinese），49（4）：1126－1234.

Lu L Y，Zhang B X，Bao G X.2003.Modeling of three－dimensional magnetotelluric response for a linear earth.Chinese J.Geophys.（in Chinese），46（4）：568－575.

Mackie R L，Madden T R，Wannamaker P E.1993.Threedimensional magnetotelluric modeling using difference equations：Theory and comparisons to integral equation solutions.Geophysics，58（2）：215－226.

Miao J C，Ruan S，Zhang Y.2013.The application of the audio magnetotelluric sounding method to the precise interpretation of formal and reverse faults.Geophysical ＆ Geochemical Exploration （in Chinese），37（4）：681－686.

Newman G A，Alumbaugh D L.2000.Three－dimensional magnetotelluric inversion using non－linear conjugate gradients.Geophys.J.Int.，140（2）：410－424.

Parker R L.1980.The inverse problem of electromagnetic induction：Existence and construction of solutions based on incomplete data.J.Geophys.Res.，85（B8）：4421－4428.

Rodi W L，Mackie R L.2001.Nonlinear conjugate gradients algorithm for 2－D magnetotelluric inversion.Geophysics，66（1）：174－187.

Ruan S.2013.Discussion of static shift effect in practical AMT data inversion and interpretation（in Chinese）.／／China Geophysics 2013－29th annual of CGS.volume 24：631－632.

Shen J S.2003.Modeling of 3－D electromagnetic response in frequency domain by using staggered－grid finite difference method.Chinese J.Geophs.（in Chinese），46（2）：281－288.

Siripunvaraporn W，Egbert G.2001.An Efficient data－subspace inversion method for 2－D magnetotelluric data.Geophysics，65（3）：791－803.

Siripunvaraporn W，Egbert G，Lenbury Y.2002.Numerical accuracy of magnetotelluric modeling：a comparison of finite difference approximations.EarthPlanetsSpace，54（6）：721－725.

Tang J T，Ren Z Y，Hua X R.2007.The forward modelling and inversion in geophysical electromagnetic field.Progress in Geophysics（in Chinese），22（4）：1181－1194，doi：10.3969／j.issn.1004－2903.2007.04.025.

Tang J T，Luo W B，Liu C S.2008.Impulse response of seafloor hydrocarbon reservoir model.Chinese J.Geophys. （in Chinese），51（6）：1929－1935，doi：10.3321／j.issn：0001－5733.2008.06.036.

Xu L M，Nie Z P.2005.A fast forward algorithm for modelling vector electromagnetic scattering from buried dielectric objects.Chinese J.Geophys.（in Chinese），48（1）：209－215，doi：10.3321／j.issn：0001－5733.2005.01.028.

Zhao G Z，Chen X B，Tang J.2007.Advanced geo－electromagnetic methods in China.Progress in Geophysics （in Chinese），22（4）：1171－1180.

Zhdanov M S，Fang S.1996.Quasi－linear approximation in 3－D electromagnetic modeling.Geophysics，61（3）：646－665.

附中文参考文献

陈小斌.2010.地形对大地电磁观测资料的影响及二维带地形反演校正.／／中国地球物理2010——中国地球物理学会第二十六届年会、中国地震学会第十三次学术大会论文集，325.

何展翔，贾进斗，苟量.2004.非地震技术在油气勘探开发中的作用.石油勘探与开发，28（4）：70－72.

胡祖志，胡祥云，何展翔.2006.大地电磁非线性共轭梯度拟三维反演.地球物理学报，49（4）：1126－1234.

鲁来玉，张碧星，鲍光淑.2003.电阻率随位置线性变化时的三维大地电磁模拟.地球物理学报，46（4）：568－575.

苗景春，阮帅，张悦.2013.音频大地电磁测深法对正、逆断层的精细解释.物探与化探，37（4）：681－686.

阮帅.2013.AMT实测资料反演解释中的静态效应校正探讨.／／中国地球物理年会2013——第24分会场论文集，631－632.

沈金松.2003.用交错网格有限差分法计算三维频率域电磁响应.地球物理学报，46（2）：281－288.

汤井田，任政勇，化希瑞.2007.地球物理学中的电磁场正演与反演.地球物理学进展，22（4）：1181－1194，doi：10.3969／j.issn.1004－2903.2007.04.025.

汤井田，罗维斌，刘长生.2008.海底油气藏地质模型的冲激响应.地球物理学报，51（6）：1929－1935，doi：10.3321／j.issn：0001－5733.2008.06.036.

徐利明，聂在平.2005.埋地目标体矢量电磁散射的一种快速正演算法.地球物理学报，48（1）：209－215，doi：10.3321／j.issn：0001－5733.2005.01.028.

赵国泽，陈小斌，汤吉.2007.中国地球电磁法新进展和发展趋势.地球物理学进展，22（4）：1171－1180.