Impact Response of Stiffened Cylindrical Shells With/without Holes Based on Equivalent Model of Isogrid Structures

Qingsheng Yang,Shaochong Yang and Xiaohu Lin

Impact Response of Stiffened Cylindrical Shells With/without Holes Based on Equivalent Model of Isogrid Structures

Qingsheng Yang1,2,Shaochong Yang1,3and Xiaohu Lin4

An equivalent continuum model of an isogrid structure is utilized to analyze the impact response of isogrid structures and stiffened structures.The parameters of the equivalent model are determined,and the comparison between the equivalent continuous structure and the real grid structure are examined to validate the reliability of the equivalent model.Then,the impact responses of stiffened cylindrical shells with and without an elliptical hole are investigated by using the equivalent model of grid structures.For a different location and geometry of the elliptical hole,the deformation and load-bearing capacity of the grid-stiffened cylindrical shells are studied.The numerical results indicate that the present equivalent model can be applied effectively in simulation for the impact behavior of the grid and stiffened structures.This work provides a comprehensive understanding for the impact performance of the complicated stiffened cylindrical shells.

impact response,isogrid structures,equivalent model,stiffened cylinder,load-bearing capability.

1 Introduction

Lightweight grid-stiffened structures have a good energy absorption capacity,high load-bearing capacity,high specific strength and specific stiffness.These structures can be applied in many engineering fields,such as rocket interstages,payload adapters for spacecraft launchers,fuselage components for aerial vehicles,and components of the deployable space antennas[Vasiliev and Razin(2006);Bakhvalov,Petrokovsky,Polynovsky and Rasin(2009)].A review on the design and fabrication techniques of the grid structures has been given by Vasiliev,Baryninand Razin(2012,2001)Commercial and military aircraft usually undergo impact load in a specific situation,and may produce important safety issues.To understand the buckling phenomena and energy absorption capability of these structures under an impact load,many researchers have been devoting themselves to the study of impact performance.Han,Liu and Li(2004)presented an efficient hybrid numerical method for investigating transient response of crossply laminated axisymmet-ric cylinders subjected to an impact load.Adachi,Tomiyama,Araki and Yamaji(2008)found that the rib stiffness appropriately spaced in a cylinder can absorb a large amount of energy with a short crushing deformation.Morozov,Lopatin and Nesterov(2011)developed analytical and numerical methods to investigate the buckling behavior of anisogrid cylindrical shells under axial compression,transverse bending,pure bending and torsion.Totaro(2012)presented a refined analytical model for the local buckling modes of anisogrid cylindrical shells with regular triangular cells.Rahimi,Zandi and Rasouli(2013)showed that the rib stiffening of the shells could generally enhance the buckling load.

Moreover,the application of various stringers and rings in composite cylindrical shells and their impact behavior has been studied by Poorveis(2006).The effects of helical ribs and grid types on the buckling of thin-walled GFRP stiffened cylindrical shells under axial load were studied by Yazdani and Rahimi(2010).Using new development of multi-material formulation and fluid structure interaction developed in LSDYNA,Souli and Gabrys(2012)presented an experimental and numerical investigation of bird impact on radome.The dynamic response,energy absorption capability,deformation and failure of clamped aluminum face-sheet cylindrical sandwich shells with closed-cell aluminum foam cores were investigated by Jing,Xi,Wang and Zhao(2013)In particular,several examples of the local buckling model for periodic lattice structures without skin were presented by Fan,Jin and Fang(2009);Totaro(2013).

Furthermore,Rajendran and Grove(2002)presented detailed computational analyses investigating the ability of constitutive relationships to describe the response of a 99.5%pure alumina(AD995)subjected to a wide range of stress/strain loading states.Ghavami and Khedmati(2006)investigated the compression behavior and the dynamic response of stiffened plates.Oshiro and Alves(2007)simulated the responses of a cylindrical shell under axial impact to explore the correction procedure for scaled models.Zhang,Xue,Chen and Fang(2009)studied the deformation and failure mechanisms of lattice cylindrical shells under axial load by using the finite element software ABAQUS.Djeukou and von Estorff(2009)used a third-order shear deformation theory to deal the response of rectangular composite plates with low-velocity impact.Yazdani,Rahimi,Khatibi and Hamzeh(2009)conducted a series of experiments to study the buckling behavior of composite stiffened cylin-drical shells under axial load.Teter(2011)developed the finite element method and experimental method to examine the dynamic buckling behavior of a stiffened plate structure.

In addition,based on the experimental method and numerical simulation,the mechanical properties of the cylindrical shells with defects have been studied.Rahimi and Rasouli(2011)used a finite element method to study the effect of hole defects on the buckling of composite isogrid stiffened shells under axial load.Cheng,Altenhof and Li(2006)experimentally investigated the crush characteristics and energy absorption capacity of AA6061-T6 aluminum alloy extrusions with centrally located through-hole discontinuities.Chen and Ozaki(2009)proposed an approximate method for the tensile and bending stress concentrations of the hexagonal honeycomb with a single defect and examined the interaction between the two defects.

The discrete model and equivalent model are usually adopted for the design and mechanical analysis of grid structures.Although the discrete method has been widely used for modeling the mechanical behavior of the large grid structure,the ribs are commonly modeled by using beam elements,thus the complexity of the structure requires large computation consumption.As an alternative approach,the equivalent continuum model is a relatively simple and efficient analytical method.Many studies have been performed to develop the equivalent model of the grid structures.In this case,the grid structure is equivalent to a continuous solid structure with a homogenized stiffness.Many studies have been performed to assess the buckling strength of lattice shells by using equivalent models[Buragohain and Velmurugan(2009);Velmurugan and Buragohain(2007)].Based on the assessment of static equilibrium and deformation relations of the representative unit cell,the elastic constitutive relations and failure criterion of planar lattice composites were established[Zhang,Fan and Fang(2008)].Totaro and Gurdal(2009)conducted the optimal design of lattice shells subjected to axial compressive loads by using the continuum model.Cui,Zhang,Zhao,Lu and Fang(2010)developed an equivalent model to analytically calculate the specific stress fields of the triangular and Kagome lattices with a single-bar defect by using the principle of superposition and a stripe method.Taking into account the geometric and mechanical properties of the coated corrugated panel,an analytical homogenization model was proposed by Dayyani,Friswell,Ziaei-Rad and Flores(2013).An equivalent monocoque shell theory was developed by Sun,Fan,Zhou and Fang(2013)to predict the mechanical behavior of the quasi-isotropic sandwich cylinder,including the deformation and the multi-mode failure criterion.

In this paper,an equivalent method is presented to study the impact response of isogrid cylinders and isogrid-stiffened cylinders.The isogrid cylinder is modeled as an equivalent continuous cylinder with the effective density,modulus and thickness.To investigate the effective properties,different aspects of the isogrid structure that include impact speed,relative density and relative thickness are examined in this paper.Through the analysis of the equivalent performance of the grid structure,a stiffened cylindrical structure can be treated as a continuum shell.The effects of shell thickness and the cross section shape of the ribs on the equivalent performance are discussed.Then,the equivalent model is used to analyze the load-bearing capacity of the isogrid-stiffened cylindrical shells with and without an elliptical hole.Based on the equivalent model,the load-bearing capacity of cylindrical shell structures is numerically studied by using the finite element method.The numerical results show that a reasonable equivalence of the grid structure can reduce the computational cost and provide a convenient approach to study the mechanical properties and impact behavior of more complicated grid-stiffened structures.

2 Equivalent model of isogrid structure

The equilateral triangle grid(isogrid)structure can be treated as a transversely isotropic elastic body.Based on the equivalence model,the effective material parameters such as effective density,elastic modulus and Poisson’s ratio can be determined.These material parameters were used to build the equivalent continuum cylinder model.For an equilateral triangle grid(isogrid)structure,the transversely isotropic constitutive relation can be written as:

As shown in Fig.1,because two unit cells share one rib,the mass of the triangle frame can be expressed as 3ρsT bL/2.After equivalence,the mass of the triangle plate can be expressed as ρ∗bLLsin60o/2.After equivalence the mass remains unchanged.The relative density of the isogrid structure can be given by

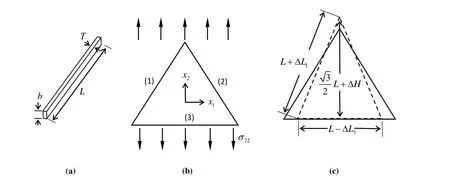
Figure 1:Schematic of a triangle unit cell,(a)rib diagram,(b)force diagram,(c)deformation diagram.

The effective strain of the unit cell is defined by

where ΔL1and ΔL3are the deformation of bar 1 and bar 3 and ΔH is the dimensional change in the x2direction.The extension of each bar is readily given as

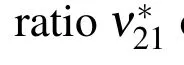
The triangle unit cell is assumed to be transversely isotropic material,and the inplane elastic parameters have the relations E∗1=E∗2and ν∗12=ν∗21.The in-plane shear modulus can be obtained as

To determine the elastic stiffness matrix,E∗3,ν∗13,and G∗13need to be solved.It is as-sumed that along the x3(out-of-plane)direction,the stress is uniformly distributed within the cell wall.Thus,

In the x3direction,because the internal stress of the cell wall is uniform and equal,the effective Poisson’s ratio ν1∗3is identical to that of the solid material of the unit cell,i.e.,

According to the reciprocal relations,we have

Based on the principle of minimum potential energy,the upper and lower bounds of the shear modulus in the out-of-plane region are identical,and the shear modulus can be obtained as:

3 Model validation:impact response of isogrid structure

To verify the validity of the equivalent continuum model,the impact response of an isogrid cylinder subjected to lateral impact load is considered in this section.The finite element model of an isogrid cylinder and its equivalent continuous model are shown in Fig.2.The cylinder has a height L1=272 mm,radius R=100 mm and radial thickness T1.The equilateral triangles unit cell has a side length L2=15.7 mm,height H=13.6 mm and cell wall thickness T2.The number of triangles that are circumferential and axial is 40 and 20,respectively.The cylinder was fully fixed at the upper and lower ends and was subjected to a local side impact by a rigid sphere.The radius of the sphere is 30 mm.The sphere’s initial position in the radium direction away from the cylinder center is X1=200 mm and Y1=L1/2.

In the finite element simulation,the bar of the triangle unit cell of the grid cylinder was modeled by a beam element.Each bar of the triangle unit cell was divided into 10 beam elements.The whole isogrid cylinder has 24,400 elements.The equivalent continuous solid cylinder was modeled by a shell element.The rigid sphere was modeled by a solid element.The material density of the grid is 2700 kg/m3.The elastic modulus and Poisson’s ratio of the grid are 69 GPa and 0.3,respectively.

Figure 2:Isogrid cylinder and its equivalent continuous model.

The comparison of internal energy and hourglass energy between the grid cylinder and the equivalent continuous cylinder is shown in Fig.3,where C denotes the continuous cylinder and G denotes the grid cylinder.It is shown that the result of the equivalent continuous model agrees well with that of the original grid cylinder.In entire process of impact,the total energy maintains conservation,and the proportion of hourglass energy is smaller than the required 5%of the total energy.The deformation and energy absorption are the main factors to evaluate the impact resistance capacity of a structure.For different impact velocities,the displacements of the grid structures and the equivalent continuous cylinders are shown in Fig.4.The deformation of the continuous cylinder is slightly larger than that of the isogrid cylinder for different impact velocities.

A comparison of the energy absorption for the two structures is shown in Fig.5,where I is internal energy,K is kinetic energy,and T is total energy.I/T denotes the ratio of internal energy and total energy,K/T denotes the ratio of kinetic energy and total energy.The energy absorption ratios are consistent with each other for two types of structures.In the two structures,I/T increases and K/T decreases as the impact progresses.At last,all of the impact energy is absorbed.However,the energy absorption of the equivalent continuous cylinder is greater than that of the grid cylinder.For a strain of less than 50%,the internal energy conversion rate of the equivalent structure is smaller than that of the grid structure.For a strain that is larger than 50%,the internal energy conversion rate of the grid structure is significantly lower.In this case,the internal energy conversion rate of the equivalent structure remains unchanged.

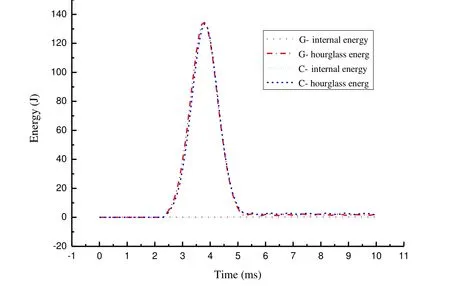
Figure 3:Variations of nternal energy and hourglass energy versus time.

4 Impact behavior of grid-stiffened cylindrical shells

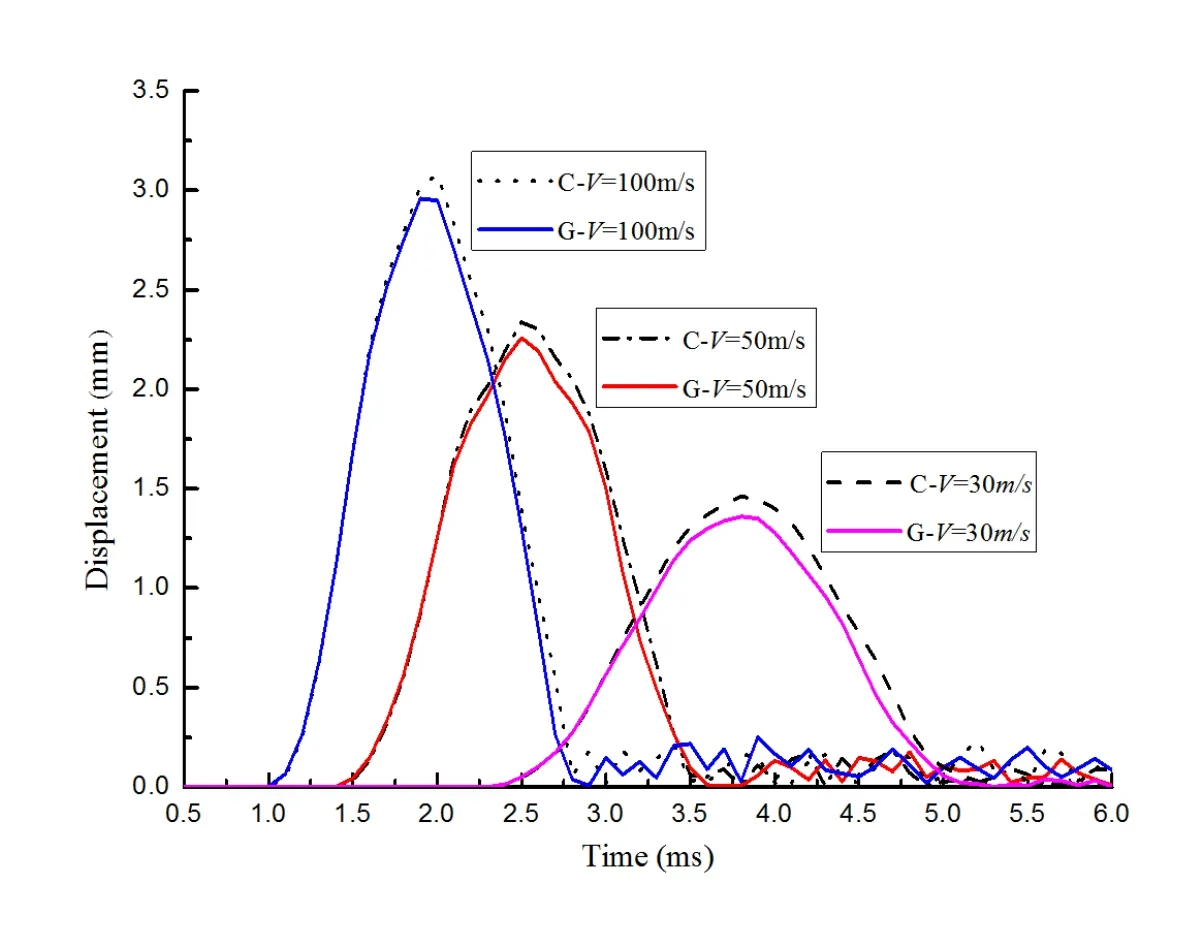
Figure 4:Displacement of isogrid and continuous structures under different velocities.

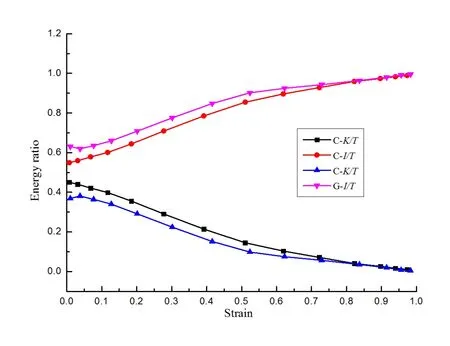
Figure 5:Energy absorption of isogrid and continuous structures(V=30 m/s).

Stiffened cylindrical shells consist of the skin and ribs.The equivalent continuous structure of the isogrid structure is used to study the impact performance of the stiffened cylindrical shell.The ribs are transformed to a solid continuous shell.Thus,the stiffened cylindrical shell is transformed to a laminated solid shell,as shown in Fig.6.The cylinder has a height L1=200 mm and diameter R=58 mm.The skin and ribs are an elastoplastic material with a density of 2700 kg/m3,an elastic modulus of 69 GPa,a Poisson’s ratio of 0.3 and a yield stress of 76 MPa.For the comparison,the stiffened shell and equivalent shell are analyzed,respectively.The element Shell163 for the smooth shell and element Beam161 for the ribs are used.

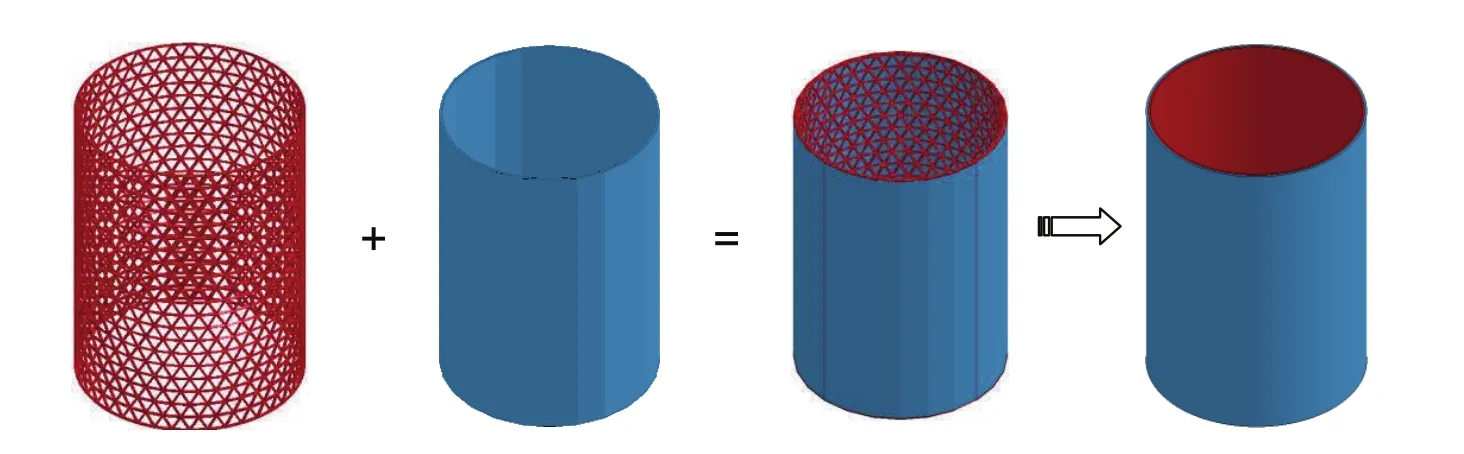
Figure 6:Equivalency of stiffened cylindrical shell.

The impact deformation is shown in Fig.7.As seen here,the deformation trends of the equivalent model and real shell structure are basically the same.However,the deformation of the equivalent model is greater than that of the real stiffened shell structure.

The relations between the deformation and thickness ratio H1/H2is shown in Fig.8,where H1is the thickness of the skin and H2is the thickness of the ribs.It can be seen that for the large thickness of the skin,the deformation of the equivalent model is closer to that of the real structure.For the large thickness ratio,the relatively small differences can be induced by the equivalency.In fact,the large thickness ratio of the shell means the skins dominates the mechanical behavior of the stiffened shell.It is noted that the deformation of the shell with a large thickness ratio will trend to a constant value,i.e.,the deformation of a smooth shell.

The energy absorption capability of the structure is shown in Fig.9.Because of the equivalency of the rib,a slight difference in the energy absorption capability between the equivalent and real structures can be found.The energy absorption capacity of the rib option in an equivalent model is less than that in a real shell structure.It is shown that the deformation of the equivalent model is greater than the deformation of the real shell structure.This implies that the equivalency leads to a decrease in the energy absorption ability of the ribs and an increase in the energy absorption ability of the skin option.

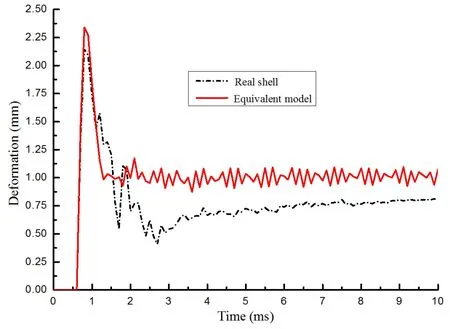
Figure 7:Deformation of the real and equivalent structures.

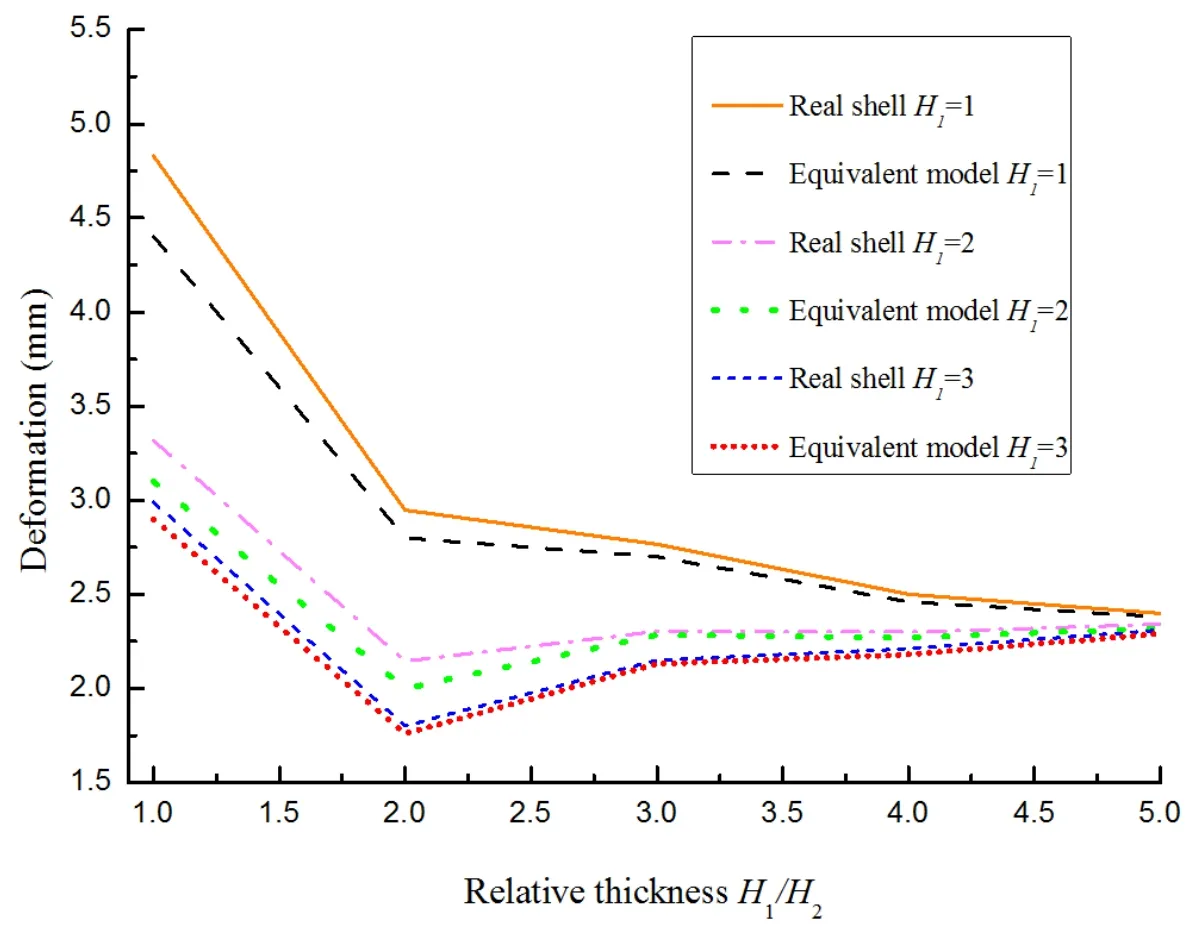
Figure 8:Relations between deformation and relative thickness.

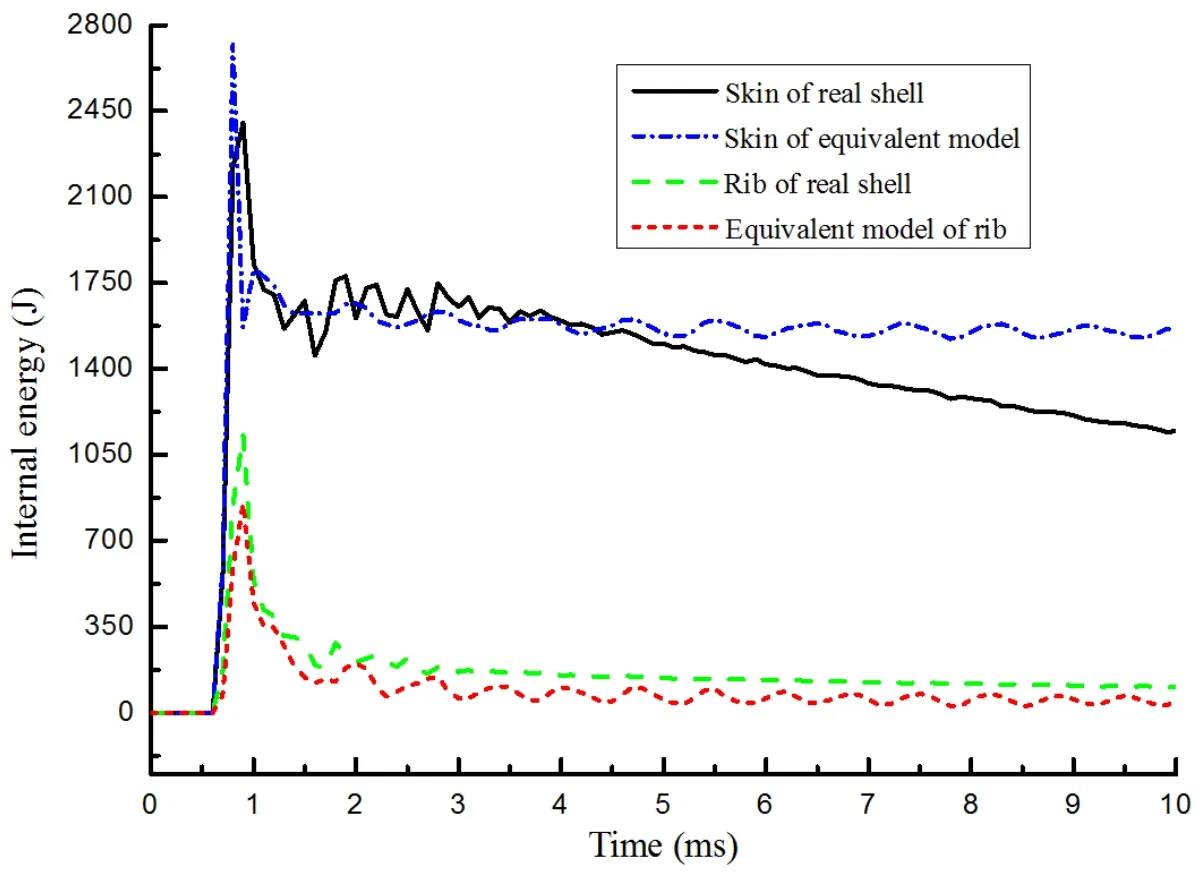
Figure 9:Energy absorption capability of stiffened shell.

5 Impact resistance of grid-stiffened cylindrical shell with a hole

The grid-stiffened cylindrical shell with holes has been widely used in many practical engineering fields.When the structure is subjected to external loads,the existence of the hole results in serious stress concentration,which leads to a reduction in the load-carrying capacity of the structure.As a result,the impact resistance and stability of the cylindrical shell are also greatly affected.To simplify the study,the equivalent model is used to investigate the mechanical behavior of the cylindrical shell with an elliptical hole.The dimensions of the cylindrical shell are the same as the previous example.As shown in Fig.10,the distance of the elliptical hole from the bottom of the shell is L0,and the length of the major axis and minor axis is a and b,respectively.

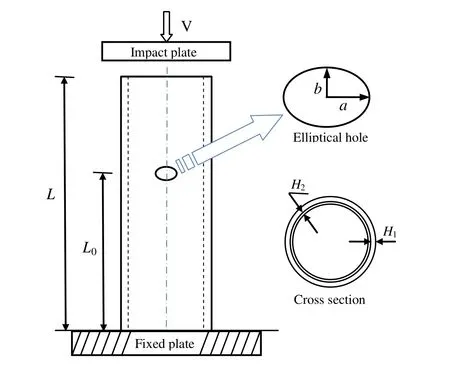
Figure 10:Schematic of stiffened cylindrical shell with an elliptical hole.

The relations between the load-bearing capacity and shape of the elliptical hole are shown in Fig.12.With an increase in the ratio of major axis to minor axis,the maximum load-bearing capacity and the mean load-bearing capacity of the cylindrical shell are approximately linear.Under the axial impact load,axial buckling of the cylindrical shell is the main factor that influences the load-bearing capacity.For the smaller ratio of major to minor axes,the buckling of the stiffened cylindrical shell is impeded by an elongated hole along the direction of impact.Therefore,the impact resistance and load-bearing capacity of the structure is enhanced.For ana/bof 0.285 and different locations of an elliptical hole,the curves of mean impact force and deformation are shown in Fig.13.In the initial stage,the peak of the curves is slightly different.With an increase inL0,the mean forces are closer to the result of the cylinder without the hole.This means that there is a limited influence of the hole because the hole is located near the impacted end.

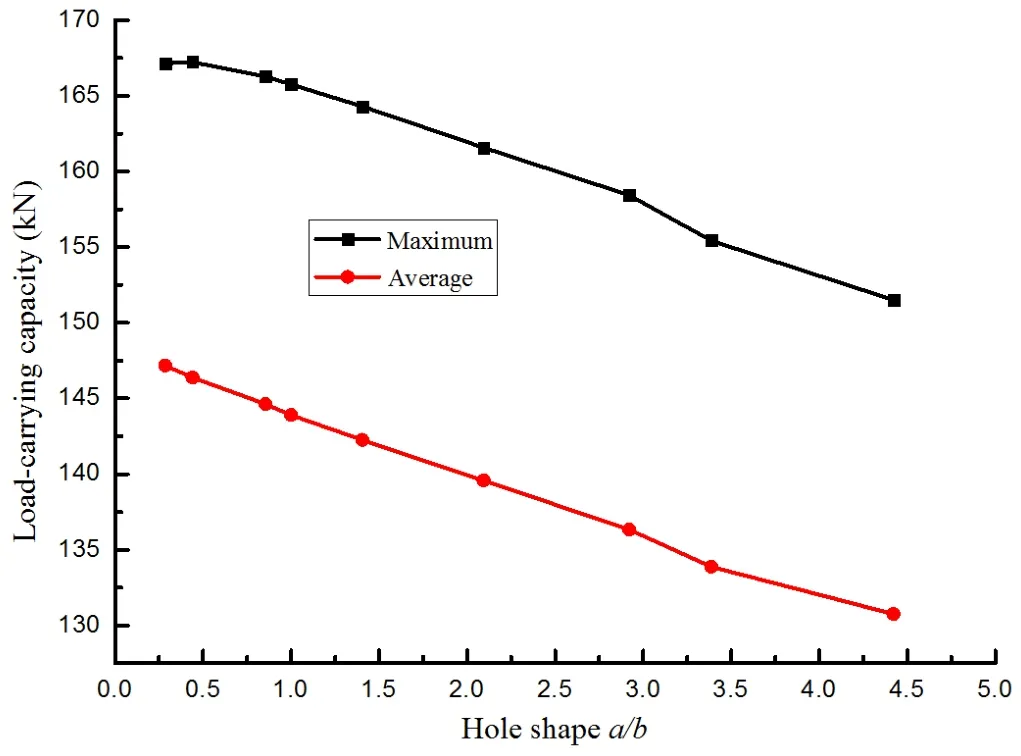
Figure 12:Relations between load-bearing capacity and hole shape.

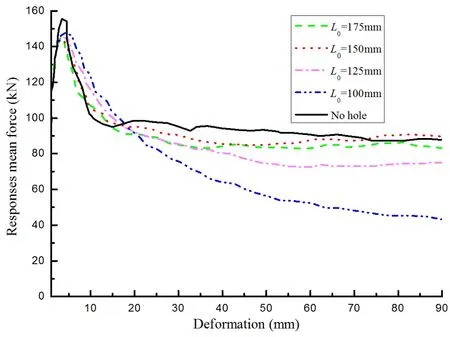
Figure 13:Relations between mean impact force and deformation for different locations of the hole.

6 Conclusions

In this paper,the isogrid structure is modeled as a continuous solid with a homogenized stiffness.The equivalent continuum model provides a relatively simple and efficient analytical method.The accuracy of the equivalent model was verified by using numerical examples.The impact response of the grid structure has been reflected well.Then,the equivalent model was utilized to analyze the impact response of the isogrid-stiffened cylindrical shell.

The impact resistance of the isogrid structures is influenced by the impact velocity and relative density of the isogrid.It is found that for the same impact load,the deformation of the grid structure is smaller than that of the equivalent continuous structure,while the energy absorption ability of the grid structure is stronger than that of the equivalent continuous structure.The relative density is a key factor that affects the equivalent performance of the grid structures.

The grid-stiffened cylindrical shell is equivalent to the smooth laminated shell.Because of the equivalence,the energy absorption ability of the ribs is slightly underestimated,and the energy absorption ability of the skin is overestimated.Overall,the equivalent model can provide a satisfied result for the impact resistance and energy absorption of the grid-stiffened shell.The location and shape of the hole on the shell can considerably influence the load-bearing capacity of the cylinder

Acknowledgement:The financial support from the Natural Science Foundation of China under grants#11172012,#11472020 and the National Key Technology R&D Program under grant#2012BAK29B00 is gratefully acknowledged.

Adachi,T.;Tomiyama,A.;Araki,W.;Yamaji,A.(2008):Energy absorption of a thin-walled cylinder with ribs subjected to axial impact.Int.J.Impact.Eng.,vol.35,pp.65-79.

Bakhvalov,Y.O.;Petrokovsky,S.A.;Polynovsky,V.P.;Rasin,A.F.(2009):Composite irregular lattice shells designing for space applications.In:17th International Conference on Composite Materials,Edinburgh,SCO.

Buragohain,M.;Velmurugan,R.(2009):Buckling analysis of composite hexagonal lattice cylindrical shells using smeared stiffener model.Defence Sci.J.,vol.59,pp.230-238.

Cheng,Q.W.;Altenhof,W.;Li,L.(2006):Experimental investigations on the crush behaviour of AA6061-T6 aluminum square tubes with different types of through-hole discontinuities.Thin Wall Struct.,vol.44,pp.441-454.

Chen,D.H.;Ozaki,S.(2009):Stress concentration due to defects in a honeycomb structure.Compos.Struct.,vol.89,pp.52-59.

Cui,X.D.;Zhang,Y.H.;Zhao,H.;Lu,T.J.;Fang,D.N.(2010):Stress concentration in two dimensional lattices with imperfections.Acta.Mech.,vol.216,pp.105-122.

Dayyani,I.;Friswell,M.I.;Ziaei-Rad,S.;Flores,E.I.S.(2013):Equivalent models of composite corrugated cores with elastomeric coatings for morphing structures.Compos.Struct.,vol.104,pp.281-292.

Djeukou,A.;von Estorff,O.(2009):Low-velocity impact of composites plates using the Radial Point Interpolation Method.CMES-Computer Modeling In Engineering&Sciences,vol.47,pp.23-42.

Fan,H.L.;Jin,F.N.;Fang,D.N.(2009):Uniaxial local buckling strength of periodic lattice composites.Mater.Des.,vol.30,pp.4136-4145.

Ghavami,K.;Khedmati,M.R.(2006):Numerical and experimental investigations on the compression behaviour of stiffened plates.J.Constr.Steel Res.,vol.62,pp.1087-1100.

Han,X.;Liu,G.R.;Li,G.Y.(2004):Transient response in cross-ply laminated cylinders and its application to reconstruction of elastic constants.CMCComputers Materials&Continua.vol.1,pp.39-49.

Jing,L.;Xi,C.Q.;Wang,Z.H.;Zhao,L.M.(2013):Energy absorption and failure mechanism of metallic cylindrical sandwich shells under impact loading.Mater Design,vol.52,pp.470-480.

Morozov,E.V.;Lopatin,A.V.;Nesterov,V.A.(2011):Finite-element modelling and buckling analysis of anisogrid composite lattice cylindrical shells.Compos.Struct.,vol.93,pp.308-323.

Oshiro,R.E.;Alves,M.(2007):Scaling of cylindrical shells under axial impact.Int.J.Impact.Eng.,vol.34,pp.89-103.

Poorveis,D.(2006):Buckling ofdiscretely stringer-stiffened composite cylindrical shells under combined axial compression and external pressure.Sci.Iran,vol.13,pp.113-123.

Rahimi,G.H.;Zandi,M.;Rasouli,S.F.(2013):Analysis of the effect of stiffener profile on buckling strength in composite isogrid stiffened shell under axial loading.Aerosp Sci Technol,vol.24,pp.198-203.

Rahimi,G.H.;Rasouli,F.(2011):Study on square and rectangular cutouts and their aspect ratios on buckling of composite isogrid stiffened shell under axial loading.In:10th Conference of Iranian Aerospace Society,Tehran,IR.

Rajendran,A.M.;Grove,D.J.(2002):Computational modeling of shock and impact response of alumina.CMES-Computer Modeling In Engineering&Sciences,vol.3,pp.367-380.

Souli,M.;Gabrys,J.(2012):Fluid Structure Interaction for Bird Impact Problem:Experimental and Numerical Investigation.CMES-Computer Modeling In Engineering&Sciences,vol.85,pp.177-192.

Sun,F.F.;Fan,H.L.;Zhou,C.W.;Fang,D.N.(2013):Equivalent analysis and failure prediction of quasi-isotropic composite sandwich cylinder with lattice core under uniaxial compression.Compos.Struct.,vol.101,pp.180-190.

Teter,A.(2011):Dynamic critical load based on different stability criteria for coupled buckling of columns with stiffened open cross-sections.Thin Wall Struct.,vol.49,pp.589-595.

Totaro,G.(2012):Local buckling modelling of isogrid and anisogrid lattice cylindrical shells with triangular cells.Compos.Struct.,vol.94,pp.446-452.

Totaro,G.(2013):Local buckling modelling of isogrid and anisogrid lattice cylindrical shells with hexagonal cells.Compos.Struct.,vol.95,pp.403-410.

Totaro,G.;Gurdal,Z.(2009):Optimal design of composite lattice shell structures for aerospace applications.Aerosp.Sci.Technol.,vol.13,pp.157-164.

Vasiliev,V.V.;Barynin,V.A.;Rasin,A.F.(2001):Anisogrid lattice structures–survey of development and application.Compos.Struct.,vol.54,pp.361-370.

Vasiliev,V.V.;Barynin,V.A.;Razin,A.F.(2012):Anisogrid composite lattice structures–Development and aerospace applications.Compos.Struct.,vol.94,pp.1117-1127.

Vasiliev,V.V.;Razin,A.F.(2006):Anisogrid composite lattice structures for spacecraft and aircraft applications.Compos.Struct.,vol.76,pp.182-189.

Velmurugan,R.;Buragohain,M.(2007):Buckling analysis of grid-stiffened composite cylindrical shell.J Aero Sci Technol,vol.59,pp.282-293.

Yazdani,M.;Rahimi,H.;Khatibi,A.A.;Hamzeh,S.(2009):An experimental investigation into the buckling of GFRP stiffened shells under axial loading.Sci.Res.Essays.,vol.4,pp.914-920.

Yazdani,M.;Rahimi,H.(2010):The effects of helical ribs’number and grid types on the buckling of thin-walled GFRP-stiffened shells under axial loading.J.Reinf.Plast.Compos.,vol.29,pp.2568-2575.

Zhang,Y.H.;Xue,Z.Y.;Chen,L.M.;Fang,D.N.(2009):Deformation and failure mechanisms of lattice cylindrical shells under axial loading.Int.J.Mech.Sci.,vol.51,pp.213-221.

Zhang,Y.H.;Fan,H.L.;Fang,D.N.(2008):Constitutive relations and failure criterion of planar lattice composites.Compos.Sci.Technol.,vol.68,pp.3299-3304.

1Department of Engineering Mechanics,Beijing University of Technology,Beijing 100124,China.

2Corresponding author.Tel&Fax:86-10-67396333;E-mail:qsyang@bjut.edu.cn

3College of Civil Engineering and Architecture,Hebei University,Baoding 071002,China.

4Equipment Department,Army Aviation Institute of PLA,Beijing 101123,China.