On Improving the Celebrated Paris’Power Law for Fatigue,by Using Moving Least Squares

Leiting Dong,Robert Haynes and Satya N.Atluri

On Improving the Celebrated Paris’Power Law for Fatigue,by Using Moving Least Squares

Leiting Dong1,2,Robert Haynes3and Satya N.Atluri2

In this study,we propose to approximate the a−n relation as well as the d a/d n−ΔK relation,in fatigue crack propagation,by using the Moving Least Squares(MLS)method.This simple approach can avoid the internal inconsistencies caused by the celebrated Paris’power law approximation of the d a/d n−ΔK relation,as well as the error caused by a simple numerical differentiation of the noisy data for a−n measurements in standard fatigue tests.Efficient,accurate and automatic simulations of fatigue crack propagation can,in general,be realized by using the currently developed MLS law as the “fatigue engine”[d a/d n versus ΔK],and using a high-performance “fracture engine”[computing the K-factors]such as the Finite Element Alternating Method.

In the present paper,the “fatigue engine”based on the present MLS law,and the“fracture engine”based on the SafeFlaw computer program developed earlier by the authors,in conjunction with the COTS software ANSYS,were used for predicting the total life of arbitrarily cracked structures.

By comparing the numerical simulations with experimental tests,it is demonstrated that the current approach can give excellent predictions of the total fatigue life of a cracked structure,while the celebrated Paris’Power Law may miscalculate the total fatigue life by a very large amount.

crack growth rate,Paris’Power Law,Moving Least Squares.

1 Introduction

Modeling the fatigue behavior of cracked built-up structures is among the most important tasks for the structural integrity assessment of aircraft[Atluri(1998)].In the past several decades,the development of high-performance computer modeling techniques has enabled the highly accurate computations of fracture mechanicsparameters of cracks,and efficient automatic simulations of non-collinear and non-planar mixed-mode crack growth in complex 2D&3D structures.Among the best“fracture engines”which compute K-factors are the alternating methods developed by Atluriand co-workers,see[Nishioka and Atluri(1983);Wang and Atluri(1996);Park and Atluri(1998);Nikishkov,Park and Atluri(2001);Han and Atluri(2002);Dong and Aluri(2013a,2013b)].Such alternating methods have been embedded by the authors in software named SafeFlaw 2D&SafeFlaw 3D,which also simulate quite efficiently the non-planar mixed-mode crack propagation.

On the other hand,the development of fatigue crack growth laws,which relate the crack growth rate to fracture mechanics parameters(such as Stress Intensity Factors),is more likely to be an empirical art than a strict science.Having observed the linear dependence of log(d a/d n)with respect to ΔK in a certain range of crack propagation,Paris et al.(1961)were the first to propose a power law relation between the crack growth rate and the range of SIF:

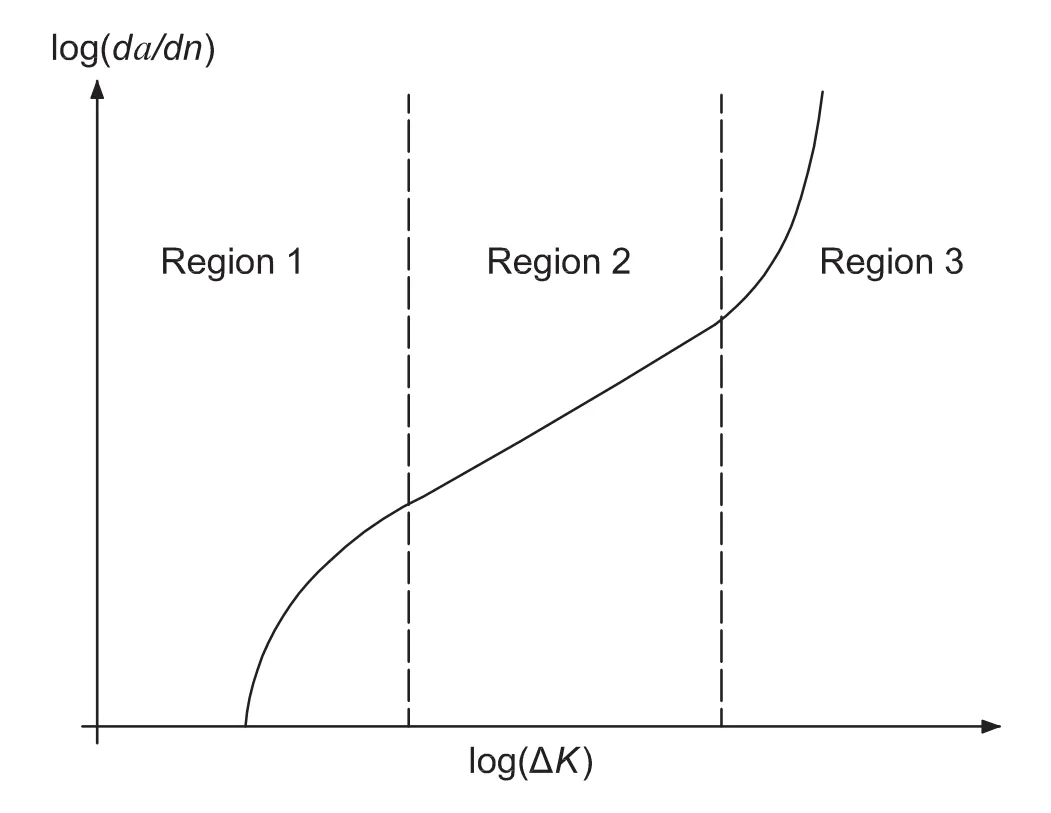
Figure 1:Typical fatigue crack growth behavior for metals.

As shown in Fig.1,although the celebrated Paris’Law can give an acceptable approximation of the crack-growth-rates in the intermediate-SIF-range(region 2),it mostly overestimates d a/d n in region 1 and underestimates d a/d n in region 3.Forman et al.(1967)proposed to modify Paris’Law by further considering the rapid crack growth near the fracture toughness KIc:

where R is the stress ratio.

And Donahue et al.(1972)proposed to replace ΔK with ΔK −ΔKthin Paris Law,in order to give a better prediction of d a/d n near the threshold SIF(ΔKth):

While both the Forman and Donahue’s formulations in Eqs.(2)-(3)apply thresholds to characterize the asymptotic behavior of d a/d n−ΔK,other studies also take into account the underlying mechanisms of plasticity,crack-closure,and even mi-crostructure,see the review by[Newman(1998)].For example,Elber(1970)proposed to use ΔKeffinstead of ΔK to account for the effect of the crack closure.And crack growth rates can also be related to elastic-plastic fracture parameters such as J and T∗integrals instead of linear elastic SIFs,see[Rice(1968);Atluri(1982);Nishioka and Atluri(1982);Dowling and Begley(1976);El Haddad,Dowling,Topper and Smith(1980)].

However,considering the computational capabilities of even a present-day laptop computer,and the vast number of numerical methods available today,it is probably unnecessary to confine the development of fatigue laws to within the limited scope of power laws or very simple formulas,no matter what fracture mechanics parameters are used(ΔK,ΔKeff,ΔJ,ΔT∗,etc.).Moreover,with given discrete measurements and the attendant noisy data for the crack length(a)versus the number of cycles(n),computing d a/d n using a secant method or a piecewise polynomial method may also cause discretization errors,see ASTM E647-13a.

In this study,we propose to approximate the a−n relation as well as the d a/d n−ΔK relation using Moving Least Squares(MLS)[Atluri(2004)]instead of power laws.This simple approach can avoid the internal inconsistencies caused by the power law approximation of d a/d n−ΔK relation as well as the errors caused by simple numerical differentiation of the noisy discrete a−n data.By applying this method for fatigue life prediction of cracked structures,it is found that the current MLS law can give highly accurate estimates of the total fatigue life,while the Paris’Law may miscalculate the total fatigue life by several multiples or even an order of magnitude.Although the current study only considers ΔK as the driving parameter with the assumption of perfect linear elasticity,other effects such as plasticity and crack closure can also be included by using ΔKeffas the driving parameter with numerical techniques developed by[Newman et al.(1992,1999)].With further development,it is expected that the currently developed MLS fatigue law can serve as a high-performance “fatigue engine”,which can be combined the high-performance “fracture engine”of the alternating methods,to greatly improve the state-of-the-art of structural integrity assessment and damage tolerance of fixed as well as rotary-wing aircraft.

2 A Simple Moving Least Squares Fatigue Law

2.1 Fundamentals of Moving Least Squares

The Moving Least Squares(MLS)is generally considered to be one of the best methods to interpolate random data with a high accuracy,because of its completeness,smoothness,and locality.Its formulation is briefly reviewed here,while more detailed discussions on the MLS can be found in[Atluri(2004,2005)].

Considering a one-dimensional space with n being the independent variable and a being the dependent variable,the MLS method starts by expressing a(n)as polynomials:

where pT(n)represents the monomial basis.In this study,we use a second-order interpolation,so that pT(n)=[1,n,n2].b(n)is a vector containing the coefficient functions of each monomial basis,which can be determined by minimizing the following weighted least squares objective function:

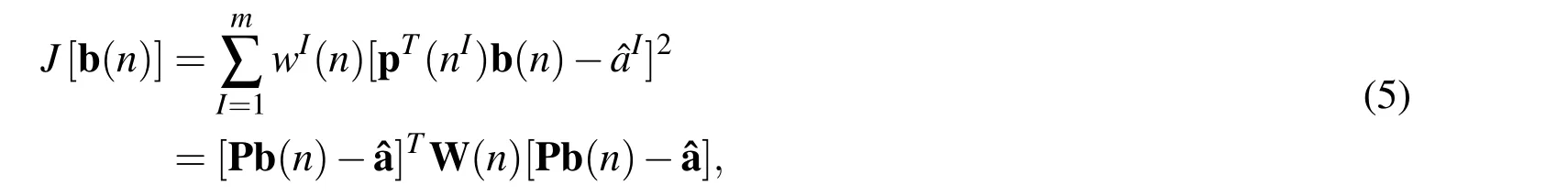
where nI,I=1,2,···,m is a group of discrete nodes withˆaIbeing the fictitious nodal value at node I.Differing from the traditional Least Squares Method,the MLS weight function wI(n)is a local function which vanishes outside the support size(rI)of node I.In this study,a fourth order spline weight function is used:

Substituting b(n)into Eq.(4),we can obtain the approximate expression of a(n)as:

where matrices A(n)and B(n)are defined by:

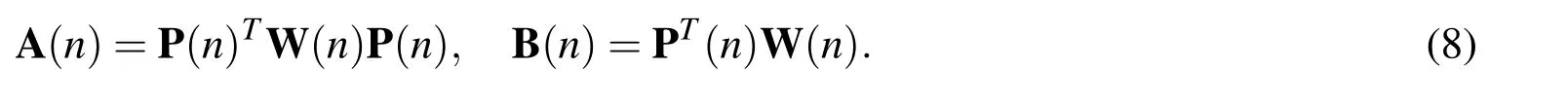
ΦI(n)is named as the MLS basis function for node I.

The derivatives of the basis functions can be computed using the following equations:

To give an example,we consider 21 uniformly distributed nodes(n=0,500,1000,...,10000),with 2000 being the support size of each node.Fig.2 plots the MLS basis function for the node at n=5000 as well as its first order derivative.As can be seen,both the basis function and its first-order derivative are smooth functions which vanish outside the support range of each node.

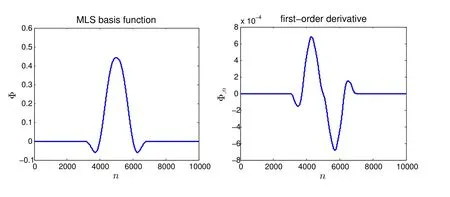
Figure 2:MLS basis function and its first order derivative.

2.2 Numerical Differentiation of Discrete a−n Data Using MLS

Fatigue tests generally give discrete pairs of a−n data which can often be noisy.Suppose one has measured crack sizes a1,a2,...,amat cycles n1,n2,...,nm,then by using n1,n2,...,nmas MLS nodes,the a−n relation can be approximated as a continuous function:

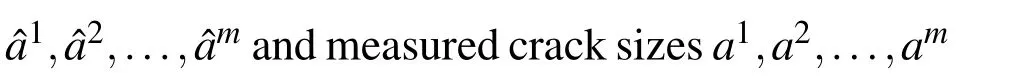
The crack growth rates can thus be computed by directly differentiating Eq.(10)with the aid of Eq.(9):

In this study,we consider 7075-T6 aluminum alloy,and use the fatigue test data given in NASA/TM-2005-213907 report.Three test specimens were prepared following the ASTM E647-00 standard,i.e.AL-7-21,AL-7-22 and AL-7-23.A schematic plot of a middle tension M(T)specimen is given in Fig.3,where W=102 mm,B=3.18 mm.Each specimen had different initial crack sizes,and was loaded with different magnitudes of forces,while having the same stress ratio(R=0.1).Any data that satisfies W−2a≥1.25Pmax/(BσYS)were rejected to rule out the effects of inelastic material response.Fig.4 gives the fitted a−n curve as well as the thereafter derived crack growth rates d a/d n.

2.3 An Empirical d a/d n−ΔK Relation by MLS Approximation

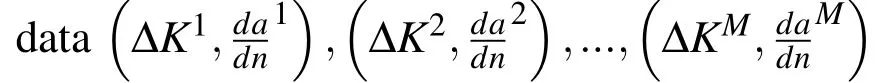
Figure 3:Schematic of a middle tension M(T)specimen by[Forth,Wright,and Johnson(2005)].

And the fictitious nodal values can be determined by minimizing the following simple quadratic objective function:

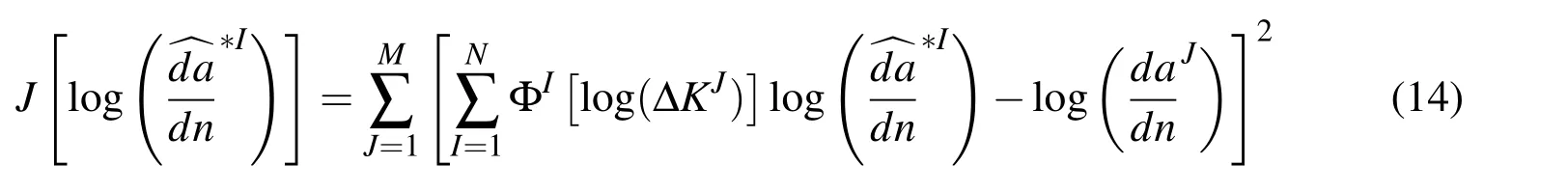
In this study,10 uniformly distributed(in the log scale)MLS nodes are used for demonstration,and the approximated d a/d n−ΔK relation is plotted in Fig.5.As can be seen,a very accurate prediction of crack-growth rates is obtained by using only a few MLS nodes,in contrast to the simple deviation of the Paris’Law.

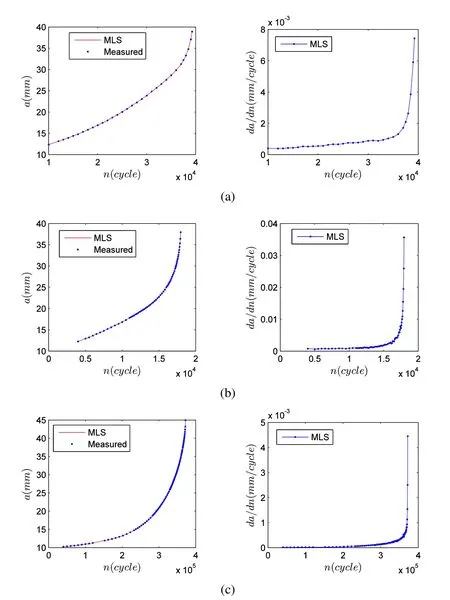
Figure 4:Using Moving Least Squares to numerically differentiate discrete a−n data given by[Forth,Wright,and Johnson(2005)]:(a)AL-7-21,(b)AL-7-22,(c)AL-7-23.

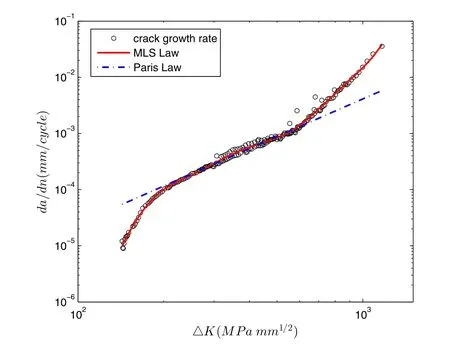
Figure 5:Approximating the d a/d n−ΔK relation using Paris’Law as well as the Moving Least Squares(MLS).

3 Fatigue Crack Growth Simulation by the Currently Developed MLS Law

In this section,we verify the capability of a highly-accurate fatigue life assessment using the currently developed MLS fatigue law.This is done by implementing the MLS law into the well-established Finite Element Alternating Method[Park and Atluri(1998)].The FEAM enables a fast and accurate computation of ΔK,as well as an automatic simulation of crack growth.With the newly developed MLS law,the fatigue life of a cracked structure can be computed by numerically evaluating:

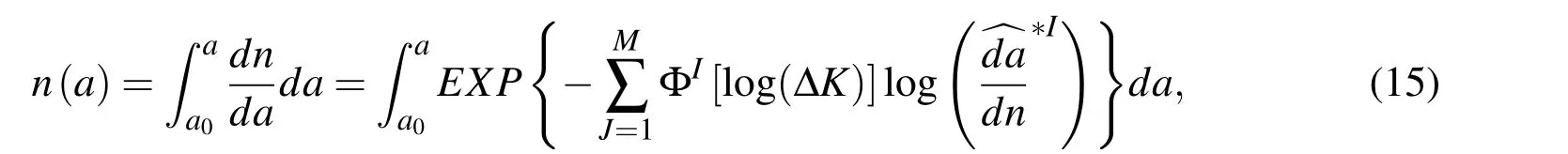
where E X P{·}is the exponential function and a0is the initial crack size.Similarly,FEAM can also be combined with Paris’Law to simulate fatigue crack growth,the results of which are used for comparison in this study.

The present approach is firstly applied to model the fatigue behavior of M(T)specimens of NASA/TM-2005-213907 report used in section 2.As shown in Fig.6-7,Paris’Law greatly underestimates the fatigue life of AL-7-23,this is because ΔK for this specimen is relatively small(near threshold region).Paris’Law also underestimates the crack growth rates of AL-7-22,where ΔK for this specimen is relatively large(near fracture toughness region).In contrast,the MLS law can almost give an exact estimation of the fatigue behavior of both of these 2 specimens.Because ΔK of AL-72-21 stays in the intermediate power law range,both Paris’Law and MLS give good predictions of fatigue crack growth,and thus the results for AL-72-21 are not plotted here.

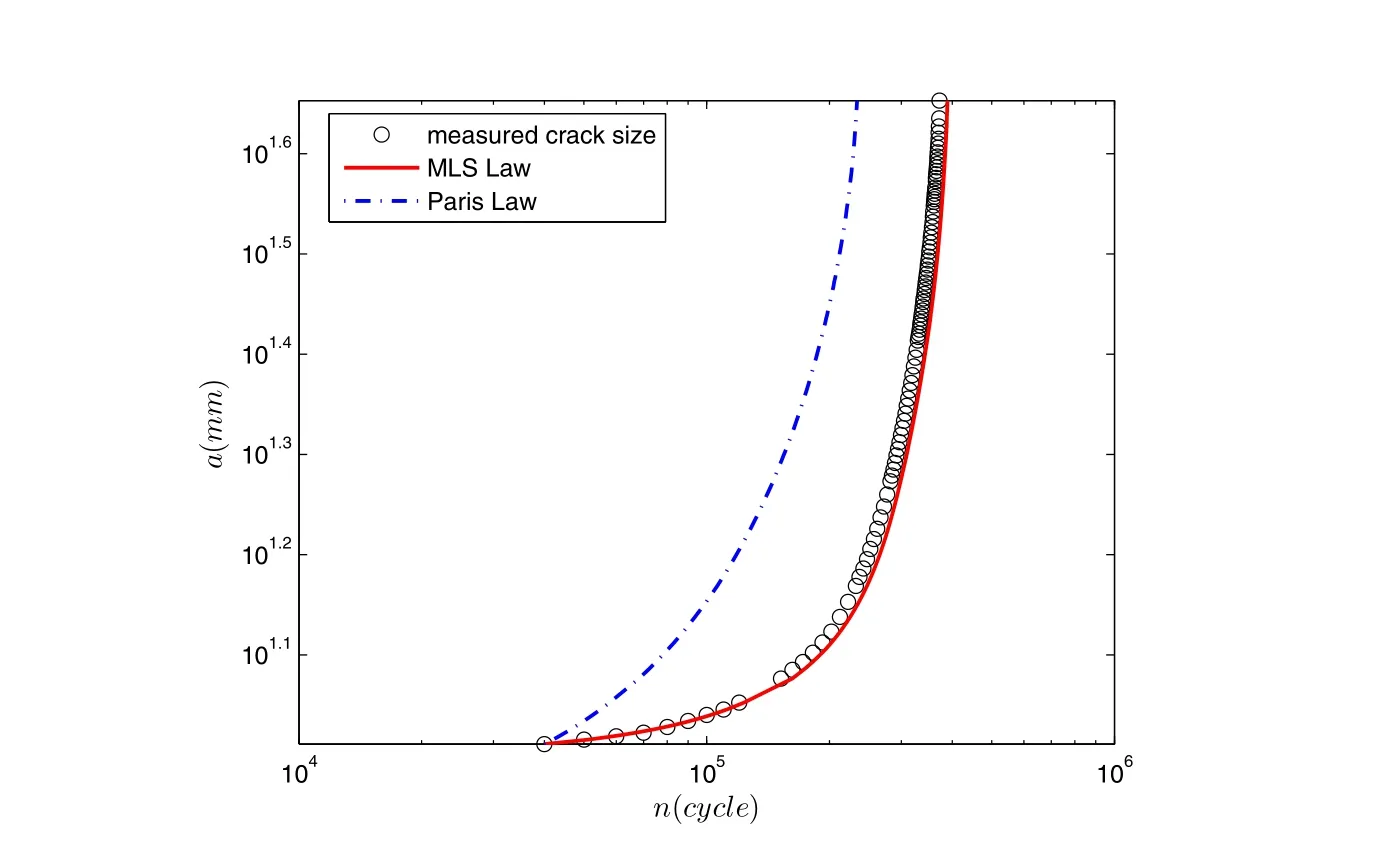
Figure 6:Predicted a−n relation using Paris’Law and MLS Law,as compared to experimental results for specimen AL-7-23 in[Forth,Wright,and Johnson(2005)].

We further consider the open-hole crack experiment by[Stuart,Hill and Newman(2011)].As shown in Fig.8,each of the 3 dog-bone coupons is made of 2.03 mm thick 7075-T6 sheet.It has 381 mm in total length and is 88.9 mm wide at the gripped ends.The gripped ends taper to a central gage section(44.5 mm wide and 88.9 mm long)with a centrally located open hole which is 7.09 mm in diameter.The initial crack is 0.381 mm in size(including the notch&the pre-crack).The applied maximum gross tress is 47.2 M Pa,with a stress ratio of 0.1.

This problem is solved by using the FEAM combined with Paris’as well as the present MLS fatigue law.As shown in Fig.9,the Paris’Law underestimates the fatigue life by a factor of 3,while the MLS law can accurately simulate the fatigue growth of the crack near the open hole.Again,this is because the Paris’Law overestimates the crack growth rates in the near threshold region,while the currently developed MLS fatigue law gives very accurate predictions of crack growth rates in the threshold,intermediate,as well as the near fracture toughness regions.

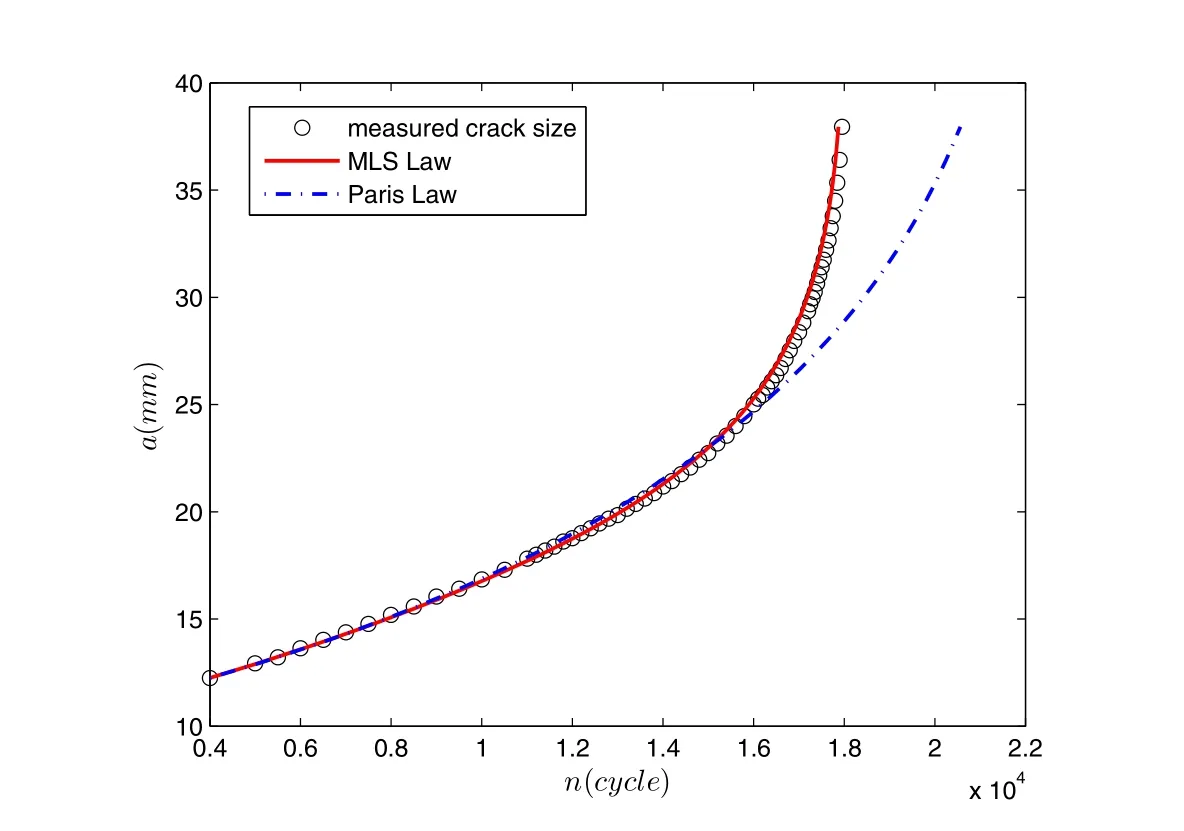
Figure 7:Predicted a−n relation using Paris’Law and MLS Law,as compared to experimental results for specimen AL-7-22 in[Forth,Wright,and Johnson(2005)].

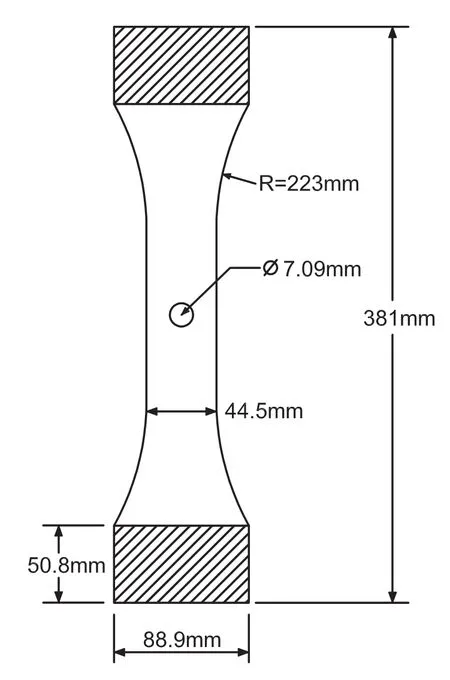
Figure 8:Open-hole Al7075-T6 couponsused in[Stuart,Hill and Newman(2011)]with one single mode-1 crack at the right side of the hole.

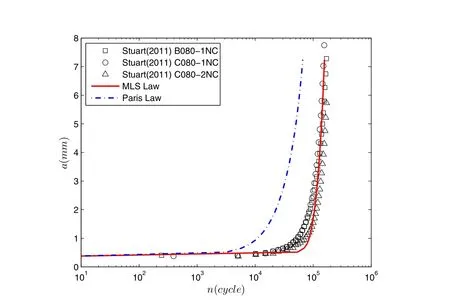
Figure 9:Predicted a−n relation using Paris’Law and MLS Law,as compared to experimental results of 3 specimens in[Stuart,Hill and Newman(2011)].

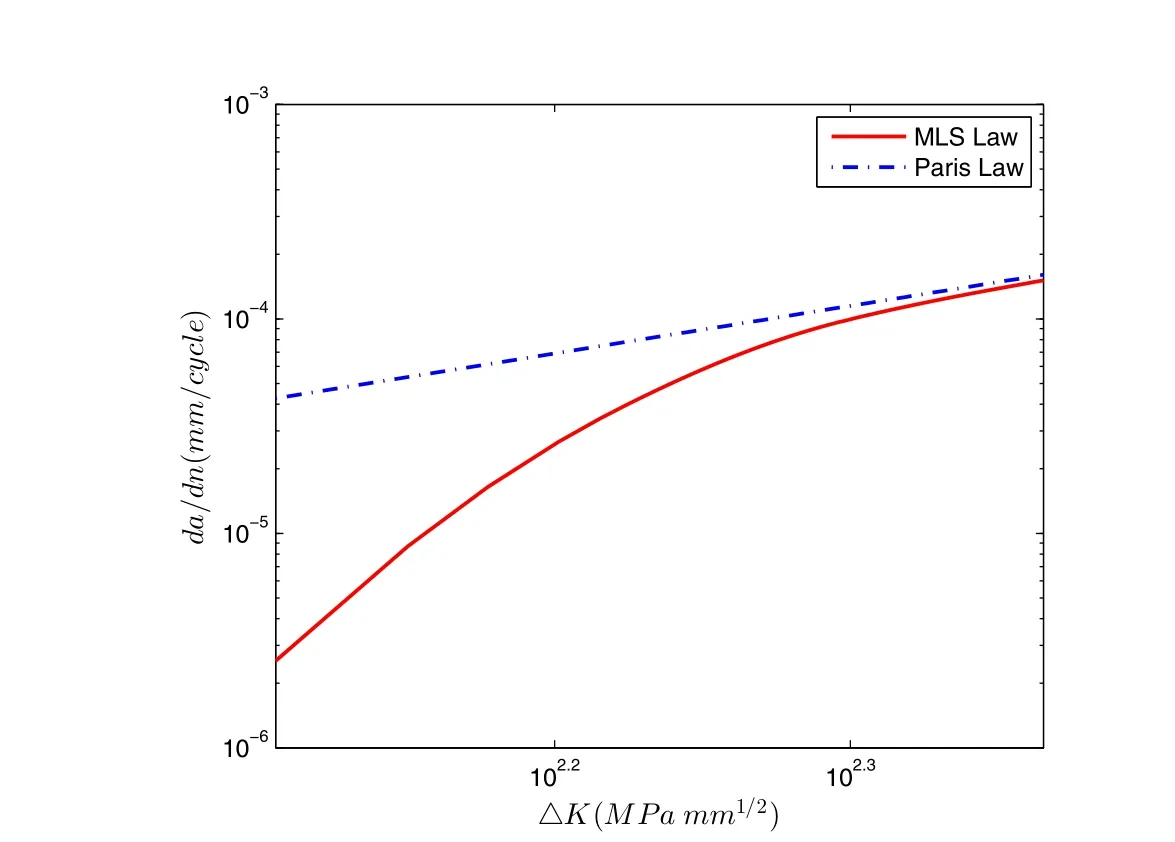
Figure 10:Predicted da/dn−ΔK relation using Paris’s Law and MLS Law for the open-hole crack problem as given in[Stuart,Hill and Newman(2011)].

4 Conclusions

Using power laws such as the celebrated Paris’Law or other simple formulas to approximate the fatigue crack growth behavior was advantageous in the 1960s-1980s,which was the time when most of these fatigue laws were developed.However,with the rapid development of computers and numerical methods in the past half of a century,much better fatigue crack growth relations can be postulated today.This paper presents a preliminary demonstration of how much better predictions of crack growth rates and the total remaining fatigue life can be achieved by using the Moving Least Squares approximations.Other high-performance meshless approximating methods using Partitions of Unity,Shephard Functions,Radial Basis Functions,etc.[Atluri(2004)]will also be explored in the very near future.Moreover,effects of plasticity and crack closure can also be taken into account by simple corrections ofK−factors,which will be considered in our future studies.

In the present paper,the “fatigue engine”based on the present MLS law,and the“fracture engine”based on the SafeFlaw computer program developed earlier by the authors,in conjunction with the COTS software ANSYS,were used for predicting the total life of arbitrarily cracked structures.

Acknowledgement:This work was supported by Vehicle Technology Division of the Army Research Labs.The support and encouragement of Dy Le and Jaret Riddick are thankfully acknowledged.The first author also thanks the support of Natural Science Foundation Project of Jiangsu Province(Grant no.BK20140838).

ASTM-E647-13a(2014):StandardTest MethodforMeasurement of FatigueCrack Growth Rates.

Atluri,S.N.(1982):Path-independent integrals in finite elasticity and inelasticity,with body forces,inertia,and arbitrary crack-face conditions.EngineeringFracture Mechanics,vol.16,issue 3,pp.341-364.

Atluri,S.N.(1998):Structural Integrity and Durability,Tech Science Press.

Atluri,S.N.(2004):The meshless method(MLPG)for domain&BIE discretiza-tions.Tech Science Press.

Atluri,S.N.(2005):Methods of Computer Modeling in Engineering&the Sciences(Vol.1),Tech Science Press.

Donahue,R.J.:Clark,H.M.:Atanmo,P.:Kumble,R.:McEvily,A.J.(1972):Crack opening displacement and the rate of fatigue crack growth.International Journal of Fracture Mechanics,vol.8,issue 2,pp.209-219.

Dong,L.;Atluri,S.N.(2013a):Fracture&Fatigue Analyses:SGBEM-FEM or XFEM?Part 1:2D Structures.CMES:Computer Modeling in Engineering&Sciences,vol.90,no.2,pp.91-146.

Dong,L.;Atluri,S.N.(2013b):Fracture&Fatigue Analyses:SGBEM-FEM or XFEM?Part 2:3D Solids.CMES:Computer Modeling in Engineering&Sciences,vol.90,no.5,pp.379-413.

Dowling,N.E.;Begley,J.A.(1976):Fatigue crack growth during gross plasticity and the J-integral.ASTM STP 590,pp.82-103.

Elber,W.(1970):Fatigue crack closure under cyclic tension.EngineeringFracture Mechanics,vol.2,issue 1,pp.37-45.

El Haddad,M.H.:Dowling,N.E.:Topper,T.H.;Smith,K.N.(1980):J integral applications for short fatigue cracks at notches.International Journal of Fracture,vol.16,issue 1,pp.15-30.

Forth,S.C.;Wright,C.W.;Johnston Jr,W.M.(2005):7075-T6 and 2024-T351 aluminum alloy fatigue crack growth rate data.NASA/TM-2005-213907.

Forman,R.G.;Kearney,V.E.;Engle,R.M.(1967):Numerical analysis of crack propagation in cyclic-loaded structures.Journal of Fluids Engineering,vol.89,issue 3,pp.459-463.

Han,Z.D.;Atluri,S.N.(2002):SGBEM(for Cracked Local Subdomain)–FEM(for uncracked global Structure)Alternating Method for Analyzing 3D Surface Cracks and Their Fatigue-Growth.CMES:Computer Modeling in Engineering&Sciences,vol.3,no.6,pp.699-716.

Newman,J.C.(1992):FASTRAN 2—a fatigue crack growth structural analysis program.NASA STI/Recon Technical Report N,92,30964.

Newman,J.C.(1998):The merging of fatigue and fracture mechanics concepts:a historical perspective.Progress in Aerospace Sciences,vol.34,issue 5,pp.347-390.

Newman,J.C.;Phillips,E.P.;Swain,M.H.(1999):Fatigue-life prediction methodology using small-crack theory.International Journal of fatigue,vol.21,issue 2,pp.109-119.

Nishioka,T.;Atluri,S.N.(1982):Analytical solution for embedded elliptical cracks and finite element alternating method for elliptical surface cracks,subjected to arbitrary loadings.Engineering Fracture Mechanics,vol.17,pp.247-268.

Nishioka,T.;Atluri,S.N.(1983):Path-independent integrals,energy release rates,and general solutions of near-tip fields in mixed-mode dynamic fracture mechanics.Engineering Fracture Mechanics,vol.18,issue 1,pp.1-22.

Nikishkov,G.P.;Park,J.H.;Atluri,S.N.(2001):SGBEM-FEM alternating method for analyzing 3D non-planar cracks and their growth in structural components.CMES:Computer Modeling in Engineering&Sciences,vol.2,no.3,pp.401-422.

Paris,P.C.;Gomez,M.P.;Anderson,W.E.(1961):A rational analytic theory of fatigue.The Trend in Engineering,vol.13.Issue 1,pp.9-14.

Park,J.H.;Atluri,S.N.(1998):Mixed mode fatigue growth of curved cracks emanating from fastener holes in aircraft lap joints.Computational Mechanics,vol.21,issue 6,pp.1333-1336.

Rice,J.R.(1968):A path independent integral and the approximate analysis of strain concentration by notches and cracks.Journal of Applied Mechanics,vol.35,issue,pp.379-386.

Stuart,D.H.;Hill,M.R.;Newman,J.C.(2011):Correlation of one-dimensional fatigue crack growth at cold-expanded holes using linear fracture mechanics and superposition.Engineering Fracture Mechanics,vol.78,issue 7,pp.1389-1406.

Wang,L.;Atluri,S.N.(1996):Recent advances in the alternating method for elastic and inelastic fracture analyses.Computer Methods in Applied Mechanics and Engineering,vol.137,issue 1,pp.1-58.

1Department of Engineering Mechanics,Hohai University,China.

2Center for Aerospace Research&Education,University of California,Irvine.

3Vehicle Technology Directorate,US Army Research Laboratory.