Dynamic Instability of Straight Bars Subjected to Impulsive Axial Loads Using the DEM

Letícia Fleck Fadel Miguel,Leandro Fleck Fadel Miguel and João Kaminski Jr.

Dynamic Instability of Straight Bars Subjected to Impulsive Axial Loads Using the DEM

Letícia Fleck Fadel Miguel1,Leandro Fleck Fadel Miguel2and João Kaminski Jr.3

Since the half of the XX century,attention was given to the instability of structures under parametric excitation,especially under periodic loads.On the other hand,the instability of bars subjected to axial loads of impulsive type has been little studied,in spite of the practical importance of the topic.Thus,in Engineering Design it is frequently supposed,without tests or additional verifications,that an axial load of short duration can exceed the Euler critical load of the bar without inducing damage in the same.Within this context,this paper proposes the use of the truss-like Discrete Element Method(DEM)for determining the dynamic response of elastic straight bars subjected to axial loads defined by pulses of short duration.The proposed approach allows the consideration of initial imperfections,as well as large displacements and other non-linear effects.The influence of the pulse duration and other effects in the response of the bar are also evaluated.Initially,the performance of the proposed methodology is verified in static and dynamic instability problems of homogeneous bars without geometrical imperfections,by comparing the DEM results with analytical solutions available in the literature.After that,the DEM is employed to analyze more complex cases,including bars with initial imperfections and non-homogeneous bars,in which material properties,as Young’s modulus and mass density,are assumed to be correlated Gaussian random fields.The proposed methodology has proven to be a useful and easy tool for analysis of dynamic instability of bars and could therefore be used by designers for estimating the dynamic buckling load.

Dynamic Instability,Critical Buckling Load,Discrete Element Me-

1 Introduction

Verification of stability of structures subjected to static loads,in particular,the determination of buckling loads,is a routine task on Structural Engineering.However,the problem of instability of structures induced by dynamic loads only started to receive attention after the Second World War,but with emphasis on the instability caused by parametric excitation;stand out in this context the contributions of Bolotin(1961).Nevertheless,few studies address the problem of instability due to transient loads,more specifically,impulsive axial loads.Koning and Taub(1933)are responsible for pioneering studies in Aeronautical Engineering on dynamic instability of bars.Davidson(1953),Huffington Jr.(1963),Ari-Guret al.(1978,1982,1997),Simitses(1990),among others,present additional studies on this topic.From these studies,it was generally accepted that,if a load is suddenly applied on a bar and then released,the bar can support a higher value than its static(slowly applied)buckling load,without inducing large damage in the bar.

Nowadays,especially due to the fact that structures have become very large and very thin,implying that any slight impact may lead to local dynamic buckling,dynamic instability has become an important factor to be taken into account during the structural design and therefore has received increasing attention.Thus,researchers have been using different approaches,such as analytical solutions,numerical simulations and experimental tests,in order to solve the problem of dynamic instability of straight bars subjected to impact axial loads.Lindberg and Florence(1987)present a detailed study on this subject.

Ari-Gur and Elishakoff(1997)presented a theoretical study of the dynamic instability of geometrically imperfect transversely isotropic columns under axial compressive pulse.The analysis included transverse shear deformation as well as translational and rotational inertia terms.The effect of transverse shear rigidity was investigated for various pulse frequencies,ranging from quasi-static to impulsive compressive loads.An appropriate dynamic instability criterion was defined and utilized and the corresponding buckling results were compared with those for isotropic columns,as well as with results obtained by the classical beam theory.The results showed that for isotropic columns the classical theory predicts accurately the dynamic buckling strength.However,for columns with low transverse shear rigidity,buckling loads predicted by the refined theory may be as low as almost two thirds of those estimated via the classical theory.These authors adopted a buckling criterion that relates the peak axial displacement at the loaded end and the peak lateral deflection to the intensity of the applied pulse force.Instability was defined as a phenomenon,when a small increase in the pulse intensity results in a relatively large increase of the displacement response.This criterion resembles the well-known Budiansky and Hutchinson(1966)and Hutchinson and Budiansky(1966)dynamic buckling criterion,for which buckling occurs when a small increase in the load intensity causes a transition from a bounded response to an unbounded one.The meaning of this criterion is that at a certain level of load intensity the axial resistance of the column is substantially reduced and a slightly stronger pulse causes its collapse.

Vincentet al.(2004),with the aim of making transmission lines more robust mechanically,decided to study the dynamic loads that the transmission line towers develop after line components fail.Broken conductor loads produce large magnitude force over a short duration(Kaminskiet al.,2008),as axial impulsive loads applied in the tower bars.The purpose of Vincentet al.(2004)were to determine if the load capacity of transmission line lattice tower structures can be increased because of short duration broken conductor loads.A series of tests was thus carried out to observe the phenomenon on a real physical line and measure,primarily,dynamic loading at various points.Fifteen tests were performed,including a final destructive test with the collapse of two towers.A broad range of measuring instruments and devices,as well as a highly customized data acquisition system,were used for the tests.Numerical simulation of the tests was also implemented by Vincentet al.(2004)using ADINA software.The results showed that failure mode is a determining factor in the amplification of longitudinal loads at towers.The dynamic response of a line subjected to an insulator string failure is not characterized by transient longitudinal imbalanced as sudden as for conductor failure.For tower failure mode,the longitudinal loads measured were smaller than the loads originating from conductor failure.In conductor failure mode,two peak loads with a very high dynamic magnification factor were observed.Should be noted that this study of Vincentet al.(2004)focused on analysis of transient response up to the elastic limit of tower members,i.e.,until a compressed member starts buckling.

Del Pradoet al.(2010)used the nonlinear finite element method to study the effect of initial geometrical imperfections on the non-linear vibrations of cable stayed masts subjected to axial time dependent loads.The non-linear equations were solved using the Newton-Raphson method associated to an arc-length technique and the Newmark method was used to calculate the time responses of the system.Validation examples were presented and the influence of initial geometrical imperfections and cable tensioning was studied when stayed towers were subjected to different types of axial loads.As Ari-Gur and Elishakoff(1997),Del Pradoet al.(2010)also used the Budianski’s criterion to study the loss of stability under sudden and harmonic loads.The results showed the great influence of both cable tensioning and cable positioning on the nonlinear behavior of the system.

Stojanovic’et al.(2011)studied free transverse vibration and buckling of a double-beam continuously joined by a Winkler elastic layer under compressive axial loading(F1and F2)with the influence of rotary inertia and shear.The motion of the system was described by a homogeneous set of two partial differential equations,which was solved by using the classical Bernoulli-Fourier method.The natural frequencies and associated amplitude ratios of an elastically connected double-beam complex system and the analytical solution of the critical buckling load were determined.The theoretical analysis was illustrated by a numerical example,in which the effect of physical parameters characterizing the vibrating system on the natural frequency,the associated amplitude ratios and the critical buckling load were discussed.These authors concluded that the critical buckling load is influenced by the ratio of the axial load F2to F1and the stiffness modulus of the Winkler elastic layer.In addition,they also found that the rotary inertia does not influence the critical buckling load model of a layered-beam system composed of two parallel Rayleigh beams,yet when the model composed of two parallel Timoshenko beams is considered,the influence of transverse shear causes a decrease in the critical buckling load.

Motamarri and Suryanarayan(2012)studied analytically the problem of dynamic elastic buckling of Euler-Bernoulli beams subjected to axial loads.A unified solution was presented as closed form analytical expressions, for peak load, time at peak load and load-deflection curve.The accuracy of the unified analytical expressions and the validity of the single mode dynamic buckling formulation were also examined by comparing with results obtained from exact solutions of the single mode formulation for various boundary conditions and with the numerical results from the dynamic response of a large number of degree of freedom finite element model.These authors concluded that the unified expressions provide a very good estimate of the buckling load over a wide range of loading rate and initial eccentricity.

Teter and Kolakowski(2013)described an analysis of dynamic response of thin walled composite columns with opened stiffened cross-sections.The columns were subjected to an in-plane pulse loading and three different stability criteria were applied:the Budiansky-Hutchinson,the Kleiber-Kotula-Saran and the phase-plane one.A pulse loading of rectangular shape was concerned.The columns were assumed to be simply supported at the ends.These authors concluded that there is a good agreement of the results obtained by the d agreement of the results obtained b.

Other researchers also studied the problem of dynamic instability in different areas of knowledge and with different approaches,such as:Fereidooniet al.(2008),Trikhaet al.(2009)and Yehet al.(2014),among others.In spite of the importance of the subject and the studies presented above,the topic is not exhausted.Simple design specifications are not yet available and constitute the subject of ongoing research efforts.Within this context,this paper proposed a new methodology to study the dynamic instability of straight bars subjected to axial impulsive loads(short pulses),using the truss-like Discrete Element Method(DEM).The proposed numerical approach is verified by comparing the obtained results with the results obtained by theoretical-analytical solutions.After confirming the good performance of the DEM in problems of static buckling of elastic straight bars,problems of dynamic instability are solved and the results are presented in graphical form,taking into account initial imperfections and large displacements.Stochastic fields for the material properties,as Young’s modulus and mass density,are also implemented in the numerical analyses,following the methodology proposed by Shinozuka and Deodatis(1996).

2 Theoretical bases

Leonhard Euler,in 1757,derived an equation that gives the maximum axial load that a long,slender,ideal column can carry without buckling.An ideal column is one that is perfectly straight,homogeneous,and free from initial stress.The Euler critical buckling load,Pcr,of a column is obtained by:

in whichEis the Young’s modulus,Iis the moment of inertia of the cross section andLfis the buckling length,whose value depends on the support conditions of the column.For one end fixed and the other end free to move laterally,Lf=2.0L;for both ends pinned(hinged,free to rotate),Lf=L;for one end fixed and the other end pinned,Lf=0.7L;for both ends fixed,Lf=0.5L;beingLthe unsupported length of the column.

The fundamental frequency of transversal vibration of a prismatic structural member(beam or column)subjected to an axial forceP0can be approximated by:

in whichf1denotes the fundamental natural frequency of the member subjected to an axial forceP0,f0denotes its reference natural frequency(i.e.,the fundamental natural frequency without the axial forceP0,obtained by Equation(3))andPcris the critical elastic buckling load of the member,obtained by Equation(1).Equation(2)gives exact results when the vibration and buckling modes are identical,constituting a satisfactory approximation when such modes are similar.

The discrete elements representation of the orthotropic continuum was adopted by the authors to solve structural dynamics problems by means of explicit direct numerical integration of the equations of motion,assuming the mass lumped at the nodes.Each node has three degrees of freedom,corresponding to the nodal displacements in the three orthogonal coordinate directions.The resulting equations of motion may be written in the well-known form:in whichrepresents the vector of generalized nodal displacements,M the diagonal mass matrix,C the damping matrix,also assumed diagonal,r(t)the vector of internal forces acting on the nodal masses and(t)the vector of external forces.Obviously,if M and C are diagonal,Equations(5)are not coupled.Then the explicit central finite differences scheme may be used to integrate Equation(5)in the time domain.Since the nodal coordinates are updated at every time step,large displacements can be accounted for in a natural and efficient manner.

Another important feature of the proposed approach is the possibility of assumption that all material properties,such as Young’s modulus(E)and mass density(ρ),are not constant throughout the structure,but random fields.That is,relevant material properties may be assumed to be correlated Gaussian random fields of the spatial coordinates.The spectral representation method proposed by Shinozuka and Deodatis(1996)for the simulation of three-dimensional homogeneous stochastic fields,which provides one value of the simulated variable at each point in a previously discretized field is employed herein.It is necessary to describe the field to be simulated by means of its power spectral density function or alternatively of its autocorrelation function.It is important to mention that there is a correlation between the same properties in adjacent elements.When the correlation length of a property,say the elasticity modulus in the x-direction,is large in relation to the size of the elements,the property will vary little between adjacent elements.The degree of correlation depends on the correlation length of the property under consideration and on the size of elements.

A new improvement in the DEM employed in this paper is the introduction of small perturbations in the cubic arrangement,generated by small initial displacements of nodal points.Basically,it is assumed that the nodes in the perturbed model are displaced from their position in a perfect cubic arrangement,defined by nodal coordinates(xn,yn,zn),as indicated below:

in whichrx,ryandrzare random numbers with a normal distribution with zero mean and coefficient of variationCVp,which is defined by the user.L0denotes the length of the longitudinal elements in the cubic cell.

Riera and Iturrioz(1998)and Rieraet al.(2011)confirmed the reliability of the method comparing DEM predictions for structures under impulsive loads with experimental results or other numerical techniques.Additionally,in other studies using DEM,Dalgueret al.(2003),Rios and Riera(2004),Miguelet al.(2006),Miguel and Riera(2007),Miguelet al.(2008),Iturriozet al.(2009),Miguelet al.(2010)and Rieraet al.(2014)contributed to demonstrate the efficiency of the method.

4 Illustrative examples

4.1 Studied member

The studied member is a steel bar,with one end fixed and the other end free to move laterally,of square cross section of 0.15×0.15m and 6.0m long,as shown in Figure 2.The bar was discretized with elements ofL0equal to 0.05m,totalizing 1080 cubic modules with 9048 DOF.Initially the material was supposed to be homogeneous,with Young’s modulusE=2.0×1011Pa,mass density ρ =7850kg/m3and Poisson’s ratio ν =0.25;and also the mesh was initially supposed does not have imperfections.

Figure 2:Studied steel bar discretized with DEM.

4.2 Static analysis

Initially supposing that the bar is homogenous and the mesh is not perturbed,the numerical simulation using DEM is carried out applying the load very slowly,simulating a static analysis.The bar is subjected to an axial compression load increasing slowly and lineally with the time.

The analytical result for the Euler critical buckling load,applying Equation(1),isPcr=5.783×105N.Figure 3 shows a graph of axial compression loadversusdisplacement in the free end in the direction perpendicular to the load application,while Figure 4 shows the corresponding Southwell plot.

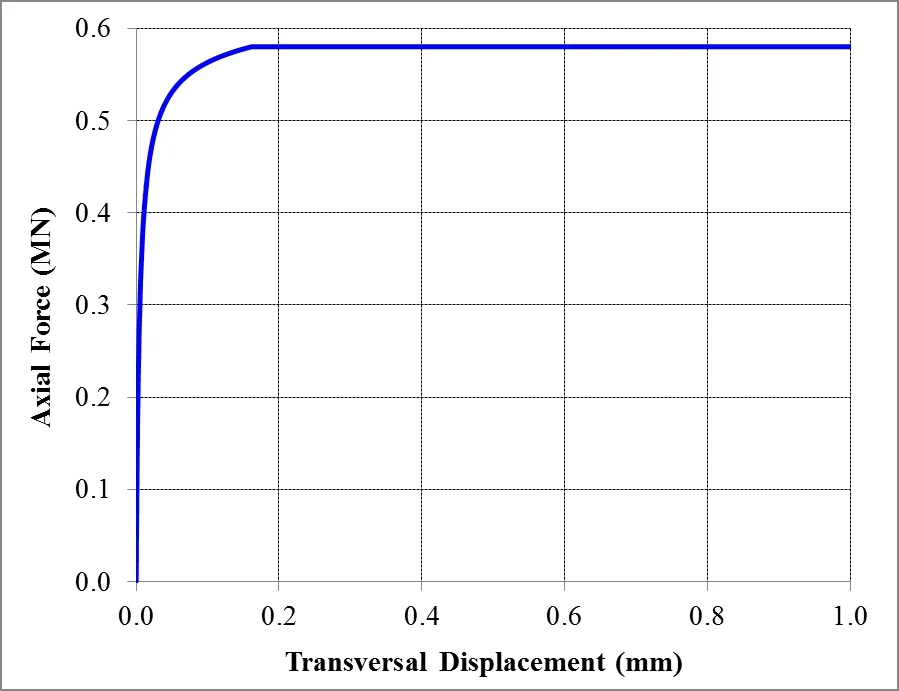
Figure 3:Axial compression load versus transversal displacement for homogeneous material properties and perfect mesh.

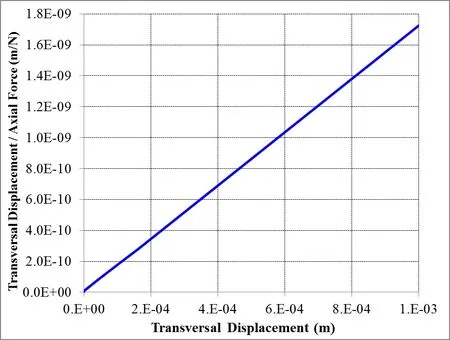
Figure 4:Southwell plot for homogeneous material properties and perfect mesh.

Observing Figure 3,it is noticed that the critical load estimated by DEM is aroundPcr=5.8×105N,which can also be estimated by the Southwell plot(Figure 4),through the inverse of the inclination,as beingPcr=5.8×105N.Therefore,it is concluded that as much the theoretical critical load as the critical load estimated by DEM resulting in approximately the same value,showing the good performance of the proposed method in estimating the buckling load.

Next,the bar is analyzed again simulating a static analysis, but now considering that the Young’s modulus and the mass density are assumed to be correlated Gaussian random fields of the spatial coordinates,according to the procedure proposed by Shinozuka and Deodatis(1996),with mean values of E(E)=2.0×1011Pa and E(ρ)=7850kg/m3and coefficient of variation equal to 10%for both material properties.The correlation lengths in the three directions were assumed to be the same and equal to 40L0,i.e.,2m for both material properties.In addition,perturbations in the DEM cubic mesh were introduced in this simulation,according to Equation(6),with a coefficient of variationCVpequal to 1%.

Figure 5 shows a graph of axial compression loadversusdisplacement in the free end in the direction perpendicular to the load application,while Figure 6 shows the corresponding Southwell plot.

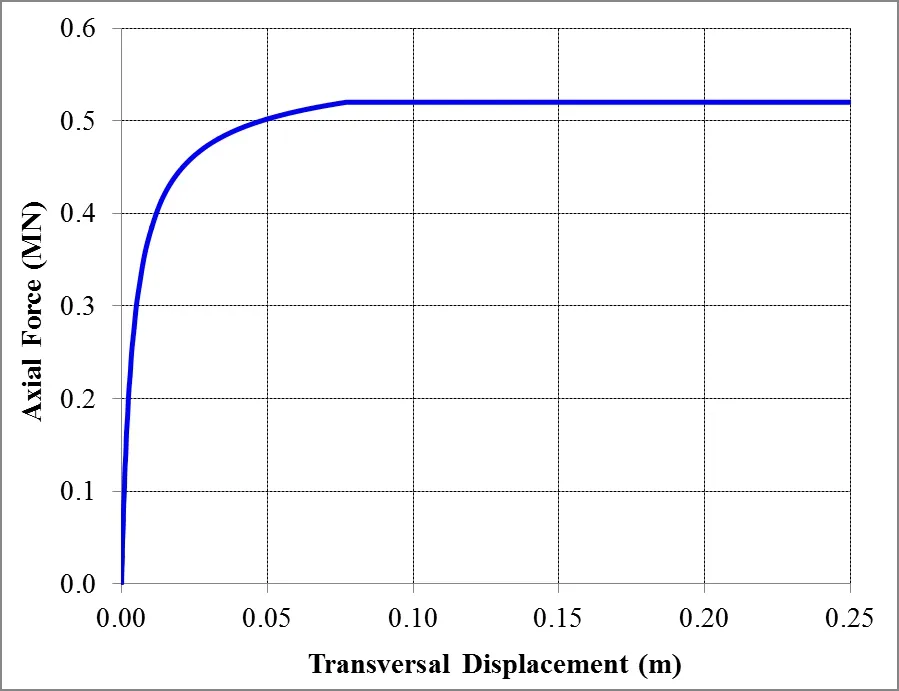
Figure 5:Axial compression load versus transversal displacement for nonhomogeneous material properties and imperfect mesh.

Observing Figures 5 and 6,it is noticed that the critical load estimated by DEM is aroundPcr=5.2×105N.As expected,due to non-homogeneous material properties and mesh imperfections,this critical buckling load is slightly lower(around 10%smaller)than the value for homogeneous material properties and without mesh imperfections.

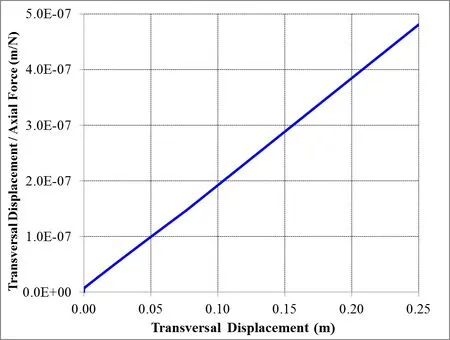
Figure 6:Southwell plot for non-homogeneous material properties and imperfect mesh.

4.3 Dynamic analysis

Now,the same bar is subjected to an impact axial load of amplitudeP0and durationtd.Again,initially it is supposed that the bar is homogenous and the mesh is not perturbed.The analytical result for the fundamental natural frequency of transversal vibration without axial load,applying Equation(3),resultsf0=3.3974Hz,i.e.,a fundamental period equal toT0=0.2943s.

Firstly,the durationtdof the impact load is assumed to be bigger than the vibration fundamental period of the bar(td＞T0)and the amplitudeP0of the impact load is assumed to be lower than the Euler critical buckling load(P0＜Pcr).

Figures 7 and 8 show the applied axial load and the transversal displacementversustime graphs,respectively.

As the duration of the impulsive load is larger than the fundamental period of the bar,it may be seen in Figure 8 that in the first 2 seconds,the bar vibrates with frequency of 1.89Hz,increasing to 3.40Hz(equal to the theoretical value obtained with Equation(3))as soon as the axial load is removed.These values are in accordance with Equation(2)forP0equal 4.0×105N.It is also possible to check that the maximum dynamic load factor is close to 2,which would be the theoretical lineal value without damping.

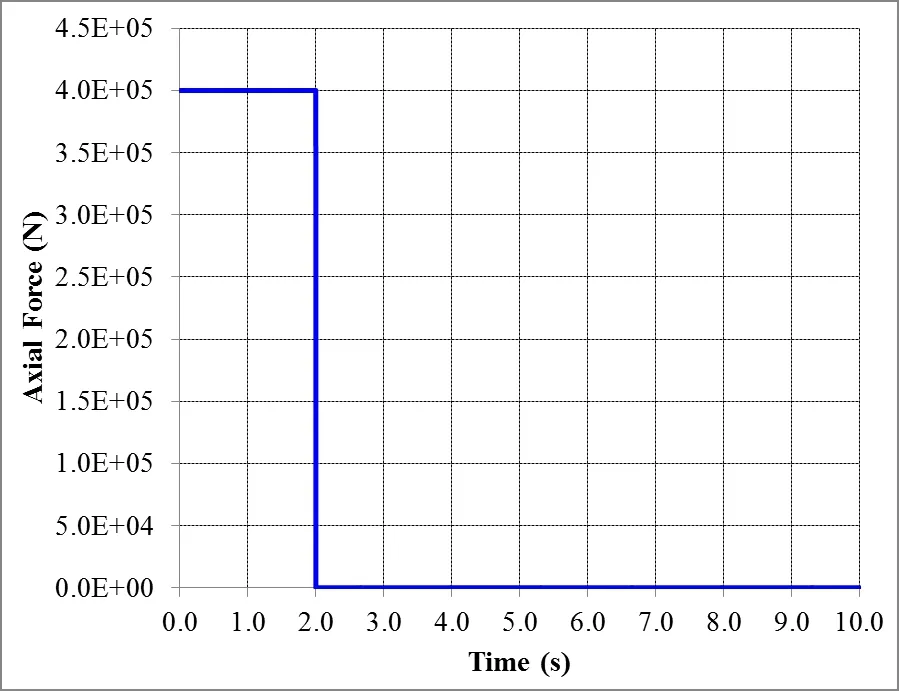
Figure 7:Applied axial impact load.

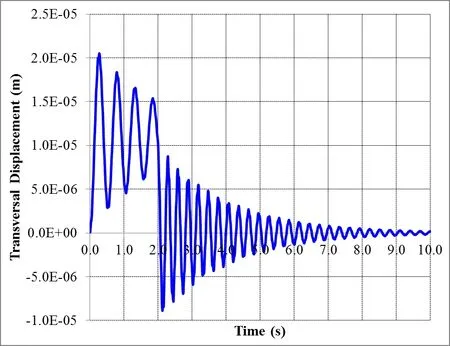
Figure 8:Transversal displacement versus time,for P0=4.0×105N and td=2.0s.

Next,the duration of the impact load was reduced to 0.29s,i.e.,lower than the fundamental period of the bar.The amplitude of the axial force was kept the same as before,i.e.,4.0×105N.Figure 9 shows the transversal displacementversustime graph.

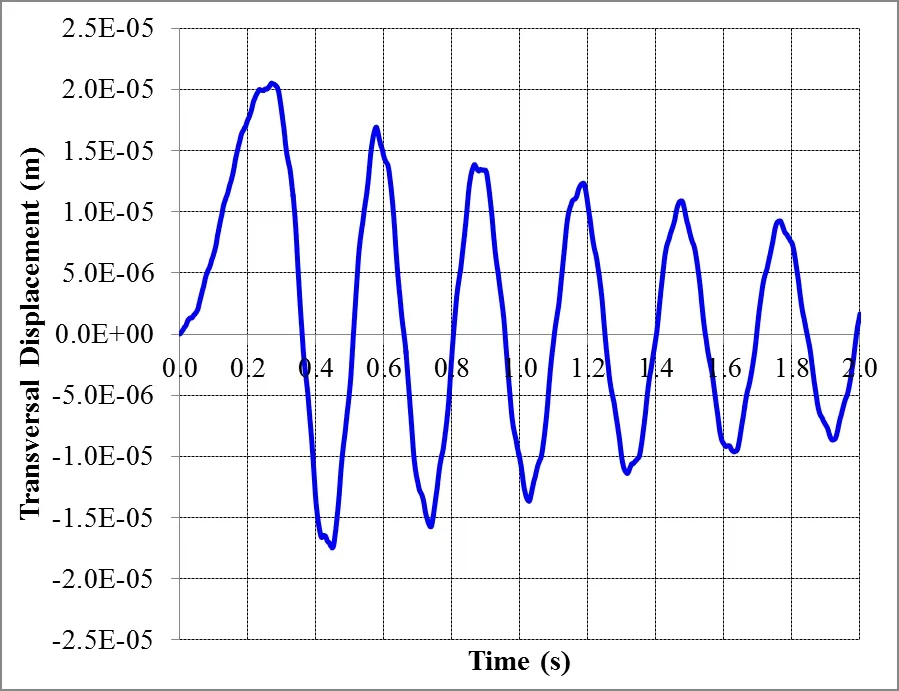
Figure 9:Transversal displacement versus time,for P0=4.0×105N and td=0.29s.

Now,the duration of the impact load was maintained equal to 0.29s,and the amplitude of the axial force was assumed to be 5.8×105N,i.e.,equal to the Euler critical buckling load.Figure 10 shows the transversal displacementversustime graph.

As may be verified in the graph of Figure 10,when the applied load is equal to the critical load,the period tends to infinite in the first 0.29s in which the load is applied,i.e.,frequency zero,confirming the result obtained by Equation(2).Additionally,it can be seen in Figures 9 and 10 that as soon as the axial load is removed(after 0.29s)the vibration frequency increases to 3.40Hz(equal to the theoretical value obtained with Equation(3)).

As expected,the previous results confirm the good performance of the proposed methodology in the static and dynamic instability analyses of homogenous bars without geometrical imperfections.

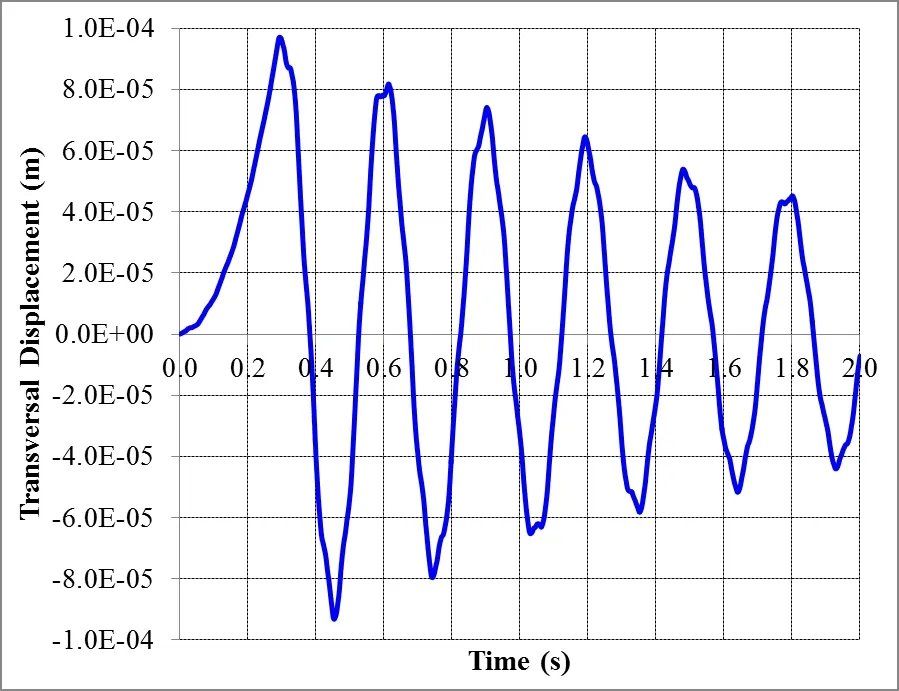
Figure 10:Transversal displacement versus time,for P0=5.8×105N andtd=0.29s.

Figure 11:Transversal maximum displacement versus axial force for non-homogeneous material properties and imperfect mesh.

Thus,now the DEM is used to carry out dynamic instability analyses of non-homogeneous bars considering that the Young’s modulus and the mass density are assumed to be correlated Gaussian random fields of the spatial coordinates with mean values of E(E)=2.0×1011Pa and E(ρ)=7850kg/m3and coefficient of variation equal to 10%for both material properties.The correlation lengths in the three directions were assumed to be the same and equal to 40L0,i.e.,2m for both material properties.In addition,perturbations in the DEM cubic mesh were introduced in these simulations,according to Equation(6),with a coefficient of variationCVpequal to 1%.

Figure 11summarizes the results of these several dynamic simulations, showing the transversal maximum displacementversusaxial force(fortd=0.29s),which could serve as a preliminary criterion of decision on the occurrence or not of dynamic instability,using,for instance,the well-known Budiansky-Hutchinson(1966)criterion.

5 Conclusions

This paper proposed a numerical methodology to analyze dynamic instability of straight bars subjected to impulsive axial loads based on the truss-like Discrete Element Method(DEM).The proposed method is able to handle both static and dynamic loads and also with both ideal and non-ideal bars.In the DEM,the integration of the equations of motion is carried out in an explicit way,by central finite differences,allowing the consideration of large displacements and nonlinearities easily.

Initially the DEM was applied to solve static and dynamic instability problems of ideal bars,i.e.,homogeneous bars without geometrical imperfections.These results were compared with analytical solutions,showing the good performance of the proposed methodology.After that,mesh imperfections and also the possibility to assume that any material property to be correlated Gaussian random fields of the spatial coordinates were implemented.These improvements led the DEM to be a tool that is able to simulate more realistic cases,i.e.,non-ideal members,in which the bars have imperfections and can also be non-homogeneous.

Finally,the proposed methodology could be used by designers as a tool of easy use for estimating the dynamic buckling load.

Acknowledgement:The authors acknowledge the financial support of CNPq and CAPES.

Ari-Gur,J.;Weller,T.;Singer,J.(1978):Experimental studies of columns under axial impact.Report TAE 346,Department of Aeronautical Engineering,Technion-Israel Institute of Technology,Haifa.Israel.

Ari-Gur,J.;Weller,T.;Singer,J.(1982):Experimental and theoretical studies of columns under axial impact.Int.J.Solids Struct.,vol.18,no.7,pp.619-641.

Ari-Gur,J.;Elishakoff,I.(1997):Dynamic instability of a transversely isotropic column subjected to a compression pulse.Computers&Structures,vol.62,no.5,pp.811-815.

Budiansky,B.;Hutchinson,J.W.(1966):Dynamic buckling of imperfection sensitive structures.Proc.11thInt.Congr.of Applied Mechanics,Munich.Springer,Berlin,pp.636-451.

Dalguer,L.A.;Irikura,K.;Riera,J.D.(2003):Simulation of tensile crack generation by three-dimensional dynamic shear rupture propagation during an earthquake.Journal of Geophysical Research,vol.108,no.B3,pp.2144.

Davidson,J.F.(1953):Buckling of struts under dynamic loading.Journal of the Mechanics and Physics of Solids,vol.2,pp.54-66.

Del Prado,Z.J.G.N.;Carvalho,E.C.;Gonçalves,P.B.(2010):Dynamic stability of imperfect cable stayed masts.Asociación Argentina de Mecánica Computacional.Mecánica Computacional,Vol XXIX,pp.647-658,Buenos Aires,Argentina,15-18 November 2010.

Fereidooni,A.;Behdinan K.;Fawaz,Z.(2008):Dynamics of Laminated Composite Beams-Instability Behavior.International Conference on Computational&Experimental Engineering and Sciences,vol.5,no.3,pp.157-162.

Huffington Jr.,N.J.(1963):Response of elastic columns to axial pulse loading.AIAA Journal,vol.1,no.9,pp.2099-2104.

Hutchinson,J.W.;Budiansky,B.(1966):Dynamic buckling estimates.AIAA Journal,vol.4,no.3,pp.525-530.

Iturrioz,I.;Miguel,L.F.F.;Riera,J.D.(2009):Dynamic fracture analysis of concrete or rock plates by means of the Discrete Element Method.Latin American Journal of Solids and Structures,vol.6,pp.229-245.

Kaminski Jr.,J.;Riera,J.D.;Menezes,R.C.R.;Miguel,L.F.F.(2008):Model uncertainty in the assessment of transmission line towers subjected to cable rupture.Engineering Structures,vol.30,pp.2935-2944.

Koning,C.;Taub,J.(1933):Impact buckling of thin bars in the elastic range hinged at both ends.Luftfahrtforschung,vol.10,no.2,pp.55.

Lindberg,H.E.;Florence,A.L.(1987):Dynamic Pulse Buckling.Martinus Nijhoff,Dordrecht,Ch.2.

Miguel,L.F.F.;Riera,J.D.;Dalguer,L.A.(2006):Macro constitutive law for rupture dynamics derived from micro constitutive law measured in laboratory.Geophysical Research Letters,vol.33,L03302.

Miguel,L.F.F.;Riera,J.D.(2007):A constitutive criterion for the fault: modified velocity-weakening law.Bulletin of the Seismological Society of America,vol.97,no.3,pp.915-925.

Miguel,L.F.F.;Riera,J.D.;Iturrioz,I.(2008):influence of size on the constitutive equations of concrete or rock dowels.International Journal for Numerical and Analytical Methods in Geomechanics,vol.32,no.15,pp.1857-1881.

Miguel,L.F.F.;Iturrioz,I.;Riera,J.D.(2010):Size effects and mesh independence in Dynamic Fracture Analysis of Brittle Materials.Computer Modeling in Engineering&Sciences,vol.56,no.1,pp.1-16.

Motamarri,P.;Suryanarayan,S.(2012):unified analytical solution for dynamic elastic buckling of beams for various boundary conditions and loading rates.International Journal of Mechanical Sciences,vol.56,pp.60-69.

Nayfeh,A.H.;Hefzy,M.S.(1978):Continuum modeling of three-dimensional truss-like space structures.AIAA Journal,vol.16,no.8,pp.779-787.

Riera,J.D.;Iturrioz,I.(1998):Discrete elements model for evaluating impact and impulsive response of reinforced concrete plates and shells subjected to impulsive loading.Nuclear Engineering and Design,vol.179,pp.135-144.

Riera,J.D.;Miguel,L.F.F.;Iturrioz,I.(2011):Strength of brittle materials under high strain rates in DEM simulations.Computer Modeling in Engineering&Sciences,vol.82,no.2,pp.113-136.

Riera,J.D.;Miguel,L.F.F.;Iturrioz,I.(2014):Assessment of Brazilian tensile test by means of the truss-like Discrete Element Method(DEM)with imperfect mesh.Engineering Structures,vol.81,pp.10-21.

Rios,R.D.;Riera,J.D.(2004):Size effects in the analysis of reinforced concrete structures.Engineering Structures,vol.26,no.8,pp.1115-1125.

Shinozuka,M.;Deodatis,G.(1996):Simulation of multi-dimensional gaussian stochastic fields by spectral representation.Applied Mechanics Review,vol.49,no.1,pp.29-53.

Simitses,G.J.(1990):Dynamic Stability of Suddenly Loaded Structures.Springer,New York,Ch.10.

Stojanovi´c,V.;Kozi´c,P.;Pavlovi´c,R.;Janevski,G.(2011):Effect of rotary inertia and shear on vibration and buckling of a double beam system under compressive axial loading.Arch.Appl.Mech.,vol.81,no.12,pp.1993-2005.

Teter,A.;Kolakowski,Z.(2013):Coupled dynamic buckling of thin-walled composite columns with open cross-sections.Composite Structures,vol.95,pp.28-34.

Trikha,M.;Gopalakrishnan,S.;Mahapatra,D.R.;Pandiyan,R.(2009):Dynamic Instabilities in Slender Space Launch Vehicles under Propulsive Thrust and Aerodynamic Forces.Computer Modeling in Engineering&Sciences,vol.45,no.2,pp.97-140.

Vincent,P.;Huet,C.;Charbonneau,M.;Guilbault,P.;Lapointe,M.;Banville,D.;McClure,G.(2004):Testing and numerical simulation of overhead transmission line dynamics under component failure conditions.CIGRÉ Session 2004,Paris.

Yeh,M.K.;Liu,C.S.;Chen,C.C.(2014):Dynamic Instability of Rectangular Composite Plates under Parametric Excitation.Computers,Materials&Continua,vol.39,no.1,pp.3-20.

1Prof.Dr.,Department of Mechanical Engineering,UFRGS,Porto Alegre,RS,Brazil.

E-mail:letffm@ufrgs.br

2Prof.Dr.,Department of Civil Engineering,UFSC,Florianópolis,SC,Brazil.

E-mail:leandro.miguel@ufsc.br

3Prof.Dr.,Department of Structures and Civil Construction,UFSM,Santa Maria,RS,Brazil.

E-mail:jkj@ufsm.br thod,Impulsive Load,Stochastic Fields,Mesh Imperfections.