A Meshless LBIE/LRBF Method for Solving the Nonlinear Fisher Equation:Application to Bone Healing

,4

1 Introduction

Linear and nonlinear transient diffusion is associated with problems dealing with heat conduction in materials,structures and tissues,mass transfer,surface annealing,welding and drilling of metals, chloride diffusion in concrete, pattern formationin population dynamics and solidification processes.In the context of biology and for the difficult and complicated problem of cell proliferation and migration a mathematical model that has been widely used for the simulation of those processes is the nonlinear partial differential equation proposed by[Fisher(1937)]. Specifically,for the case of bone regeneration unforced and/or forced Fisher partial differential equation has been employed in order to model the bone healing process and predict relative experimental observations[Isaksson, Donkelaar,Huiskes and Ito(2008);Garcia-Aznar,Kuiper,Gomez-Benito,Doblare and Richardson(2007);Andreykiv,Van Keuler and Prendergast(2008);Gunzburger,Hou and Zhu(2005);Moreo,Gaffney,Garcia-Aznar and Doblare(2010);Sengers,Please, Oreffo(2007)].

Due to nonlinear form of Fisher’s equation,analytical solutions are very difficult to be performed in two or three dimensions and when they exist are con fined to special cases and simple geometries[Petrovskii and Shigesada(2001)].For this reason resort should be made to numerical methods,which are able to solve such problems.In the rich literature of the numerical methods that are able to treat nonlinear diffusion partial differential equations one can mention the Finite Element Method(FEM)[Garcia-Aznar,Kuiper,Gomez-Benito,Doblare and Richardson(2007)],the Finite Differences Method(FDM)[Khiari and Omrani(2011)],the Finite Volume Method(FVM)[Prokharau,Vermolen and Garcia-Aznar(2013)],the Dual Reciprocity Boundary Element Method(DR-BEM)[Guo,Chen and Gao(2012)],the Domain-BEM[Mohammadi,Hematiyan and Marin(2010)]and the Analog-BEM[Katsikadelis and Nerantzaki(1999)].The main problem with FEM,FDM and FVM is their requirement for domain discretization,which could be problematic or time consuming for complicated geometries,while the boundary methods such as DR-BEM and Analog-BEM are associated with very time consuming fully populated and non-symmetric matrices.

The last fifteen years,meshless methods have received considerable attention since they are able to treat efficiently nonlinear problems without meshing requirements.In the area of linear and nonlinear diffusion problems one has to mention the Meshless Local Petrov-Galerkin(MLPG)method[Lin and Atluri(2000);Sladek,Sladek,Tan and Atluri(2008);Chen and Liew(2011);Mirzaei and Dehgham(2011)]the Local Boundary Integral Equation(LBIE)method[Sladek,Sladek and Zhang(2004)],[Shirzadi,Sladek, Sladek(2013);Popov and Bui(2010)],the Meshfree Point Collocation Method(MPCM) [Bourantas and Burganos(2013);Sarler and Vertnik(2006)],[Trobec,Kosec,Sterk and Sarler(2012)]and the Meshless local radial point interpolation(MLRPI)method [Shivanian(2013)].More details on meshless methods one can find in the books of Atluri and Shen[Atluri and Shen(2002);Atluri(2004);Li and Liu(2007)]and in the very recent review work of[Sladek,Stanak,Han,Sladek,Atluri(2013);Atluri and Zhu(1998);Zhu,Zhang and Atluri(1998,1999)]were the first who proposed the meshless MLPG and LBIE methods,respectively,as a simple and less-costly alternative to the FEM and BEM,respectively.Their methods are characterized as meshless methods because the interpolation is accomplished through randomly distributed points covering the domain of interest and characterized by no-connectivity requirements.The fields at the local and global boundaries as well as in the interior of the subdomains are usually approximated by the Moving Least Squares(MLS)approximation scheme.The local nature of the sub-domains leads to a final linear system of equations the coefficient matrix of which is sparse and not fully populated.

After the pioneering work of[Zhu,Zhang and Atluri(1998)],meshless LBIE method have received considerable attention due to its accuracy as integral equation method and its flexibility to avoid any kind of mesh.Very recently[Sellountos,Sequeira and Polyzos(2009)]proposed a stable,accurate and very simple meshless LBIE method for solving elastostatic problems,which utilizes an efficient Local Radial Basis Functions(LRBF) interpolation scheme[Sellountos,Sequeira and Polyzos(2010);Hardy(1990)]instead of MLS approximation and combines techniques applying in both BEM and LBIE method.At the boundaries of local domains tractions are eliminated with the aid of the companion solution of elastostatic equation[Li and Liu(2007)],while at the global boundary displacements and tractions are treated as independent variables.All the integrals at local and global boundaries are evaluated as in the case of a BEM formulation and the displacement nodal values are interpolated through the LRBFs.In that way,the LBIE/LRBF method proposed by[Sellountos,Polyzos and Atluri(2012)]solves the elastostatic problem very efficiently avoiding derivatives of LRBFs and concluding to a final system of algebraic equations with banded coefficient matrix.

In the present work,that methodology is implemented for the case of two dimensional(2D)transient diffusion problems described by the nonlinear Fisher equation.Then the new LBIE/LRBF method is employed to provide numerical predictions for cell proliferation in a 2D model of fractured bone.As in[Sellountos,Sequeira and Polyzos(2009)],at each internal or boundary point a circular support domain is centered and the LBIE valid for the potential field and its flux is assigned.Both LBIEs are derived with the aid of Laplace fundamental solution,thus containing volume integrals coming from transient and nonlinear terms that act as internal sources.On the local circular boundaries,all the integrals that contain the fluxes of the potential field are eliminated via companion solutions derived for the needs of the present work.The circular local domains are sectored into subregions and their boundary is discretized into line quadratic elements that in turn introduce a number of“temporary”nodal points which,however,have not any relation with the initially considered nodal points.Then,all the involved surface and volume integrals are very accurately evaluated with the aid of the integration technique proposed by[Gao(2002,2005)],while the potential fields defined at the“temporary”nodes are interpolated through the LRBF scheme illustrated in[Sellountos,Sequeira and Polyzos(2009)].In that way,the final system of algebraic equations is derived very efficiently without the use of derivatives of the LRBF interpolants.The treatment of the nonlinearity is accomplished with the aid of the Newton-Raphson scheme and the problem is solved without the need of any derivative of the utilized LRBFs.It should be mentioned here that the idea of using “temporary”nodal points was first proposed by[Popov and Bui(2010)]and that was unintended ignored in[Sellountos,Polyzos and Atluri(2012)].However,the LBIE methodology of Popov and Bui is completely different to the ones proposed in[Sellountos,Polyzos and Atluri(2012)]and here.

The paper is organized as follows:The LBIEs valid for potentials and their fluxes are explicitly derived in the next section.The LRBF interpolation scheme employed in the present method is illustrated in section 3.The numerical implementation of the proposed LBIE/LRBF methodology for solving the Fisher equation is presented in section 4,while representative benchmark problems that demonstrate the accuracy of the method are provided in section 5.Finally,the LBIE/LRBF method is employed to solve the Fisher equation for a 2D model dealing with cell proliferation in a bone healing process.The obtained results are demonstrated and discussed in section 6.

2 LBIEs for Fisher’s non-linear transient diffusion equation

In this section the LBIEs used in the present method are illustrated.Consider a two dimensional domain V surrounded by a surface S and a concentration or population density function φ(x1,x2,t)at the spatial position(x1,x2)and time t.According to Fisher equation,the field φ(x1,x2,t)satisfies the partial differential equation:

where D1,D2,a are positive constants depending on the nature of the problem and∂i,∂tpartial derivatives with respect to spatial coordinate xi,i=1,2 and time,respectively.

The boundary conditions are assumed to be

with n denoting the unit vector normal to the global boundary,φ0,q0prescribed functions and

Making use of the finite-differences scheme

and ignoring higher order terms,the governing equation(1)obtains the form

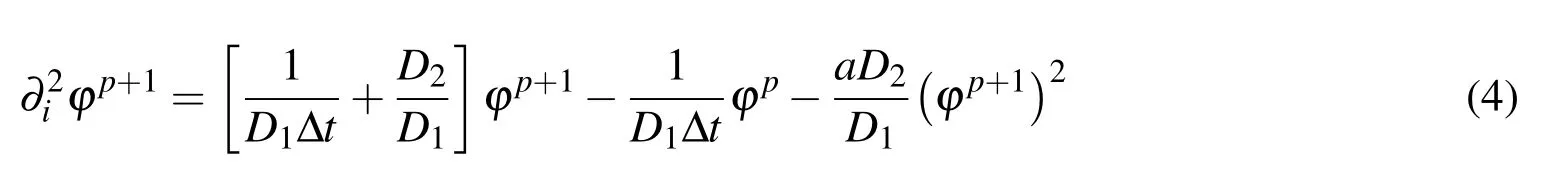
Utilizing the fundamental solution of Laplace equation and applying Green’s integral identity one obtains the following integral equation

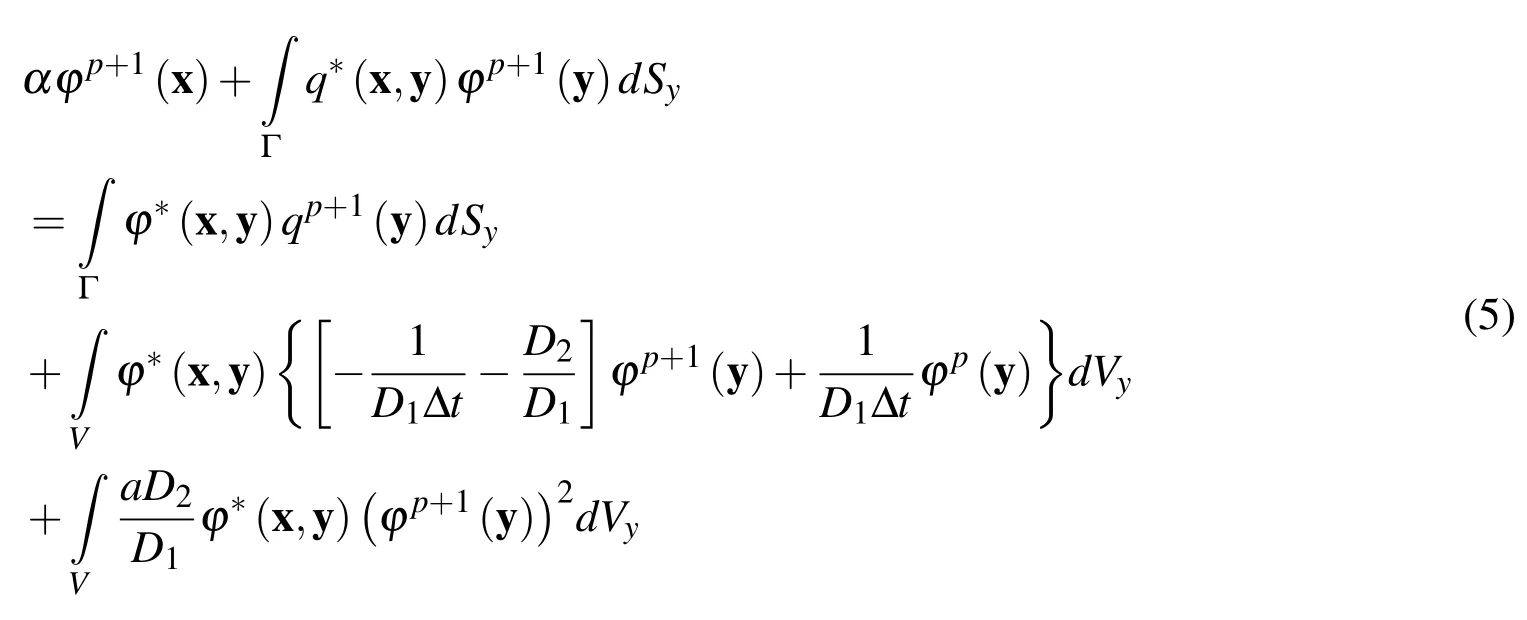
where the coefficient α takes the value 0.5 whenx∈S and S being a smooth boundary and the value 1 whenx∈V,while the kernels φ∗,q∗have the form

A group of N randomly distributed pointsx(k),k=1,..,N that cover the domain of interest V are considered,while the global boundary Sφ∪Sq≡S is defined through a BEM mesh with Z totally nodal points.At any pointx(k)a circular domain Ω(k)(with boundary∂Ω(k))is centered,called support domain ofx(k)and illustrated in Figure 1.

Employing Green’s second identity for the domain being between the boundaries S and∂Ω(k),the integral representation(5)obtains the form:

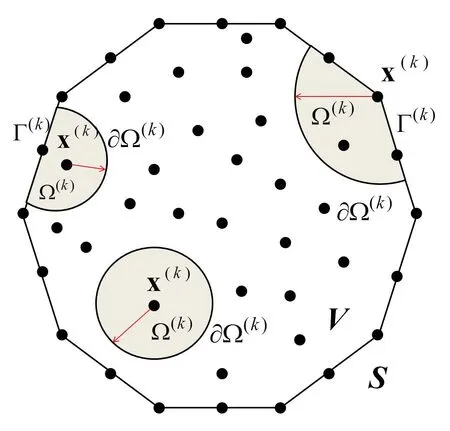
Figure 1:Local domains and local boundaries used for the LBIE representation of density function φ(x(k)).

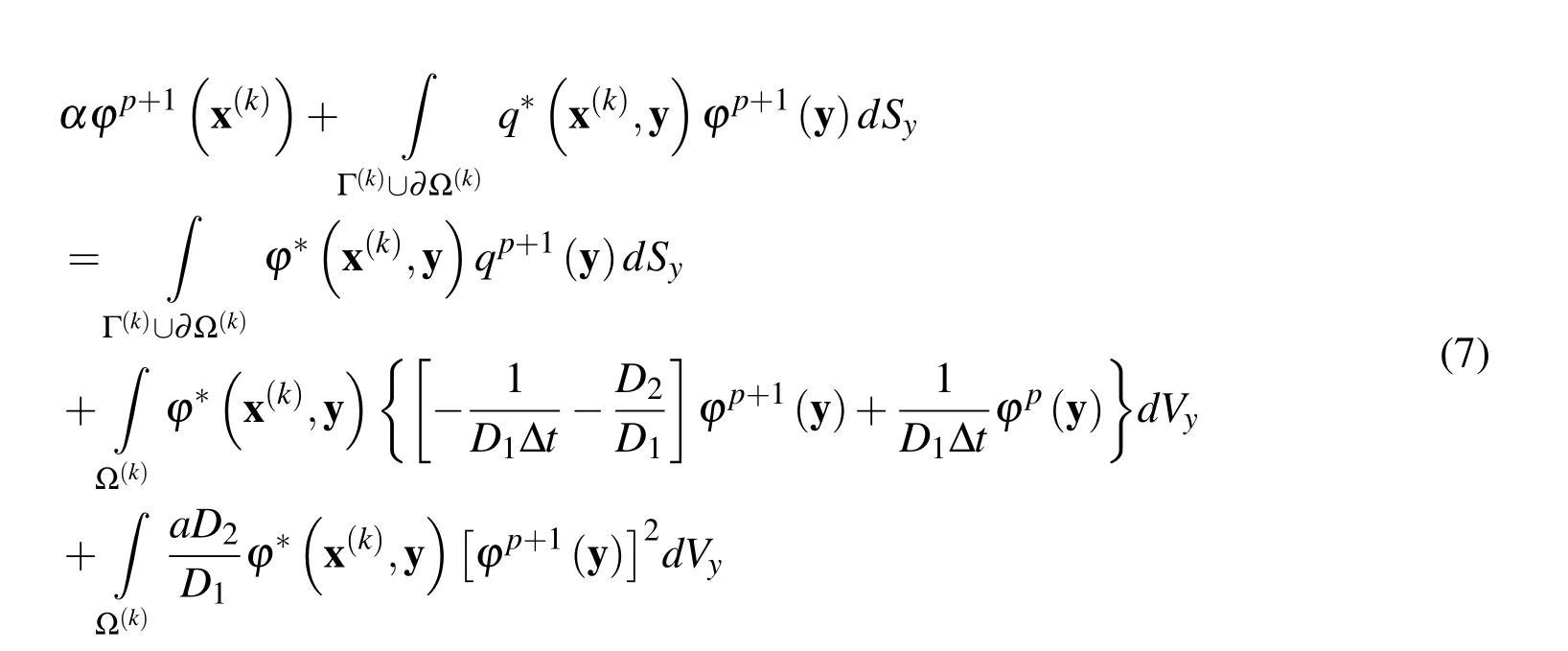
with Γ(k)being the part of the global boundary intersected by the circular support domain of pointx(k)(Fig.1).

The coefficient α is equal to 1 for internal points and 1/2 for points lying on the global boundary Γ with smooth tangent.As it has been already mentioned,in the present formulation,boundary points are imposed with the aid of a BEM mesh.Thus,in case of a non-smooth boundary partially discontinuous elements at both sides of a corner are considered.Consequently,the coefficient α is always equal to 0.5 for all the boundary pointsx(k).

In order to get rid of fluxes at the local boundary∂Ω(k)the companion solution of Laplace equation can be utilized[Atluri(2004)]and Eq.(7)becomes

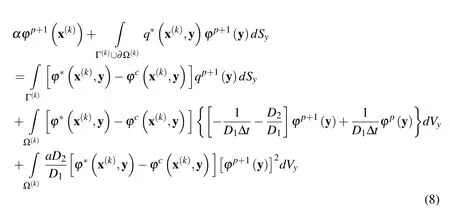
where φcrepresents the companion solutionlnrkwith rkdenoting the radius of the support domain of pointx(k).

An integral representation for the gradient of φp+1can be obtained by applying the gradient operator on Eq.(7),i.e.

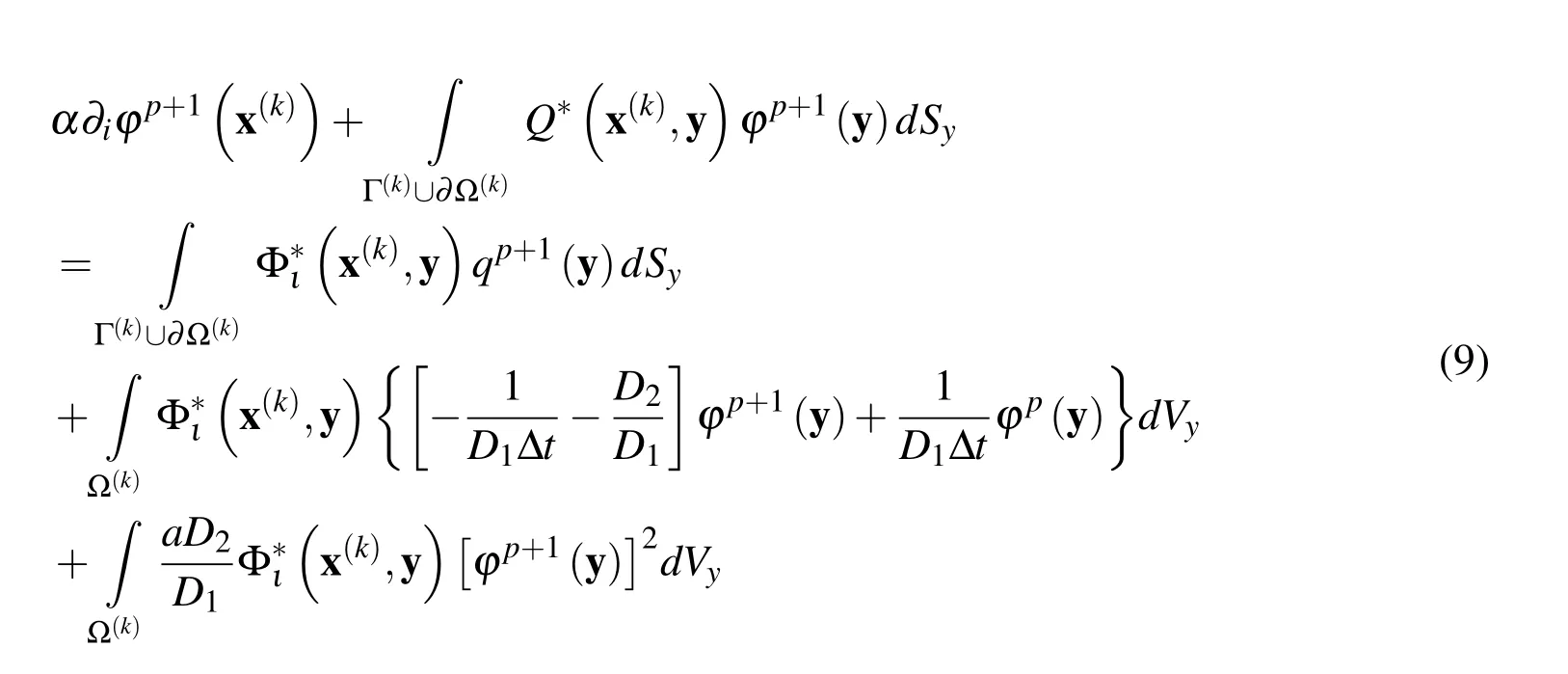
The integral defined at the local boundary∂Ω(k)and containing the fluxes qp+1can be eliminated with the aid of a new companion solution derived in Appendix A.

Thus,following the procedure described in Appendix A Eq.(9)can be written as

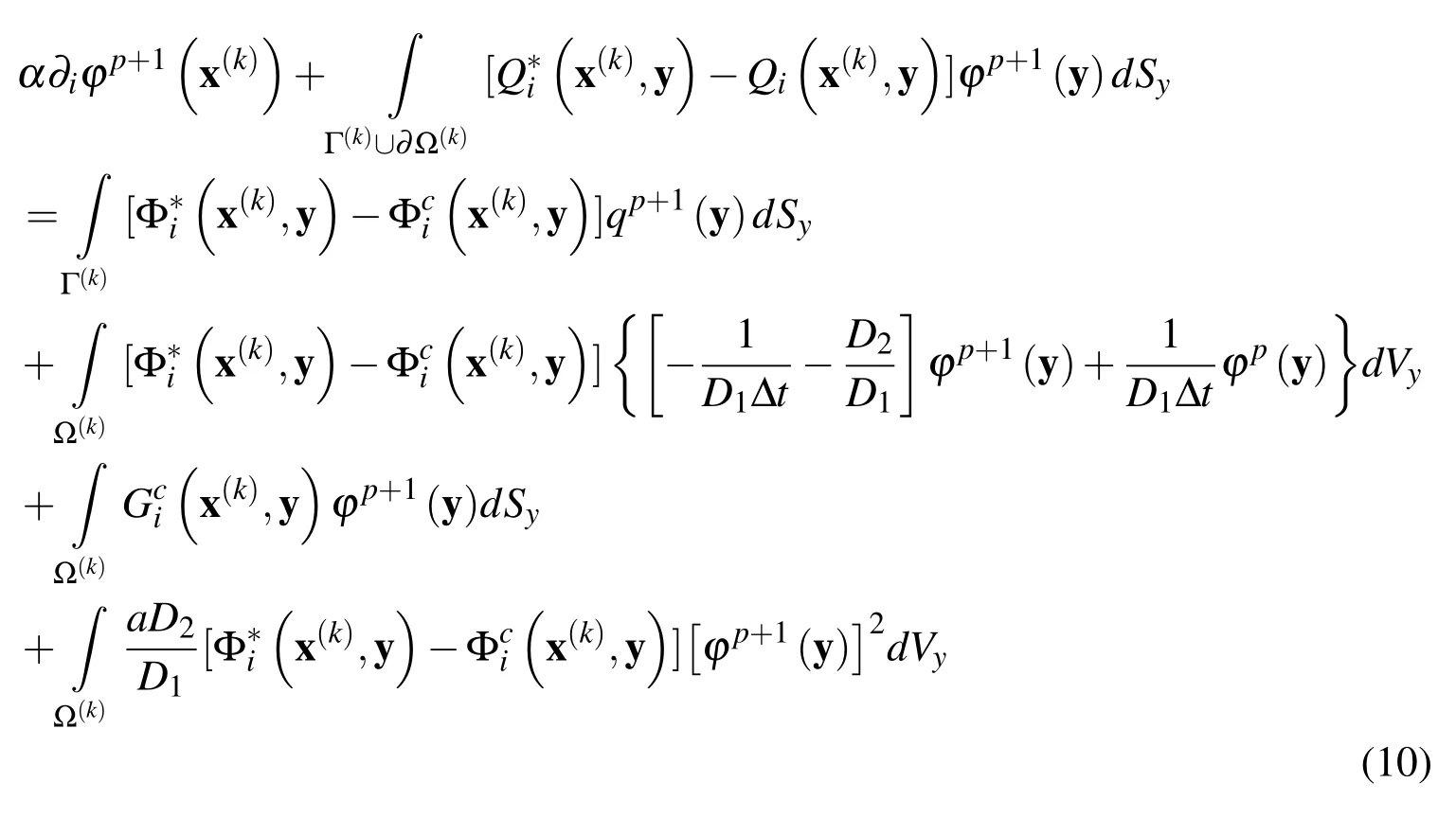
where

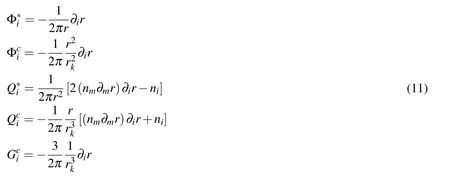
The integral equations(8)and(10)represent the LBIEs for the(p+1)-step fieldsand,respectively at any interior and boundary point of the analyzed domain.

3 The LRBF interpolation scheme

In the present section the LRBF interpolation scheme employed in the present work is illustrated.Consider a domain V surrounded by a boundary Γ covered by arbitrarily distributed nodal points

as shown in Fig.1.Each nodal pointx(k)is considered as the centre of a small circular domain Ωkof radius rkcalled support domain ofx(k).All support domains of a group of adjacent nodal points that satisfy the condition

form a domain called domain of influence of pointx(k)(Fig.2).The support domains of all the considered internal and boundary points are overlapping circles that cover completely the domain of interest.The support domains of the nodal points that contain a pointxform the domain of definition of pointx,also illustrated in Fig.2

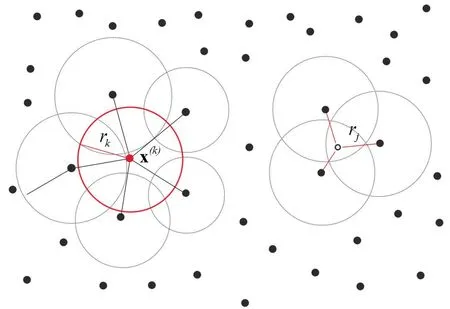
Figure 2:Domain of influence of the point x(j)and domain of definition of point x.

At any pointxof Ω,the interpolation of the unknown field φ (x),is accomplished by the relation

or

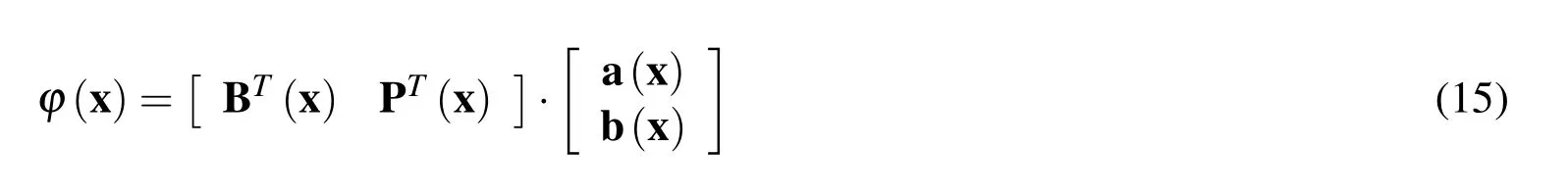
where

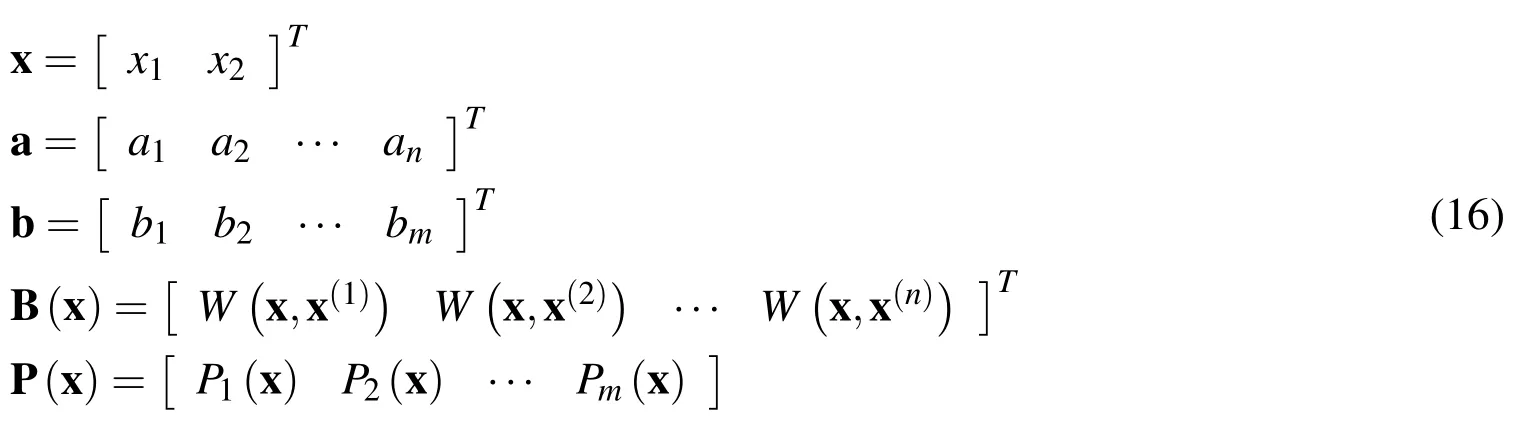
with n representing the total number of nodal points belonging to the domain of definition of pointxand m the number of complete polynomials with m＜n.The vectorsaandbstand for unknown coefficient vectors that depend on the location of the nodal points belonging to the domain of definition of pointx.P(x)is a vector containing the monomial basis,i.e.

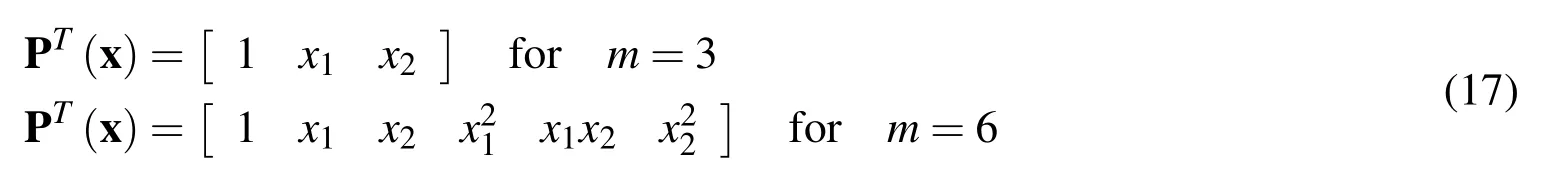
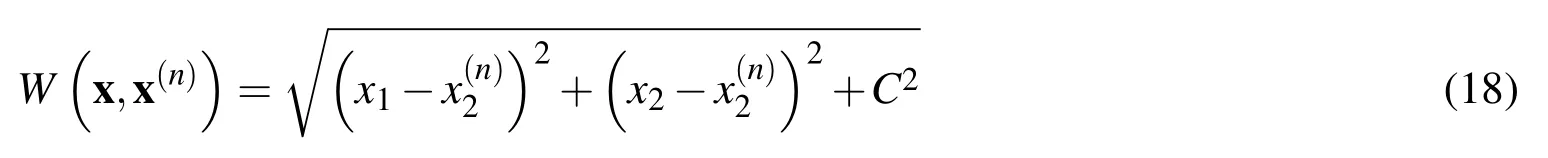
For the domain of definition ofx,C is a constant the value of which is taken equal to[Hardy(1990)]

with dibeing the distance between every nodal point of the domain of definition ofxand its closest nodal neighbor.

The definition of the unknown vectorsaandbis accomplished by imposing an interpolation passing of Eq.(15)through all nodal points x(n),i.e.

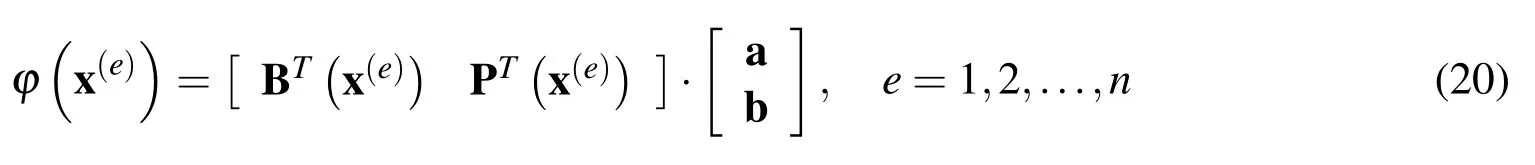
and considering the extra system of algebraic equations

Thus,the following system of equations is formed:

where

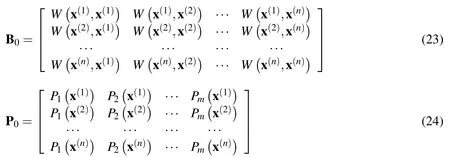
and

whereAis the symmetric matrix

Finally,the interpolation Eq.(15)obtains the form

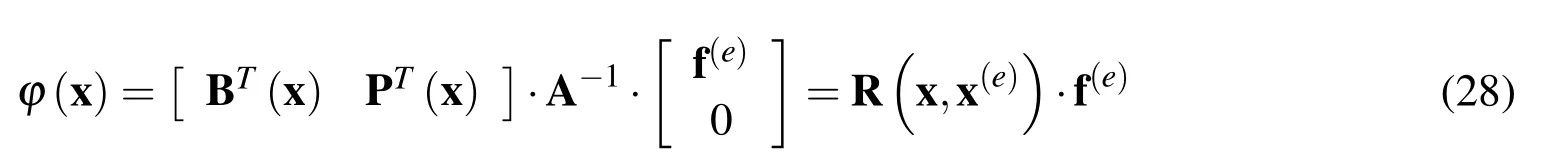
where

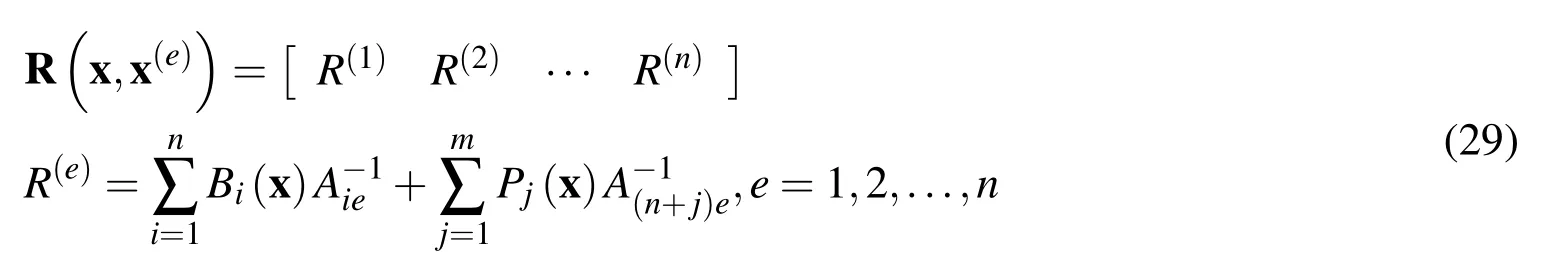
The LRBF shape functions(29)depend uniquely on the distribution of scattered nodes belonging to the support domain of the point where the field is interpolated.The positive definitiveness of the just described LRBFs is accomplished with the use of the additional polynomial term in Eq.(14)and the homogeneous constraint condition(21).More details on the LRBFs one can find in the book of[Buhmann(2004)]and in the representative works of[Sellountos and Sequeira(2008a,2008b);Wang and Liu(2002);Gilhooley,Xiao,Batra,McCarthy and Gillespie(2008)]and [Bourantas, Skouras,Loukopoulos,Nikiforidis(2010)].

4 Numerical implementation of the proposed LBIE/LRBF method

In this section the numerical implementation of the proposed LBIE/LRBF methodology is reported.

As it has been explained in section 2,the function φp+1(x(k))defined at any internal pointx(k)with support domain that does not intersect the global boundary,admits a LBIE of the form

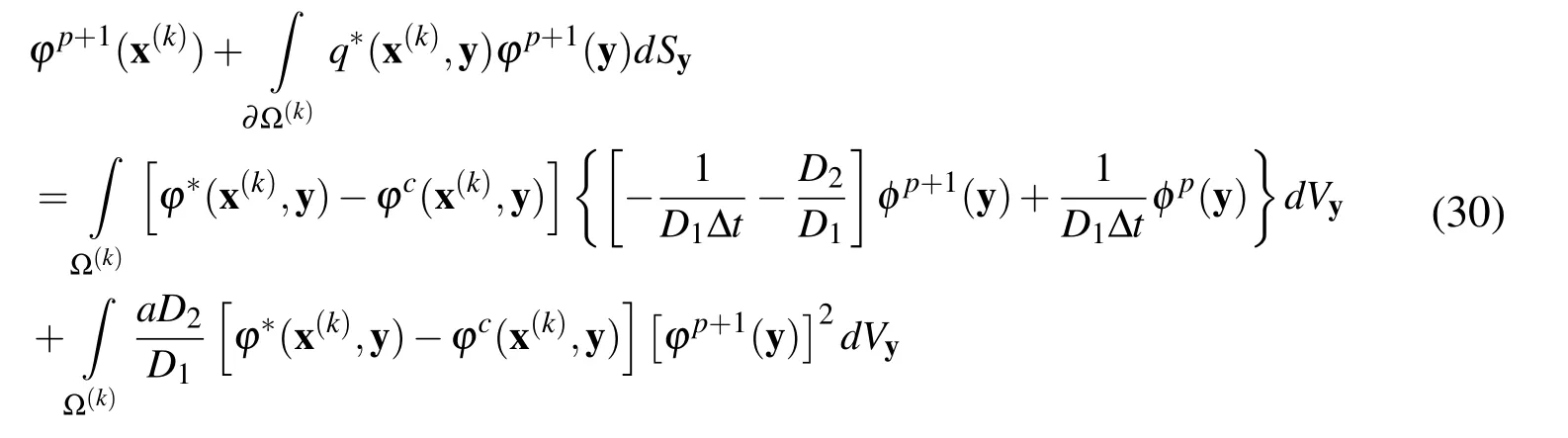
Since Ω(k)represents a circular domain,the above LBIE can be written in polar coordinated as[Gao(2002,2005)].

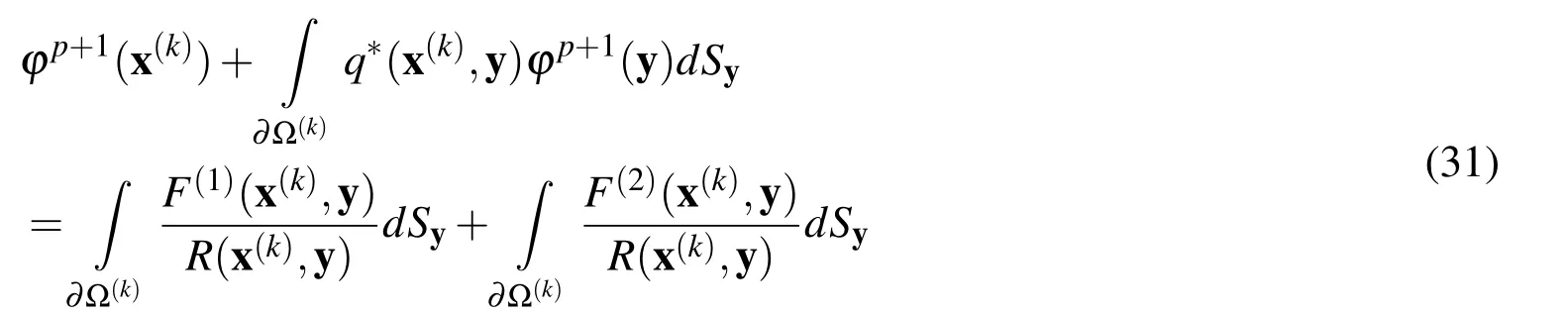
where

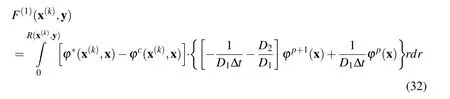
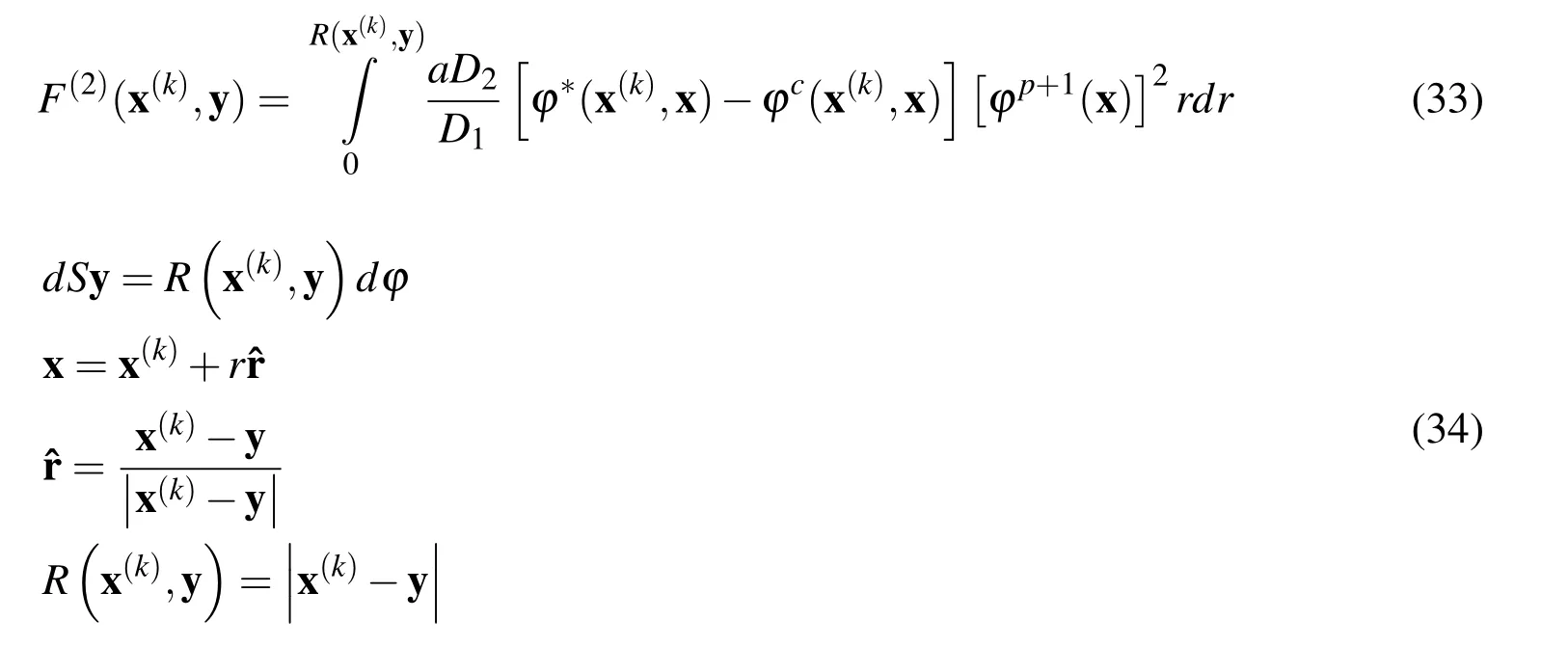
Considering,just for demonstration purposes,4 quadratic line elements across the circumferential direction and one quadratic element in radial direction,the LBIE(31)obtains the form

where N(bn),N(m)are the shape functions corresponding to quadratic line elements in the circumferential and radial direction,respectively,Jband Jmare the corresponding Jacobians of the transformation from the global to the local coordinate systems ξ and the vectorx(mbn)represents all the radial and circumferential nodes indicated with open circles in Fig.3.

It should be noticed here that those pointsx(mbn)have not any relation with the initially considered nodal points,which in Fig.3 are indicated with the full circles.Thus,in Fig.3 the full circles represent the nodal points used for the meshless procedure while the open circles represent the“temporary”nodal points,which are the same for any non-intersected support domain.Considering the 16 “temporary”

nodal points of Fig.3(a),Eq.(33)obtains the form

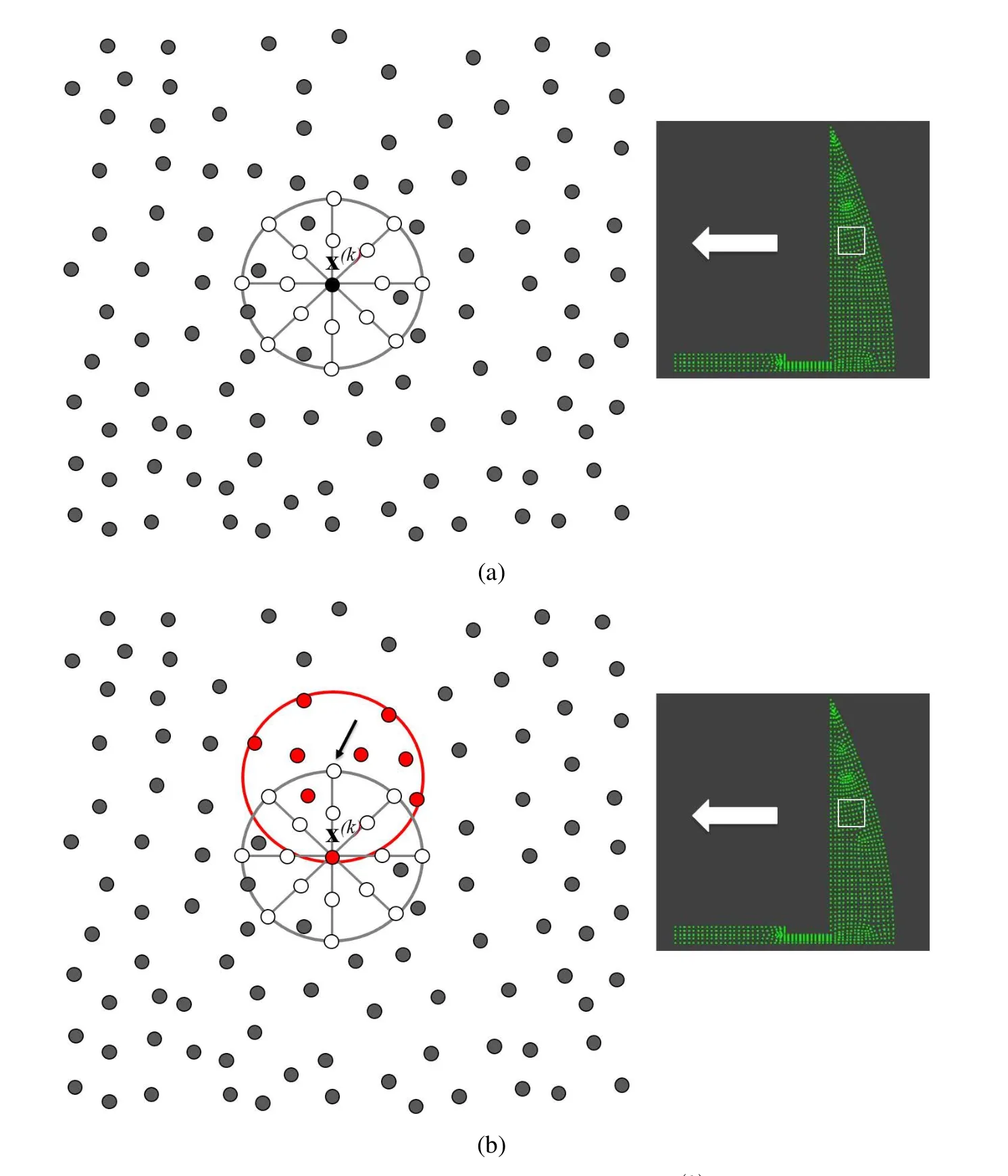
Figure 3:(a)The support domain of an internal point x(k)sectored and discetized by line quadratic elements in the circumferential and radial direction.The full circles stand for the nodal points used for the meshless treatment of the structure,while the open circles represent the“temporary”nodal points.(b)The field at each“temporary”nodal point is interpolated via LRBFs defined via the nodal points(red points)belonging in the support domain(red circle)of the“temporary”nodal point indicated by the arrow.

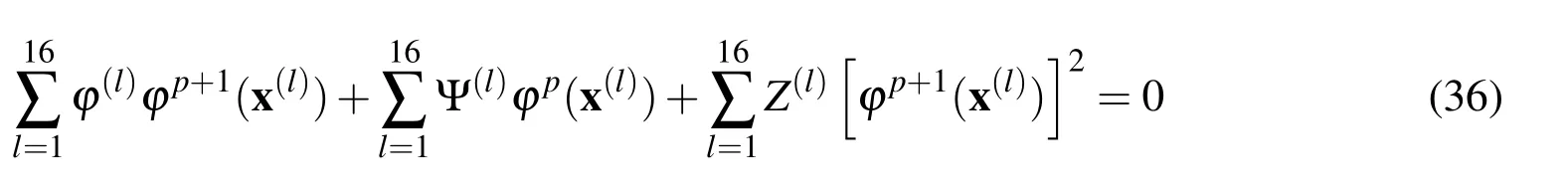
where φ(l),Ψ(l),Z(l)represent all the integrals involved in(35)and evaluated once since they are the same for all non-intersected support.

For a boundary pointx(k),the corresponding LBIE is given by equation (8) with a=Considering the discretization shown in Fig.3(b),adopting polar coordinates and following the procedure described previously,equation(8)is finally written as

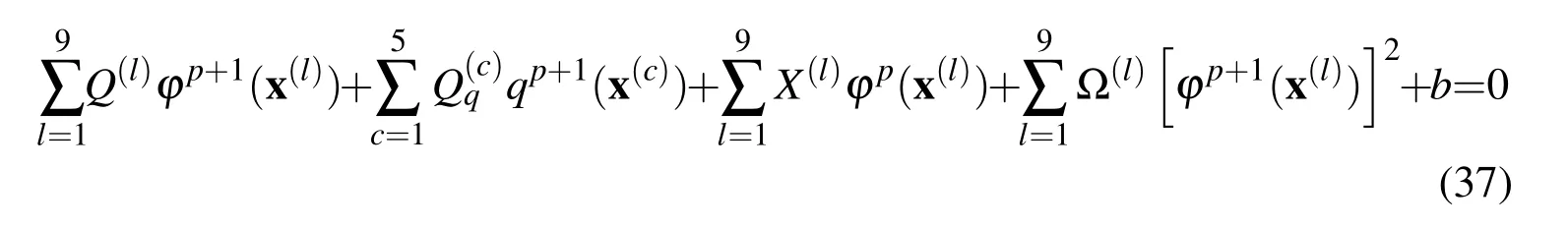
wherex(c)represents the five nodal points that define the portion of the global boundary and b is scalar coming from the application of boundary conditions.

As in(36),all the integrals defined across the circumferential direction are already known.The only integrals that have to be evaluated here are those defined across the global boundary.

The key idea of the present LBIE/LRBF method is that Eq.(36)is the same for all internal points with complete support domains and all the aforementioned“temporary”nodal fields are interpolated via the LRBF scheme illustrated in previous section.Consequently,Eqs.(36)and(37)obtain the form,respectively

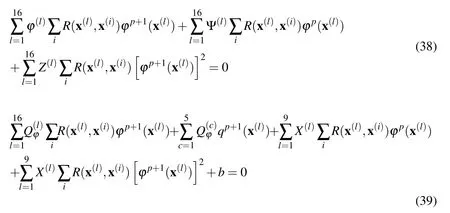
wherex(i)represents all the nodal points belonging in the support domain of each nodal or“temporary”point,shown in Fig.4 by red full circles.

Both Eqs.(38)and(39)can be written in vector form as

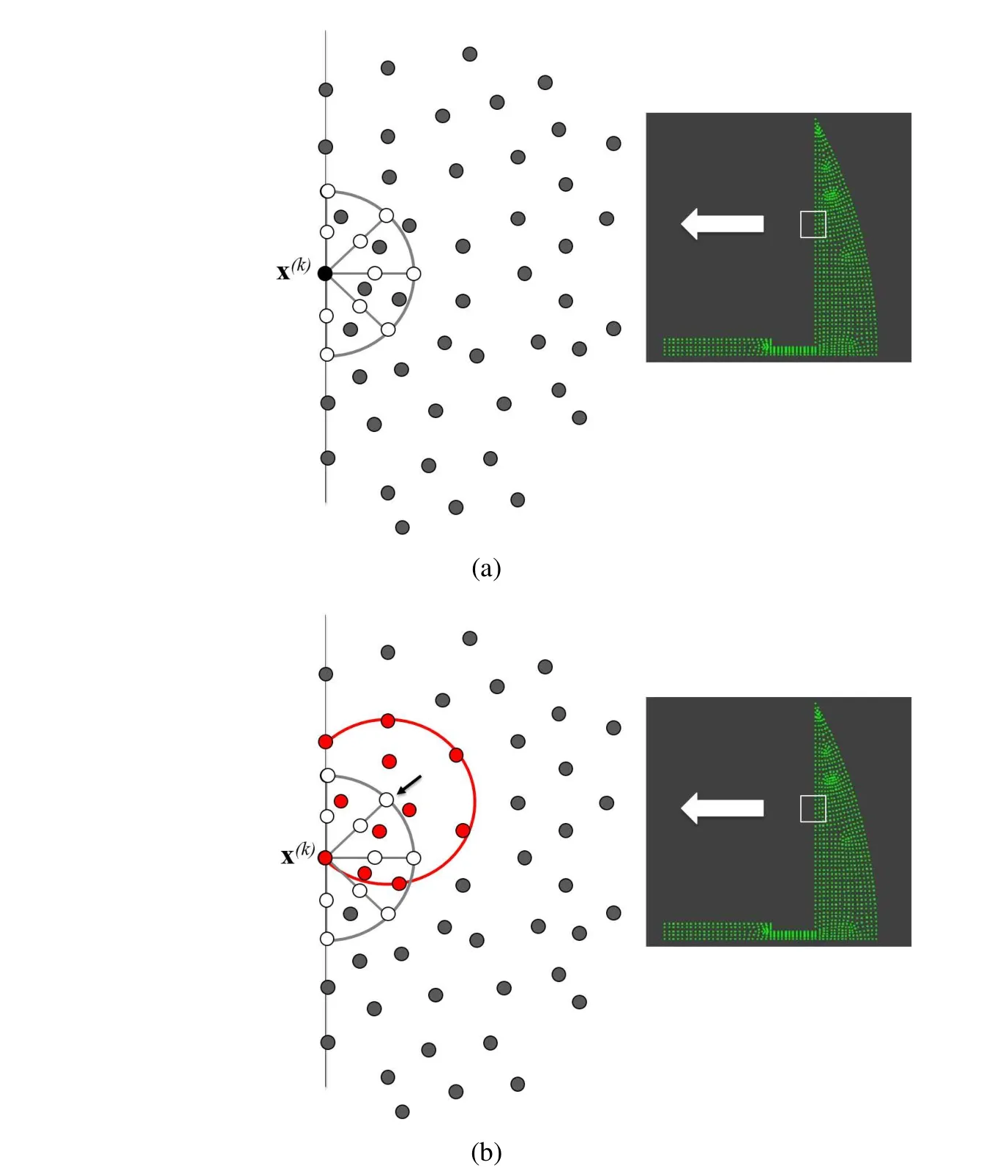
Figure 4:(a)The support domain of a boundary point x(k)intersected by the global boundary of the structure and discretized as in Figure 3.The full circles stand for the nodal points used for the meshless treatment of the structure,while the open circles represent the “temporary”nodal points.(b)The field at each “temporary”nodal point is interpolated via LRBFs defined via the nodal points(red points)belonging in the support domain(red circle)of the“temporary”nodal point indicated by the arrow.

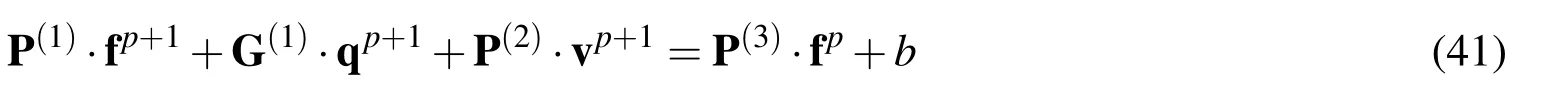
whereare vectors comprising all the unknown values of φp+1,respectively,while the vectorfpcontains all the nodal values of φpknown from the previous time step.

Collocating Eqs.(40)and(41)at all internal and boundary nodal points one obtains the following non-linear system of algebraic equations

where the vectorxcontains the unknown nodal values φp+1,qp+1and(φp+1)2and the vectorBis known from the previous time step and the boundary conditions.

The non-linear system(42)is solved according to standard Newton-Raphson algorithm adopting the following steps:

1.Make an initial guess for the unknown vectorx,letx(0).In the present work the initial guess wasx(0)=0.

2.Evaluate the Jacobian matrix∇xf(x).Since the only non-linear term is that corresponding to the nodal values(φp+1)2,it is apparent that the Jacobian is a linear matrix with respect tox.

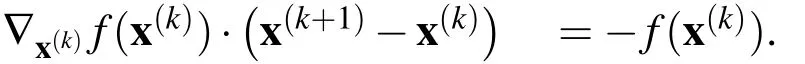
As soon as the functions φp+1and qp+1are known,the vectorcan be evaluated either by taking directly the gradient of the LRBF-interpolated φp+1or by considering the LBIE given by Eq.(10).

5 Benchmark problems

In the present section,the LBIE/BEM method illustrated in previous sections is tested with two linear benchmark problems and one nonlinear problem with a solution taken by the FEM.

Consider the 1m×1m rectangular plate shown in Fig.5(a).The upper side of the plate is subjected to a sudden thermal loading of unit temperature T=1.0 and remains at that temperature for the rest of time.The other three sides of the plate are isolated with zero temperature fluxes and all the material properties are assumed to be equal to unity.The just described transient thermal diffusion boundary value problem is represented by the following equations:

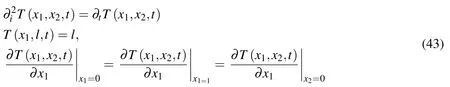
The analytical solution of(43)has the form[Carter,Beaupre,Giori and Helms(1998)]:

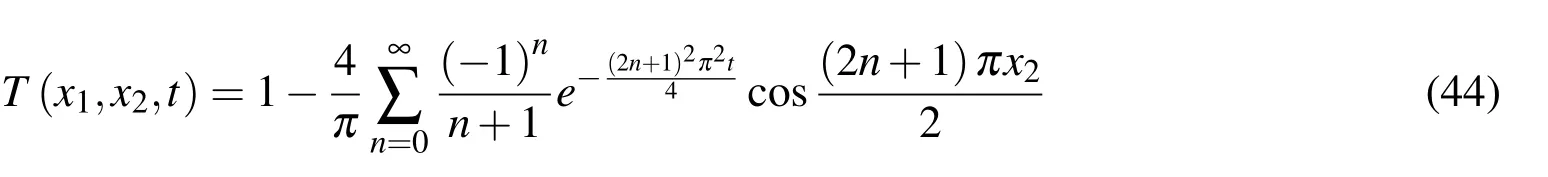
For the LBIE/LRBF solution of the problem 81 uniformly distributed internal points have been considered,while the external boundary has been discretized with 16 quadratic line elements.The support domains have been selected to be the same for all nodes and equal to 0.566 m.The temperature at(x,y)=(0.5,0.5)has been calculated and compared to analytical ones provided by Eq.(44).As it is apparent in Fig.5(b)the agreement is excellent.

The previous problem has also been solved utilizing 185 non-uniformly distributed nodal points(Fig.6a)with support domain of radius equal to 0.3456m.The temperature at(x,y)=(0.5,0.5)as a function of time has been evaluated and compared to the corresponding solution concerning uniformly distributed points in Fig.6b.The comparison shows an excellent agreement.

The accuracy of the present method in calculating the gradient of the field at any point of the analyzed domain is also tested.Concerning the above diffusion problem of the rectangular plate the analytical solution for the temperature gradient is given by

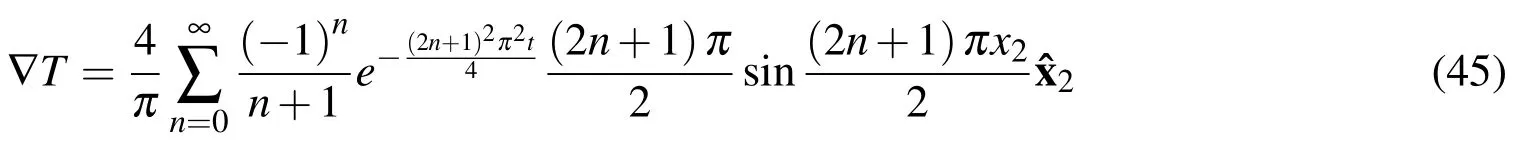
withrepresenting the unit vector at x2direction.

The gradient of the temperature at the(x,y)=(0.5,0.5)has been evaluated with the aid of the LBIE of Eq.(10)and it is compared with the analytical one provided by Eq.(45).As it is shown in Fig.7 the agreement between numerical and analytical results is excellent.

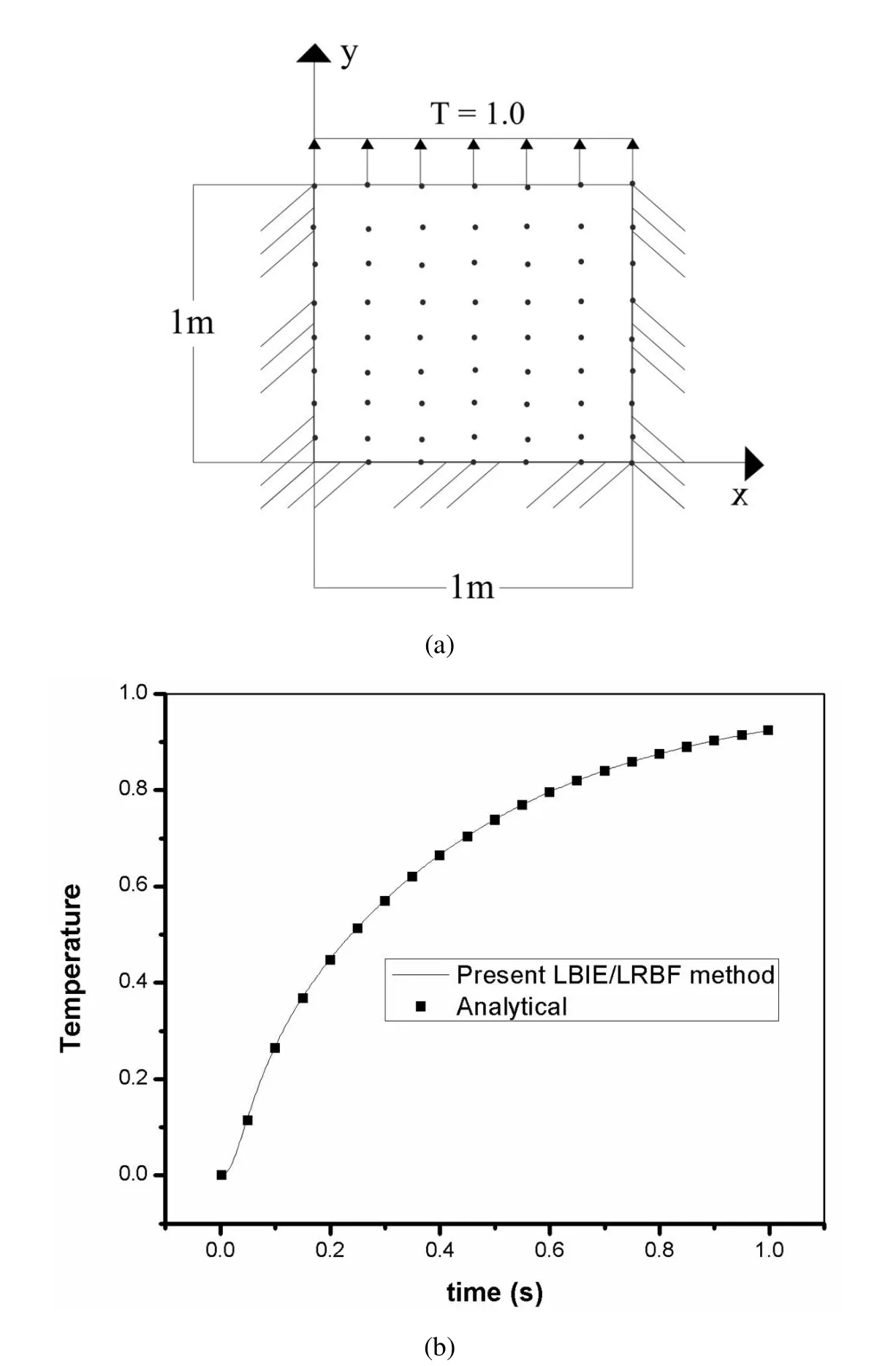
Figure 5:(a)Internal and boundary nodal points considered for the LBIE/LRBF solution of the problem described by Eq.(43).(b)Time history of temperature at(x,y)=(0.5,0.5).

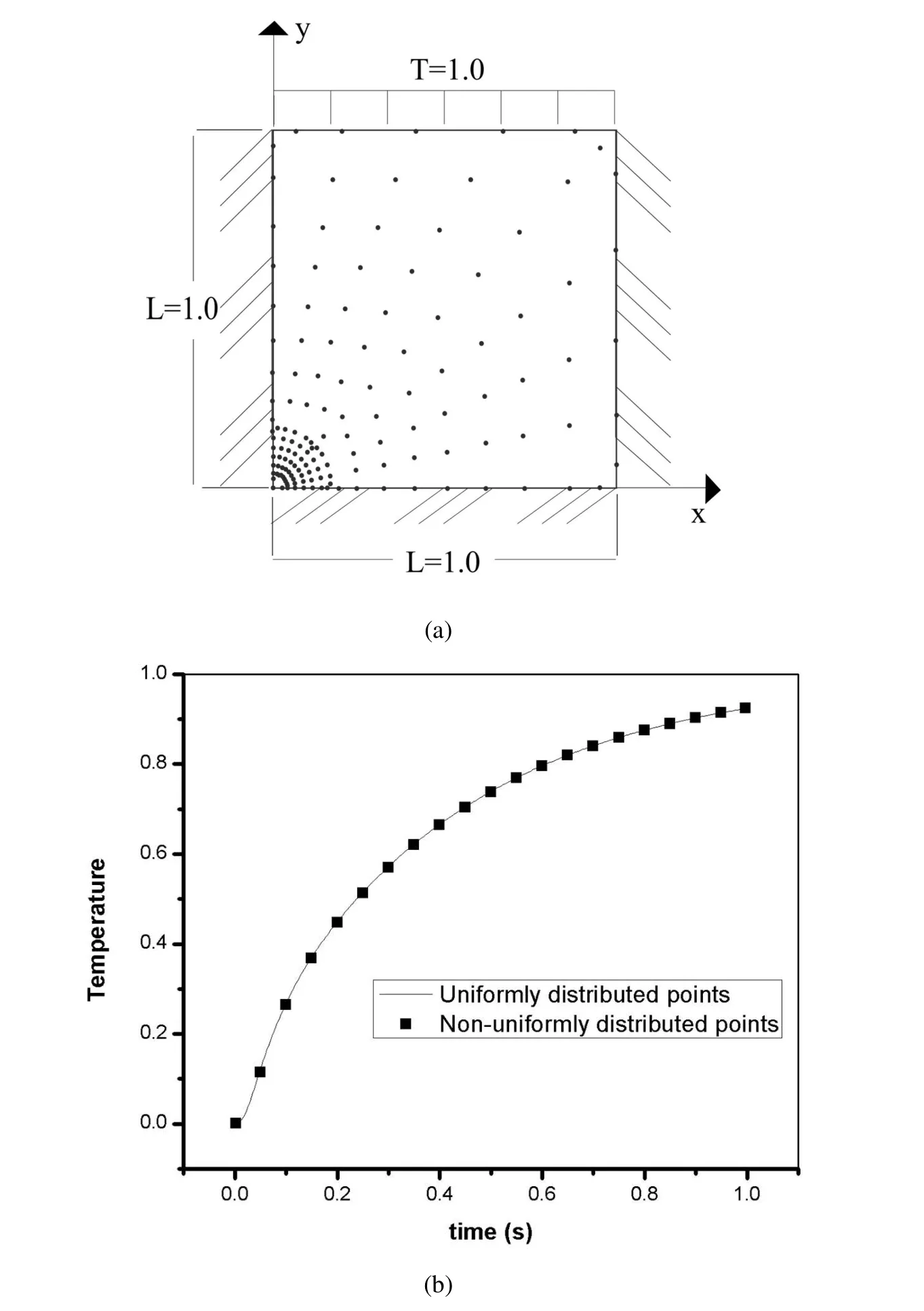
Figure 6:The problem of Fig.5 with non-unform distribution of nodal points.(a)Internal and boundary nodal points considered for the LBIE/LRBF solution of problem described by Eq.(43).(b)Time history of temperature at(x,y)=(0.5,0.5).

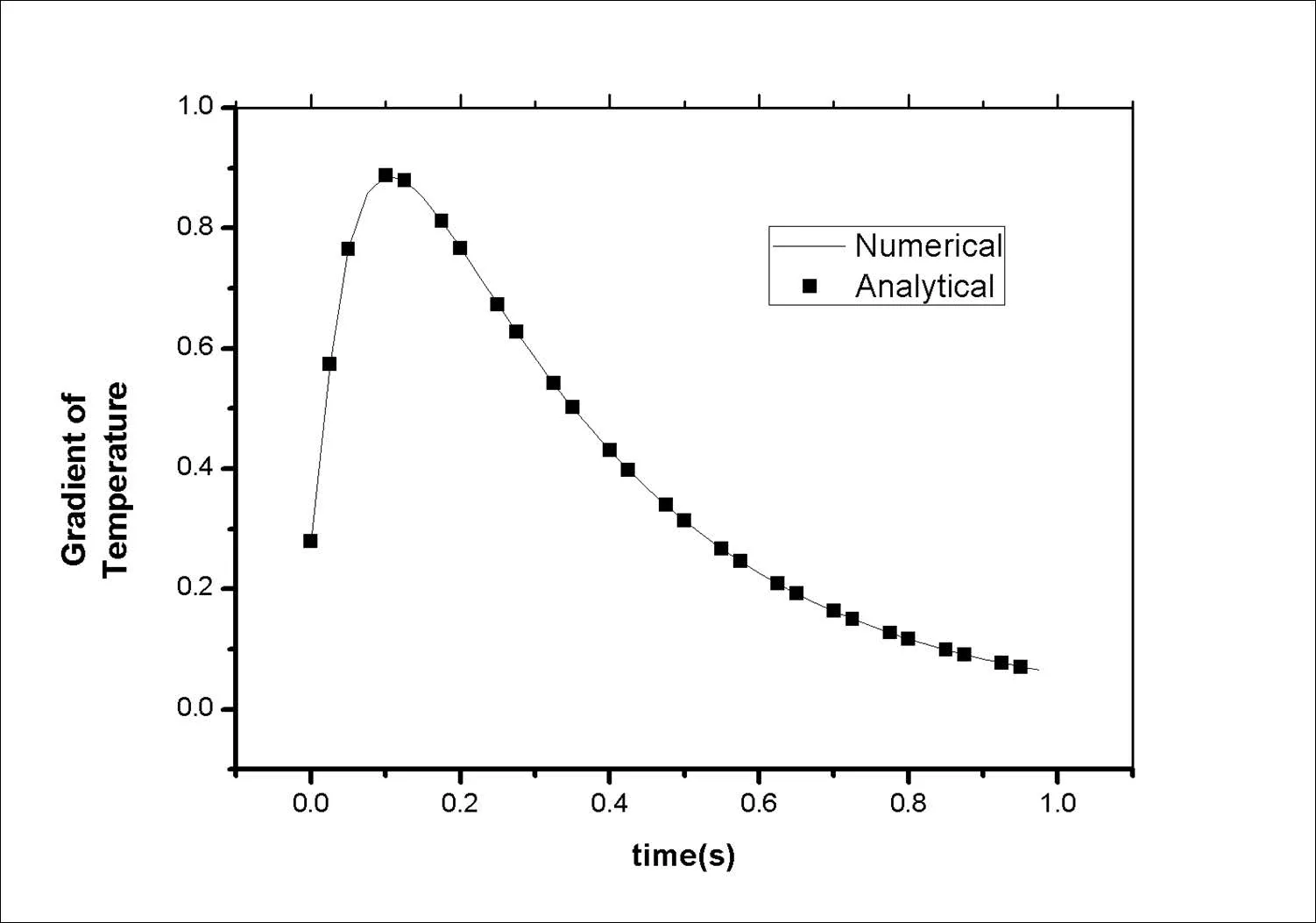
Figure 7:Time history of the gradient of temperature and comparison with the analytical solution(45).

As it has been already mentioned in section 4,the gradient of the density function φp+1can be evaluated either by using the LBIE of Eq.(10)or via the derivatives of the local radial basis interpolation functions.Comparing the accuracy provided by the two methodologies,the general conclusion is that Eq.(10)is always superior to derivatives of LRBFs especially at points lying near and on the global boundary of the considered domain.For internal points far from the external boundary the provided accuracy is comparable. For example, the numerical error appearing in the evaluation of∂iφ via the LBIE of Eq.(10)at points A(1.0,1.0),B(0.5,0.5),C(0.1,0.1)(Fig.5(a))is 0.08%,0.1%and 0.07%respectively,while via the derivatives of LRBFs at the corresponding points ∂iφ is 2.1%,1.0%and 1.8%.Knowing that the interpolation provided by the LRBFs near to the boundary points is better than that provided by their derivatives,the aforementioned behaviour is expectable since the evaluation of∂iφ through Eq(10)is accomplished by avoiding the use of derivatives of LRBFs.In that sense,the evaluation of∂iφ through the LBIE of Eq.(10)could not be characterized as“expensive”because for points lying near to the boundary provides better accuracy,while for internal points all the involved integrals in Eq.(10)are evaluated once as in the case of Eq.(9)explained in section 4.

The nonlinear version of the above mentioned problem has been solved with the coefficients D1,D2and α of Eq.(1)being D1=D2= α=1.The obtained solution is compared to the corresponding one taken through the commercial FEM package COMSOL Multiphysics 4.0a and depicted in Fig.8.As it is apparent,the agreement is very good.

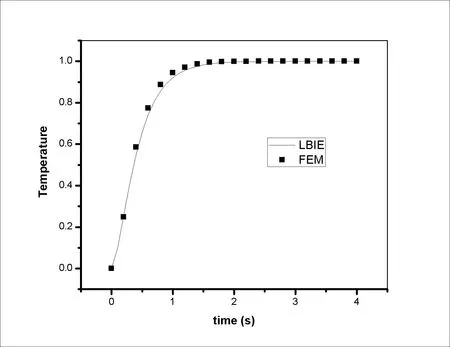
Figure 8:Temperature at(x,y)=(0.5,0.5)as a function of time for the nonlinear version of problem(43).Comparison between the results taken from COMSOL Multiphysics 4.0a and the present LBIE/LRBF.

In the sequel,the accuracy of the present LBIE/LRBF method in solving the aforementioned nonlinear problem with the non-uniformly point distribution of Fig.6 is checked.As it is shown in Fig.9 the agreement between the numerical results taken through LBIE and those taken through the commercial FEM package COMSOL Multiphysics 4.0a is excellent.

Finally,the convergence while making the mesh denser for the two cases(linear and non-linear Fisher equation)is examined.Both uniformly and non-uniformly distributed nodal points have been considered.Three mesh cases corresponding to 49,81 and 121 nodal points have been considered.Comparing to analytical and FEM solutions,the convergence error for a nodal point in the center of the rectangular plate(x,y)=(0.5,0.5)and in the upper left corner near the boundary(x,y)=(0.9,0.9),is calculated and reported in Tables 1 and 2.

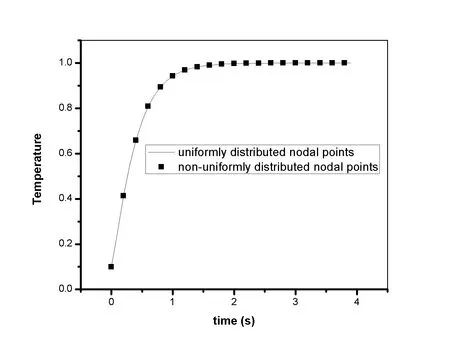
Figure 9:Temperature at(x,y)=(0.5,0.5)as a function of time for the nonlinear version of problem(43).Comparison on the obtained results when uniformly distributed points and non-uniformly distributed points are considered.

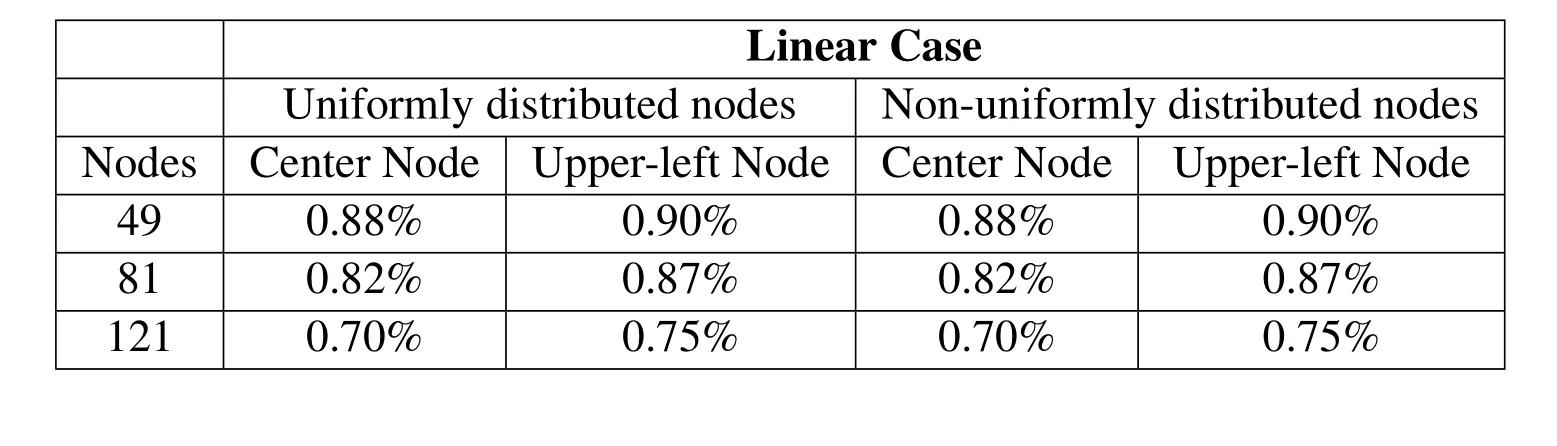
Table 1:Mesh convergence error for the linear case(uniformly and non-uniformly distributed nodes.Center and upper left node checked).

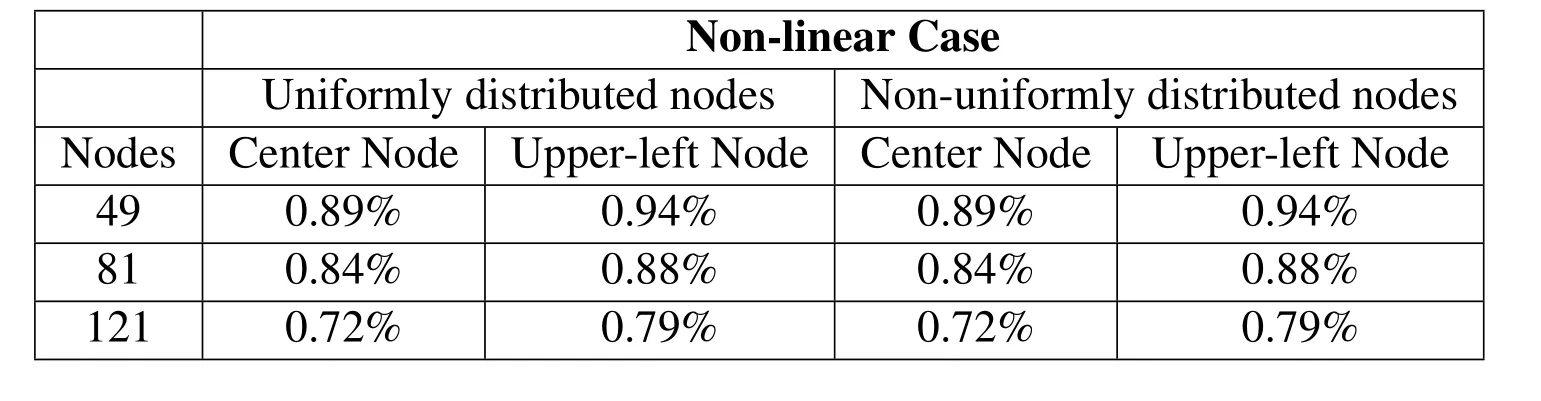
Table 2:Mesh convergence error for the non-linear case(uniformly and nonuniformly distributed nodes.Center and upper left node checked).

6 Application to bone healing

The process of bone fracture healing includes complex sequence of cellular events which gradually restore the functional and mechanical bone properties,such as load-bearing capacity,stiffness and strength.Initially an inflammatory reaction takes place and a hematoma is formed at the fracture gap forming an initial fracture callus that mainly consists of mesenchymal cells.Then along the bone mesenchymal cells differentiate into osteoblasts which begin to synthesize bone.In the interior of the initial callus and adjacent to the fracture mesenchymal cells differentiate into chondrocytes which synthesize cartilage.Subsequently blood vessels are formed in the calcified cartilage which is then absorbed by osteoclasts.The cartilage is replaced with ossified tissue and woven bone is formed via endochondral ossification of the callus.Finally the remodelling stage takes place in which the external callus is completely resorbed and in the fracture gap the disorganized osteoclasts and osteoblasts are remodeled into cortical.

The determination of the underlying cellular mechanisms of bone healing remains an open issue in the literature,despite the intensive work that has been conducted in the field.To this end several mechanobiological computational models have been proposed aiming to investigate and derive quantitative criteria that describe how mechanical stimulation affects tissue differentiation,growth,adaptation and maintenance during bone healing[Gao(2002,2005);Carter,Beaupre,Giori and Helms(1998);Claes and Heigele(1998);Prendergast(1997);Lacroix and Prendergast(2002)].

Most of the existing mechanobiology models incorporate bioregulatory models which simulate the cellular processes such as dispersion and proliferation in biologic tissues via diffusion equations [Andreykiv, Van Keuler and Prendergast (2008);Claes and Heigele(1998);Prendergast(1997)]. [Lacroix and Prendergast(2002)]were the first to account for cell phenomena such as cell migration,proliferation and differentiation with the aid of diffusion equations.In this model progenitor cells were assumed to originate from different parts of healing bone i.e.,periosteum and bone marrow.[Bailon-Plaza and van der Meulen(2001)]also modeled migration and proliferation of mesenchymal cells as well as chondrocyte and osteoblast proliferation and differentiation via diffusive processes.In another study[Isaksson,Donkelaar,Huiskes and Ito(2008)]the cellular processes are directly connected with mechanical stimulation and act at cell-phenotype rates.

In all of the aforementioned studies numerical predictions of tissue differentiation and bone healing are derived using the Finite Element Method.Although FEM is a well-known and robust numerical method,when applied to problems dealing with phase changes,suffers from global remeshing when new born surfaces or material phases appear.On the other hand in meshless methods no background cells are required for the numerical evaluation of the involved integrals[Sellountos and Sequeira(2008b);Wang and Liu(2002)].This renders the present LBIE/LRBF method ideal for solving problems with moving or new-born boundaries since it avoids remeshing as new bone solidification regions appear.

In this subsection the LBIE/LRBF method is used for the first time for deriving predictions of cell distribution in fractured bone during the healing process.

Although in most cases the description of cell activities is achieved by complicated systems of partial differential equations that correlate all the types of cells involved in bone healing process,we adopt herein a simplified but rather effective model in which the concentration of all cell types is modeled as one parameter following the Fisher Eq.(1).

6.1 Geometrical model of healing bone

We considered a 2D model of callus based on previous mechanical models of healing bone[Isaksson,Donkelaar,Huiskes and Ito(2008)]as shown in Fig.10.The cortical bone had inner and outer diameters of 14 mm and 20 mm [Isaksson, Donkelaar,Huiskes and Ito(2008);Claes and Heigele(1998)].

Cells were assumed to distribute according to Eq.(1)in which the field c(x1,x2,t)is the cell concentration within the callus region.Solution was derived for a=1 i.e.,a non-linear diffusion equation.Cell parameters were considered equal to those of mesenchymal stem cells(MSC)[Isaksson,Donkelaar,Huiskes and Ito(2008)].The diffusivity was equal to 0.65mm2/day[Isaksson,Donkelaar,Huiskes and Ito(2008)]. Initially fixed MSC concentrations were assumed at the periosteum,the marrow interface and the interface between bone and callus at the fracture site as depicted in Fig.10.In addition,across the remainder external boundaries zero flux was assumed(Fig.10(b))i.e.,

Numerical calculations were performed for 100 iterations which correspond to 40 days post-fracture.The interior of the callus is fulfilled with 642 distributed nodes(Fig.10c)with support domains of radius 0.4256.

6.2 Numerical Predictions of cell distribution during bone healing

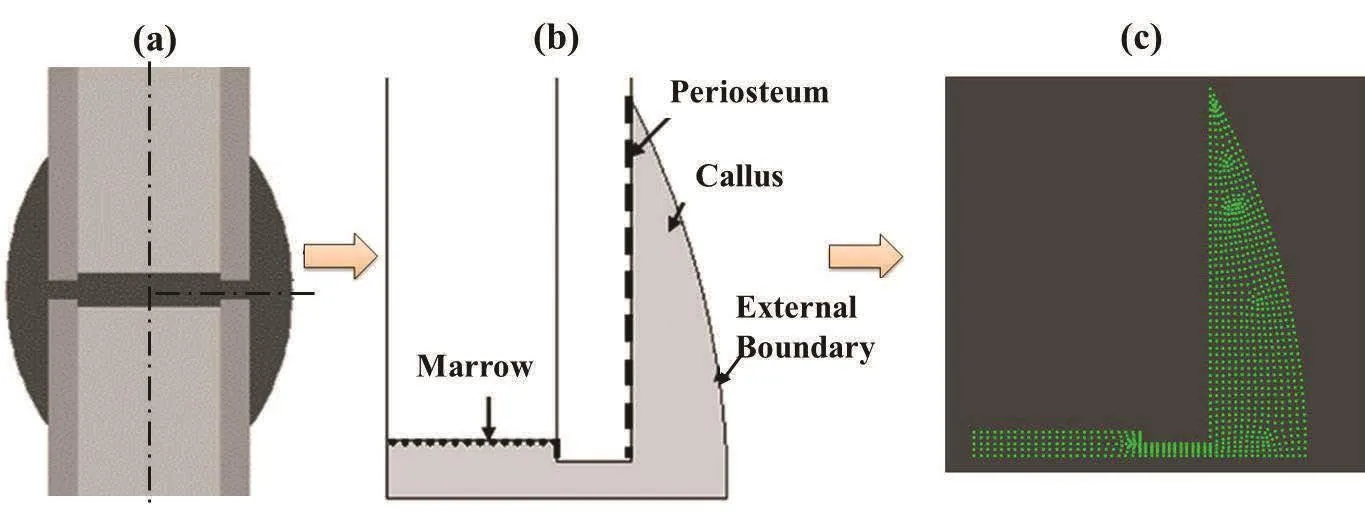
Figure 10:(a)Two-Dimensional model of healing bone,(b)callus model,[2](c)callus geometry discretized by randomly distributed points.

The MSC distribution in the callus area during the process of bone healing is shown in Fig 11.The red colors correspond to maximum cell concentrations whereas blue ones to minimum.As shown in Figs.11(a),(b)MSCs initially(i.e.,at the beginning and day 1)proliferate along the periosteum covering first the remote fracture site.Augmented cell concentrations are also observed at the regions along the periosteum at some distance from the gap.As the days pass,MSC proliferation rapidly evolves along periosteum and fracture gap(Fig.11(c)).Concurrently cell concentrations are significantly increased in the fracture gap after day 6,which suggests that progressive intramembraneous ossification occurs possibly followed by endochondral replacement.Finally at day 8 MSC distribution is shown to decrease along the periosteum(Fig.11(d)).After that day there are no more changes in MSC concentrations and thus a plateau is reached.

From the results it is clear that the proposed LBIE method is able to predict several physiological aspects of bone healing.MSC activity at the fracture gap started from the 5th day and was rapidly increasing.Therefore MSCs differentiate into fibroblasts leading to the formation of fibrous tissue close to the fracture ends.Concurrently at 8th day cells started proliferate along the periosteum at a distance from the fracture gap,which may be indicative of an initial intramembraneous bone formation.Cell proliferation was also found to successively increase at the regions closer to the fracture gap possibly towards the development of cartilage.

Numerical solution has been also derived for the corresponding linear diffusion problem i.e.,assuming a=0 in Eq.1,for comparison purposes.The derived MSC distributions in the callus region during the 1st,3rdand 8thday post-fracture are shown in Fig.12(a),(b)and(c)respectively.

At day 1 MSC proliferation starts along the periosteum at a distance from the fracture site.As the days pass proliferation continues the gap as well(Figs.12(b)and(c)).The phenomenon evolves until the 8thwhich is in accordance with the nonlinear case.However,the linear diffusion model predicts that proliferation stops at a distance from the external callus booundary and the most intensive cell action is observed along the periosteun at a remote fracture site.On the other hand,in the non-linear model the most increased cell activity is observed within the whole callus region,which suggests that non-linear diffusion models can provide more realistic decription of biological healing processes such as MSC proliferation.

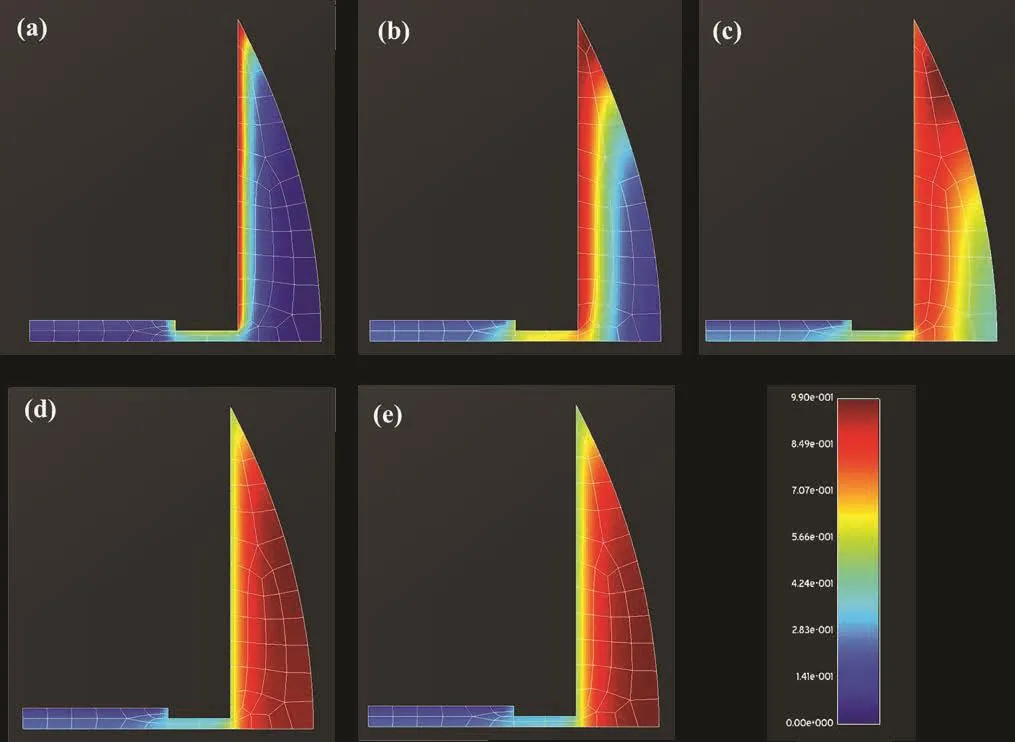
Figure 11:Predicted distributions of MSC in the callus during normal fracture healing at(a)day 0(beginning of the phenomenon),(b)day 1,(c)day 2,(d)day 5 and(e)day 8.

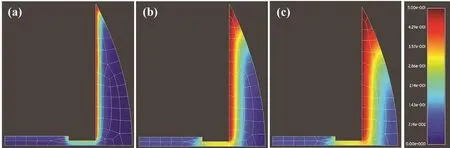
Figure 12:MSC distributions in the callus during normal fracture healing at(a)day 1,(b)day 3 and(c)day 8 derived from the linear diffusion equation.

Our findings make clear that meshless LBIE method seems promising in describing complicated biological mechanisms that occur during bone healing.Therefore enhanced bioregulatory models based on such computational methods could be proved effective for the quantitative evaluation of bone pahtologies.

7 Discussion-Conclusion

In this work a simple meshless LBIE/LRBF methodology for solving the 2D Fisher non-linear transient diffusion equation has been reported.The method utilizes a cloud of randomly distributed and without any connectivity requirements points covering the domain of interest and a BEM mesh for the representation of the external boundary.At each point a circular support domain is centered and a LBIE is assigned.The Laplace fundamental solution is employed and thus,each LBIE contains surface integrals defined at the circular boundary of the support domain and volume integrals coming from the non-Laplacian terms of Fisher equation.For intersected support domains by the global boundary,the corresponding LBIE comprizes both integrals defined at the circular boundary of the support domain and integrals defined at the portion of the global boundary intersected by the support domain of the considered point.A finite difference scheme is utilized for the time derivative of Fisher equation.In all the considered LBIEs, fluxes defined at the circular boundaries are eliminated with the aid of companion solutions derived in the framework of the present work.The accuracy of the addressed LBIE/LRBF method remains high as that provided by previous LBIE formulations proposed by Sellountos,Polyzos and collaborators.As far as the efficiency of the method is concerned,the obvious improvement is the much faster formation of the final algebraic equations for all the internal points the support domain of which do not intersect the global boundary.Because of that,the efficiency of the proposed LBIE/LRBF method is obviously better than that of our previous LBIE formulations and the formation of the algebraic equations of each internal point is at least ten times faster in the present LBIE/LRBF formulation.That advantage becomes more pronounced when uniform distributions of points are considered.

The novelty of the present meshless LBIE/LRBF formulation for solving nonlinear transient diffusion problems can be summarized as follows:(i)Utilizing the idea proposed by[Popov and Bui(2010)]and[Sellountos, Polyzos and Atluri(2012)]and illustrated in section 4, all the points with non-intersected support domains have the same LBIE given by Eq.(36).Thus,all the involved integrals are evaluated once and the final system of algebraic equations is formed quickly and economically.Making use of companion solutions derived in the present work,the proposed formulation is different than that of[Popov and Bui(2010)]since it employs,for each point,only the regular LBIE and not the regular plus the hypersingular LBIE as the Popov-Bui methodology does.(ii)The volume integrals are implemented with the aid of the integration technique proposed by[Gao(2002,2005)],which transforms all the volume integrals to line ones avoiding thus time consuming domain descritization techniques or the DR-BEM for converting the volume integrals to surface ones.(iii)The stability of the proposed LBIE/LRBF is excellent even for irregular distribution of nodal points.(iv)The convergence of the method is accomplished with relatively coarse distribution of points and the final accuracy is less than 0.1%even for boundary and near to the boundary points.(v)The gradient of density function at any point of the analyzed domain is evaluated after the solution of the final system of algebraic equations and employing the hypersigular LBIE of the considered point instead of the derivatives of RBFs.The higher accuracy of that technique is con firmed in the benchmark problems and it is in accordance with the well known advantage of BEM over FEM when the BEM utilizes the hypersingular integral equation and the FEM derivatives of shape functions for the evaluation of gradients of density functions at or near to the global boundary.Thereafter the method was applied for investigating MSC proliferation and calculate cell concentration during bone healing.Numerical simulations were performed in a 2D model of callus.MSCs were assumed to distribute according to the Fisher equation and originate from the bone-callus interface,the bone marrow and the periosteum.Predictions were performed for a linear and a non-linear diffusion case.Although in both cases cell proliferation was completed within the same time(i.e.,at the 8thday)the non-linear model provided more realistic results since MSCs were predicted to progressively proliferate within the whole callus region rather than along the periosteum(which was found in the linear model).Overall,meshless LBIE method can capture significant events that occur during bone healing such as intramembraneous bone formation starting far from the fracture gap.Furthermore,it can be combined effectively with a corresponding technique for solving poroelastic problems and thus to provide effective solutions in bone healing processes,where new phases appear,without the need of rediscretization of the analyzed domain.

Acknowledgement:The research project is implemented within the framework of the Action “Supporting Postdoctoral Researchers”of the Operational Program"Education and Lifelong Learning"(Action’s Beneficiary:General Secretariat for Research and Technology),and is co- financed by the European Social Fund(ESF)and the Greek State(PE8-3347)

Andreykiv,A.;Van Keulen,F.;Prendergast,P.J.(2008):Simulation of fracture healing incorporating mechanoregulation of tissue differentiation and dispersal/proliferation of cells.Biomech.Model.Mechanobiol.,vol.7,no.6,pp.443-461.

Atluri,S.N.(2004):The meshless method(MLPG)for domain&BIE discretizations.Tech Science Press.

Atluri,S.N.;Shen,S.(2002):The Meshless Local Petrov-Galerkin(MLPG)Method.Tech.Science Press.

Atluri,S.N.;Zhu,T.(1998):A new meshless local Petrov-Galerkin(MLPG)approach to nonlinear problems in computer modeling and simulation.Comput.Model.Simul.Eng.,vol.3 pp.187-196.

Bailon-Plaza,A.;Van der Meulen,M.C.(2001):A mathematical framework to study the effects of growth factor influences on fracture healing.J.Theor.Biol.,vol.212,pp.191-209.

Bourantas,G.C.;Burganos,V.N.(2013):An implicit meshless scheme for the solution of transient non-linear Poisson-type equations.Eng.Anal.Bound.Elem.,vol.37,pp.1117-1126.

Bourantas,G.C.;Skouras,E.D.;Loukopoulos,V.C.;Nikiforidis,G.C.(2010):Numerical solution of non-isothermal fluid flows using Local Radial Basis Functions(LRBF)interpolation and a velocity-correction method.CMES:Comp Mod Eng&Sci.,vol.64,no.2,pp.187-212.

Buhmann,M.D.(2004):Radial Basis Functions:Theory and Implementations.Cambridge University Press.

Carter,D.R.;Beaupre,G.S.;Giori,N.J.;Helms,J.A.(1998):Mechanobiology of skeletal regeneration,Clin.Orthop.355S S41-S55.

Chen,L.;Liew,K.M.(2011):A local Petrov-Galerkin approach with moving Kriging interpolation for solving transient heat conduction problems.Comp.Mech.,vol.47,no.4,pp.455-467.

Claes,L.E.;Heigele,C.A.(1998):Magnitudes of local stress and strain along bony surfaces predict the course and type of fracture healing.J.Biomech.,vol.32,pp.255-266.

Fisher,R.A.(1937):The wave of advantageous genes.Ann.Eugenics.,vol.7,pp.353-369.

Gao,X-W.(2002):The radial integration method for evaluation of domain integrals with boundary-only discretization.Engin.Anal.Bound.Elem.,vol.26,pp.905-916.

Gao,X-W.(2005):Evaluation of regular and singular domain integrals with boundaryonly discretization-theory and Fortran code.Journ.Comp.App.Math.,vol.175,pp.265-290.

Garcia-Aznar,J.M.;Kuiper,J.H.;Gomez-Benito,M.J.;Doblare,M.;Richardson,J.B.(2007):Computational simulation of fracture healing:influence of interfragmentary movement on the callus growth.Journ.Biomech.,pp.1467-1476.

Gilhooley,D.F.;Xiao,J.R.;Batra,M.A.;McCarthy,M.A.;Gillespie,J.

W.J.(2008):Two dimensional stress analysis of functional graded solids using the MLPG method with radial basis functions.Comp.Mat.Scien.,vol.41,pp.467-481.

Gunzburger,M.D.;Hou,L.S.;Zhu,W.(2005):Modeling and analysis of the forced Fisher equation.Nonlin.Anal.,vol.62,pp.19-40.

Guo,L.;Chen,T.;Gao,X.W.(2012):Transient meshless boundary element method for prediction of chloride diffusion in concrete with time dependent nonlinear coefficients.Engin.Anal.Bound.Elem.,vol.36 pp.104-111.

Hardy,R.(1990):Theory and applications of the multiquadrics-biharmonic method(20 years of discovery 1968-1988).Comput.Math.Appl.,vol.19,pp.163-208.

Isaksson,H.;Van Donkelaar,C.C.;Huiskes,R.;Ito,K.(2008):A mechanoregulatory bone-healing model incorporating cell-phenotype specific activity.Journ.Theor.Biol.,vol.252,pp.230-246.

Katsikadelis,J.T.;Nerantzaki,M.S.(1999):The boundary element method for nonlinear problems.Eng Anal.Bound.Elem.,vol.23,no.5-6,pp.365-373.

Khiari,N.;Omrani,K.(2011):Finite difference discretization of the extended Fisher-Kolmogorov equation in two dimensions.Comp.and Mathem.Appl.,vol.62,pp.4151-4160.

Lacroix,D.;Prendergast,P.J.(2002):A mechano-regulation model for tissue differentiation during fracture healing:analysis of gap size and loading.J.Biomech.,vol.35,pp.1163-1171.

Lin,H.;Atluri,S.N.(2000):Meshless Local Petrov-Galerkin(MLPG)Method for Convection-Diffusion Problems.CMES:Comp.Mod.Eng.Sci.,vol.1,no.2,pp.45-60.

Li,S.;Liu,W.K.(2007):Meshfree Particle Methods.Springer Verlag Berlin Heidelberg,New York.

Mirzaei,D.;Dehghan,M.(2011):MLPG method for transient heat conduction problem with mls as trial approximation in both time and space domains.CMES:Comp.Model.Engin.Sci.,vol.72,no.3,pp.185-210.

Mohammadi,M.;Hematiyan,M.R.;Marin,L.(2010):Boundary element analysis of nonlinear transient heat conduction problems involving non-homogenous and nonlinear heat sources using time-dependent fundamental solutions.Eng Anal.Bound.Elem.,vol.34,pp.655-665.

Moreo,P.;Gaffney,E.A.;Garcia-Aznar,J.M.;Doblare M.(2010):On the modeling of biological patterns with mechanochemical models:insights from analysis and computations.Bullet.Mathem.Biol.,vol.72,pp.400-431.

Petrovskii,S.;Shigesada,N.(2001):Some exact solutions of a generalized Fisher equation related to the problem of biological invasion.Mathem.Biosc.,vol.172,pp.73-94.

Popov,V.;Bui,T.T.(2010):A meshless solution to two-dimensional convection diffusion problems.Eng.Anal.Bound.Elem., vol.34,pp.680-689.

Prendergast,P.J.(1997):Finite element models in tissue mechanics and orthopaedic implants design.Clin.Biomech.,vol.12,pp.343-366.

Prokharau,P.A.;Vermolen,F.J.;García-Aznar,J.M.(2013):Numerical method for the bone regeneration model,de fined within the evolving 2D axisymmetric physical domain.Comput.Meth.Appl.Mech.Eng.,vol.253,pp.117-145.

Sarler,B.;Vertnik,R.(2006):Meshfree explicit local radial basis function collocation method for diffusion problems.Comp.Math.and Appl.,vol.51,pp.1269-1282.

Sellountos,E.J.;Polyzos,D.;Atluri,S.N.(2012):A New and Simple Meshless LBIE-RBF Numerical Scheme in Linear Elasticity.CMES:Comp.Model.Eng Sci.,vol.89,no.6,pp.513-551.

Sellountos,E.J.;Sequeira,A.(2008a):An advanced meshless LBIE/RBF method for solving two-dimensional incompressible fluid flows.Comp Mech.,vol.41,pp.617-631.

Sellountos,E.J.;Sequeira,A.(2008b):A Hybrid Multi-Region BEM/LBIERBF Velocity-Vorticity Scheme for the Two-Dimensional Navier-Stokes Equations.CMES:Comp.Model.Eng.Sci.,vol.23,no.2,pp.127-147.

Sellountos,E.J.;Sequeira,A.;Polyzos,D.(2009):Elastic transient analysis with MLPG(LBIE)method and local RBFs.CMES:Comp.Model.Eng Sci.,vol.41,no.3,pp.215-242.

Sellountos,E.J.;Sequeira,A.;Polyzos,D.(2010):Solving Elastic Problems with Local Boundary Integral Equations(LBIE)and Radial Basis Functions(RBF)Cells.CMES:Comp Model Eng Sci.,vol.57,no.2,pp.109-135.

Sengers,G.;Please,C.P.;Oreffo,R.O.C.(2007):Experimental characterization and computational modeling of two-dimensional cell spreading for skeletal regeneration.J.R.Soc Interface,vol.4,pp.1107-1117.

Shirzadi,A.;Sladek,V.;Sladek,J.(2013):A local integral equation formulation to solve coupled nonlinear reaction-diffusion equations by using moving least square approximation.Engin.Anal.Bound.Elem.,vol.37,pp.8-14.

Shivanian,E.(2013):Analysis of meshless local radial point interpolation(MLRPI)on a nonlinear partial integro-differential equation arising in population dynamics.Engin.Anal.Bound.Elem.,vol.37,pp.1693-1702.

Sladek,J.;Sladek,V.;Tan,C.L.;Atluri,S.N.(2008):Analysis of Heat Conduction in 3D Anisotropic Functionally Graded Solids,by the MLPG.CMES:Comp.Model.Engin.Sci.,vol.32,no.3,pp.161-174.

Sladek,J.;Sladek,V.;Zhang,Ch.(2004):A local BIEM for analysis of transient heat conduction with nonlinear source terms in FGMs.Engin.Anal.Bound.Elem.vol.28,pp.1-11.

Sladek,J.;Stanak,P.;Han,J.D.;Sladek,V.;Atluri,S.N.(2013):Applications of the MLPG Method in Engineering&Sciences:A Review.CMES:Comp.Model.Engin.&Sci.,vol.92,no.5,pp.423-475.

Trobec,R.;Kosec,G.;Sterk,M.;Sarler,B.(2012):Comparison of loacal weak and strong form meshless for 2-D diffusion equation.Engin.Anal.Bound.Elem.,vol.36,pp.310-321.

Wang,J.;Liu,G.(2002):A point interpolation meshless method based on radial basis functions.Intern.Journ.Num.Meth.Eng.,vol.54,pp.1623-1648.

Wang,J.;Liu,G.(2002):On the optimal shape parameters of radial basis functions used for 2-D meshless methods.Comp.Meth.Appl.Mech.Eng.,vol.191,no.23-24,pp.2611-2630.

Zhu,T.;Zhang,J.D.;Atluri,S.N.(1998):A local boundary integral equation(LBIE)method in computational mechanics and a meshless discretization approach.Comput.Mech.,vol.21,pp.223-235.

Zhu,T.;Zhang,J.D.;Atluri,S.N.(1999):A Meshless Numerical Method Based on The Local Boundary Integral Equation(LBIE)to Solve Linear and Nonlinear Boundary Value Problems.Eng.Anal.Bound.Elem.,vol.23,pp.375-389.