A Semi-analytical Method for Vibrational and Buckling Analysis of Functionally Graded Nanobeams Considering the Physical Neutral Axis Position

1 Introduction

Functionally graded materials(FGMs)are composite materials with inhomogeneous micromechanical structure and are generally composed of two different parts such as ceramic and metal in which the material properties changes smoothly between two surfaces.This kind of material as a novel generation of composites of microscopical heterogeneity are achieved by controlling the volume fractions,microstructure,porosity,etc.of the material constituents during manufacturing,resulting in spatial gradient of macroscopic material properties of mechanical strength and thermal conductivity[Ebrahimi&Rastgoo(2008a,b)].As a result,in comparison with traditional composites,FGMs possess various advantages,for instance,ensuring smooth transition of stress distributions,minimization or elimination of stress concentration,and increased bonding strength along the interface of two dissimilar materials.Therefore,FGMs have received wide applications in modern industries including aerospace,mechanical,electronics,optics,chemical,biomedical,nuclear and civil engineering to name a few during the past two decades.Motivated by these engineering applications,FGMs have also attracted intensive research interests,which were mainly focused on their static,dynamic and vibration characteristics of FG structures[Ebrahimi et al.(2009a,b)].

Recently there has been growing interest for application of nonlocal continuum mechanics especially in the field of fracture mechanics,dislocation mechanics and micro/nano technologies.Structural elements such as beams,plates,and membranes in micro or nanolength scale are commonly used as components in micro/nano electromechanical systems(MEMS/NEMS).Therefore understanding the mechanical and physical properties of nanostructures is necessary for its practical applications.At nanolength scales,size effects often become prominent,which cause an increasing interest in the general area of nanotechnology.The classical continuum mechanics is unable to account for the size effects.Therefore,we need to consider the small length scales associated with nanostructures such as lattice spacing between individual atoms,surface properties,grain size,etc.Nonlocal elasticity theory introduced by Eringen accounts for the small-scale effects arising at the nanoscale level.It has been extensively applied to analyze the bending,buckling,vibration and wave propagation of beam-like elements in nanomechanical devices.Unlike the constitutive equation in classical elasticity,Eringen’s nonlocal elasticity theory states that the stress at a point in a body depends not only on the strain at that point,but also on those at all points of the body.This observation is in accordance with atomic theory of the lattice dynamics and experimental observation of the phonon dispersion.

Nanoscale engineering materials have significant mechanical,electrical and thermal performances that are superior to the conventional structural materials.They have attracted great interest in modern science and technology after the invention of carbon nanotubes(CNTs)by Iijima(1991).For example,in micro/nano electromechanical systems;nanostructures have been used in many areas including communications,machinery,information technology and biotechnology technologies.In recent years,nanobeams and CNTs hold a wide variety of potential applications[Zhang et al.(2004);Wang(2005);Wang and Varadan(2006)]such as sensors,actuators,transistors,probes,and resonators in NEMSs.So far,three main methods were provided to study the mechanical behaviors of nanostructures:atomistic model[Baughman et al.(2002)],semi-continuum and continuum models[Wang and Cai(2006)].However,both atomistic and semi-continuum models are computationally expensive and are not suitable for analyzing large scale systems.In other words,since conducting experiments at the nanoscale is a daunting task,and atomistic modeling is restricted to small-scale systems owing to computer resource limitations,continuum mechanics offers an easy and useful tool for the analysis of CNTs.Therefore,there are considerable efforts made to develop and calibrate continuum structural models for CNTs analysis.Moreover due to the inherent size effects,at nanoscale,the mechanical characteristics of nanostructures are often significantly different from their behavior at macroscopic scale.Such effects are essential for nanoscale materials or structures and the influence on nanoinstruments is great[Maranganti and Sharma(2007)].Consequently,the classical continuum models need to be extended to consider the nanoscale effects and this can be achieved through the nonlocal elasticity theory proposed by Eringen[Eringen and Edelen(1972)]which considers the size-dependent effect.According to this theory,the stress state at a reference point is considered as a function of strain states of all points in the body.This nonlocal theory is proved to be in accordance with atomic model of lattice dynamics and with experimental observations on phonon dispersion[Eringen(1983)].In nonlocal theory,the nonlocal nanoscale in the constitutive equation could be considered simply as a material-dependent parameter.The ratio of internal characteristic scale(such as lattice parameter,C-C bond length,granular distance,etc.)to external characteristic scale(such as crack length,wave length,etc.)is defined within a nonlocal nanoscale parameter.If the internal characteristic scale is much smaller than the external characteristic scale,the nonlocal nanoscale parameter approaches zero and the classical continuum theory is recovered.

The application of nonlocal elasticity theory,in micro and nanomaterials has received a considerable attention within the nanotechnology community.Peddieson et al.(2003)proposed a version of nonlocal elasticity theory which is employed to develop a nonlocal Euler-Bernoulli beam model.Wang and Liew(2007)carried out the static analysis of micro-and nano-structures based on nonlocal continuum mechanics using Euler-Bernoulli beam theory and Timoshenko beam theory.Aydogdu(2009)proposed a generalized nonlocal beam theory to study bending,buckling,and free vibration of nanobeams based on Eringen model and using different beam theories.Phadikar and Pradhan(2010)reported finite element formulations for nonlocal elastic Euler-Bernoulli beam and Kirchoff plate theory.Pradhan and Murmu(2010)investigated the flapwise bending-vibration characteristics of a rotating nanocantilever by using differential quadrature method(DQM).They noticed that small-scale effects play a significant role in the vibration response of a rotating nanocantilever.Civalek et al.(2010)presented a formulation of the equations of motion and bending of Euler-Bernoulli beam using the nonlocal elasticity theory for cantilever microtubules.The method of differential quadrature has been used for numerical modeling.Civalek and Demir(2011)developed a nonlocal beam model for the bending analysis of microtubules based on the Euler-Bernoulli beam theory.The size effect is taken into consideration using the Eringen’s nonlocal elasticity theory.

With the development of the material technology,FGMs have been employed in MEMS/NEMS[Witvrouw and Mehta(2005);Lee et al.(2006)]behavior.Because of high sensitivity of MEMS/NEMS to external stimulations,understanding mechanical properties and vibration behavior of them are of signi ficant importance to the design and manufacture of FG MEMS/NEMS.Thus,establishing an accurate model of FG nanobeams is a key issue for successful NEMS design.Niknam and Aghdam(2015)investigated the large amplitude free vibration of Euler-Bernoulli FG nanobeams resting on nonlinear elastic foundation based on the ignorance of the physical neutral axis position.The He’s variational method was used as a semianalytical solution for the nonlinear governing equation.Asghari et al.(2010,2011)studied the free vibration of the FG Euler-Bernoulli microbeams,which has been extended to consider a size-dependent Timoshenko beam based on the modified couple stress theory.The dynamic characteristics of FG beam with power law material graduation in the axial or the transversal directions was examined by Alshorbagy et al.(2011).Ke and Wang(2011)exploited the size effect on dynamic stability of functionally graded Timoshenko microbeams.The free vibration analysis of FG microbeams was presented by Ansari et al.(2011)based on the strain gradient Timoshenko beam theory.It was shown that the value of gradient index plays an important role in the vibrational response of the FG microbeams of lower slenderness ratios and by increasing the length to thickness ratio of the FG microbeam,the value of dimensionless natural frequency tends to decrease for all amounts of the gradient index.Employing modified couple stress theory the nonlinear free vibration of FG microbeams based on von Karman geometric nonlinearity was presented by Ke et al.(2012).It was revealed that both the linear and nonlinear frequencies increase significantly when the thickness of the FGM microbeam was comparable to the material length scale parameter.Eltaher et al.(2012)presented a finite element formulation for free vibration analysis of FG nanobeams based on nonlocal Euler beam theory.In another study,Eltaher et al.(2013a)presented finite element model for free vibration analysis of simplysupported FG nanobeams by using Euler-Bernoulli beam model based on neutral axis position.They also exploited the size-dependent static-buckling behavior of functionally graded nanobeams on the basis of the nonlocal continuum model[Eltaher et al.(2013b)].Using nonlocal Timoshenko and Euler-Bernoulli beam theory,Simsek and Yurtcu(2013)investigated analytically bending and buckling of FG nanobeams by analytical method.All of above mentioned works on FG nanobeams are based on the assumptions that undeformed plane of nanobeam is placed at the mid-plane but due to the variation of material properties along the thickness in FG nanobeams,actually the undeformed plane coincides with the neutral plane rather than the mid-plane.

As one may note, the most cited references dealing with the modeling of micro/nanobeams are based on the assumptions that the material is homogeneous and a very limited literature is available for micro/nano-scale structures using FGM which are based on the assumptions that undeformed plane of nanobeams is placed at the mid-plane.It is found that most of the previous studies on vibration and buckling analysis of FG nanobeams have been conducted based on the ignorance of the physical neutral axis position and various boundary conditions effects.As a result,these studies cannot be utilized in order to thoroughly study the FG nanobeams under investigation.Therefore,there is strong scientific need to understand the vibration and buckling behavior of FG nanobeams in considering the effects of physical neutral axis position and different boundary conditions.Motivated by this fact,in this study,differential transformation method is applied in analyzing vibration and buckling characteristics of size-dependent FG nanobeams considering the right neutral axis position.The superiority of the DTM is its simplicity and good precision and dependence on Taylor series expansion while it takes less time to solve polynomial series.It is different from the traditional high order Taylor’s series method,which requires symbolic computation of the necessary derivatives of the data functions.The Taylor series method computationally takes long time for large orders.With this method,it is possible to obtain highly accurate results or exact solutions for differential equations.

In this work free vibration and buckling analysis of FG nanobeams considering the position of neutral axis are studied.It is assumed that material properties of the beam vary continuously through the beam thickness according to power-law form.Nonlocal Euler-Bernoulli beam model and Eringen’s nonlocal elasticity theory are employed.Governing equations and boundary conditions for the free vibration and buckling of a nonlocal FG beam have been derived via Hamilton’s principle.These equations are solved using DTM and numerical solutions are obtained.The detailed mathematical derivations are presented while the emphasis is placed on investigating the effect of several parameters such as size effects,constituent volume fractions,mode number,slenderness ratios,boundary conditions and small scale on vibration characteristics of FG nanobeams.Comparisons with the results from the existing literature are provided and good agreement between the results of this article and those available in literature validated the presented approach.Numerical results are presented to serve as benchmarks for the application and the design of nanoelectronic and nano-drive devices,nano-oscillators,and nanosensors,in which nanobeams act as basic elements.

2 Theory and formulation

2.1 Nonlocal power-law FG nanobeam equations based on physical neutral axis

One of the most favorable models for FGMs is the power-law model,in which material properties of FGMs are assumed to vary according to a power law about spatial coordinates.The coordinate system for FG nanobeam is shown in Figure 1.The FG nanobeam is assumed to be composed of ceramic and metal and effective material properties of the FG beam such as Young’s modulus Ef,shear modulusand mass density ρfare assumed to vary continuously in the thickness direction(z-axis direction)according to a power function of the volume fractions of the constituents while the Poisson’s ratio is assumed to be constant in the thickness direction.According to the rule of mixture,the effective material properties,Pf,can be expressed as[Simsek and Yurtcu(2013)]:

where Pm,Pc,Vmand Vcare the material properties and the volume fractions of the metal and the ceramic constituents related by:

The volume fraction of the ceramic constituent of the beam is assumed to be given by:

Here p is the non-negative variable parameter(power-law exponent)which determines the material distribution through the thickness of the beam.Therefore,from

Eqs.(1)-(2),the effective material properties of the FG nanobeam can be expressed as follows:

According to this distribution,bottom surface(z=-h/2)of functionally graded beam is pure metal,whereas the top surface(z=h/2)is pure ceramics.Based on the physical neutral surface concept introduced by Zhang and Zhou(2008),the physical neutral surface of FGM beam is given by:

It can be seen that the physical neutral surface and the geometric middle surface are the same in a homogeneous isotropic beam.

2.2 Kinematic relations

Under the physical neutral surface concept and the Euler-Bernoulli nanobeam model,the displacement field at any point of the beam can be written as

where t is time,u and w are displacement components of the mid-plane along x and z directions,respectively.By assuming the small deformations,the only nonzero strain of the Euler-Bernoulli beam theory is:

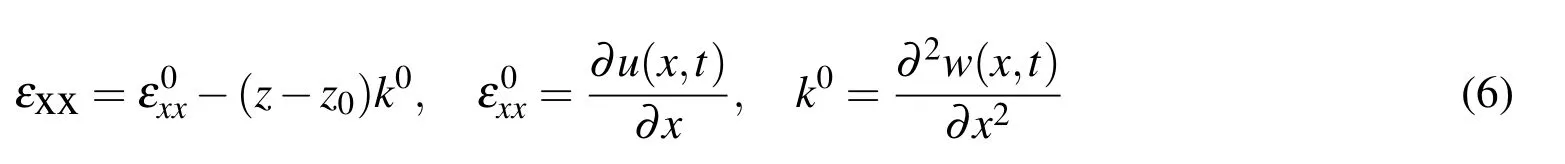
Figure 1:Typical functionally graded beam with Cartesian coordinates.

Here U is strain energy,T is kinetic energy and Wextis work done by external forces.The virtual strain energy can be calculated as:

Substituting Eq.(6)into Eq.(8)yields:

In which N,M are the axial force and bending moment respectively.These stress resultants used in Eq.(9)are defined as:

The kinetic energy for Euler-Bernoulli beam can be written as:

Also the virtual kinetic energy is:

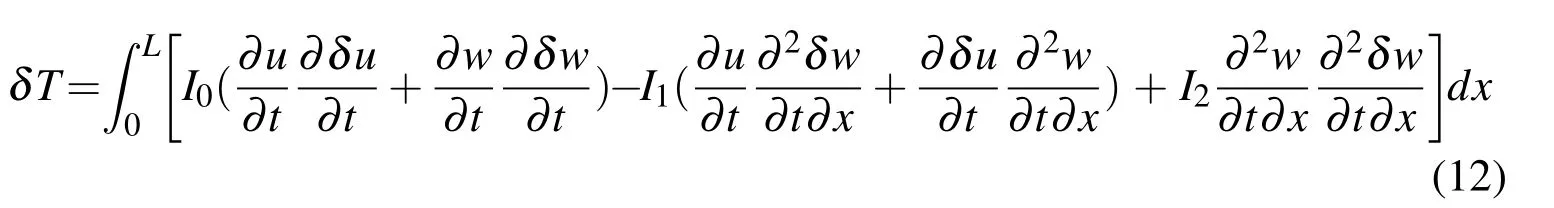
where(I0,I1,I2)are the mass moment of inertias,defined as follows:

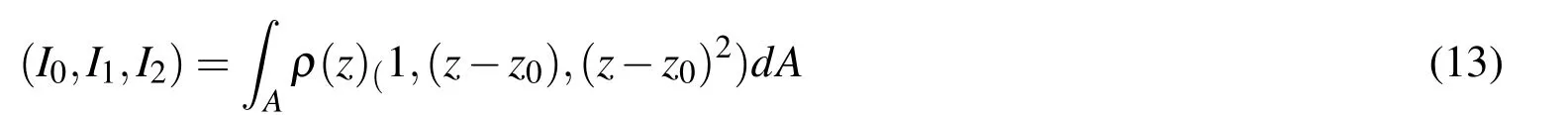
The first variation of external forces of the beam can be written in the form:

Under the following boundary conditions:

2.3 The nonlocal elasticity model for FG nanobeam

Based on Eringen nonlocal elasticity model[Eringen&Edelen(1972)],the stress at a reference point x in a body is considered as a function of strains of all points in the near region.This assumption is in agreement with experimental observations of atomic theory and lattice dynamics in phonon scattering in which for a homogeneous and isotropic elastic solid the nonlocal stress-tensor components σijat any point x in the body can be expressed as:

The meaning of Eq.(17)is that the nonlocal stress at point x is the weighted average of the local stress of all points in the neighborhood of x,the size of which is related to the nonlocal kernel.Hereis the Euclidean distance and τ is a constant given by:

which represents the ratio between a characteristic internal length,a(such as lattice parameter,C-C bond length and granular distance)and a characteristic external one,l(e.g.crack length,wavelength)through an adjusting constant,e0,dependent on each material.The magnitude of e0is determined experimentally or approximated by matching the dispersion curves of plane waves with those of atomic lattice dynamics.According to Eringen and Edelen(1972)for a class of physically admissible kernelit is possible to represent the integral constitutive relations given by Eq.(17)in an equivalent differential form as:

where∇2is the Laplacian operator.Thus,the scale length e0a takes into account the size effect on the response of nanostructures.For an elastic material in the one dimensional case,the nonlocal constitutive relations may be simplified as:

where σ and ε are the nonlocal stress and strain,respectively.E is the Young’s modulus.For Euler-Bernoulli nonlocal FG beam,Eq.(21)can be written as:

In which the cross-sectional rigidities are defined as follows:

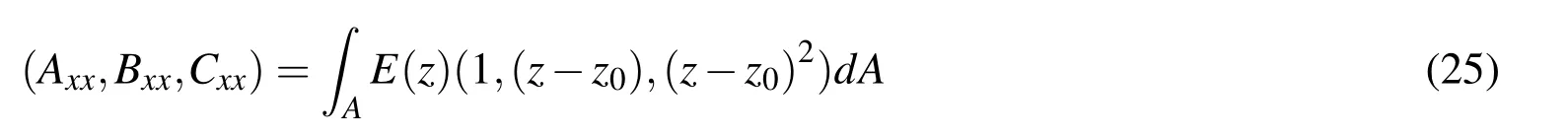
The explicit relation of the nonlocal normal force can be derived by substituting for the second derivative of N from Eq.(15a)into Eq.(23)as follows:

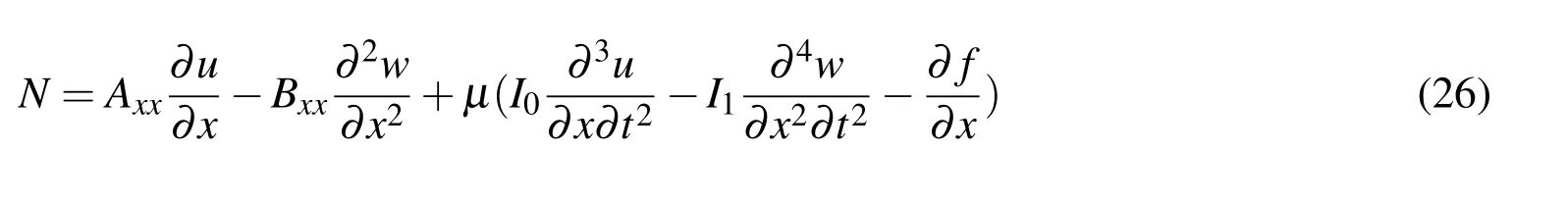
Also the explicit relation of the nonlocal bending moment can be derived by substituting for the second derivative of Mfrom Eq.(15b)into Eq.(24)as follows:

The nonlocal governing equations of Euler-Bernoulli FG nanobeam in terms of the displacement can be derived by substituting for Nand Mfrom Eqs.(26)and(27),respectively,into Eq.(15)as follows:

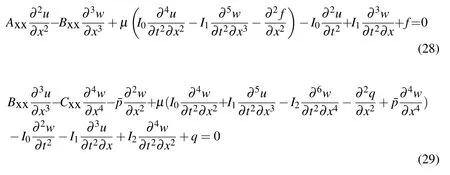
When the FG nanobeam vibrates with a natural frequency ω,it is possible to separate the time dependency by expressing the displacement parameters in the following form:

Substituting harmonic vibration modes,Eqs.(30)and(31),into Eqs.(28)and(29)leads to a time independent governing equation as follows:

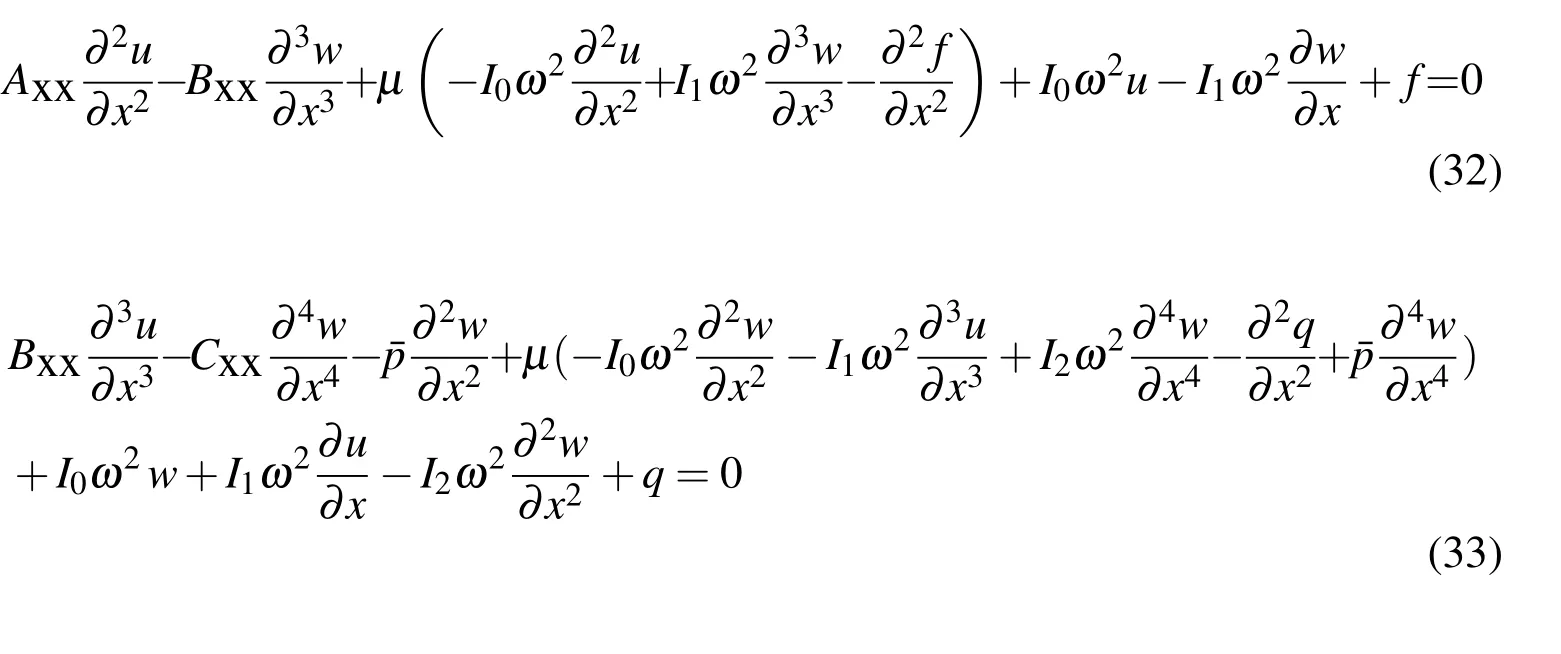
3 Implementation of differential transform method

Generally,it is rather difficult to derive an analytical solution for Eqs.(32)and(33)due to the nature of non-homogeneity.In this circumstance,the DTM is employed to translate the governing equations into a set of ordinary equations.First,the procedure of differential transform method is briefly reviewed.The differential transforms method provides an analytical solution procedure in the form of polynomials to solve ordinary and partial differential equations.In this method,differential transformation of kth derivative function y(x)and differential inverse transformation of Y(k)are respectively defined as follows[Abdel-Halim Hassan(2002)]:

In which y(x)is the original function and Y(k)is the transformed function.Consequently from equations(34,35)we obtain:

Equation(36)reveals that the concept of the differential transformation is derived from Taylor’s series expansion.In real applications the function y(x)in equation(36)can be written in a finite form as:

where U[k]and W[k]are the transformed functions of u,w,respectively.

Table 1:Some of the transformation rules of the one-dimensional DTM[Chen and Ju(2004)].

Table 2:Transformed boundary conditions(B.C.)based on DTM[Chen and Ju(2004)].

Additionally,the differential transform method is applied to various boundary conditions by using the theorems introduced in Table 2 and the following transformed boundary conditions are obtained.

·Simply supported-Simply supported:

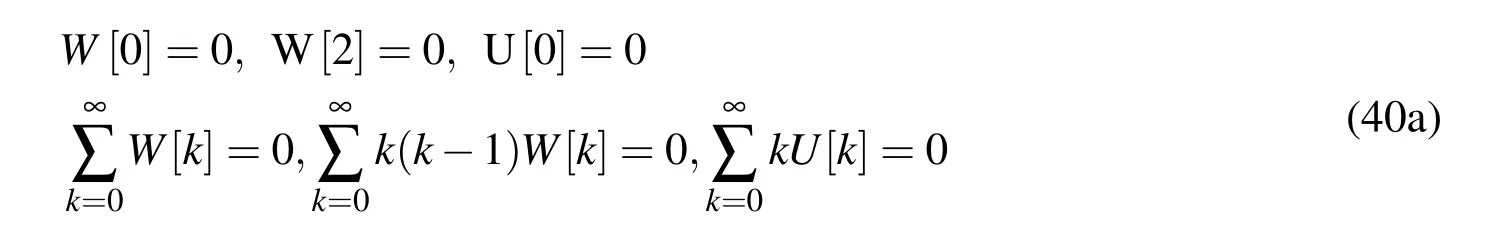
·Clamped-Clamped:

·Clamped-Simply supported:

·Clamped-Free:

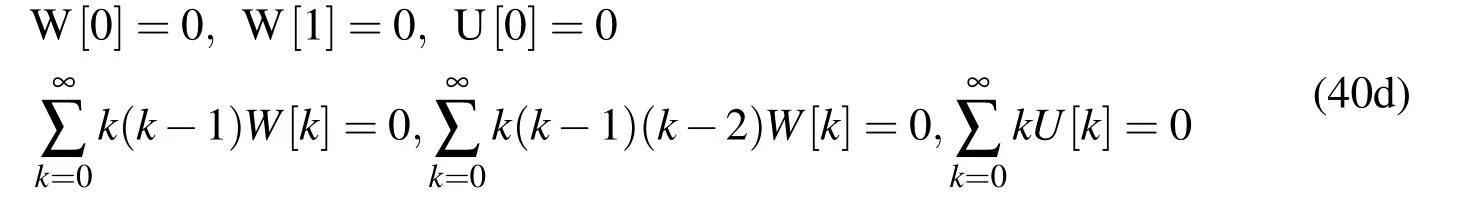
By using Eqs.(38)and(39)together with the transformed boundary conditions one arrives at the following eigenvalue problem:

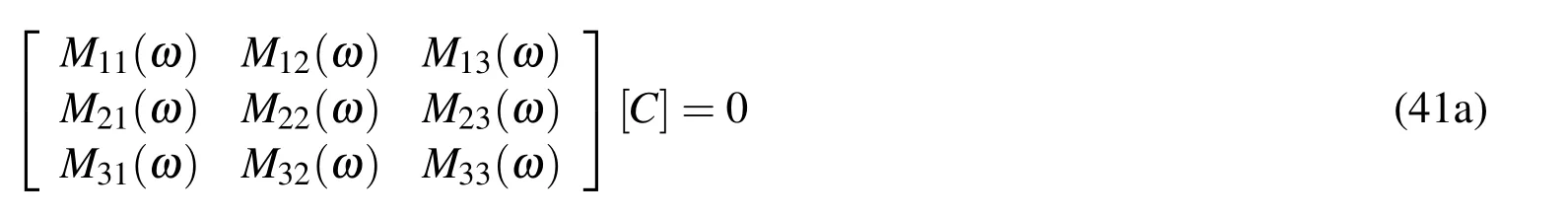
where[C]correspond to the missing boundary conditions at x=0 and Mij(ω)are polynomials in terms of ω.For the non-trivial solutions of Eq.(41a),it is necessary that the determinant of the coefficient matrix is equal to zero:

Solution of Eq.(41b)is simply a polynomial root finding problem.In the present study,the Newton-Raphson method is used to solve the governing equation of the non-dimensional natural frequencies.Solving equation(41b),the ithestimated eigenvalue for nth iterationmay be obtained and the total number of iterations is related to the accuracy of calculations which can be determined by the following equation:

In this study ε=0.0001 considered in procedure of finding eigenvalues which results in 4 digit precision in estimated eigenvalues.Further a Matlab program has been developed according to DTM rule stated above,in order to find eigenvalues.As mentioned before,DT method implies an iterative procedure to obtain the highorder Taylor series solution of differential equations.The Taylor series method requires a long computational time for large orders,whereas one advantage of employing DTM in solving differential equations is a fast convergence rate and a small calculation error.

4 Numerical results and discussions

Through this section,a numerical testing of the procedure as well as parametric studies are performed in order to establish the validity and usefulness of the DTM approach.The effect of neutral axis position on the natural frequencies and buckling load of FG size-dependent nanobeam is presented.The functionally graded nanobeam is composed of steel and alumina where its properties are given in Table 3.The bottom surface of the beam is pure steel,whereas the top surface is pure alumina.The beam geometry has the following dimensions:L(length)=10,000 nm,b(width)=1000 nm and h(thickness)=100 nm.

4.1 Convergence and correctness study of the solution method

In order to show that differential transform method is an effective and reliable tool for examining the vibration and buckling characteristics of nanobeams,a FG nanobeam composed of a ceramic-metal pair of materials(steel and alumina)is considered.Relation described in equation(43)is performed in order to calculate the non-dimensional natural frequencies.

where I=bh3/12 is the moment of inertia of the cross section of the beam.Table 4 tabulates the convergence of DT method for the first four frequencies of FG nanobeams with various gradient indexes.It is found that in DT method after a certain number of iterations eigenvalues converged to a value with good precision,so the number of iterations is important in DT method convergence.According to Table 4 the first natural frequency converged after 19 iterations(k)with 4 digit precision while the 2nd,3rd and 4th frequencies converged after 29,39 and 47 iterations respectively.

Table 3:Material properties of the FGM constituents[Asghari et al.(2011)].

After looking into the satisfactory results for the convergence of frequencies,one may compare the nondimensional frequencies of FG nanobeam associated with dif-ferent boundary conditions,nonlocal parameter,slenderness ratios and constituent volume fraction exponents.To demonstrate the correctness of present study the results for FG nanobeam are compared with the results of FG nanobeams available in the literature.Table 5 compares the semi-analytical results of the present study obtained based on physical neutral axis position(NA)and the results for the simply supported-simply supported(S-S)FG nanobeam with various nonlocal parameter and constituent volume fraction exponents presented by Eltaher et al.(2012)which has been obtained by using finite element method.One may clearly notice here that the fundamental frequency parameters obtained in the present investigation are in approximately close enough to the results provided in these literatures and thus validates the proposed method of solution.

4.2 Vibration analysis

After validating the approaches,in this section some parametric studies are conducted in order to examine the influences of various FG nanobeam parameters such as constituent volume fractions,nonlocal parameters,slenderness ratios and boundary conditions on the natural frequencies of the size-dependent FG nanobeam model based on neutral axis position(NA)and central axis position(CA).Here after,to better extract the influence of the neutral axis position on the vibrational behavior of the FG nanobeams,the normalized form of the nonlinear natural frequencies as specified in Eq.(43),are presented in the numerical results.

The effect of neutral axis position on first four nondimensional frequencies of FG nanobeam with various nonlocal parameters and constituent volume fractions is presented in Tables 5-8.In these tables the first four nondimensional frequencies of FG nanobeam for different boundary conditions such as simply supported-simply supported(S-S),clamped-clamped(C-C),clamped-simply supported(C-S)and clamped-free(C-F)are tabulated based on neutral axis position and midplane position calculations.The nonlocal parameter µ ranges from 0 to 4 and the material distribution parameter p ranges from 0 to 10.When these two parameters vanish(µ=0,p=0),the classical isotropic beam theory is rendered.Fixing the nonlocal parameter µ and varying the material distribution parameter p results in a significant change in the natural frequencies.

As it can be seen from Table 5,for a simply supported FG nanobeam by increasing the nonlocal parameter from 0 to 4 at a constant material graduation parameter,the first natural frequency decreases about 15%.Whereas,by increasing the nonlocal parameter the difference between the natural frequencies obtained based on central axis and neutral axis decreases.It can be noticed from Table 5 that,the neutral axis position has a significant effect on the natural frequencies of simply supported FG nanobeam.

For the case in hand,changing the material parameter p from 0 to 10 results in decreasing the natural frequencies,as can be seen in Tables 5-8.It should be noted that as the nonlocal parameter increases, the first natural frequency increases, which highlights the significance of the nonlocal effect.One may clearly notice here that,the calculated frequencies based on central axis position are overestimated compared to those obtained based on neutral axis position.

It is also observed that,by increasing the nonlocal parameter from 0 to 4,the first nondimensional frequency decreases about 15%at a constant material distribution for S-S,C-C and C-S boundary conditions while the trend for the 2nd,3rd and the 4th nondimensional frequencies are decreasing about 38%,54%and 64%respectively.On the other hand,for the C-F boundary condition the first natural frequency increases about 1.8%and the 2nd,3rd and the 4th nondimensional frequencies decreases about 21%,40%and 55%respectively,at a fixed material distribution.In this study,increasing the material distribution parameter at a constant nonlocal parameter causes the decreasing in all frequencies,due to increasing the ceramics phase constituent,and hence,stiffness of the beam.By changing the material distribution parameter from 0 to 10,the first four frequencies reduced about 40-45%.This result indicates that,the effect of material graduation index strengthen the nanobeam by increasing the ceramics constituent phase.This trend is observable in other edge conditions of C-C,C-S and C-F.Lastly the effect of nonlocal parameter and material distribution on the nondimensional frequency of FG nanobeam with various edge conditions are presented in Tables 6-8.For a C-C nanobeam,as the nonlocal parameter changes from 0 to 4,the first natural frequency decreases about 18%,as can be noted from the Table 6.

The effect of nonlocal and material distribution parameter on the frequencies of C-S FG nanobeam is illustrated in Table 7.It is observed that,by increasing the nonlocal parameter from 0 to 4,the first natural frequency decreases about 17%at a fixed material graduation parameter.

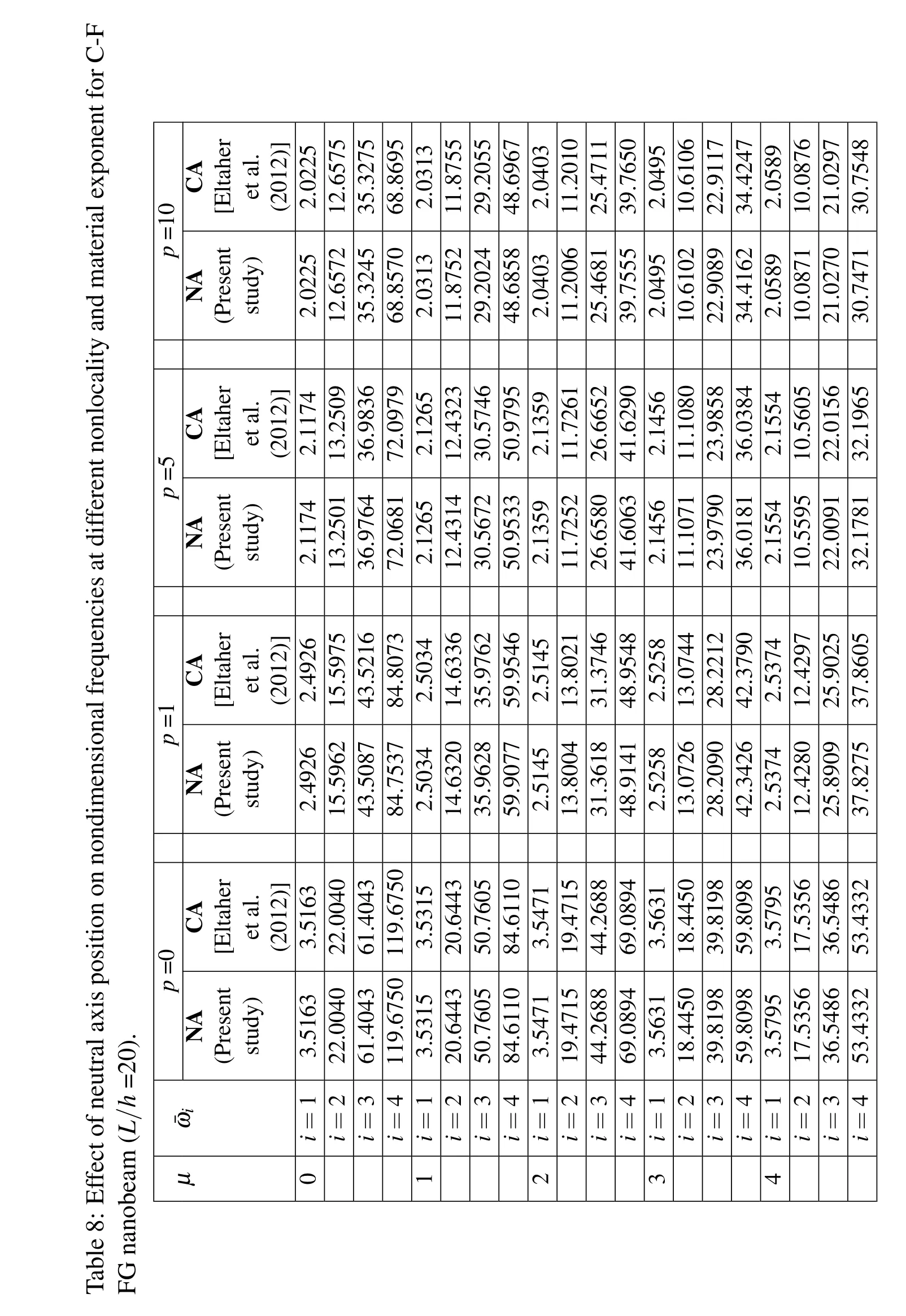
The nondimensional frequencies of the C-F FG nanobeam,versus the nonlocal and material distribution parameters,are tabulated in Table 8.It is observed that,by increasing the nonlocal parameter from 0 to 4,the first natural frequency increases about 1.8%at a constant material distribution parameter.It can be noticed that,the neutral axis position has negligible effect on the first natural frequency of C-F FG nanobeam.For all boundary conditions,the results show a decreasing about 42%in first four natural frequencies of FG nanobeams at a fixed nonlocal parameter,where the material distribution parameter changes from 0 to 10.

Figure 2:Variation of the first dimensionless frequency of FG nanobeam with material graduation for various boundary conditions(L/h=100).

Figure 2 demonstrate the variation of nondimensional fundamental frequency with changing the material graduation parameter for various nonlocal parameters of FG nanobeam with different boundary conditions.As presented in this figure,for all boundary conditions by increasing material graduation parameter,the first dimensionless frequency decreases.It is also observed that,in the case of C-F edge condition,increasing material graduation parameter at constant nonlocal parameter ofµ=0has non-sensitive effect on frequency parameter.

4.3 Buckling analysis

For the purpose of verification,the present model is used to find the buckling load for a S-S FG nanobeam modeled based on neutral axis position where the nonlocal effect is taken into consideration.The obtained results by DTM are compared with the results available in literature.To the author’s best knowledge no study reported on the buckling analysis of FG nanobeams based on neutral axis position yet.This comparison is presented in Table 9 for the length-to-thickness ratio of 100 while varying the nonlocal parameter µ from 0 to 4.As can be seen from Table 9,the obtained results are in a good agreement with those of Reddy(2007)which has been obtained by analytical method.The buckling load is non-dimensionalized as follows:

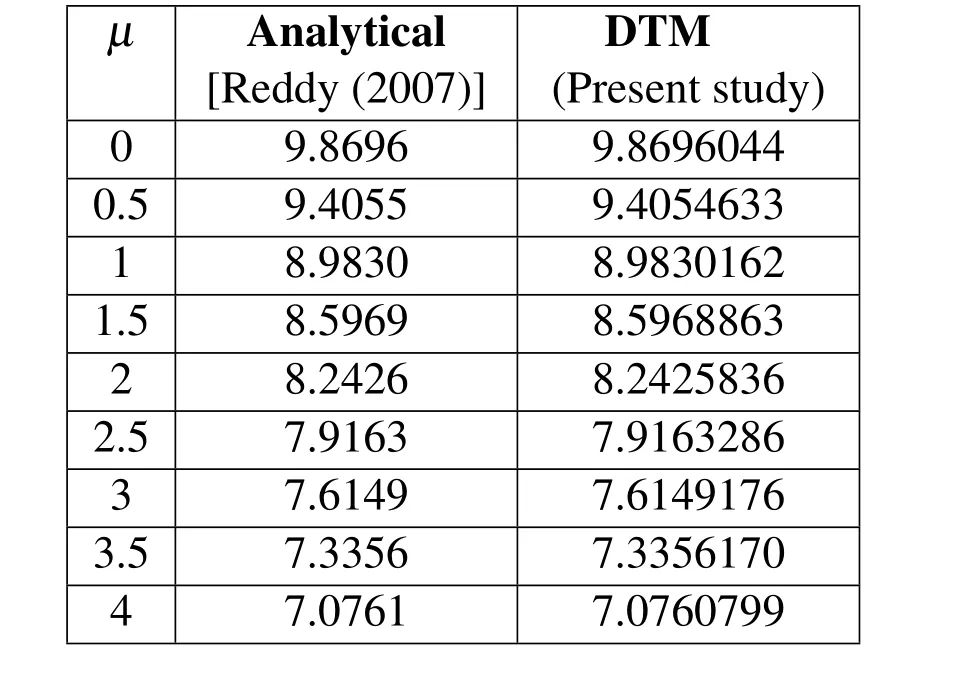
Table 9:Comparison of the nondimensional buckling load for a simply supported nanobeam(L/h=100).

For all edge conditions,the nondimensional buckling load is presented considering the physical neutral axis position in Tables 10-12 as the nonlocal parameter μ varies from 0 to 5 and the material distribution parameter p ranges from 0 to 5.

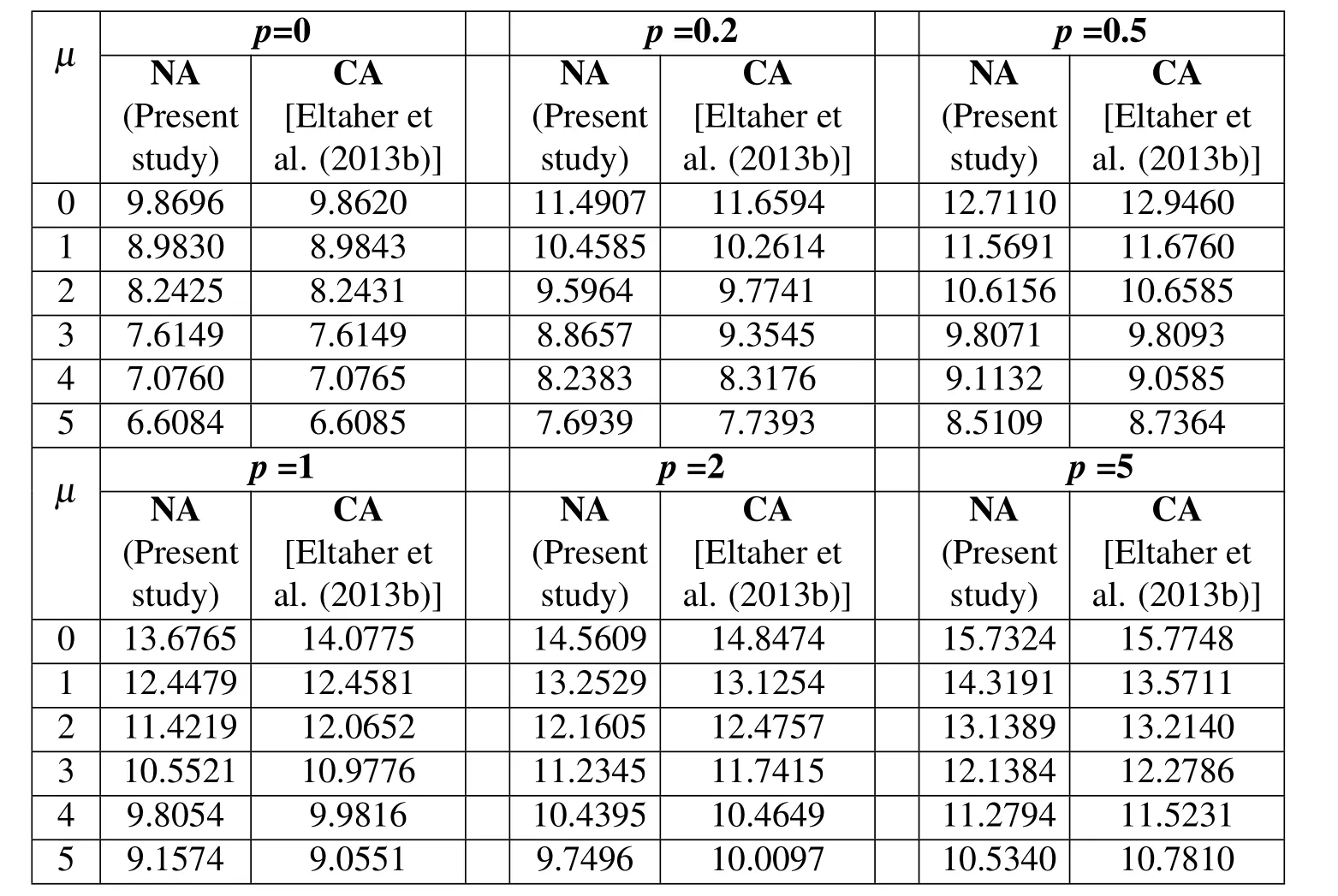
Table 10:Effect of neutral axis position on nondimensional buckling load of S-S FG nanobeams with different nonlocality and material exponents(L/h=100).

By changing the material distribution parameter p,a significant change in the buckling load is observed at a fixed nonlocal parameter.For the case in hand,changing the material parameter p from 0 to 5 results in an increase in the buckling load of about 60%,as can be seen from Tables 10-12.It is also concluded that as the nonlocal parameter increases,the buckling load decreases,which highlight the significance of the nonlocal effect.

Effect of neutral axis position on nondimensional buckling load for all boundary conditions of FG nanobeam is significant.It can be noticed from Tables 10-12 that the calculated buckling load based on central axis position is underestimated compared to one obtained based on neutral axis position.

For a FG nanobeam with S-S edge condition,as the nonlocal parameter increases from 0 to 5,the buckling load decreases about 50%,as presented in Table 10.In addition,by increasing the material distribution parameter form 0 to 5,the buckling load increases about 60%.The nondimensional buckling load of the C-C FG nanobeam,versus the nonlocal and material distribution parameters,is tabulated in Table 11.It is observed that,by increasing the nonlocal parameter from 0 to 5,thebuckling load decreases about 66%at a constant material distribution parameter p.By changing the material distribution parameter form 0 to 5,the buckling load is increased by about 60%.Moreover the effect of nonlocality and material distribution on the buckling load of FG nanobeam with C-S edge condition is illustrated in Table 12.It is observed that,by increasing the nonlocal parameter from 0 to 5,the buckling load decreases about 50%at a fixed material graduation parameter.Whereas,by changing the material distribution parameter from 0 to 5,the variation of the buckling load is similar to those of S-S and the C-C FG nanobeams.Figure 3 presents the nondimensional buckling load for a FG nanobeam with varying material distribution parameter for various nonlocal parameters and different edge conditions.This observation is found to be similar for different values of nonlocal parametersµ=1,2,3,4 and 5 as shown in Figure 3.Conclusions drawn from Tables 10-12 can be easily noted from these figures.

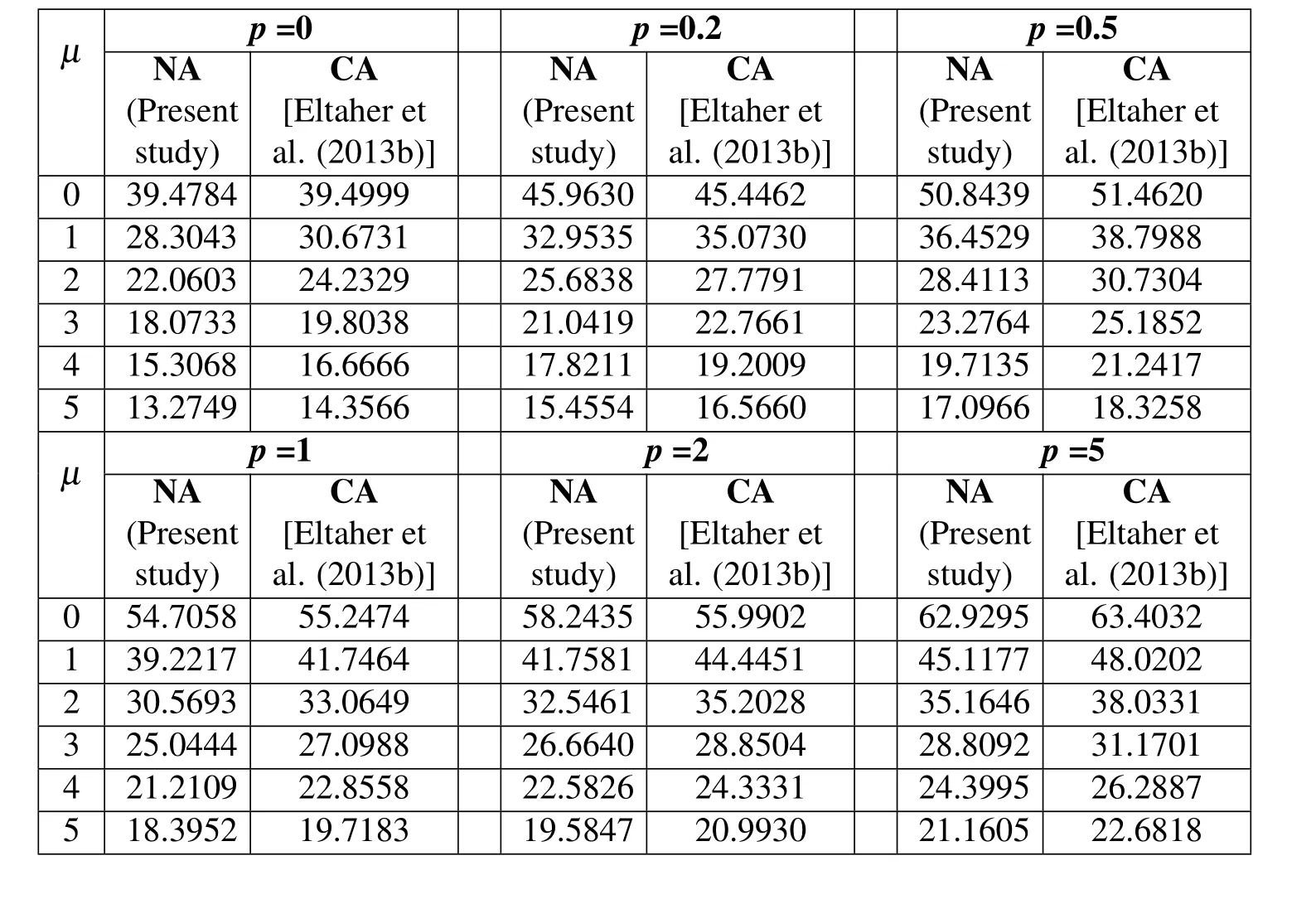
Table 11:Effect of neutral axis position on nondimensional buckling load of C-C FG nanobeams with different nonlocality and material exponents(L/h=100).

Figure 3:Variation of the nondimensional buckling load with material graduation for different boundary condition(L/h=100).

Table 12:Effect of neutral axis position on nondimensional buckling load of C-S FG nanobeams with different nonlocality and material exponents(L/h=100).

5 Conclusions

In this paper,free vibration and buckling analysis of functionally graded sizedependent nanobeams modeled based on physical neutral axis position is investigated within the framework of a semi-analytical technique called the differential transform method.The material properties of FG nanobeams vary continuously in the thickness direction according to the power-law form.Nonlocal elasticity equations of Eringen are applied in the formulations to achieve the vibration and buckling characteristics of FG nanobeam through Hamilton’s principle.The good agreement between the results of this article and those available in literature validated the presented approach.Several important aspects such as material volume fraction index,nonlocal parameter, mode number and as well as various edge conditions which have impacts on natural frequencies of FG nanobeams are investigated and discussed in detail.Numerical results reveal that the neutral axis position play an important role on the vibration and buckling behavior of a FG nanobeam and the calculated frequencies based on geometrical central axis position is overestimated.Numerical results are presented to serve as benchmarks for future analyses of FG nanobeams.

Alshorbagy,A.E.;Eltaher,M.A.;Mahmoud,F.F.(2011):Free vibration characteristics of a functionally graded beam by finite element method.Applied Mathematical Modelling,vol.35,pp.412-425.

Ansari,R.;Gholami,R.;Sahmani,S.(2011):Free vibration analysis of sizedependent functionally graded microbeams based on the strain gradient Timoshenko beam theory.Composite Structures,vol.94,pp.221-8.

Asghari,M.;Ahmadian,M.T.;Kahrobaiyan,M.H.;Rahaeifard,M.(2010):On the size-dependent behavior of functionally graded micro-beams.Materials and Design,vol.31,pp.2324-2329.

Asghari,M.;Rahaeifard,M.;Kahrobaiyan,M.H.;Ahmadian,M.T.(2011):The modified couple stress functionally graded Timoshenko beam formulation.Materials and Design,vol.32,pp.1435-1443.

Aydogdu,M.(2009):A general nonlocal beam theory:its application to nanobeam bending,buckling and vibration.Physica E:Low-dimensional Systems and Nanostructures,vol.41,no.9,pp.1651-1655.

Baughman,R.H.;Zakhidov,A.A.;de Heer,W.A.(2002):Carbon nanotubesthe route toward applications.Science,vol.297,no.5582,pp.787-792.

Chen,C.O.K.;Ju,S.P.(2004):Application of differential transformation to transient advective-dispersive transport equation.Applied Mathematics and Computation,vol.155,no.1,pp.25-38.

Civalek,O.;Demir,C.;Akgoz,B.(2010):Free vibration and bending analyses of cantilever microtubules based on nonlocal continuum model.Mathematical and Computational Applications,vol.15,no.2,pp.289-298.

Civalek,Ö.;&Demir,Ç.(2011):Bending analysis of microtubules using nonlocal Euler-Bernoulli beam theory.Applied Mathematical Modelling,vol.35,no.5,pp.2053-2067.

Ebrahimi,F.;Rastgoo,A.(2008a):Free vibration analysis of smart annular FGM plates integrated with piezoelectric layers.Smart Materials and Structures,vol.17,no.1,015044.

Ebrahimi,F.;Rastgoo,A.(2008b):An analytical study on the free vibration of smart circular thin FGM plate based on classical plate theory.Thin-Walled Structures,vol.46,no.12,pp.1402-1408.

Ebrahimi,F.;Rastgoo,A.;Atai,A.A.(2009a):A theoretical analysis of smart moderately thick shear deformable annular functionally graded plate.European Journal of Mechanics-A/Solids,vol.28,no.5,pp.962-973.

Ebrahimi,F.;Naei,M.H.;Rastgoo,A.(2009):Geometrically nonlinear vibration analysis of piezoelectrically actuated FGM plate with an initial large deformation.Journal of mechanical science and technology,vol.23,no.8,pp.2107-2124.

Eltaher,M.A.;Emam,S.A.;Mahmoud,F.F.(2012):Free vibration analysis of functionally graded size-dependent nanobeams.Applied Mathematics and Computation,vol.218,no.14,pp.7406-7420.

Eltaher,M.A.;Alshorbagy,A.E.;Mahmoud,F.F.(2013a):Determination of neutral axis position and its effect on natural frequencies of functionally graded macro/nanobeams.Composite Structures,vol.99,pp.193-201.

Eltaher,M.A.;Emam,S.A.;Mahmoud,F.F.(2013b):Static and stability analysis of nonlocal functionally graded nanobeams.Composite Structures,vol.96,pp.82-88.

Eringen,A.C.;Edelen,D.G.B.(1972):Nonlocal elasticity.International Journal of Engineering Sciences,vol.10,no.3,pp.233-48.

Eringen,A.C.(1972b):Nonlocal polar elastic continua.International Journal of Engineering Sciences,vol.10,no.1,pp.1-16.

Eringen,A.C.(1983):On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves.Journal of Applied Physics,vol.54,no.9,pp.4703-4710.

Hassan,I.A.H.(2002):On solving some eigenvalue problems by using a differential transformation.Applied Mathematics and Computation,vol.127,no.1,pp.1-22.

Iijima,S.(1991):Helical microtubules of graphitic carbon.Nature,vol.354,no.6348,pp.56-58.

Ke,L.L.;Wang,Y.S.(2011):Size effect on dynamic stability of functionally graded microbeams based on a modified couple stress theory.Composite Structures,vol.93,pp.342-350.

Ke,L.L.;Wang,Y.S.;Yang,J.;Kitipornchai,S.(2012):Nonlinear free vibration of size dependent functionally graded microbeams.International Journal of Engineering Sciences,vol.50,pp.256-67.

Lee,Z.;Ophus,C.;Fischer,L.M.;Nelson-Fitzpatrick,N.;Westra,K.L.;

Evoy,S.et al.(2006):Metallic NEMS components fabricated from nanocomposite Al-Mo films.Nanotechnology,vol.17,no.12,pp.3063-70.

Maranganti,R.;Sharma,P.(2007):Length scales at which classical elasticity breaks down for various materials.Physical review letters,vol.98,no.19,195504.

Niknam,H.;Aghdam,M.M.(2015):A semi analytical approach for large amplitude free vibration and buckling of nonlocal FG beams resting on elastic foundation.Composite Structures,vol.119,pp.452-462.

Peddieson,J.;Buchanan,G.R.;McNitt,R.P.(2003):Application of nonlocal continuum models to nanotechnology.International Journal of Engineering Science,vol.41,no.3,pp.305-312.

Phadikar,J.K.;Pradhan,S.C.(2010):Variational formulation and finite element analysis for nonlocal elastic nanobeams and nanoplates.Computational Materials Science,vol.49,no.3,pp.492-499.

Pradhan,S.C.;Murmu,T.(2010):Application of nonlocal elasticity and DQM in the flapwise bending vibration of a rotating nanocantilever.Physica E:Lowdimensional Systems and Nanostructures,vol.42,no.7,pp.1944-1949.

Reddy,J.N.(2007):Nonlocal theories for bending,buckling and vibration of beams.International Journal of Engineering Science,vol.45,no.2,pp.288-307.

Simsek,M.;Yurtcu,H.H.(2013):Analytical solutions for bending and buckling of functionally graded nanobeams based on the nonlocal Timoshenko beam theory.Compos.Struct.,vol.97,pp.378-386.

Tauchert,T.R.(1974):Energy principles in structural mechanics.Library of Congress Cataloging in Publication Data.

Wang,X.;Cai,H.(2006):Effects of initial stress on non-coaxial resonance of multi-wall carbon nanotubes.Acta materialia,vol.54,no.8,pp.2067-2074.

Wang,Q.(2005):Wave propagation in carbon nanotubes via nonlocal continuum mechanics.Journal of Applied Physics,vol.98,no.12,124301.

Wang,Q.;Varadan,V.K.(2006):Vibration of carbon nanotubes studied using nonlocal continuum mechanics.Smart materials and structures,vol.15,no.2,pp.659.

Wang,Q.;Liew,K.M.(2007):Application of nonlocal continuum mechanics to static analysis of micro-and nano-structures.Physics Letters A,vol.363,no.3,pp.236-242.

Witvrouw,A.;Mehta,A.(2005):The use of functionally graded poly-SiGe layers for MEMS applications.Funct Graded Mater,vol.492,pp.255-260.

Zhang,Y.Q.;Liu,G.R.;Wang,J.S.(2004):Small-scale effects on buckling of multiwalled carbon nanotubes under axial compression.Physical review B,vol.70,no.20,205430.

Zhang,D.G.;Zhou,Y.H.(2008):A theoretical analysis of FGM thin plates based on physical neutral surface.Computational Materials Science,vol.44,no.2,pp.716-720.