Investigation on a Two-dimensional Generalized Thermal Shock Problem with Temperature-dependent Properties

Tianhu He,Yongbin Maand Shuanhu Shi

Investigation on a Two-dimensional Generalized Thermal Shock Problem with Temperature-dependent Properties

Tianhu He1,2,3,Yongbin Ma2,3and Shuanhu Shi3

The dynamic response of a two-dimensional generalized thermoelastic problem with temperature-dependent properties is investigated in the context of generalized thermoelasticity proposed by Lord and Shulman.The governing equations are formulated,and due to the nonlinearity and complexity of the governing equations resulted from the temperature-dependent properties,a numerical method,i.e.,finite element method is adopted to solve such problem.By means of virtual displacement principle,the nonlinear finite element equations are derived.To demonstrate the solution process,a thermoelastic half-space subjected to a thermal shock on its bounding surface is considered in detail.The nonlinear finite element equations for this problem are solved directly in time domain.The variations of the considered variables are obtained and illustrated graphically.The results show that the effect of the temperature-dependent properties on the considered variables is to reduce their magnitudes,and taking the temperature-dependence of material properties into consideration in the investigation of generalized thermoelastic problem has practical meaning in predicting the thermoelastic behaviors accurately.It can also be deduced that directly solving the nonlinear finite element equations in time domain is a powerful method to deal with the thermoelastic problems with temperature-dependent properties.

generalized thermoelasticity,thermal shock,finite element method,thermal relaxation,temperature-dependent properties.

1 Introduction

In the classical coupled thermoelasticity proposed by[Biot(1956)],due to the diffusive heat conduction equation,it predicts an infinite speed for heat propagating in elastic medium,which is physically unrealistic.To eliminate such inherentparadox,the generalized thermoelastic theories have been introduced by[Lord and Shulman(1967)]and[Green and Lindsay(1972)]since 1960’s,which are abbreviated as L-S theory and G-L theory respectively.In L-S theory,a new wave-type heat conduction law was postulated to replace the classical Fourier’s law.This new law is the same as that suggested by [Cattaneo(1958)]and[Vernotte(1961)],which contains the heat flux vector as well as its time derivative and also contains a new constant that acts as a relaxation time.The L-S theory was later extended by[Dhaliwal and Sherief(1980)]to the case of anisotropic media.The G-L theory modified both the energy equation and the Duhamel-Neumann relation by introducing two relaxation times,and also modified the heat conduction equation by introducing the temperature-rate term,which doesn’t violate the Fourier’s heat conduction law when the considered body has a center of symmetry.In both theories,the governing equations are of hyperbolic type,which can describe the so-called second sound effect,i.e.,heat propagates in medium with a finite speed.

Based on the generalized theories,a great deal of attention has been paid to investigate generalized dynamic problems.[Sherief and Dhaliwal(1981)]concerned a one-dimensional thermal shock problem by the Laplace transform technique and its inverse transform.[Sherief and Anwar(1994)]studied the thermoelastic problem of a homogeneous isotropic thick plate of in finite extent with heating on a part of the surface by state space approach together with Laplace and Fourier integral transforms and their inverse counterparts.[Dhaliwal and Rokne(1989)]solved a thermal shock problem of a half-space with its plane boundary either held rigidly fixed or stress-free and an approximate small-time solution was obtained by using the Laplace transform method.Chen and Weng proposed a hybrid Laplace transform- finite element method to investigate the coupled transient behavior of generalized thermoelastic problems,and they used this method to study the generalized thermoelastic response of a square cylinder with an elliptical hole[Chen and Weng(1988)]and an axisymmetric circular cylinder[Chen and Weng(1989)]respectively.Later,[He,Tian and Shen(2002)]and[Aouadi(2007)]developed this method to deal with a two-dimensional problem of a thick piezoelectric plate with in finite extent and a two-dimensional problem of a half-space in electromagnetothermoelasticity respectively.

The above investigations were carried out under the assumption that the material properties are temperature-independent,which limit the applicability of the obtained solutions to certain ranges of temperature.In general,material properties such as the modulus of elasticity,Poisson’s ratio,the coefficient of thermal expansion and the thermal conductivity etc.would vary with temperature,which in turn influence the thermoelastic coupling behaviors.To explore the effect of temperature-dependent properties on generalized dynamic problems,[Ezzat,El-Karamany and Samaan(2004)]investigated thermoelastic problems with the modulus of elasticity dependent with temperature.[Aouadi(2006)]studied the effect of temperature dependence of the modulus of elasticity on the solutions in generalized thermo-piezoelectricity.[Othman and Song(2008);Othman and Kumar(2009)]worked on the reflection of magneto-thermoelasticity waves under the effect of temperature-dependent properties in generalized thermoelasticity.[Othman and Lotfy(2009)]dealt with a two-dimensional problem of generalized magnetothermoelasticity with temperature-dependent elastic moduli for different theories.In their works,the properties were assumed as a linear function of reference temperature instead of real-time temperature.

In present work,a two-dimensional generalized thermoelastic problem with temperature-dependent properties is investigated in the context of L-S theory.The properties are assumed to be dependent with the real-time temperature instead of the reference temperature,which result in a system of nonlinear governing equations.To solve such nonlinear generalized thermoelastic problem, finite element method is adopted,and the nonlinear finite element equations are derived by means of virtual displacement principle.To set an example,a thermoelastic half-space subjected to a thermal shock is concerned in detail.It should be noted that the derived nonlinear finite element equations are solved directly in time domain.

2 Basic Equations

In the absence of body force and inner heat source,the L-S type generalized thermoelastic governing equations are

In the above equations,a superimposed dot denotes the derivative with respect to time,a comma followed by a suffix denotes material derivative and the summation convention is used.σijare the components of the stress tensor,εijthe components of the strain tensor,uithe components of displacement vector,cijklthe elastic constants,aijthe thermal moduli,κijthe coefficients of thermal conductivity,η the entropy density,qithe components of heat flux vector,τ the thermal relaxation time,θ=T−T0the temperature increment,T the absolute temperature,T0the initial reference temperature,ν=ρCE?T0,ρ the mass density,CEthe specific heat at constant strain.Once τ=0,the L-S theory reduces to the classical coupled thermoelasticity.

For the isotropic case,Eqs.(2)and(7)reduce to

where λ,µ are Lame’s constants,e=εkkis the cubical dilatation,γ=(3λ +2µ)αtand αtis the coefficient of linear thermal expansion.

For the temperature-dependent material properties,we assume

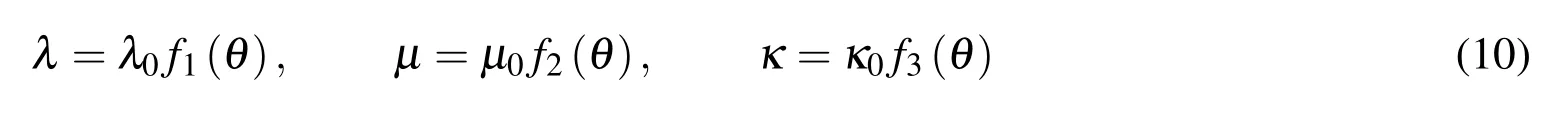
where λ0, µ0and κ0are constants,fi(θ)(i=1,2,3)are given non-dimensional functions of temperature.In case of temperature-independent properties,fi(θ)≡1 and λ = λ0,µ = µ0as well as κ = κ0.Except the properties in(10),the other material properties are assumed to be independent of temperature.

[Rishin,Lyashenko,Akinin and Nadezhdin(1973)]investigated the relationship between modulus of elasticity of several sprayed coatings and temperature,and they reported the modulus of elasticity decreases monotonically with the increasing of temperature.For simplicity and without loss of generality,we assume

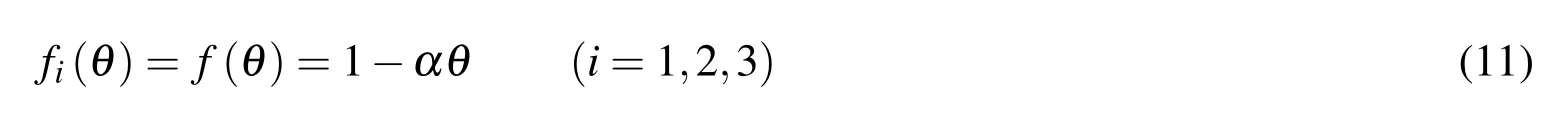
where α is an empirical material constant.

In view of Eqs.(10)and(11),from Eqs.(1)-(6),we can obtain the partial differential governing equations for isotropic thermoelastic problems as

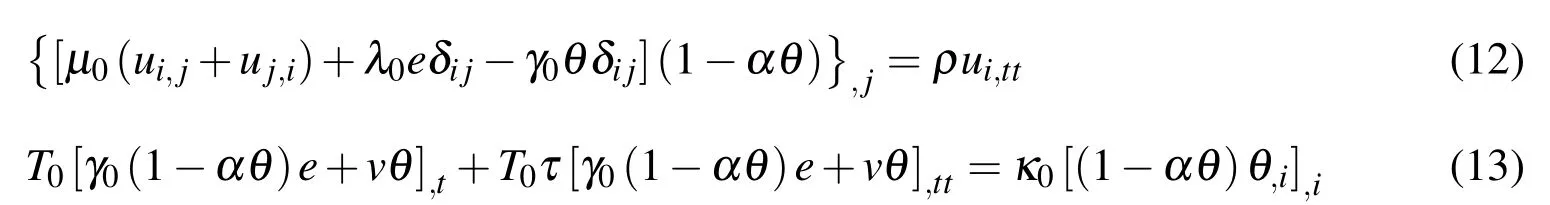
where a comma followed by suffix t denotes the derivative with respect to time.Once α=0,the above equations reduce to the case of temperature-independence of material properties.If the initial conditions and the boundary conditions are given,Eqs.(12)-(13)can be supplemented to solve concrete thermoelastic problems.

Though there are a variety of computational methods as presented by[Dong,Mohiuddine and Atluri(2014)]may be used to solve problems in multidisciplinary engineering and sciences,for the generalized dynamic thermoelastic problems,generally speaking,the integral transform techniques are often adopted to solve such problems.In case of one-dimensional problems,the Laplace transform together with its inverse transform can be used to get the solutions[Sherief and Dhaliwal(1981)],while in case of two-dimensional problems,both Laplace and Fourier transforms and their inverse counterparts have to be employed simultaneously to obtain the solutions[Sherief and Megahed(1999)].Alternatively,the hybrid Laplace transform-finite element method as presented in[Chen and Weng(1988,1989)]can also be used to solve such problems.Unfortunately,as pointed out by[Tian and Shen(2005);Tian,Shen,Chen and He(2006)],the above methods encounter a defect,i.e.,loss of the calculation precision.To overcome such defect,[Tian and Shen(2005);Tian,Shen,Chen and He(2006)]suggested that the generalized dynamic thermoelastic problems could be solved by finite element method and the corresponding finite element equations can be solved in time domain directly.In their work,the obtained results show a higher calculation precision.Nevertheless,for the generalized dynamic thermoelastic problems with temperature-dependent properties,due to the nonlinearity and complexity of the governing equations,it seems a big challenge to get the solutions of such problems by means of the integral transform techniques or the hybrid Laplace transform-finite element method.Fortunately,encouraged by the works of[Tian,Shen,Chen and He(2006);Xiong and Tian(2011a);Xiong and Tian(2011b)],we are about to formulate our problem by finite element method and directly solve the corresponding nonlinear finite element equations in time domain.

3 Finite Element Formulations

To get the finite element equations,we rewrite Eqs.(2)and(3)in vector form as

and the modified Fourier’s law in Eq.(6)as

The considered object can be divided into elements and nodal points and any variable in an element can be approximated by the values of the nodal points of the element together with shape functions.To this end,we introduce two sets of shape functions[Ne1]and{Ne2},and the displacement{u}and the temperature θ on the element level can be expressed respectively as

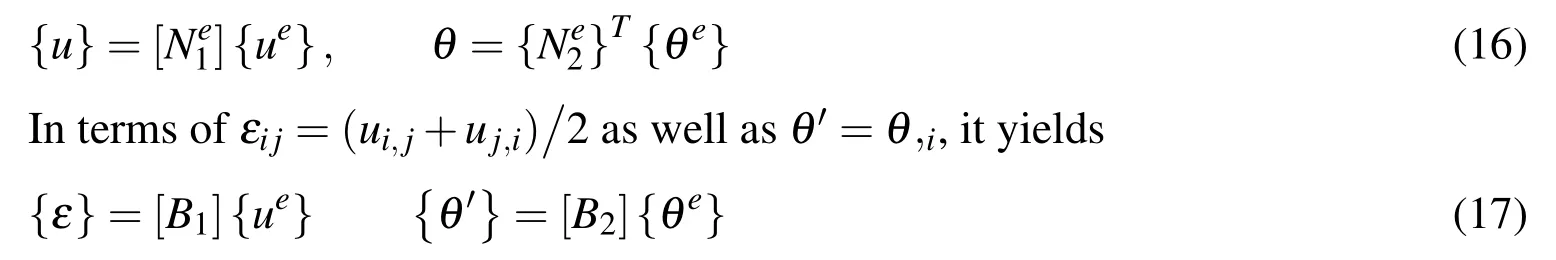
where[B1]and[B2]relate respectively to the first order derivative of component in[]and{}with respect to material coordinates,and they can be explicitly specif i ed once the components of[]and{}are given.The variational form of Eq.(17)is

In the absence of body force,the virtual displacement principle of the generalized thermoelastic problems in the context of L-S theory can be formulated as

where¯Firepresents the components of traction vector,and¯q the heat flux vector.Substituting Eqs.(14)-(18)into Eq.(19),we arrive at

where

Due to the temperature-dependent properties,the matrix of elastic constants[c],the vector of thermal moduli{a}and the matrix of the coefficients of thermal conductivity[κ]are correspondingly temperature-dependent.Thus,the mass matrix,the damping matrix and the stiffness matrix in Eq.(20)are also temperature-dependent,which results in Eq.(20)a nonlinear finite element equation.

To get the solutions in time domain,one of the direct integration methods,the Newmark’s method,labeled as implicit method,is applied to formulating the recursive formula from Eq.(20)for solutions.The considered period S is sub-divided into n intervals of length ∆t=S/n and solution for each timestep ∆t,2∆t,3∆t,...,S is established.Due to the nonlinearity of the mass matrix,the damping matrix and the stiffness matrix in Eq.(20),the set of equations included in the recursive formula is nonlinear.In essence,the problem is materially nonlinear,thus,the modified Newton-Raphson(mNR)iteration method is adopted to obtain the solutions of the system of nonlinear equations at each timestep.In mNR method,the tangential stiffness matrix is formed and decomposed at the beginning of each step and used throughout the iterations,avoiding the formulation of the tangential stiffness matrix as well as its inverse matrix in each iteration step.

4 Numerical Results and Discussions

To demonstrate the above process of solution,we consider a thermoelastic halfspace.The schematic of the considered half-space as well as the applied thermal shock on its bounding surface is shown in Fig.1(a).The bounding surface is assumed to be traction free,and the thermal shock has the following form

where H(·)is the Heaviside unit step function and θ0is a constant.

Assume the half-space is initially at rest,so that,the initial conditions are

Due to the symmetries of geometrical shape and thermal load,the problem can be treated as a plane strain problem and only half of the half-space needs to be considered.The model for simulation is shown in Fig.1(b),where OABC outlines the region for implementing the simulation and OD represents the region within which the thermal shock is applied.The boundary conditions of the problem are

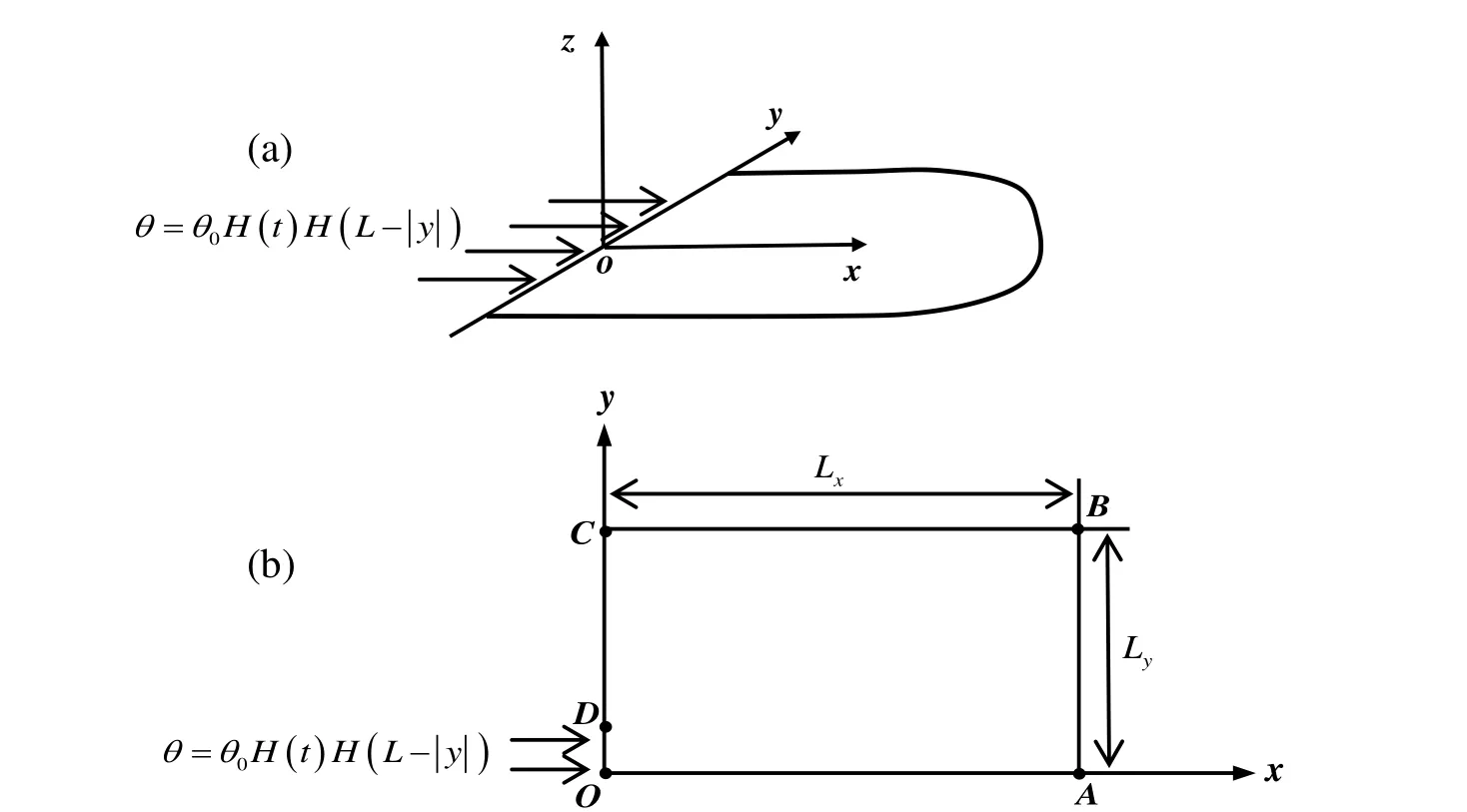
Figure 1:The schematic of the half-space.

assumed to be

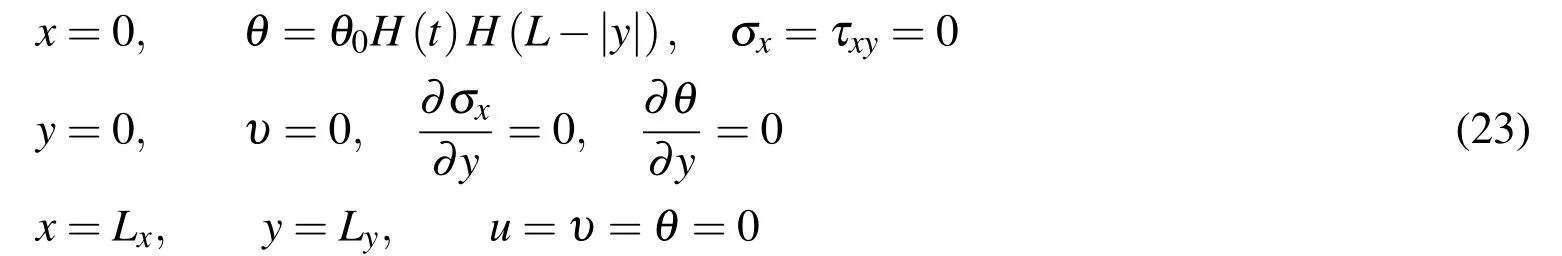
In order to simplify the simulation,the following non-dimensional variables are introduced in the calculation.

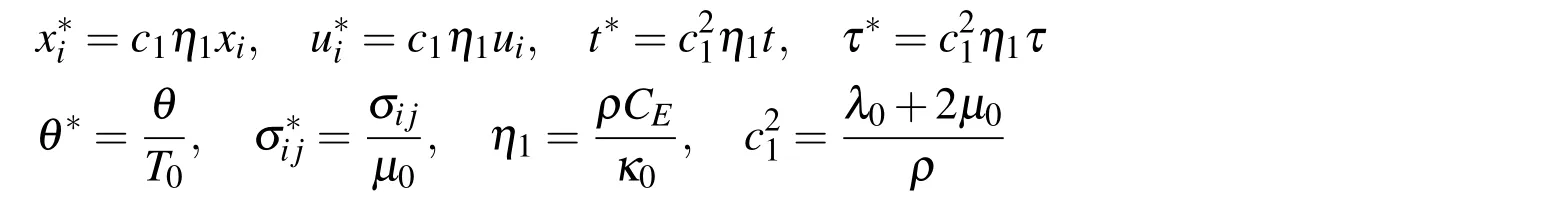
To carry out the simulation,we take τ=0.02,T0=293K,θ0=1,OD=0.2,Lx=2.5 and Ly=3.0.The half-space is taken as copper material and the temperatureindependent material parameters of copper material are given as follows

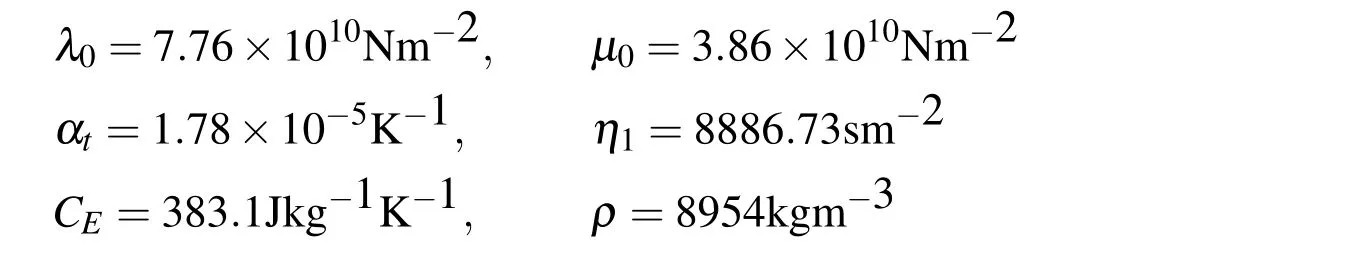
In the calculation,we will reveal how the considered variables change with time tand the temperature-dependent properties.To this end,two values of time(i.e.,t=0.05 and 0.1)and two values of α (i.e.,α =0.0 and 0.002)are considered and four different combinations of t and α are set.Comparisons are made between the results obtained in case of α =0 and those in case of α =0.002.The nondimensional distributions of the considered variables are obtained and illustrated in Figs.2-8 respectively.Fig.2 shows the distributions of the non-dimensional temperature along axis-x.As shown,for the same α,the temperature increases with the increase of time;for the same time,the temperature decreases with the increase of α.At x=0,the value of temperature is 1.0,which is consistent with the amplitude of the applied thermal shock θ0.

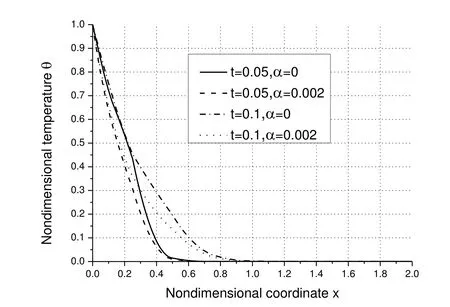
Figure 2: temperature θ along axis-x.

Fig.3 shows the distributions of the non-dimensional temperature along axis-y.As seen,the values of temperature remain constant within y∈[0,0.2],which coincides with the applied thermal shock.Outside y∈[0,0.2],the temperature increases with the increase of time for the same α while decreases with the increase of α for the same time.

Fig.4 shows the distributions of the non-dimensional displacement u along axis-x.Due to the applied thermal shock,the half-space undergoes thermal expansion deformation.As shown,the induced displacement varies continuously from negative to positive till zero,and the negative-positive region transfers dynamically with the passage of time.The magnitude of displacement decreases with the increase of α for the same time while increases with the increase of time for the same α.

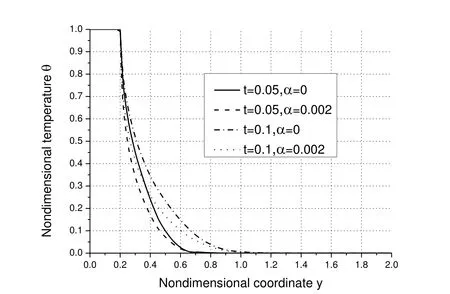
Figure 3:Distributions of the non-dimensional temperature θ along axis-y.

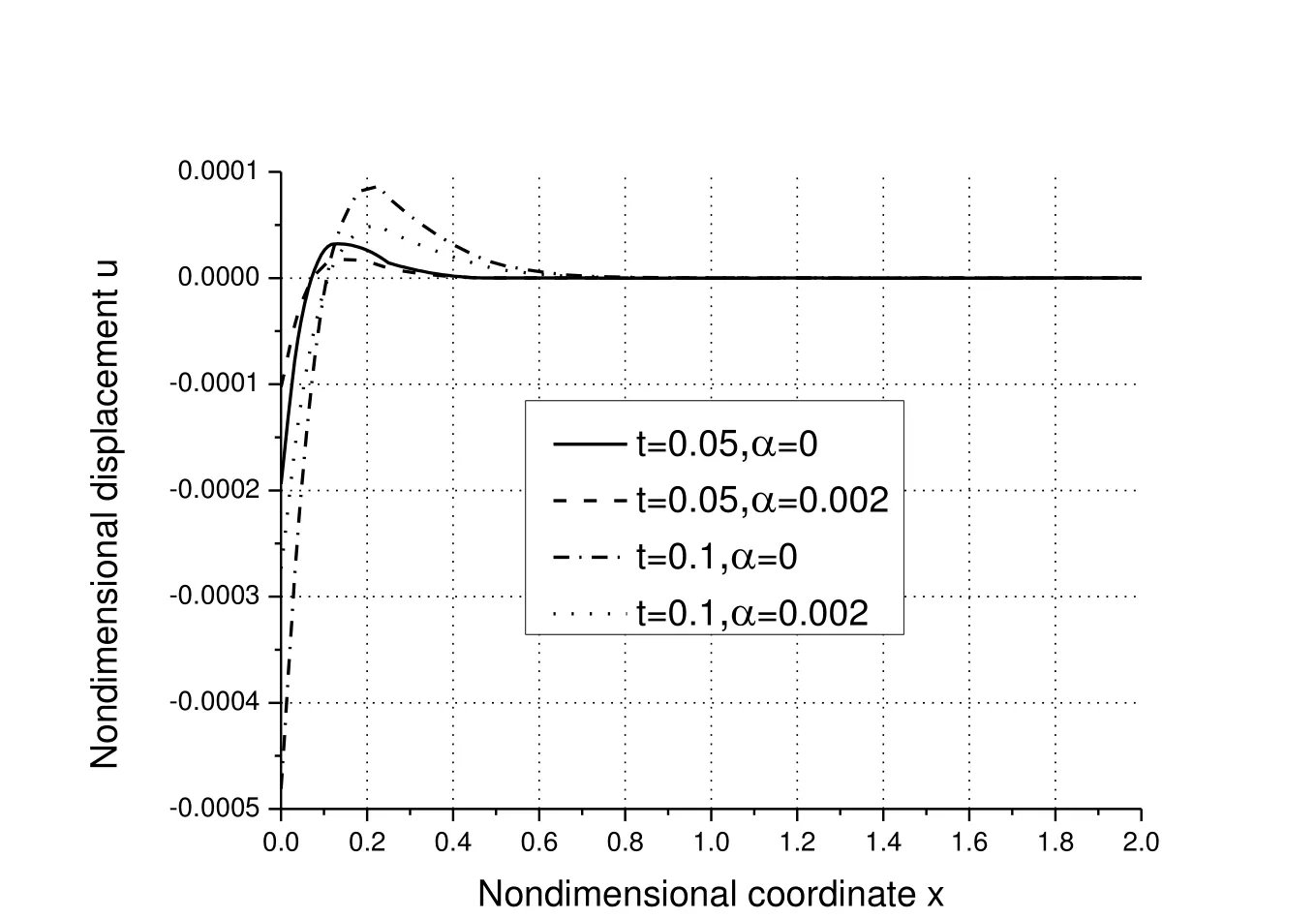
Figure 4:Distributions of the non-dimensional displacement u along axis-x.

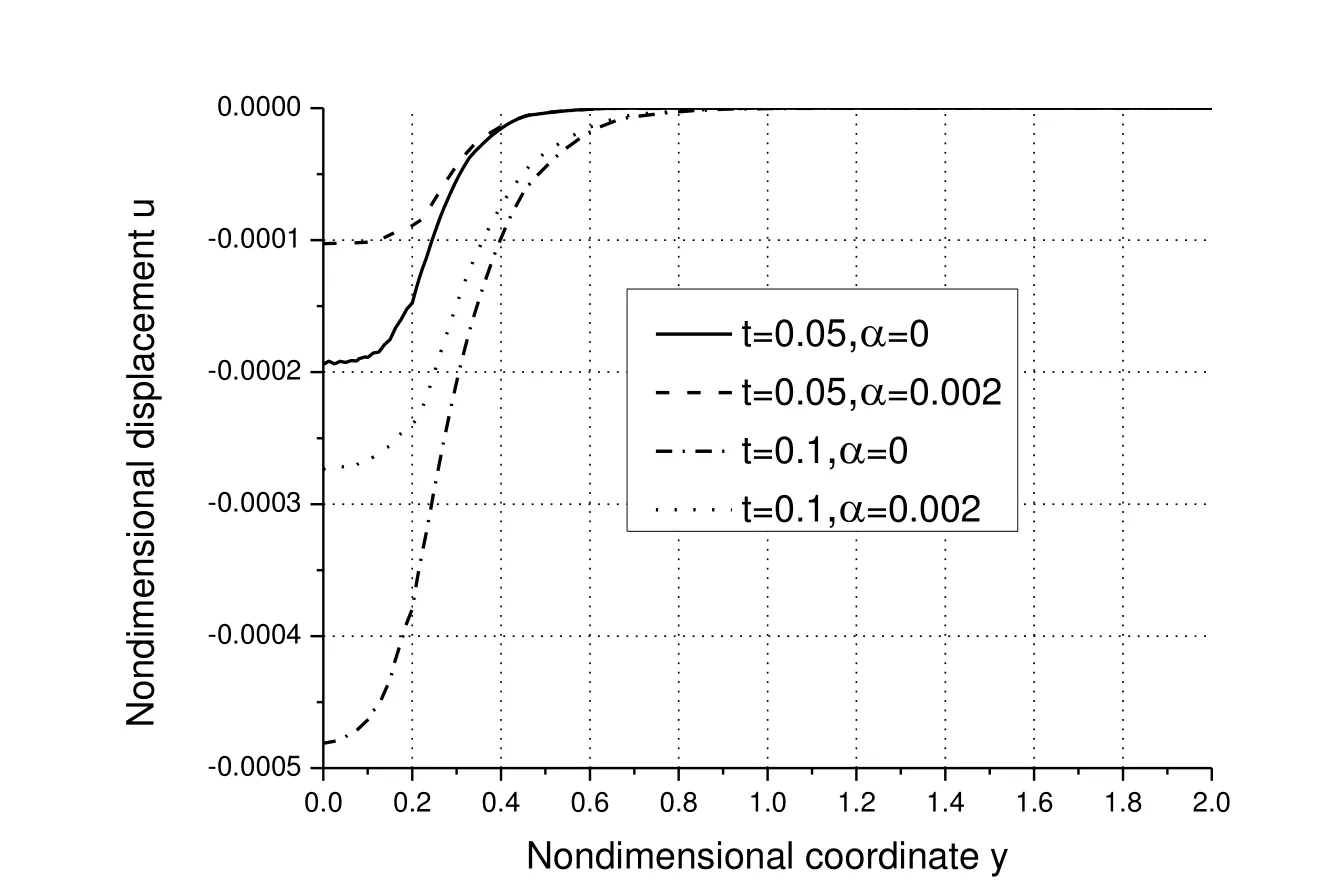
Figure 5:Distributions of the non-dimensional displacement u along axis-y.

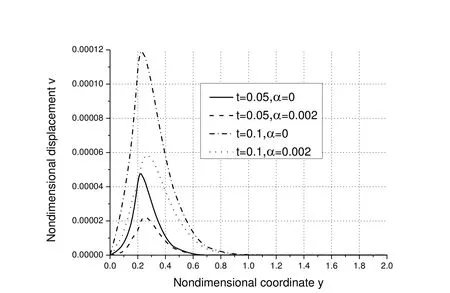
Figure 6:Distributions of the non-dimensional displacement v along axis-y.

Figure 7:Distributions of the non-dimensional stress σxalong axis-x.

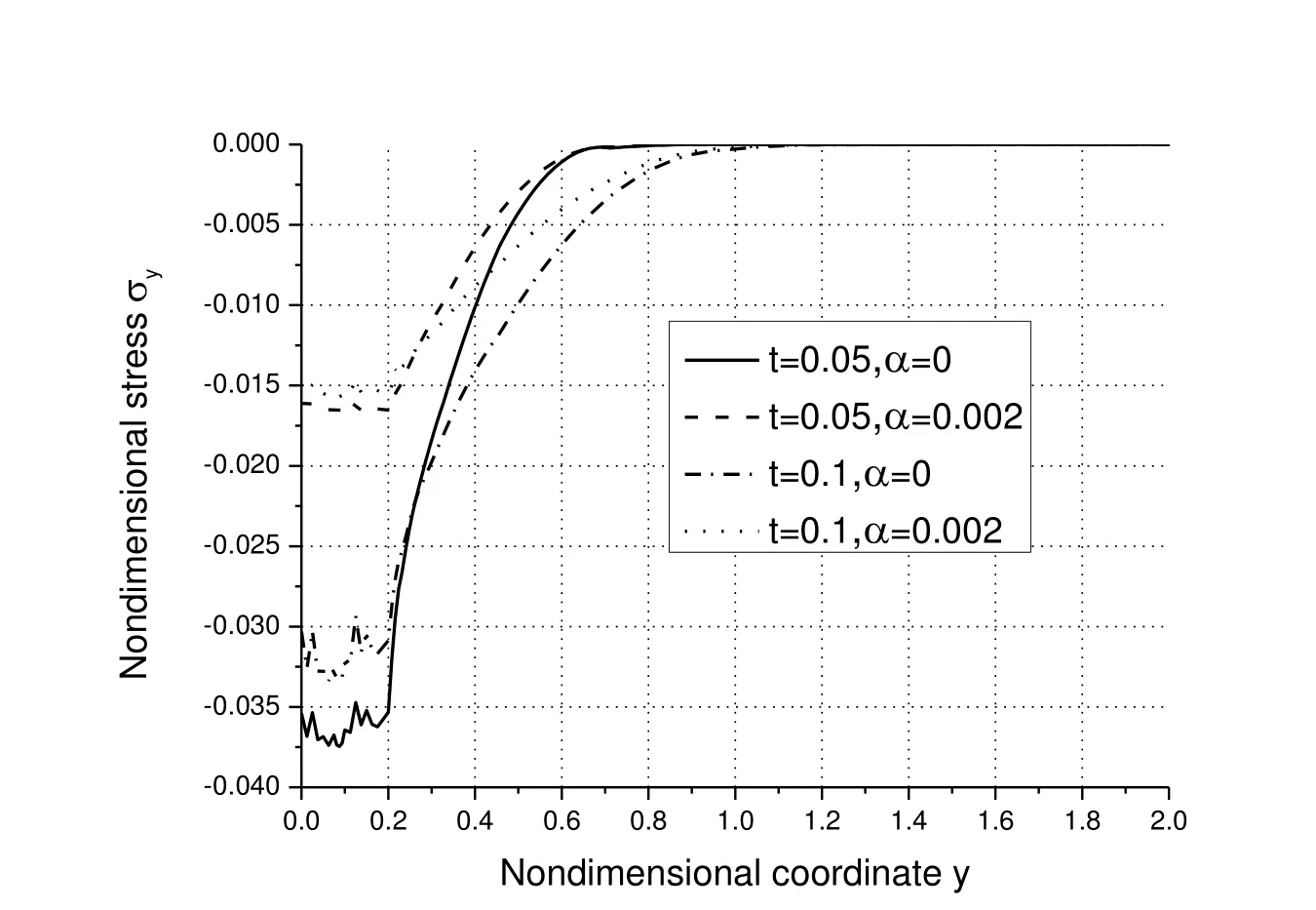
Figure 8:Distributions of the non-dimensional stress σyalong axis-y

Fig.5 shows the distributions of the non-dimensional displacement u along axis-y.As observed,the horizontal displacement along axis-y varies from negative to zero,and the magnitude of the displacement u increases with the increase of time for the same α while decreases with the increase of α for the same time.

Fig.6 shows the distributions of the non-dimensional displacement υ along axis-y.As seen,the magnitude of the vertical displacement along axis-y increases with the increase of time for the same α while decreases with the increase of α for the same time.

Fig.7 shows the distributions of the non-dimensional stress σxalong axis-x.As shown,the non-dimensional stress σxalong axis-x is compressive.With the increase of α ,for the same time the magnitude of σxdecreases.

Fig.8 shows the distributions of the non-dimensional stress σyalong axis-y.As seen,the non-dimensional stress σyalong axis-y is compressive.With the increase of α ,for the same time the magnitude of σydecreases.

From Figs.2-8,it can be found that the non-zero values of all the considered variables are only in a bounded region,which is dominated by the nature that heat wave and thermoelastic wave propagate with finite speeds respectively.

5 Conclusions

The dynamic response of a two-dimensional generalized thermoelastic problem for a half-space with temperature-dependent properties is investigated in the context of L-S generalized thermoelastic theory.The obtained results show that

(1)Due to the finite speeds of heat wave and thermoelastic wave,the non-zero values of all the considered variables are only in a bounded region.

(2)The temperature-dependent properties actually influence the variations of the considered variables and their overall effects act to reduce the magnitudes of the considered variables.

(3)Directly solving the nonlinear finite element equations in time domain is a powerful method to investigate the thermoelastic problems with temperature-dependent properties.

(4)In the investigation of thermoelastic problems,taking the temperature-dependent properties into consideration has practical meaning in the accurate prediction of the thermoelastic behaviors.

Acknowledgement: This work was supported by the National Natural Science

Foundation of China(11372123)and Hong-Liu Excellent Talents Program of Lanzhou University of Technology.

Aouadi,M.(2006):Generalized thermo-piezoelectric problems with temperaturedependent properties.International Journal of Solids and Structures,vol.43,pp.6347-6358.

Aouadi,M.(2007):Hybrid Laplace transform-finite element method to a generalized electromagneto-thermoelastic problem.Applied Mathematical Modeling,vol.31,pp.712-726.

Biot,M.A.(1956):Thermoelasticity and irreversible thermodynamics.Journal of Applied Physics,vol.27,pp.240-253.

Catteneo,C.(1958):A form of heat conduction equation which eliminates the paradox of instantaneous propagation.Compte Rendus,vol.247,pp.431-433.

Chen,T.C.;Weng,C.(1989):Coupled transient thermoelastic response in an axisymmetric circular cylinder by Laplace transform-finite element method.Computer&Structures,vol.33,pp.533-542.

Chen,T.C.;Weng,C.(1988):Generalized coupled transient thermoelastic plane problems by Laplace transform-finite element method.Journal of Applied Mechanics,vol.55,pp.377-382.

Dhaliwal,R.S.;Rokne,J.G.(1989):One-dimensional thermal shock problem with two relaxation times.Journal Thermal Stresses,vol.12,pp.259-279.

Dhaliwal,R.S.;Sherief,H.H.(1980):Generalized thermoelasticity for anisotropic media.Quarterly of Applied Mathematics,vol.38,pp.1-8.

Dong,L.;Alotaibi,A.;Mohiuddine,S.A.;Atluri,S.N.(2014):Computational methods in engineering:a variety of primal&mixed methods,with global&local interpolations,for well-posed or ill-Posed BCs.CMES:Computer Modeling in Engineering&Sciences,vol.99,pp.1-85.

Ezzat,M.A.;El-Karamany,A.S.;Samaan,A.A.(2004):The dependence of the modulus of elasticity on reference temperature in generalized thermoelasticity with thermal relaxation.Applied Mathematics and Computation,vol.147,pp.169-189.

Ezzat,M.A.;Zakaria,M.;Abdel-bary,A.(2004):Generalized thermoelasticity with temperatture dependent modulus of elasticity under three theories.Applied Mathematics and Computation,vol.14,pp.193-212.

Green,A.E.;Lindsany,K.A.(1972):Thermoelasticity.Journal of Elasticity,vol.2,issue 1,pp.1-7.

He,T.H.;Tian,X.G.,Shen,Y.P.(2002):Two-dimensional generalized thermal shock problem of a thick piezoelectric plate of infinite extent.International Journal of Engineering Science,vol.40,pp.2249-2264.

Lord,H.W.;Shulman,Y.(1967):A generalized dynamical theory of thermoelasticity.Journal of the Mechanics and Physics of Solid,vol.15,pp.299-309.

Othman,M.I.A.;Kumar,R.(2009):Reflection of magneto-thermoelastic waves under the effect of temperature-dependent properties in generalized thermoelasticity with four theories.International Communications in Heat and Mass Transfer,vol.36,pp.513-520.

Othman,M.I.A.;Lotfy,K.H.(2009):Two-dimensional problem of generalized magneto-thermoelasticity with temperature-dependent elastic moduli for different theories.Multidisciplinary Modeling in Materials and Structures,vol.5,pp.235-242.

Othman,M.I.A.;Song,Y.Q.(2008):Ref l ection of magneto-thermoelasticity waves with two relaxation times and temperature-dependent elastic moduli.Applied Mathematical Modeling,vol.32,pp.483-500.

Rishin,V.V.;Lyashenko,B.A.;Akinin,K.G.;Nadezhdin,G.N.(1973):Temperature dependence of adhesion strength and elasticity of some heat-resistant coatings.Strength of Materials,vol.5,pp.123-126.

Sherief,H.H.;Anwar,M.N.(1994):State-space approach to two-dimensional thermoelasticity problems.Journal of Thermal Stresses,vol.17,pp.567-590.

Sherief,H.H.;Dhaliwal,R.S.(1981):Generalized one-dimensional thermal shock problem for small times.Journal of Thermal Stresses,vol.4,pp.407-420.

Sherief,H.H.;Megahed,F.A.(1999):A two-dimensional thermoelasticity problem for a half space subjected to heat sources.International Journal of Solids and Structures,vol.36,pp.1369-1382.

Tian,X.G.;Shen,Y.P.;Chen,C.Q.;He T.H.(2006):A direct finite element method study of generalized thermoelastic problems.International Journal of Solids and Structures,vol.43,pp.2050-2063.

Tian,X.G.;Shen,Y.P.(2005):Study on generalized magneto-thermoelastic problems by FEM in time domain.Acta Mechanica Sinica,vol.21,pp.380-387.

Vernotte,P.(1961):Some possible complications in the phenomenon of thermal conduction.Compte Rendus,vol.252,pp.2190-2191.

Xiong,Q.L.;Tian X.G.(2011a):Response of a semi-infinite microstretch homogeneous isotropic body under thermal shock.Journal of Applied Mechanics,Transactions ASME,vol.78,044503.

Xiong,Q.L.;Tian,X.G.(2011b):Transient magneto-thermoelastic response for a semi-infinite body with voids and variable material properties during thermal shock.International Journal of Applied Mechanics,vol.3,pp.881-902.

1Corresponding author.E-mail:heth@lut.cn

2Key Laboratory of Disaster Prevention and Mitigation in Civil Engineering of Gansu Province,Lanzhou University of Technology,Lanzhou 730050,P.R.China.

3School of Science,Lanzhou University of Technology,Lanzhou 730050,P.R.China.