三角高程网严密平差全新方法的研究

达乾龙，刘成龙，何林烜，杨雪峰

(西南交通大学地球科学与环境工程学院，四川成都611756)

一、引 言

在高程控制测量中，常用的测量方法有水准测量和三角高程测量。水准测量具有操作简单、测量精度高等优点，但视距短、测量效率低，且易受到地形的限制，适用于开阔平坦地区的高程控制网测量［1］。三角高程测量相较于水准测量具有测量效率高、不受地形起伏限制、单站测距长，以及跨越江河、峡谷水准测量无法到达的目标点等优点，已经广泛应用于工程测量和大地测量中。

三角高程测量中的原始观测值是全站仪中心到棱镜中心的斜距和天顶距，其观测质量直接影响到三角高程网的可靠程度。三角高程测量精度主要受大气折光和地球曲率［2］的影响，为消除和减弱它们对测量结果的影响，需要进行往返测量，在精密工程测量中常采用同时对向观测［3］的三角高程测量方法。在对三角高程网平差计算时，传统的做法是根据原始观测值计算测站点到目标点的三角高差和水平距离，以三角高差为观测值，以水平距离的倒数定权进行间接平差［4］。可以看出，传统的三角高程网平差方法和水准测量平差方法类似，即利用测段的三角高差和测段长度进行平差计算。这种平差方法简单易于理解，但在理论上是有缺陷的，因为斜距和天顶距才是三角高程测量的原始观测值，而三角高差是通过斜距和天顶距计算得到的，根据间接平差原理，应该对原始观测值开列误差方程并进行后续的平差计算和精度评定。因此，本文针对传统三角高程网平差存在的问题，提出了三角高程网严密平差的全新方法，新平差方法的误差方程以观测的斜距和天顶距作为观测值，以控制点的高程作为未知参数，得到线性化的误差方程，然后进行后续的平差计算。

新平差方法不仅可以计算控制点的高程平差值和高程中误差，还可以计算斜距和天顶距的改正数及其中误差。

二、斜距和天顶距的误差方程式开列及权的确定

图1为三角高程测量原理［5］示意图，A、B为地面上的两个高程控制点，在A点架设全站仪，在B点设置觇标，测得斜距SAB和天顶距aAB，同时测得仪器高iA和觇标高jB，则A、B间的高差hAB的计算公式为

根据三角高程测量的原理，本文提出的三角高程网严密平差的全新方法以控制点高程作为未知参数，将天顶距、斜距作为观测值开列误差方程，以仪器标称精度定权，然后再利用最小二乘原理进行平差计算。由于三角高程测量的观测值中包含天顶距和斜距两种类型，因此构建误差方程的思路为:首先将天顶距视为真值，将斜距作为观测值开列斜距的误差方程;然后再将斜距视为真值，将天顶距作为观测值开列天顶距的误差方程。对建立的两类观测值误差方程再进行联合平差，就可以得到控制点的高程平差值及其中误差、观测值斜距和天顶距的改正数及其中误差。

图1 三角高程测量原理

1.斜距误差方程开列

斜距误差方程开列的思想是:以控制点高程作为未知参数，将天顶距视为真值，把斜距作为观测值建立斜距的误差方程。由式(1)可知

式(5)中方程右端项分母不再趋近于0，其病态问题得到了解决，将式(5)写为误差方程的形式

式(7)即为将天顶距视为真值、斜距为观测值时的斜距误差方程。

2.天顶距误差方程开列

天顶距误差方程开列的思想是:以控制点高程作为未知参数，将斜距视为真值，把天顶距作为观测值建立天顶距的误差方程。由式(1)知

常数ρ=206 265，式(9)即为将斜距视为真值、天顶距作为观测值时的天顶距误差方程。式(7)和式(9)共同组成三角高程网严密平差全新方法的误差方程。

3.观测值权的确定

新方法中观测值的权采用验前估计法［7］确定，即根据仪器的标称精度定权。设天顶距测量中误差为ma，ma常取值为方向观测中误差的倍，其权为Pa;斜距测量中误差为mS，其权为PS。σ0为单位权中误差，令 σ0=ma，则观测值 aAB和 SAB的权［8］分别为

式中，斜距中误差mS按全站仪测距标称精度计算，即 mS=a+b×S 或和 b分别为全站仪测距的固定和比例误差。

三、平差及其精度评定

根据式(7)和式(9)可得到三角高程网严密平差全新方法误差方程［4］的矩阵形式为

采用以上定权方式可得观测值权矩阵为P，按最小二乘原理可解算出未知参数改正数向量为

将式(12)的结果代入式(11)求出V，再按下式可求出平差后观测值单位权中误差为

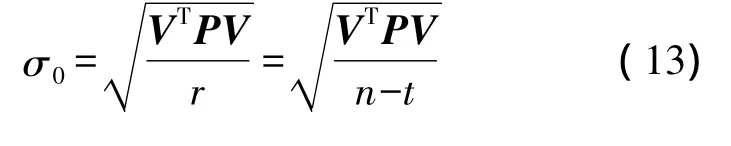
式中，n为观测值个数;t为必要观测值个数，即三角高程中未知高程点的个数。根据间接平差原理和协因数传播定律可得，未知参数协因数矩阵为Q^X=(BTPB)－1，观测值改正数的协因数矩阵为QVV=QB(BTPB)－1BT，其中Q=1/P。则控制点的高程中误差和观测值改正数(斜距、天顶距)的中误差计算公式分别为

四、试验验证与分析

为验证三角高程网平差新方法的正确性和合理性，本文进行了测量与平差计算试验。

1.试验概况及平差计算

在三角高程控制网建立过程中，为验证该平差方法对地形起伏较大和地形平坦的控制网是否均适用，建立了如图2所示的控制网。网中各边边长均已标于图中，其中A点与其他点的高差约为5～6 m，B、C、D、E点间高差约为0～2 m。对该网分别进行了三角高程测量和水准测量，三角高程测量中采用徕卡TCRA 1201全站仪(标称精度:方向测量中误差为1″，测距中误差为1 mm+1×10－6D)进行对向观测，在每一控制点上架设仪器，测量该点到其余4个点的天顶距和斜距，同时量取仪器高和棱镜高;水准测量中采用的水准仪是天宝DiNi03，按国家二等水准测量的技术要求进行。

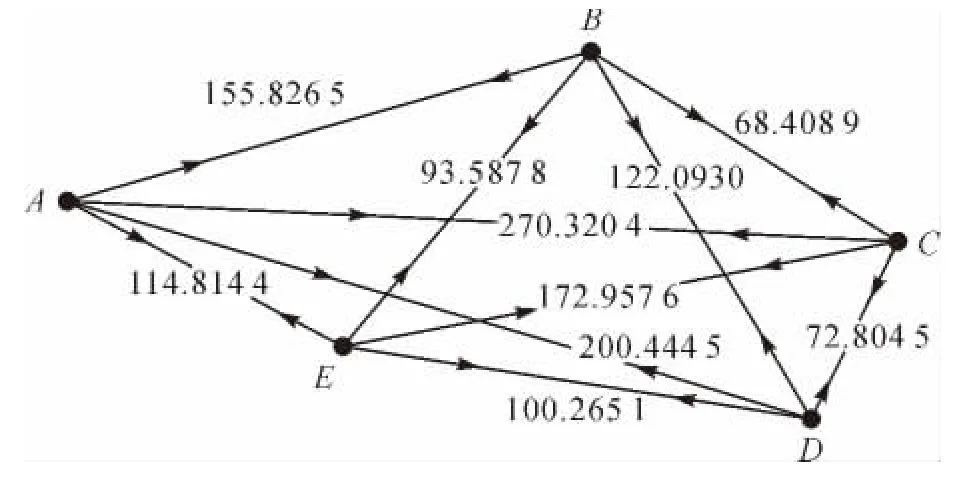
图2 试验网网形示意图(边长单位:m)

取得合格的三角高程网测量及水准测量的外业数据后，分别采用传统三角高程网平差方法、本文提出的三角高程网平差新方法及水准测量平差方法进行平差。平差时，以控制点D点为基准高程点，高程值为 50.000 m，A、B、C、E 为未知高程点。采用全新的三角高程网严密平差方法进行平差，得到控制点高程及其中误差，观测值改正数及其中误差。其中表1给出了新方法平差后部分观测值的改正数及中误差。采用传统三角高程网平差方法进行平差，得到控制点高程平差值及其中误差、控制点间高差改正数及其中误差。采用水准测量方法平差，得到控制点高程平差值及其中误差、控制点间高差改正数及其中误差。

表1 新方法平差观测值的改正数及中误差

2.平差结果的对比与分析

(1)3种平差结果对比与分析

对于该高程控制网采用3种平差方法得到同一个高程点的3种高程平差值，表2给出了不同方法的高程平差结果和相互间的高程较差。

表2 不同方法的高程平差结果和同名点高程较差

从表2可以看出，对三角高程网采用全新平差方法与传统平差方法得到的同一点高程平差值进行比较，最大差值为0.2 mm，说明新方法能得到正确的高程平差值，满足内符合精度;另外，两种三角高网平差与水准测量平差得到的同名控制点高程较差在1 mm左右，满足外符合精度。存在差异主要是由仪器高和目标高的量取误差所造成的，若采用强制对中装置，则可避免这两种量取误差，使得三角高程网平差结果与水准测量平差结果差异更小。

(2)利用观测值平差值计算控制网高程闭合差

采用全新的三角高程网平差能够得到观测值(斜距和天顶距)的平差值，为验证观测值平差结果是否合理，利用观测值平差值反算了各控制点间的高差，组成了多个高程网闭合环，并统计平差前后高程网的高差环闭合差，部分高程网高差环闭合差见表3。

表3 高程网高差环闭合差 mm

通过表3平差前后高差环闭合差的对比可看出，平差前各环闭合差的绝对值在0.10～1.00 mm范围内，平差后各环闭合差的绝对值均小于0.05 mm，可见平差后较平差前小了一个数量级。理论上平差后各高差环闭合差应该为零，本次试验中仍有小于0.05 mm的闭合差，主要是由于平差过程中的近似和计算取整误差造成的。

通过表2和表3的试验结果及其比较，可以证明本文提出的三角高程网严密平差新方法的平差结果是正确和可靠的。

五、结 论

1)通过全新三角高程网平差和传统三角高程网平差结果的比较，可发现两种方法的高程平差值很接近，说明本文提出的三角高程网平差新方法能得到正确的高程值及其中误差。

2)采用全新三角高程网平差方法可以对观测值进行精度评定，可以直观地反映外业观测质量的好坏，这对于测量人员来说是非常重要的，方便观测值质量的检查或补测超限的观测值。

3)本文研究结果表明，三角高程网严密平差的全新方法比传统的三角高程网平差方法更为严谨和合理。

［1］中华人民共和国铁道部.TB 10601—2009高速铁路工程测量规范［S］.北京:中国铁道出版社，2009.

［2］郭宗河，郑进凤.电磁波测距三角高程测量公式误差的研究［J］.测绘通报，2004(7):12-13.

［3］刘成龙，杨雪峰，张阅川.基于测量机器人的二等高程控制测量新方法［J］.西南交通大学学报，2013，48(1):69-74.

［4］武汉大学测绘学院测量平差学科组.误差理论与测量平差基础［M］.武汉:武汉大学出版社，2003.

［5］张正禄.工程测量学［M］.武汉:武汉大学出版社，2005.

［6］张俊，文鸿雁，刘立龙.大地测量中法方程病态性问题的初探［J］.海洋测绘，2006，26(5):1-3.

［7］龚率.工程控制网平差的定权方法研究及其软件研制［D］.成都:西南交通大学，2013.

［8］崔希璋，於宗俦，陶本藻，等.广义测量平差［M］.2版.武汉:武汉大学出版社，2001.

［9］徐士良.数值分析与算法［M］.机械工业出版社，2003.

［10］肖根旺，许提多，周文健，等.高精度三角高程测量的严密公式［J］.测绘通报，2004(10):15-17.

［11］倪先桃.无砟轨道CPⅢ高程控制网测量与数据处理方法研究［D］.成都:西南交通大学，2009.

［12］郑汉球.光电测距三角高程和重力水准面曲率不等差改正［J］.测绘学报，1991，20(4):260-268.