列联表的两种抽样模型以及齐性和独立性的检验问题

禹建奇

摘要：本文讨论二维列联表数据的两种抽样模型，以及相关的齐性和独立性检验问题，说明两种抽样模型的联系，以及齐性及独立性检验的一致性.

关键词：列联表；抽样模型；齐性；独立性检验

中图分类号：G642.0 文献标志码：A 文章编号：1674-9324（2015）14-0071-02

作者在讲授统计课程时，经常会遇到列联表的齐性和独立性检验问题，这两个问题分别牵涉到两种抽样方式，但两种检验的检验统计量与结果却是一样的.大多数教材，如吴喜之、赵博娟所著《非参数统计》，只是简单指出两种抽样方式的不同，两种检验的一致性只是殊途同归，巧合而已.本文论证了这两种模型的联系，导出两种检验的一致性，可见，这种一致性绝不是巧合.

一、乘积多项分布模型与整体多项分布模型

首先我们来看两个二位列联表的例子（摘自吴喜之、赵博娟所著《非参数统计》第八章）.

例1 对于某种疾病有三种处理方法，某医疗机构分别对22，15和19个病人用这三种方法处理，处理的结果分“改善”和“没有改善”两种，并且列在下表中：

问：不同处理的改善比例是不是一样？

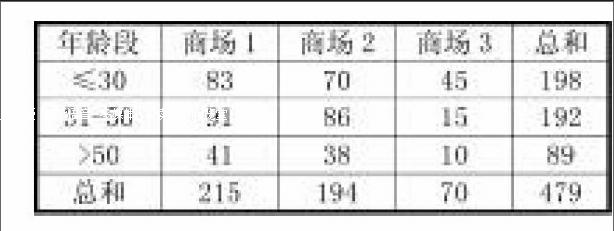
例2 在一个有三个主要百货商场的商贸中心，调查者问479个不同年龄段的人首先去三个商场中的哪一个，结果如下：

问：人们对这三个商场的选择和他们的年龄是否独立？

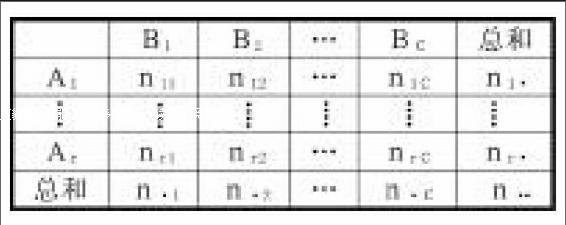
这两个例子的数据都有下面的两因子列联表形式：

这里，每个格子的频数nij为随机变量，行频数总和ni？誗=∑jnij，列频数总和n？誗j=∑inij，频数总和n？誗？誗=∑ini？誗=∑jn？誗j，A1，A2，…，Ar为行因子的r个水平，B1，B2，…，Bc为列因子的c个水平.用pij表示第ij个格子频数占总频数的理论比例（概率）.显然，pij=E（nij）/n？誗？誗，这里E（nij）为nij的数学期望，而相应的第i行的理论比例（概率）pi？誗及第j列的理论比例（概率）p？誗j分别为pi？誗=∑jpij，p？誗j=∑ipij？誗

对于例1的具体问题，零假设为：“对于各种不同的处理，改善的比例或概率相同.”注意，这里因为只有两种结果，所以，对不同处理改善的比例相同就意味着对各种处理没有改善的比例也相同.这种关于齐性的检验的数据获取，一般都类似于例8.1，对行变量的每一水平i，试验前选定一定数目（ni·）的对象，然后在试验时观测并记录在列变量的不同水平所得到的相应频数.

可以看到，这和前面检验齐性时零假设下的期望值一样，由此可以得到和上面检验齐性时导出的同样的统计量Q，这样导出的Q当然也有同样的渐近 χ2分布.这类关于独立性的问题的数据获取，通常是随机选取一定数目的样本，然后记录这些个体分配到各个格子的数目（频数）.它并不事先固定某变量各水平的观测对象数目，这和齐性问题有所区别.

一般地，对r×c的列联表，试验前先选定总频数n？誗？誗，再进行独立抽样，记录n？誗？誗个对象落在各个格子的频数，这样，整个列联表的分布为一多项分布

这种抽样模型称列联表的整体多项分布模型.

二、两种模型的联系

如上所述，很多的统计教材也都指出，同一个列联表数据可以有两种抽样模型，而且对两种模型分别做齐性和独立性检验时，检验过程与结论完全一样，但是其中的缘由却未见说明.其实可以证明，这并不是巧合， 它是下面两个定理的结果.

定理一：齐性问题与独立性问题等价， 即各行的齐性等价于行与列变量的独立性.

三、最后结论

整体抽样模型的独立性当然等价于固定各行总频数时的齐性，所以，综合可得以下结论：

二维列联表的数据，可能来自两种不同的抽样模型： 整体多项分布模型和乘积多项分布模型， 但是两种模型其实是一致的， 即乘积多项分布模型可以认为是整体多项分布模型在限定各行总频数的条件下的条件分布模型， 同时由于齐性与独立性的等价， 不论以何种模型分析同一个列联表的齐性或独立性，得到的结果是一样的.

参考文献：

[1]吴喜之，赵博娟.非参数统计[M].中国统计出版社，2013.

[2]阿兰，阿格莱斯蒂.分类数据分析[M].重庆大学出版，2012.