激光制导炸弹的姿态控制引入时机研究*

王 颖，赵艳辉，张拥军

(中国空空导弹研究院，河南洛阳 471000)

0 引言

外挂导弹投放时和载机的分离安全问题一直备受关注，所谓安全分离是指导弹在飞离载机的过程中载机、发射装置和其他武器不产生损坏、碰撞或有害的影响。

错开载机距离的能力是衡量外挂导弹能否安全分离的重要指标此错开距离是弹道初段外挂物任一部分同载机之间的最小距离，通常垂直距离比水平距离要大，一般垂直距离大于7～10个弹体直径可认为弹体离开了对载机的危险区。在危险区内对导弹进行有效控制就尤为重要，如果起控时间早，导弹机动时可能会碰到载机，如果起控时间晚，会影响导弹的发射性能，因此控制时机的选择就变得更为重要。

文中所介绍的是小型激光制导炸弹从载机的安全分离问题，该型导弹是挂装在无人机等轻型飞机上的，主要靠重力脱离载机，并且在小攻角下是静不稳定的。为了实现导弹的安全分离，需要在分离瞬间控制4个舵面保持零位。在满足一定安全距离后，适时让稳定回路引入姿态控制，促使舵面偏转实现对弹体姿态变化的抑制，确保离开载机过程中弹体的姿态稳定，防止姿态变化过快而使控制系统发散。

1 数学模型

1.1 弹体物理参数

弹体主要物理参数包括特征长度、特征面积、3个轴向的转动惯量、质量和质心位置等。

1.2 气动系数建模

1.2.1 气动模型

将弹体气动模型建立在执行坐标系上，气动系数计算完成后，通过坐标变换转换为弹体坐标系中的气动系数。弹体系和测量系指向一致，执行系单独定义，如图1所示。

执行坐标系指向和舵翼面伸展方向一致，和弹体系相差45°度。惯性测量信息转换到执行系送给稳定回路进行反馈控制。导航所用的惯性测量信息不需要转换。

舵面分解方式为:

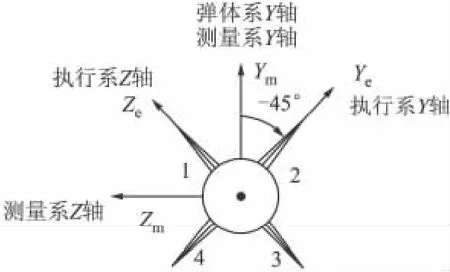
图1 弹体系、测量系和执行系定义

式中 δr、δp、δy分别为三通道舵控，δ1、δ2、δ3、δ4分别为分解到舵面上的控制指令。

1.2.2 坐标系转换

惯性测量量要转换到弹体执行系下，送给控制回路进行反馈控制;弹体模型计算攻角和气流扭角时要增加一次转换，将弹体系中的速度分量转换到执行系;气动力系数和气动力矩系数要从弹体执行系转换到弹体系，之后通过动力学运算得到惯性测量量，送惯测模型。

测量系和弹体系重合，弹体执行系和弹体系的转换矩阵如式(3)和式(4)所示，下标m为测量系，下标e为执行系。

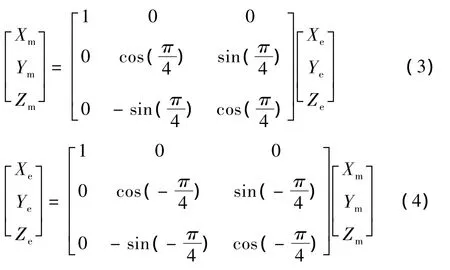
1.3 弹体动力学模型

1.3.1 弹体坐标系气动力和气动力矩模型

弹体气动力和气动力矩模型如下所示［1］:

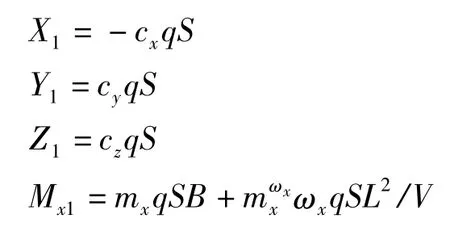
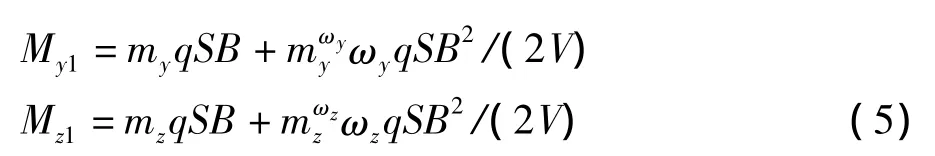
1.3.2 弹体坐标系质心平动动力学方程

弹体质心平动动力学方程如下所示［1］:

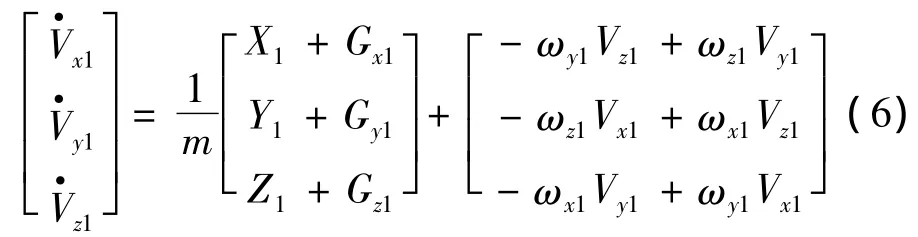
1.3.3 弹体坐标系绕质心转动的动力学方程

弹体绕质心转动的动力学方程如下所示［1］:

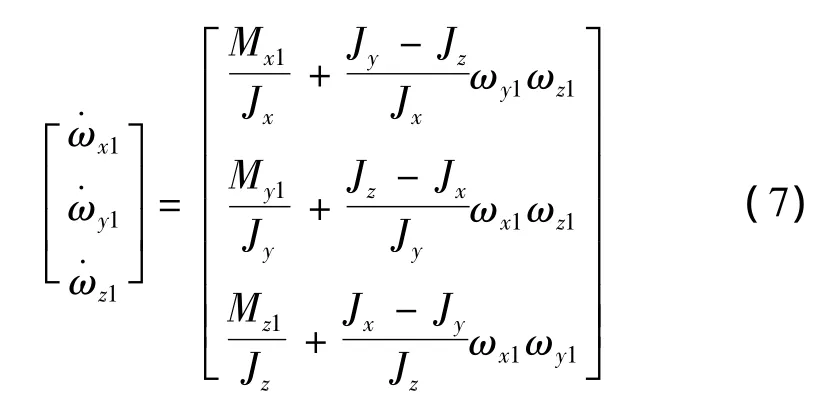
2 起控时间参数对载机安全影响

来自载机周围的气流扰动对导弹姿态有影响，进而又对载机安全造成影响。为实现机弹的安全分离，主要采取在导弹无控段合适的时间点介入稳定回路，控制弹体姿态稳定，在不满足起控条件时进行零指令控制，这样既能保证载机安全又能保证导弹性能。

稳定回路姿态控制引入时机的选取对发射安全和导弹性能都会有影响。如果引入时机较早，弹体机动时可能与飞机碰撞，危及载机安全;如果引入时机较晚，则会影响导弹性能，还可能会使导弹没有足够的时间修正初始积累误差或者需要很大的控制力才能将导弹的姿态稳定下来。对于没有发动机的激光制导炸弹而言，当积累的角度和角速度误差较大情况下，稳定回路开始工作时需要纠正的系统误差较大，容易造成控制量饱和，所以评估和分析接通稳定回路的时间点尤为重要，在合适的时机抑制弹体姿态大幅变化，不但有利于和载机的分离安全，还能节省为纠正系统较大姿态误差的使用能量。

3 数字仿真分析

针对激光制导炸弹在机弹分离后稳定回路姿态控制不同引入时机进行数字仿真分析，通过算例数据的对比分析得出该激光制导炸弹姿态控制引入的最佳时机。

算例选取目标点为坐标原点，机弹分离时弹道和目标的水平距离为3 000 m、相对高度为3 000 m、初始速度为180 m/s、偏航方向为－90°。

图2给出了导弹在典型条件下物理分离后0～1s、间隔0.1s时不同时机引入姿态控制的舵控曲线，其中 δ0～ δ3分别为 4 个舵面上的舵控，δr、δp、δy分别为三通道舵控。

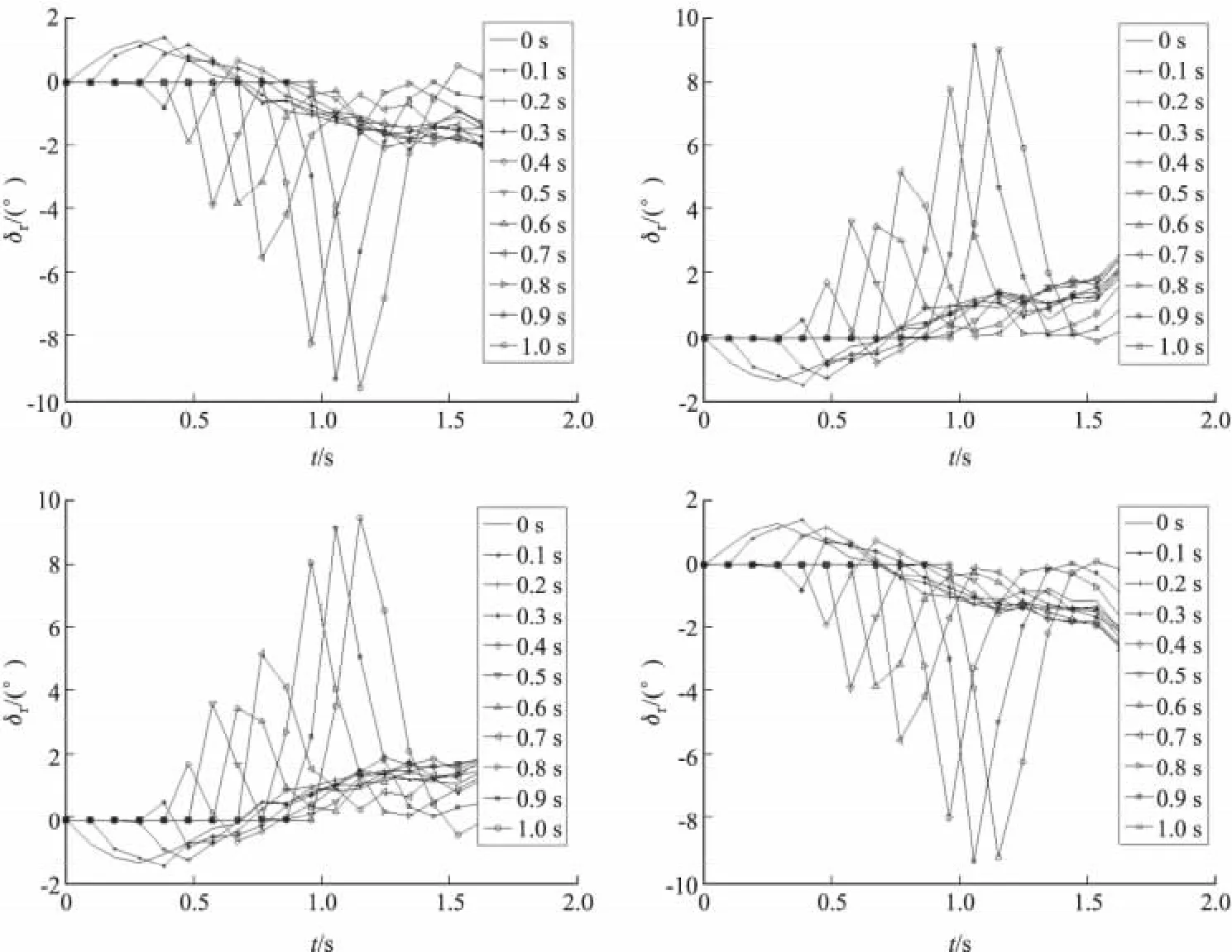
图2 1s内姿态控制引入的舵控曲线

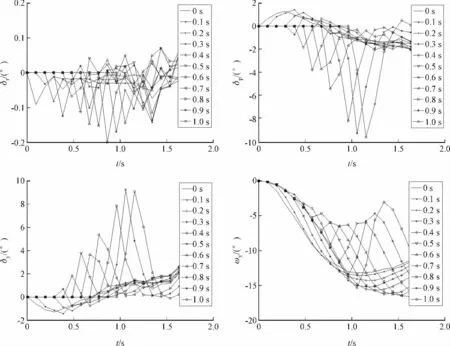
图3 1s内姿态控制引入的三通道舵控曲线

通过图2、图3可以得出，在离机0.3 s时舵面控制幅度最小，即此时引入对弹体的姿态控制能够在最小的舵偏下达到弹体姿态的稳定。下面列出无控条件和离机0.3 s引入姿态控制的弹体姿态曲线和位置变化曲线。

由图4可看出，在低空低速飞行状态下，加入控制0.3 s内导弹位置的变化与无控状态相差不大，弹体在y方向位移变化相对较大，在重力作用下离机0.3 s时y向位移约0.45 m，远大于根据此时弹体姿态计算得到的导弹离机最小距离，处于安全分离状态。

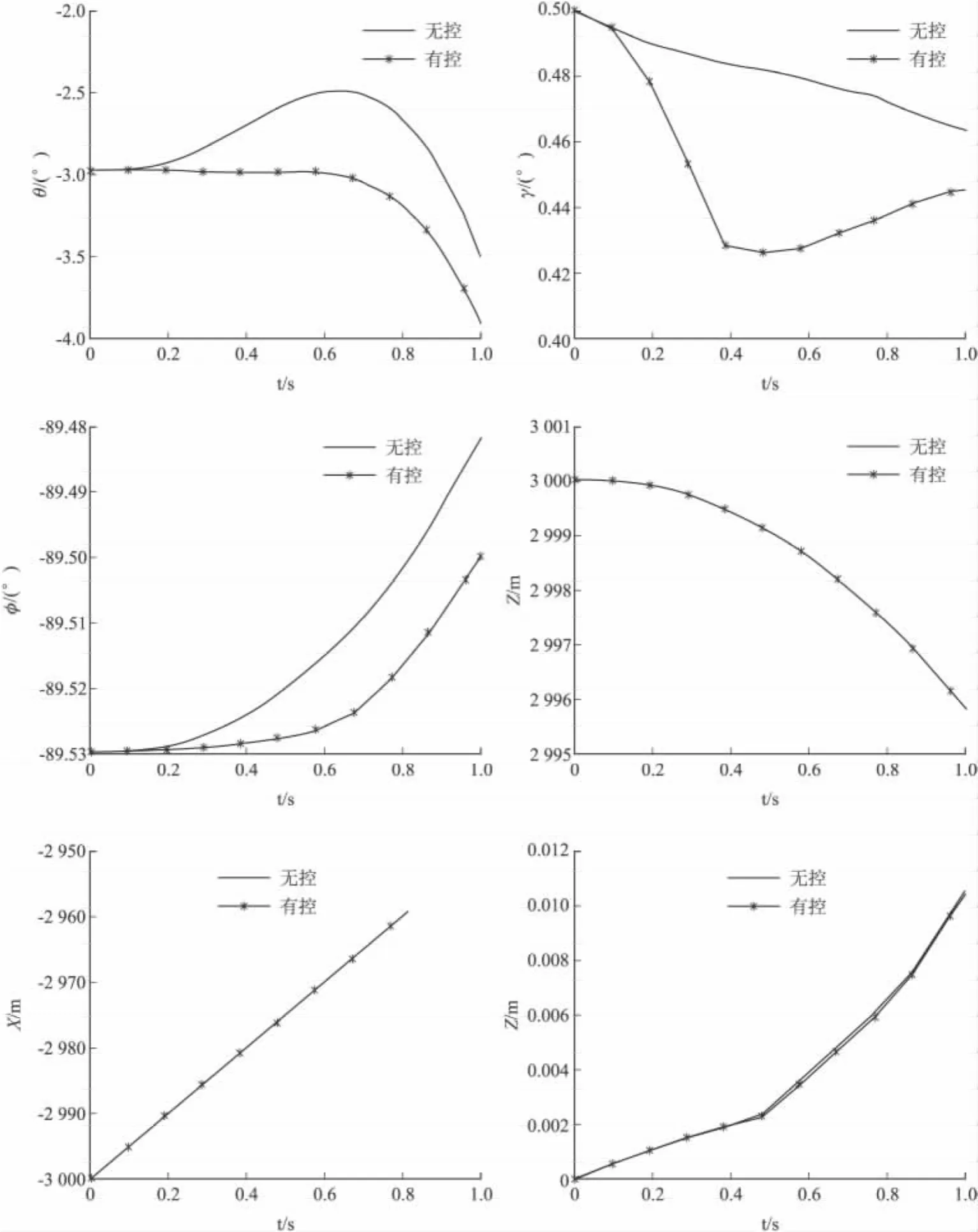
图4 1s内姿态和位置变化曲线

而对于弹体姿态相对于无控的变化比较明显，姿态控制的引入明显减小了姿态误差的变大趋势，特别是俯仰角的增大趋势受到抑制，滚转角向零靠近趋势增大，使弹体姿态得到有效控制，弹体稳定可控，不会威胁载机安全。

4 结论

文中针对小型激光制导炸弹从载机的安全分离问题，提出了在适当时机引入稳定回路姿态控制，驱动舵面偏转实现对弹体姿态变化的抑制，确保了导弹离开载机过程中的姿态稳定，证明了起控时间参数计算的合理性。

通过算例仿真和无控条件下机弹分离后弹体姿态变化的对比分析，验证了在仿真计算得到的起控时机引入姿态控制，有利于弹体姿态稳定，还可以避免出现控制量饱和，有效防止了控制系统发散。同时，也拉大了与制导回路开始作用时的时间间隔，有助于使弹体在开始响应制导指令时处于较平稳的状态。

因此，文中所介绍的在适当时机采取姿态控制有利于导弹的姿态稳定，保证了导弹投放时的载机安全。

［1］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京:北京理工大学出版社，2000.

［2］孟秀云.导弹制导与控制系统理论［M］.北京:北京理工大学出版社，2002.

［3］Gillybaeuf J P，Mansuy P，Pavsic S.Two new chimera methods-Application to missile separation，AAIA95-0353［R］.1995.

［4］Van Albada G D，Van Leer B，Roberts W W.Acomparative study of computional methods in cosmic gas dynamics［J］.ASTRON.ASTRO PHYS REV，1982，108(1):76－84.

［5］于长官.现代控制理论［M］.哈尔滨:哈尔滨工业大学出版社，1997.

［6］聂璐，向锦武.飞机外挂物投放安全性的参数影响分析［J］.飞行力学，2011，29(2):25－28.