刚性弹正侵彻细观模型混凝土靶弹道偏转因素分析*

杨 涛，姚 勇，邓勇军，周 晶，吴晓凤

(西南科技大学土木工程与建筑学院，四川绵阳 621010)

0 引言

自20世纪70年代开始，靶板侵彻问题一直倍受众多学者的关注。混凝土作为当前军事建筑物、交通要道及其他防护工程的主要建造材料，国内外研究者对其侵彻方面的问题做了大量研究，取得了相应的研究成果［1-3］。然而，现有的成果大多是基于宏观力学理论，假设混凝土材料为连续均匀建立的，认为弹丸侵彻过程中保持直线运动［4-7］。已有试验均表明［8-10］在侵彻过程中弹丸承受骨料及砂浆的非对称力影响，存在弯曲破坏，弹道发生较大偏转，不是一条直线，而是偏离轴线方向，这将极大影响弹丸精确打击目标的效果。发生上述现象是由于混凝土材料具有非均质的特殊性。对于这一问题，高政国、刘光廷［11］提出混凝土随机骨料模型，即往水泥砂浆中随机投放粗集料的方法。然而，随机骨料模型计算效率较低，耗时较长，故在混凝土细观构成对计算结果影响较小时，可考虑采用连续均匀模型用以计算。文中就连续均匀模型与随机骨料模型使用范围进行分析，提出连续均匀模型适用范围，供参考。

1 计算工况

1.1 几何模型

靶板随机骨料模型中用随机凸多面体模拟骨料的三维几何形状，随机凸多面体通过在八面体骨料基的基础上生长而成，砂浆和骨料间采用界面处理。靶板几何尺寸为400 mm×600 mm×200 mm，单元网格尺寸均为2 mm。弹体形状为尖卵形，CRH=3.0，直径为25.4 mm，长为143.7 mm，侵彻初始速度为300～1 200 m/s。为了更为普遍的分析不同弹体直径和不同着靶速度情况下弹体偏转角度值，定义参数弹径比γ=D/d，其中D为子弹直径，d为骨料最大粒径。在此基础上选择了四种不同γ弹径比为0.40、0.85、1.67及2.67为研究对象，以改变骨料最大粒径来实现，弹体着靶速度范围为300～1 200 m/s。为了减小计算量，计算采用1/2模型。

图1 侵彻模型

1.2 材料模型

混凝土靶板各相材料采用K ＆ C［12］本构模型，模型有8个独立参量，定义3个极限面的压缩子午线，见图2。

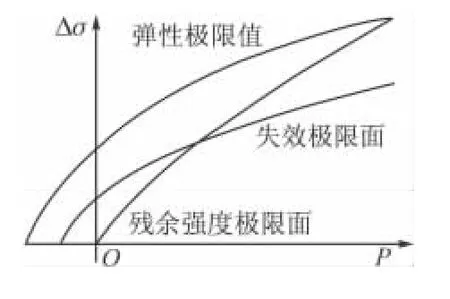
图2 K ＆ C模型的压缩子午线

模型的3个屈服面分别定义为:

式中:p 为静水压力;a0y、a1y、a2y、a0、a1、a2、a1f、a2f为材料常数。

3个极限面公式描述了混凝土在冲击作用下的非线性关系，后继屈服面和软化面对应的压缩子午线表示为:

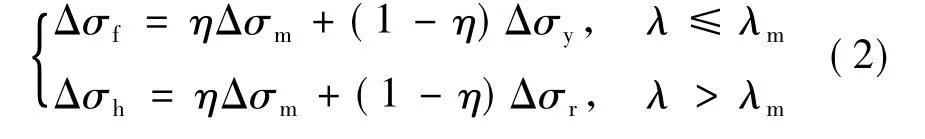
式中:λ为损伤变量，是关于等效塑形应变的函数;η为λ的函数，0≤η≤1;λm为损伤转折点。

混凝土拉、压损伤时，损伤变量λ可以分别表示为:

式中:dεp为等效塑形应变增量;bc为压缩软化系数;bt为拉伸软化系数;rf为单轴强度应变率效应增强系数。

混凝土应变率效应明显，其各相材料参数采用赵睿等［13］中提供的数据，见表1。

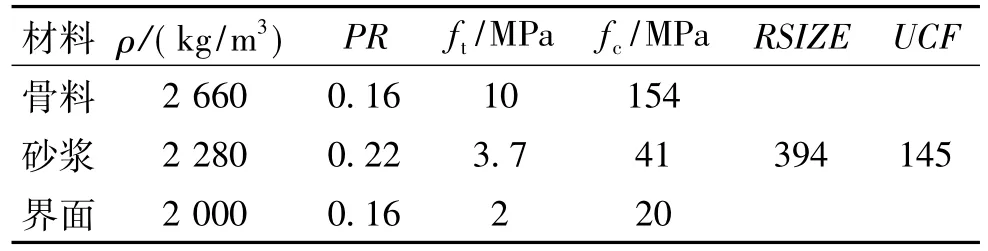
表1 K ＆ C模型中混凝土各相材料本构参数

采用刚性弹体，弹体密度为7.8×103kg/m3，杨氏模量为2.07 ×105MPa，泊松比为0.3。

3 刚性弹正侵彻弹体受力分析

陈小伟［14］等对刚性弹侵彻深度和阻力的比较进行了分析，求出了针对不同靶材刚性弹假设相应的速度阈值为vc，见式(4)。

式中:N1、N2为弹头形状与摩擦系数μ有关的无量纲形状参数;A，B为靶材的无量纲材料参数;σy为靶材的屈服应力;ρ为靶材的密度。

在着靶速度不大于vc时，可认为弹体侵彻过程中受到常阻力Fx作用，见式(5)。

式中:d为弹体直径。

针对本工况，可以认为在本次模型中刚性弹假设的速度范围为V＜1 200 m/s。此时，侵彻过程中的弹体被看作是刚性体，研究在此范围内影响弹体稳定性的因素。

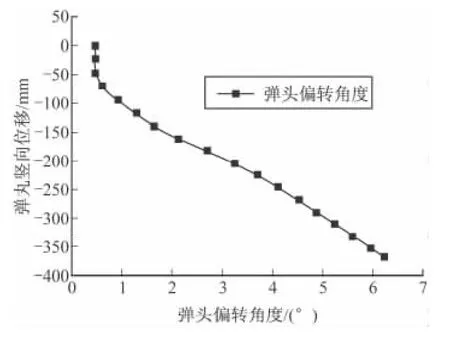
图3 弹头水平位移及偏转角度曲线

为了定量的说明该问题，选取弹体头部在侵彻过程中轴线上两端节点水平位移差随侵彻深度的变化曲线，并得到弹体偏转角度随侵彻深度变化曲线，见图3，从图中可以看出，弹体在初始的50 mm深度位置基本没有偏转，随着侵彻深度增加，水平方向位移及偏转角逐渐增大，根据美国圣地亚国家实验室试验及数值计算［15］表明:尖卵头弹着靶瞬间，靶表面附近首先产生崩落而形成约为弹体直径2倍深的入口漏斗坑，在弹头部周围经历较大径向压缩应力的材料在较高的压力下出现压碎失效。而在此区域以后，为隧道区，该区域被压碎的材料以颗粒重组的方式被压实，形成侵彻隧道壁，习惯上把0＜H＜2d的区域称为弹坑，而把2d＜H＜Hmax的部分称为弹洞。

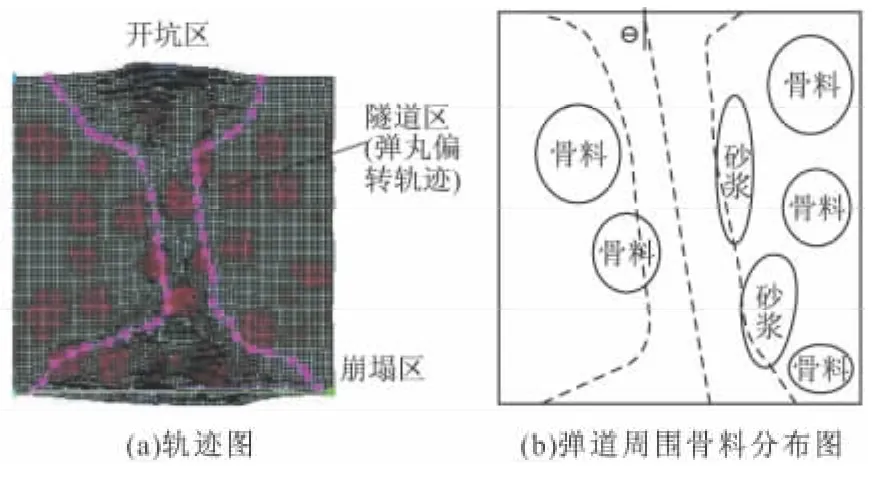
图4 隧道区弹道轨迹图

根据弹头偏转曲线，结合初始侵彻数据，可知当弹体在开坑区域时，即是竖向位移约为50 mm(2倍弹径，弹体直径为25.4 mm)，由于初始动能大，且弹体刚度相对混凝土各相材料大很多，混凝土细观非均匀性及随机分布对弹体偏转没有任何影响，此时混凝土中无论是骨料、砂浆、界面均被弹体压碎，弹体偏转角度为0，而当混凝土进入2d＜H＜Hmax时(隧道区)，图4(a)为800 m/s速度侵彻弹道，此时弹体动能逐渐减小，从图4(b)中可以直观的看出，弹道左边与弹体接触位置明显存在骨料，而右边主要是砂浆及界面，故基于上述现象分析，针对弹体偏转问题，给出弹体在随机骨料中的弹头简化受力模型(见图5)，探讨弹体在侵彻过程中影响弹体偏转的主要因素。

在连续均匀介质模型中，弹体所受阻力可以分为两部分:一部分是弹体头部的侵彻阻力，包括法向和切向阻力，另一部分是来自弹体侧壁动态摩擦粘滞阻力，而弹体头部的法向阻力是根据空腔膨胀理论所得，在正侵彻条件下，各个部位受力对称，弹头磨蚀程度对称，弹体基本不发生偏转现象，实际情况中由于骨料、砂浆、界面三相材料存在差异，各部分提供给弹体的空腔膨胀应力不相等，正侵彻时弹体所受的力并不对称，弹体发生偏转现象。

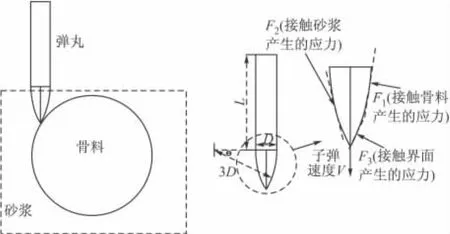
图5 弹体侵彻过程中简化受力模型

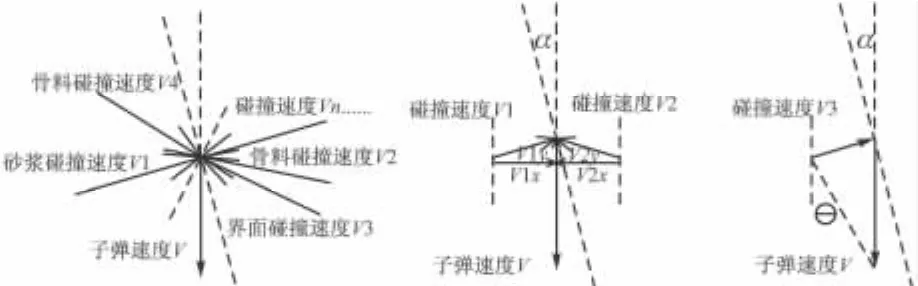
图6 弹体受力示意图

空腔膨胀理论表明:空腔膨胀速度v和空腔表面法向应力之间的关系可以用式(6)表示，这个关系可以用来描述弹头阻力与弹体侵彻速度:

式中:静阻力系数A与空腔周围的材料性质相关，动阻力系数B跟弹头形状相关，Yt为靶材的屈服强度，ρt为靶材密度，v为侵彻过程中弹体瞬时速度，第一项是空腔膨胀需要的最小临界应力，且根据陈小伟等研究表明在刚性弹假设中侵彻阻力可以只考虑第一项，即准静态阻力部分(材料动强度项)，该部分表明弹体受到的空腔阻力只与周边的材料性质有关。

据式(6)可知，弹体头部受到的法向应力与周围的材料性质、屈服强度、密度等有较大关系，而骨料、砂浆及界面3种材料各自属性相差较大，从而导致其提供给弹体的空腔应力不同，且侵彻过程是一个高速撞击的受力过程，可通过图6来描述弹体在接触骨料、砂浆及界面时的受力情况，总结弹体偏转原因:高速碰撞产生瞬时冲量Ft=MVn，对于弹体来说形成瞬时速度分量Vn(且骨料、砂浆及界面三者产生σn不同，则相应的速度有 V1，V2，…，Vn)，在弹体初始侵彻速度V一定的情况下，Vn的大小与作用方向直接决定了弹体偏转的角度，Vn的大小与F、M、t有关。对于弹体高速撞击混凝土，由于弹体强度、弹性模量等远远大于骨料及砂浆，故可认为弹体与骨料、砂浆接触时间t近似相等，Vn的作用方向与弹头表面各处切线有关(图6中α)。

3 弹径比对偏转角影响分析

不同速度下4种弹径比弹体侵彻时间-偏转角度曲线如图7，从图中可以得出以下几个规律:

1)同一速度下，弹体偏转角度随弹径比增大而逐渐减小，并且当弹径比增大到1.67时，偏转角度基本上在1°以内，当弹径比增大到2.67时，几乎没有偏转，这是由于弹径比过大，在速度一定的情况下，弹体质量大，初始动能高，骨料、砂浆及界面碰撞带来的速度分量相对于初始速度小得多，故此时形成的偏转角度几乎可以忽略，故可以认为该条件下可以不考虑混凝土细观组成对于侵彻过程中弹体偏转的影响，采用连续均匀模型进行模拟即可;

2)同一弹径比下，当弹径比小于1.67时，随着速度的增加，偏转角度有较大增长，其中弹径比为0.4，速度为1 200 m/s时偏转角度已经达到38°;当弹径比在1.67及以上时，偏转角随着速度的增加基本没有变化，这与第一点相同;结合第一点分析可知，在刚性弹假设范围内，若弹径比γ达到2或者以上时，弹体的偏转角度基本可以忽略不计，此时混凝土细观组成对于弹体偏转影响较小，可以看作均匀介质，采用普通的连续均匀模型即可，且速度的增加对偏转角影响较小，基本可以忽略;若弹径比γ小于2时，弹体的偏转角度不能忽略，此时混凝土细观组成对于弹体偏转影响很大，采用随机骨料模型才能描述弹体偏转及弹道轨迹变化，且速度的增加对偏转角影响较大。

3)弹体姿态在最初的一段时间内改变很小，基本上没有变化，这与观察到的侵彻弹道在初始侵彻阶段近似为直线的现象吻合，当弹撞击速度较低时，侵彻过程中弹偏转角的波动较大，这表明低速侵彻过程中弹的运动趋势由于弹体的非对称受力而容易改变。当撞击速度增高时，弹偏转角的绝对值增加，偏转角的波动减小，当撞击速度达到1 200 m/s时，弹偏转角逐渐增加(沿同一方向)，基本上没有波动，表明高速侵彻时弹的运动趋势不容易改变。这是由于弹高速侵彻靶体过程中，当弹由于撞到骨料产生初始偏转后，便由原来的正侵彻转变为非正侵彻，由于弹体撞击速度较高，非正侵彻时作用在弹体上的侧向阻力相对低速时更大，侵彻过程中，即使弹撞到偏转方向一侧的骨料上受到相反方向的偏转力，但由于作用时间极短且沿偏转方向的侧向阻力较大，使得弹的姿态不会向相反方向偏转，而是沿原来的偏转方向缓慢增加。

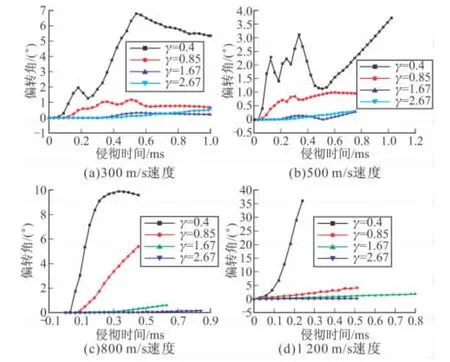
图7 不同速度下四种弹径比弹体时间-偏转角度曲线

4 结论

通过以上分析，可以得到以下关于此次刚性弹正侵彻混凝土靶模拟的结论:动能弹弹径比小于2，混凝土细观组成极大程度促进弹道偏转，并且着靶速度对弹道偏转稳定性影响十分显著，采用细观混凝土模型模拟是有意义的;弹径比不小于2，混凝土细观组成对弹道影响较小，并且着靶速度对弹道偏转稳定性影响较小，可考虑采用均匀介质模型模拟。

［1］Forrestal M J，Cargile J D，Tzou R D Y.Penetration of concrete targets［R］.Sandia National Labs，NM(United States)，1993.

［2］Kennedy R P.A review of procedures for the analysis and design of concrete structures to resist missile impact effects［J］.Nuclear Engineering and Design，1976，37(2):183-203.

［3］Hanchak S J，Forrestal M J，Young E R，et al.Perforation of concrete slabs with 48 MPa(7 ksi)and 140 MPa(20 ksi)unconfined compressive strengths［J］.International Journal of Impact Engineering，1992，12(1):1-7.

［4］Chen X W，Li Q M.Deep penetration of a non-deformable projectile with different Geometrical characteristics［J］.International Journal ofImpact Engineering，2002，27(6):619-637.

［5］陈小伟.穿甲/侵彻问题的若干工程研究进展［J］.力学进展，2009(3):316-351.

［6］陈小伟，杨世全，何丽灵.动能侵彻弹体的质量侵蚀模型分析［J］.力学学报，2009，41(5):739-747.

［7］He L L，Chen X W.Analyses of the penetration process considering mass loss［J］.European Journal of Mechanics-A/Solids，2011，30(2):145-157.

［8］何翔，徐翔云，孙桂娟，等.弹体高速侵彻混凝土的效应实验［J］.爆炸与冲击，2010，30(1):1-6.

［9］黄民荣.刚性弹体对混凝土靶的侵彻与贯穿机理研究［D］.南京:南京理工大学，2011.

［10］赵晓宁.高速弹体对混凝土侵彻效应研究［D］.南京:南京理工大学，2011.

［11］高政国，刘光廷.二维混凝土随机骨料模型研究［J］.清华大学学报:自然科学版，2004，43(5):710-714.

［12］Malvar L J，Crawford J E，Wesevich J W，et al.A plasticity concrete material model for DYNA3D［J］.International Journal of Impact Engineering，1997，19(9):847-873.

［13］赵睿，姚勇，邓勇军.K ＆ C模型的随机骨料混凝土侵彻应用［J］.四川兵工学报，2013，34(1):105-107.

［14］陈小伟，李继承.刚性弹侵彻深度和阻力的比较分析［J］.爆炸与冲击，2009，29(6):584-589.

［15］Forrestal M J，Frew D J，Hanchak S J，et al.Penetration of grout and concrete targets with ogive-nose steel projectiles［J］.International Journal of Impact，1996，18(5):465-476.