一类时滞SIQRS网络病毒传播模型的稳定性和Hopf分支*
尹 发,张子振,王丽叶
(安徽财经大学管理科学与工程学院,安徽 蚌埠,233030)
引言
近年来,基于网络病毒的传播与传染疾病的传播相似性,有不少研究学者提出了不同的计算机网络病毒传播模型,研究计算机网络病毒的传播行为.文献[1]研究了一类改进的SIR网络病毒传播模型的稳定性,并给出产生分岔的充分条件.文献[2]和文献[3]分别研究了一类具有直接免疫的SIR和SIRS网络病毒传播模型.考虑到网络病毒的潜伏期,文献[4]则在SIR网络病毒传播模型的基础上,提出了一类SEIR网络病毒传播模型,并研究了模型的有病毒平衡点的稳定性.但是,以上网络病毒传播模型并未考虑到时滞因素.考虑到网络病毒的潜伏期时滞,文献[5]提出并研究了一下具有隔离策略的时滞SIQR网络病毒传播模型:

其中,S(t),I(t),Q(t)和R(t)分别表示易感状态、感染状态、隔离状态和恢复状态节点在时刻t的数量.b,p,β,d,α1,α2,γ,δ和ε为系统(1)的参数,均具有和文献[5]相同的物理含义.τ为网络病毒的潜伏期时滞.文献[5]研究了系统(1)的全局吸引性和持续性,得到了一些有益的结果.显然,系统(1)是假设处于恢复状态的节点对网络病毒具有永久的免疫力,这与现实中的网络世界是不相符的.基于此,并考虑到恢复状态的节点对网络病毒的临时免疫期时滞,本文提出下列具有临时免疫期时滞的SIQRS网络病毒传播模型:

其中,η为恢复状态节点向易感节点的转化率,τ为恢复状态节点的临时免疫期时滞.
1 有病毒平衡点的稳定性和Hopf分支的存在性
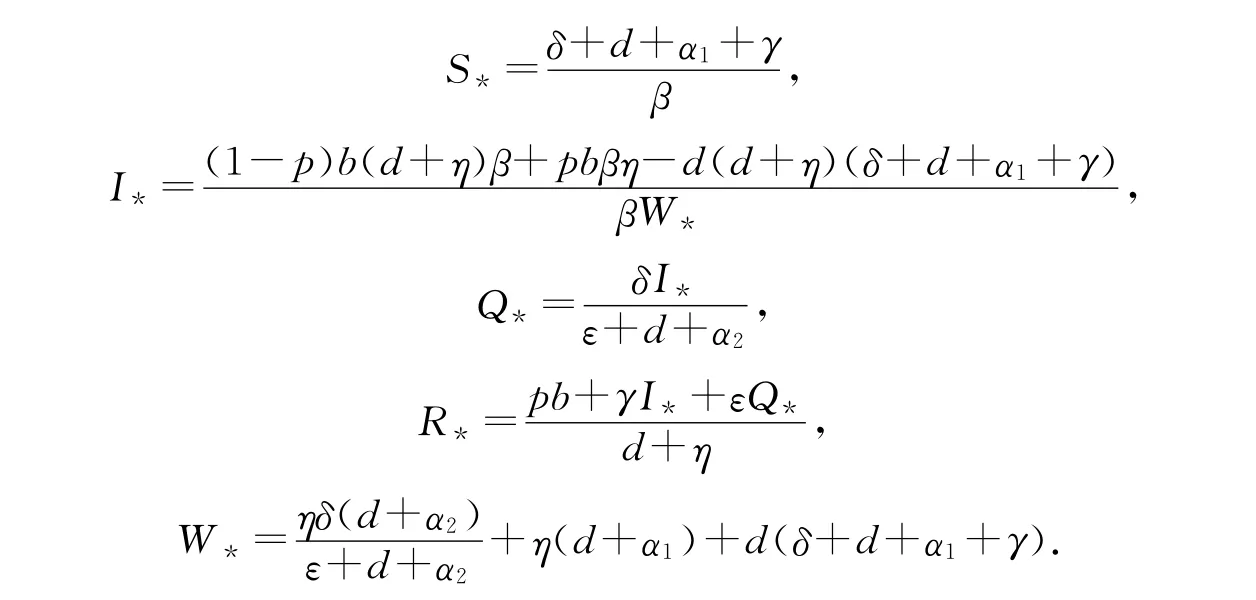
系统(2)在有病毒平衡点D*处的线性化系统为

其中

系统(3)的特征方程为:

其中:
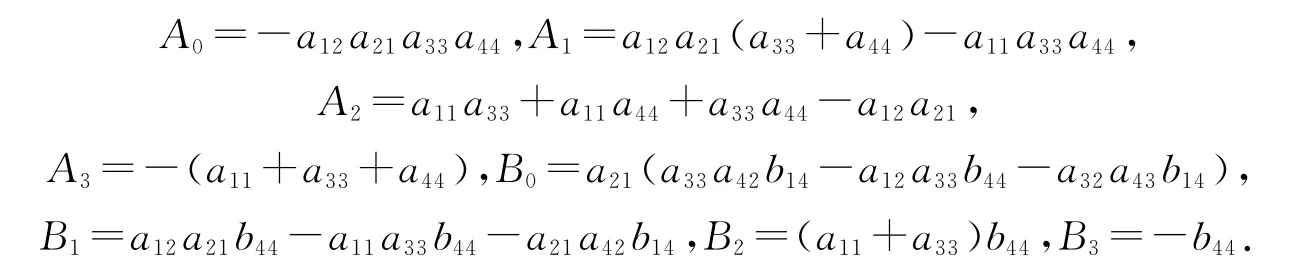
当τ=0时,方程(4)变为

其中:
A0*=A0+B0,A1*=A1+B1,
A2*=A2+B2,A3*=A3+B3.
根据A3,B3的表达式可以得到A3+B3=3d+α2+ε+η+βI*>0.因此,如果条件(H1)(其中,条件(H1)即:方程(6)~(8))成立,则系统(2)的有病毒平衡点D*是局部渐近稳定的.

当τ>0时,令λ=iω(ω>0)为方程(4)的一个根.则可以得到:

进而,得到

其中,

令ω2=v,则方程(10)变为

关于方程(11)根的分布,类似于文献[6]中的讨论.根据文献[6]中的讨论结果,并考虑到如果系统(2)的所有参数值给定,那么方程(11)的根很容易由Matlab软件计算得到.因此,为了给出本文主要结果,做出下列假设:
(H2):方程(11)至少存在一个正实根.
如果条件(H2)成立,即方程(11)至少存在一个正实根,则方程(11)至少存在一个正实根v0使得方程(4)存在一对纯虚根对于ω0,根据方程(9)可以得到相应的时滞临界值

因此,

对方程(4)左右两边同时求λ关于τ的导数,可以得到

因此,

因此,如果条件(H3),即,f′(v*)≠0,成立,则根据文献[7]中所介绍的Hopf分支定理可以得到下列结论.
定理1 如果条件(H1)~(H3)成立,则当τ∈[0,τ0)时,系统(2)的有病毒平衡点D*(S*,I*,Q*,R*)是渐近稳定的;当τ=τ0时,系统(2)在有病毒平衡点D*(S*,I*,Q*,R*)处产生Hopf分支,并在τ=τ0附近产生一簇周期解.
2 仿真示例
令b=10,d=0.01,p=0.2,α1=0.01,α2=0.02,β=0.1,γ=0.5,δ=0.1,ε=0.1,η=0.5.可以得到系统(2)的一个仿真示例:

利用Matlab软件经过计算可以得到,R0=160.657 8>1并得到系统(12)的唯一有病毒平衡点D*(6.2,182.238 3,140.183 3,210.073 5),并且可以验证条件(H1)是成立的.进而,有ω0=1.002 9,τ0=9.667 2.根据定理1可知,当τ∈(0,9.667 2)时,系统(12)是渐近稳定的,当τ>τ0=9.667 2时则系统(12)失去稳定性,并产生Hopf分支.仿真效果如图1~4所示.

图1 当τ=8.35∈(0,9.667 2)时,系统(12)SIQ相图

图2 当τ=8.35∈(0,9.667 2)时,系统(12)IQR相图

图3 当τ=12.25>τ0=9.667 2时,系统(12)SIQ相图

图4 当τ=12.25>τ0=9.667 2时,系统(12)IQR相图
3 结论
基于文献[5]中所提出的SIQR网络病毒传播模型,并考虑到网络中恢复状态节点对病毒的临时免疫期,本文提出了一类具有临时免疫期时滞的SIQRS网络病毒传播模型.首先给出有病毒平衡点存在的条件,进而以恢复状态节点的临时免疫期时滞为分支参数,通过分析相应特征方程根的分布,讨论了有病毒平衡点局部渐近稳定性和Hopf分支的存在性,得到有病毒平衡点局部渐近稳定性和Hopf分支存在的充分条件.最后,给出一个仿真示例对所得理论分析结果的正确性进行了验证.Hopf分支的发生,将不利于控制网络病毒传播有效措施的制定.因此,应该采取有效措施对系统(2)Hopf分支的产生进行控制.
[1]Piqueira J.R.C,Araujo V.O.A modified epidemiological model for co mputer vir uses[J].Applied Mathematics and Co mputation,2009,213(2):355-360.
[2]肖丽,包骏杰,冯丽萍.一种新的计算机病毒模型的稳定性分析[J].湘潭大学自然科学学报,2012,34(2):94-96.
[3]叶晓梦,杨小帆.基于两阶段免疫接种的SIRS计算机病毒传播模型[J].计算机应用,2013,33(3):739-742.
[4]Peng M,He X,Huang J.J,Dong T.Modelling computer virus and its dynamics[J].Mathematical Problems in Engineering,vol.2013,Article ID 842614,5 pages.
[5]杨斌.具有时滞的SIQR计算机病毒模型分析[J].重庆工商大学学报(自然科学版),2013,30(9):70-73.
[6]Li X.L,Wei J.J.On the zer os of a fourth degree exponential polyno mial with applications to a neural net wor k model with delays[J].Chaos,Solitons and Fractals,2005,26(2):519-526.
[7]Hassard B.D,Kazarinoff N.D,Wan Y.H.Theory and Applications of Hopf Bif urcation[M].Cambridge University Press,Cambridge(1981).

