坐标本征态的Fock表象表示*

林 蓉

(菏泽学院物理与电子工程系，山东菏泽274015)

引言

Dirac证明了薛定谔的波动力学与海森堡的矩阵力学的统一性，并且创造性的引入了Dirac符号，Dirac符号是量子力学理论最普遍的表述［1］．许多教材［2～4］阐述了波函数在不同表象中，如动量表象、角动量表象等的表示形式，由此可以得出描述微观粒子的态可以在任何表象下表示出，即态矢不依赖于任何表象．本文利用线性谐振子本征态│n〉的完备性导出了坐标本征态│x〉在Fock表象下［5］的表达式．在Fock表象中计算简洁，而且用途越来越广．

1 薛定谔方程

在量子力学中，微观粒子的状态大多用波函数描写，但决定粒子状态变化的是薛定谔方程，它描写势场U→)中粒子状态随时间的变化．

薛定谔方程为:

如果U(→r)不含时间则(1)式的解可用分离变量法进行简化，考虑一特解

将(2)式代入(1)式并对方程进行计算可得到定态薛定谔方程:

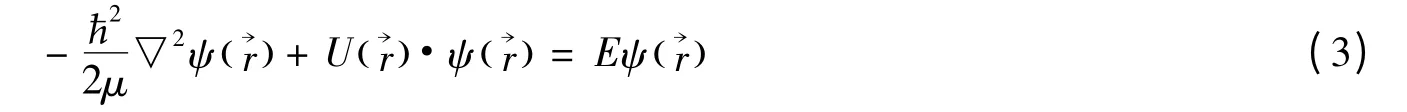
所谓定态就是指能量具有确定值的状态．

2 狄喇克符号

在几何学或经典力学中，常用矢量形式讨论问题而不指明坐标系，同样，在量子力学中，描写态和力学量也可以不用具体表象，这种描写方式是狄喇克最先引用的，因此这样的一套符号称为狄喇克符号．

微观体系的状态可以用一种矢量来表示，它的符号是│〉，称为刃矢，简称刃，也称为右矢，某一确定的刃矢A可用符号│A〉表示．微观体系的状态也可以用另一种矢量来表示，这种矢量的符号是〈│，称为刁矢，简称刁，也称为左矢，某一确定的刁矢B可用符号〈B│表示．

刃和刁是两种不同的矢量，二者不能相加，它们在同一种表象中的相应分量互为共轭复数．│A〉在Q表象中的分量为{a1，a2，…an…}，那么〈A│在Q表象的分量为}．和│A〉〈B│在同一表象中相应分量的乘积之和称为│A〉和〈B│的标积，用符号〈B|A〉表示．用表示〈B│在Q表象中的分量，那么显然〈B│A〉和〈A│B〉互为共轭复数，即:

设│A〉为表示某一状态的刃，这个态在x表象中以波函数Ψ(x，t)描写，Ψ(x，t)就是刃│A〉在x表象中的分量，由于基刃│x〉组成完全系，所以│A〉可以按│x'〉展开:

以〈x│左乘上式两边，并且利用坐标x的本征态正交归一条件:

可得:

由(4)式和(7)式可得:

3 Fock表象的引入

量子力学中态和力学量的具体表示方式称为表象．常见的表象有坐标表象、动量表象、能量表象、角动量表象和Fock表象．

3．1 线性谐振子

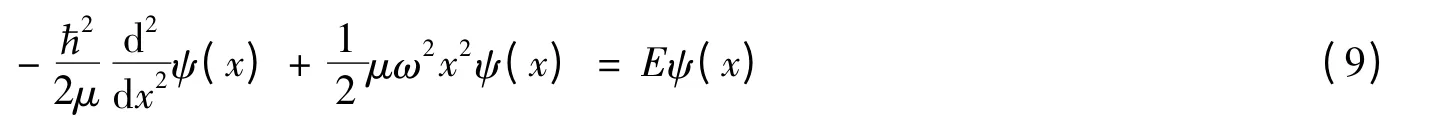
引入没有量纲的变量ξ代替x，它们的关系是

其中Hn(αx)为厄密多项式，Nn是归一化常数，且

Hn(ξ)=Hn(αx)满足递推关系［6］:

3．2 本征矢│n〉的封闭性

Q表象的正交归一基矢全体集合为{│n〉，n=1，2，3…}，是完备的，任意态矢│ψ〉可以通过│n〉表示为因为│ψ〉是任意的，故

(15)式所表示的性质称为本征矢│n〉的封闭性，也称为完备性．通常将这组正交、归一、完备基{│n〉}所张的空间称为Fock空间．在Fock空间中，计算简洁，富于粒子图像，后继量子力学中经常使用，且用途越来越广．

3．3 Fock表象

引入新算符

利用(10)式可将(16)、(17)式改写为:

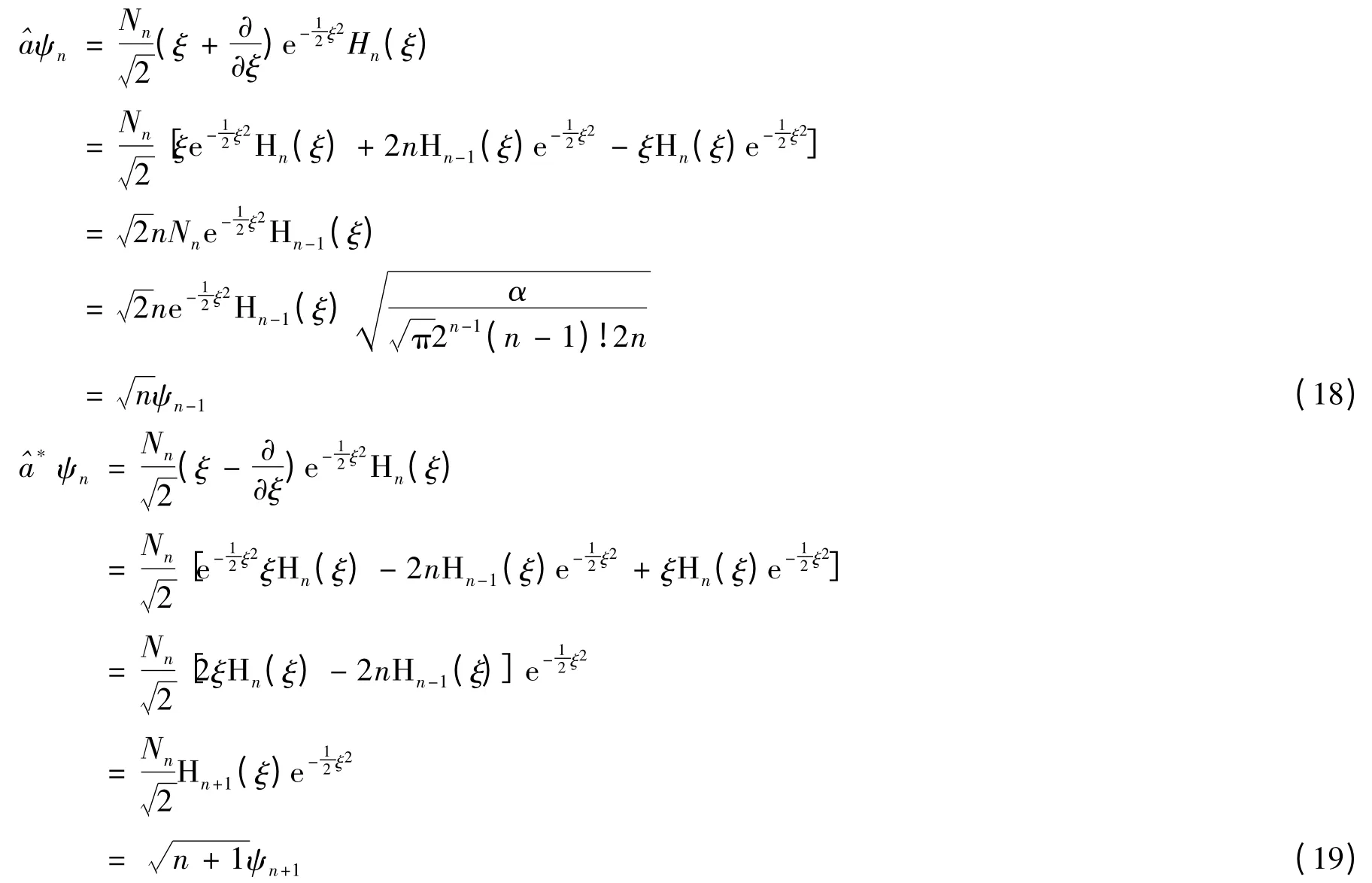
由(16)、(17)两式可得:

以│n〉为基矢的表象称为Fock表象，也称占有数表象．

4 坐标本征态的Fock表象表示

利用本征矢│n〉的封闭性:

和

以及

可得:

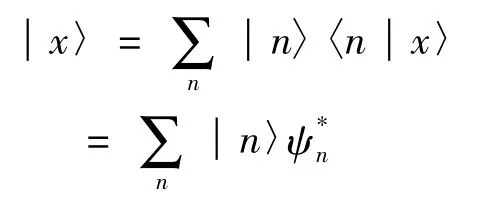
由于Ψn是实函数，所以=Ψn;

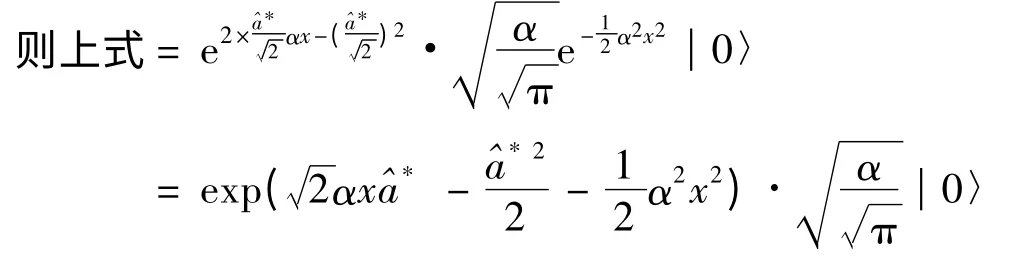
坐标本征态的Fock表象表示为:

综上所述，利用线性谐振子本征态的完备性和厄米多项式的母函数得出了坐标本征态在Fock表象中的具体表达式，方法简洁，易于接受，并且此表达式在量子力学研究的各个领域有着重要的应用．

［1］Dirac PA M．The principles of Quantum Mechanics［M］．Oxford:Clarendon Press，1930．

［2］曾谨言．量子力学(卷Ⅰ)［M］，第四版，北京:科学出版社，2007:128－137．

［3］周世勋．量子力学教程［M］，北京:高等教育出版社，1979，2:103－111．

［4］陈鄂生．量子力学基础教程［M］，第三版，济南:山东大学出版社，2006，1:139－152．

［5］袁洪春，王帅，范洪义．从二维正态分布密度函数的角度研究量子力学基本表象［J］．大学物理，2011，30(12):1－3．

［6］梁昆淼．数学物理方法［M］，第三版(修订本)，北京:高等教育出版社，1998:270－292．