基于收益率的股票相关性计量分析*

朱家明，刘红杉，朱运良，程瑶瑶，于静

(1．安徽财经大学统计与应用数学学院，安徽 蚌埠233030;2．安徽财经大学会计学院，安徽 蚌埠233030)

股票间的相关性对于风险管理、投资决策具有重要影响．对于股票相关性的研究，现代金融理论主要基于经济基本面进行解释，即认为相关性来源于影响资产现金流和影响资产折现率的基本面因素．股票市场作为复杂系统日益受到人们的关注，近年来，经济、数学、社会等领域的学者都开始用复杂网络及其相关概念来研究股票市场，进而研究股票间相关性．

1 数据的获取及假设

数据来源于安徽财经大学2014暑期数学建模模拟题［1］．为了便于解决问题，提出了以下假设:1)股票数据可以简单地看成时间序列数据，节假日的休市也不对股票序列的顺序产生影响;2)文中股票的变动只与自身和相关股票有关;3)以收益率为股票间相关性的度量指标能够很好的反映出股票间的相关性;4)Netdraw作图能够很好的反映变量组合间的关系．

2 补齐部分股票缺失的数据

2．1 研究准备

研究数据发现，考虑现金红利再投资的周个股回报率数据的缺少是由于缺少上周收盘价Pi(t－1)的数据，它与本周开盘价Qi(t)数值非常接近．首先把每只股票上周的收盘价Pi(t－1)减去本周的开盘价Qi(t)，将差值求和取平均，最后利用本周开盘价Qi(t)加上差值平均值来近似代替上周收盘价Pi(t－1)，即:

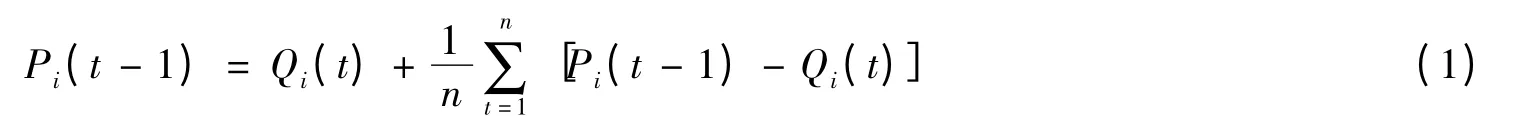
2．2 研究方法及结论

对于每只股票，考虑现金红利再投资的周个股回报率ai和不考虑现金红利再投资的周个股回报率bi相等，利用公式:，便可得到缺失的数据(见表1)．

表1 缺失的数据填充表

3 以收益率为指标度量股票间相关性

3．1 研究思路

现代投资组合理论中，人们用股票的预期收益率来描述预期收益，用收益率方差来度量风险，且线性相关系数越小，投资组合风险就越小，即收益率与股票的相关性大小关系密切，因此，选择股票收益率作为股票间相关性度量指标．

选取股票的收益率为度量指标，利用时间序列相关性知识，得出股票的相关系数矩阵［2］．

3．2 研究方法

选取第16周～第25周的没有缺失数据的所有股票来进行研究．利用公式计算股票收益率．

其中Pi(t)是股票i在第t周的周收盘价，Qi(t)是股票i在第t周的周开盘价，Ri(t)是股票i在第t周的周收益率．

cov(R1，R2)表示向量R1和R2间的协方差，σ1和σ2分别表示R1和R2间的标准方差，假设各数据的概率相等且为，则:

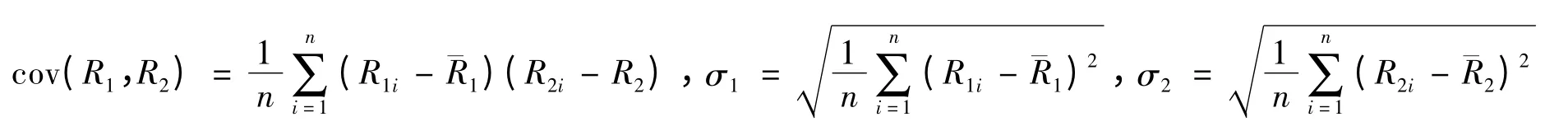
那么，相关系数为

3．3 研究结果

对上述模型，运用Matlab软件进行求解［3］，继而可得到股票的相关系数矩阵:

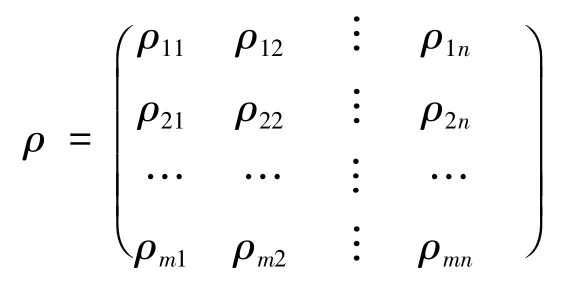
4 基于相关系数和最佳阈值的网络构建

4．1 研究思路

由于股票价格的缺失对于模型求解结果存在较大的影响，故要对数据进行预处理，选出合适的股票，根据每只股票的收益率，运用Matlab编程可求得股票间的相关系数矩阵．其次，在给定阈值0．5的基础上，选取一系列新的阈值，计算每个阈值下所构建网络的最大连通子图节点个数，选取其节点个数变化稳定时的阈值作为最佳阈值．最后，基于相关系数和最佳阈值来构建股票网络［4］．

4．2 研究方法

对前面所选取的数据，利用(3)式和Matlab编程，可求得解股票的相关系数矩阵:

股票代表网络中的点，如果相关系数ρ12≥θ(θ∈［－1，1］)，就认为节点i和j之间有连边，这里的θ即阈值点．阈值在一定区间变化时，网络是高度聚类的，具有明显的拓扑性质．

在给定阈值0．5的基础上，选取一系列新的阈值点，可求得每个阈值所构建的网络连接的总边数，近而比较不同阈值下的总边数变化(见表2)．

表2 不同阈值下所构建股票网络节点连接的总边数变化表

为直观了解阈值与股票数的相关关系，对表2利用Excel作图(见图1)．

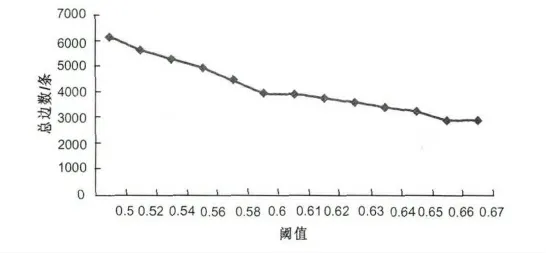
图1 不同阈值与所构建网络连接的总边数变化折线图

从图1可以看出，阈值在0．6以后，所构建的网络连接的总边数变化较平稳，并且可以看出阈值在0．657之前，最大连通子图的节点个数变化较快，到0．6时变化开始变得平缓．发现阈值为0．6时网络拓扑性质较稳定，因此选取0．6为最佳阈值．由此运用软件Netdraw可绘出基于相关系数和最佳阈值构建的股票网络(见图2)．

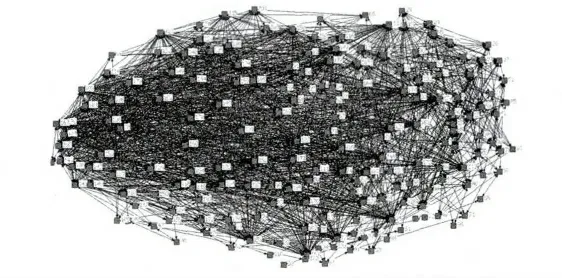
图2 基于相关系数和最佳阈值构建的股票网络

4．3 结果分析

当某些股票连接较多的节点时，这些股票的波动会直接影响着其他较多股票的走势．这些反映整体价格走势的点代表，相互连接程度高，股价的波动较容易在市场中传播．与其他股票交往频繁、联系紧密的节点，本文称作股票网络的核心节点;当某些股票的相邻股票节点数为2～4个时，它们沿分支方向调整和传递波动的信息，本文称作股票网络的中间节点;当某些股票只有一条边与其他节点连接时，则说明它与其他的股票交往较少，相关度不大，本文称作边界节点．

5 基于系统聚类法划分中国股票市场类型

5．1 研究思路

系统聚类法［5］基本思想是:聚类开始时将n个样品(或p个变量)各自归为一类，并规定样品(或变量)之间的距离和类与类之间的距离，然后将距离最近的两类合并成一个新类，计算新类与其他类之间的距离，重复进行两个最近类的合并，每次减少一类，直至所有的样品(或变量)合并为一类，最后形成一个亲疏关系图谱(见图3)．

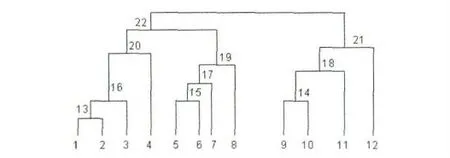
图3 最短距离法的聚类树型图

5．2 研究方法

本文采用最短距离法聚类，步骤如下:

1)将初始的每个样品各自作为一类，并规定样品之间的距离，本文采用欧氏距离．计算n个样品之间的距离矩阵D(0)，它是一个对称矩阵．其中，第i个样品Xi和第j个样品Xj之间的欧式距离定义为:

2)寻找D(0)中最小元素，设为DLK，将GK和GL聚成一个新类，记为GM，即GM= { GK，GL}．

3)计算新类GM与任一类GJ之间距离的递推公式为

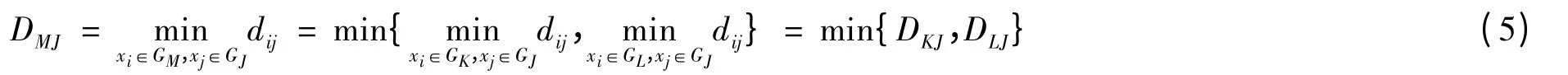
对距离矩阵D(0)进行修改，将GK和GL所在的行和列合并成一个新行新列，对应GM，新行和新列上的新距离由递推公式计算，其余行列上的值不变，这样得到的新距离矩阵记为D(1)．

4)对D(1)重复上述对D(0)的两步操作，得到距离矩阵D(2)，如此下去，直至所有元素合并成一类为止．

5．3 结果分析

运行Matlab编程，可求得部分系统聚类分析的结果(见表3)．

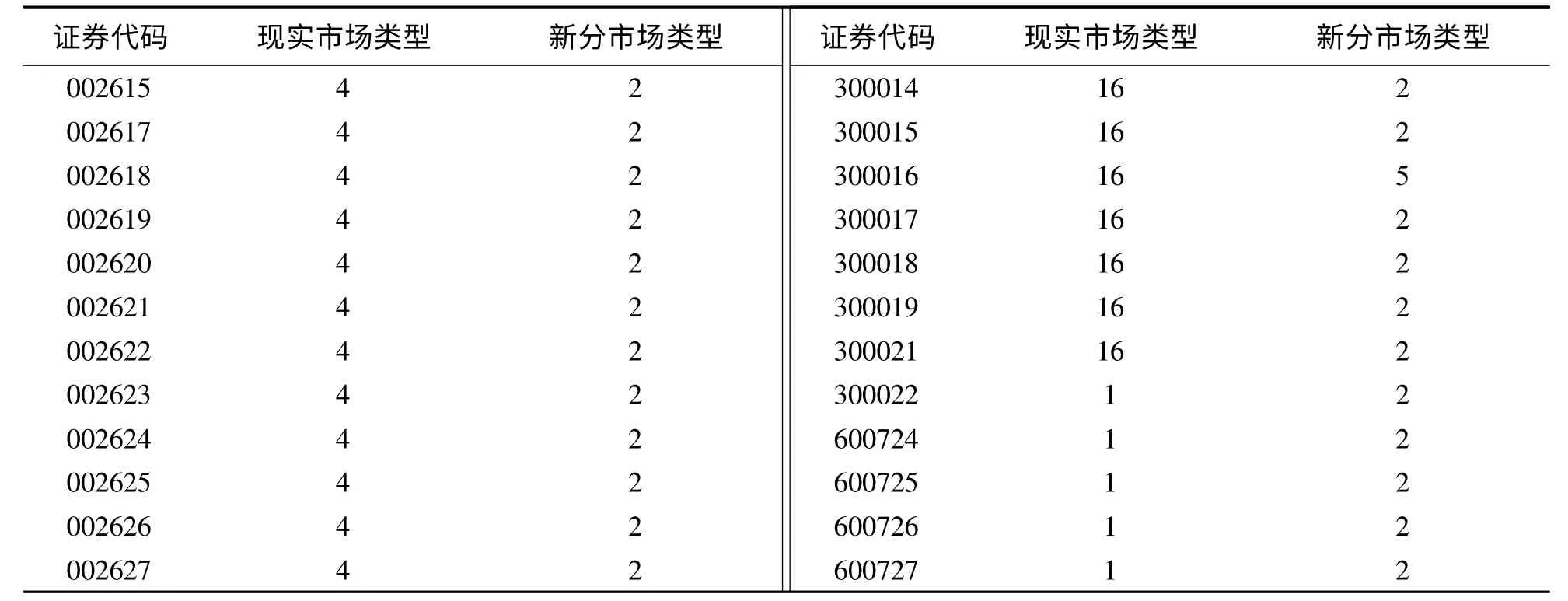
表3 部分聚类分析结果以及现实板块对比表

从表3中可以看出，所求得的股票板块划分结果与现实的有所不同，主要是由于划分标准不相同，上表所采取的划分标准是按股票的收益率，但是已有的结果是通过股票背后的市场类型来进行划分的．通过划分的结果与原来板块进行对比还可以发现，原来在同一板块的股票在划分之后基本上还在同一板块，这是由于同一板块的股票具有相似的变化趋势，原来板块内部股票的收益率也有一定相关性，这与本文的划分标准有重合点，这就是划分后每个版块的股票种类没有很大变化的重要原因．

6 结论

本文通过综合运用上述相关性分析、系统聚类分析、网络构建等方法，以收益率为指标，最终建立了基于相关系数和最佳系数的股票网络，为划分中国股票市场中的板块提供了可行性方案［6］．本文所建立的股票间相关性度量指标模型简洁便于理解，为股票之间的相互作用提供了理论基础，也为股票市场中股票投资组合风险的研究提供一定的研究基础．

［1］2014 年安徽财经大学数学建模模拟赛 A 题．［EB/OL］．http://zhujm1973．blog．163．com/blog/static/315513552014923288768．

［2］彭宏．股票数据流的相关性计算方法［J］．华南理工大学学报．2006，34(1):86－89．

［3］吴礼斌，闫云侠．经济数学实验与建模［M］．天津:天津教育出版社，2009．

［4］吴翎燕．基于相关系数和最佳阈值的股票网络模型构建［J］．复杂系统与复杂性科学，2013，10(4):49－55．

［5］谢中华．MATLAB统计分析与应用:40个案例分析［M］．北京:北京航天航空大学出版社，2012．

［6］王婷，朱家明，韦锐，等．中国GDP影响因素及可持续发展的计量分析［J］．菏泽学院学报，2014，36(2):8－15．