基于碳纳米传感器的复合材料内部缺陷测量及误差估计*

万 莉，马永军，李静东

(1天津科技大学计算机科学与信息工程学院，天津300222;2天津工业大学信息化中心，天津300387)

三维编织复合材料因设计性强、易于实现结构功能一体化设计与制备，已成为实现新型航天器结构和功能设计的首选材料。对于航空材料应用来讲，复合材料的用量及其性能水平已成为衡量其先进性的重要标志［1］。我国月球探测卫星“嫦娥一号”和“嫦娥二号”的空间桁架结构使用了我校研究生产的三维编织复合材料制件［2］。

碳纤维增强基复合材料结构较为复杂，其优良的性能和其质量的离散性以及高成本性并存，在制造和使用过程中，由于各种原因，纤维增强复合材料会生成各种不同类型的缺陷，比如分层、断裂或是不致密等。在材料制造过程中，不可避免产生各种各样的缺陷，对碳纤维复合材料的在役无损检测就显得格外重要［3］。作为航天主要承载材料，在其工作状态下必须建立完整的健康状态监测系统，连续实时监测局部损伤的发展状态，并进行定量评估。从而为材料结构的损伤检测提供准确信息，避免因复合材料结构破坏带来的巨大损失。研究开发高效的、实时的、连续的无损检测技术构成的健康监测系统对于复合材料结构损伤检查与持续监测有重要意义。

复合材料中的缺陷类型一般包括:裂纹、树脂开裂、断裂、胶接缺陷、空隙、分层、夹杂物、溢胶、脱胶、胶层超厚或超薄、纤维断裂与卷曲、贫胶、厚度偏离、磨损、划伤、树脂堆积、铺层皱折、凹坑、凸起、积瘤等。其中裂纹、断裂、空隙、分层等一般是航空复合材料构件上最主要的缺陷［4］。

复合材料常用的无损检测方法有超声波检测、X射线检测、声发射检测技术、激光全息检测、微波检测技术、光纤布拉格光栅等。光纤传感器计算出变化的应变在光的波长。许多光纤应变传感器已被证明有效的工作，包括微弯传感器、扭曲传感器、蚀刻传感器等。布拉格光栅光纤传感器可能是在结构一体化的最好的，因为他们提供了大量低带宽应变沿着一条光纤测量。它们可以用来测量纵向;应变与表面态状态，光纤应变传感器已被证实有许多优点，但光纤应变传感器光纤脆性，在处理困难并进行连接，由于大量的纤维，困难在测量不同方向的压力同样的位置，光解调器成本高。

由于三维编织复合材料结构的特殊性，这些方法往往具有检测时间长、精度低、检测过程复杂等缺点，这些传统方法在三维编织复合材料检测应用上具有一定困难［5－6］。

1991年日本NEC公司的饭岛纯雄(Sumio Iijima)首次利用电子显微镜观察到中空的碳纤维，该技术在复合材料监测就得到了应用［7］。文献［8］论述了碳纳米线复合材料的结构和电器特性，文献［9］描述了基于碳纳米线聚合物复合材料的界面进行了监测评价技术，它可用来检测拉伸和压缩载荷下的温度测量，结果表明增加纳米线复合材料的力学性能比环氧树脂或硅胶复合材料弹性模量要高。文献［10］描述了聚乙烯醇碳纳米线(聚乙烯醇CNT)嵌入到玻璃纤维增强塑料复合材料中用于复合材料损伤监测。测试的目的是寻求拉伸下聚乙烯醇纤维与碳纳米线的损伤程度。文献［11］论述了碳纳米线(CNT)的传感器集成到不同类型的聚合物中，文章论述了碳纳米线(CNT)纱线应变传感器复性和稳定性，提出了结构健康监测的开发方法，实验说明从77K至373 K的传感器可以很容易地嵌入到复合结构中，传感器具有高精度监测裂缝萌生的功能。文献［12］研究了整个结构中应变监控的方法，分析了碳纳米线传感器实现应变监测的可行性，研究提出了碳纳米线内置传感器为建构连续健康监测将提供一种新的综合和分布式传感器技术。

综上，国内外关于航空领域的传统复合材料状态健康监测应用研究取得了一定进展，近两年来国外学者对于碳纳米线的传感特性研究也取了很大进步，但未见关于碳纳米线在三维编织复合材料航天制件连续健康监测应用的文献报道。

随着三维编织技术和碳纳米线生产方式的不断发展，碳纳米线应用在三维编织复合材料结构健康检测中将会发挥越来越重要的作用。与传统的光纤传感器相比，碳纳米线具有耐久性和稳定性高的优点，特别适用在大范围分布式传感测量和复合材料的长期连续的状态健康检测中。

论文基于碳纳米线传感器，通过数理统计算法研究三维编织复合材料内部缺陷定位。

1 碳纳米线传感器嵌入方法研究

在三维矩形编织过程中，编织纱线由携纱器携带，并按预制件的截面形式排列。以三维编织四步法1×1方型编织为例，主体携纱器排布成m行和n列的主体阵列，附加携纱器间隔排列在主体阵列的周围。如图1所示，每一携纱器上携带一根编织纱线。编织过程由行和列按四步间歇编织运动实现。第一步，相邻的行相互错动一个编织动程。第二步，相邻的列相互错动一个编织动程。第三步和第四步分别与第一步和第二步相反。经过四步运动，完成一个机器编织循环，如图2所示。在一个机器循环中获得的预制件长度值定义为花节长度，用h表示。

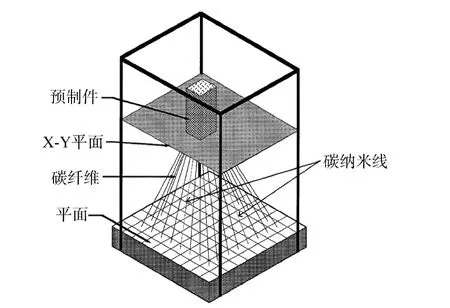
图1 三维编织复合材料编织图Fig.1 Schematic of a 3-D braiding set-up

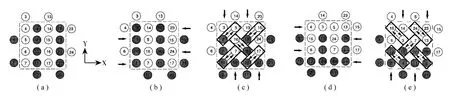
图2 预制件编织过程图(a)原始状态，(b)编织第1步，(c)编织第2步，(d)编织第3步，(e)编织第4步Fig.2 4-step process(a)Original configuration-Step 0，(b)Row movement-Step1，(c)Column movement-Step2，(d)Row movement-Step3，(e)Column movement-Step4

为实现三维编织复合材料制件的无损监测，将碳纳米线传感器与碳纤维共同编织，为全面实现制件实时检测，在编织纤维设置上，每隔一定间距设置一个碳纳米传感器。图1所示，每隔5个碳纤维纱放置一个碳纳米线传感器。由于碳纳米线纤维在编织过程中是连续的，因此，可实现整体制件的连续监测。

三维编织复合材料是由三维编织预制件增强的一种新型复合材料，三维编织复合材料预制件表面编织角是重要的结构参数之一。表面编织角是编织纱线在表面沿织物成形方向的夹角，见图3中的θ角。

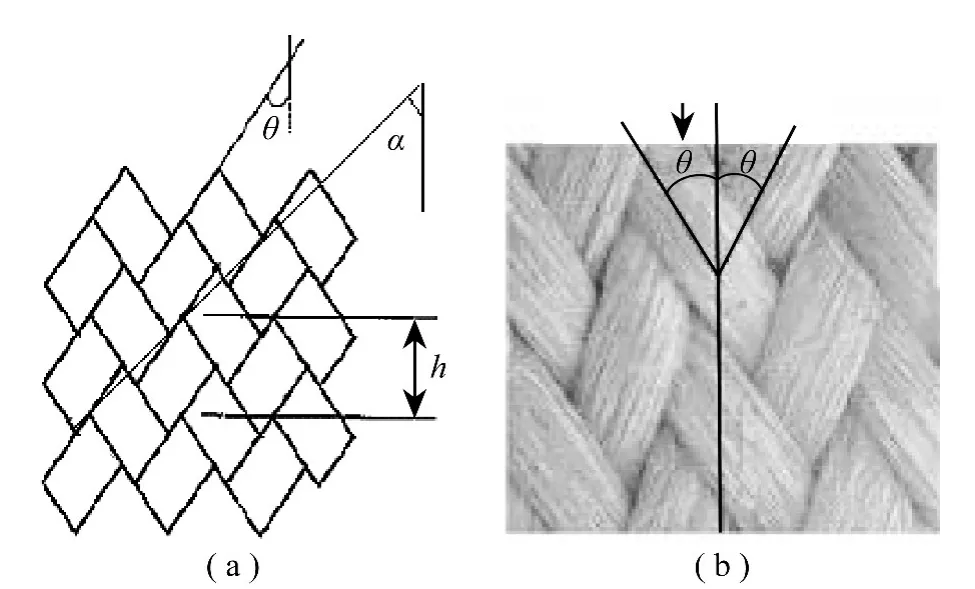
图3 三维编织复合材料预制件参数示意图(a)编织角和花节长度，(b)实际编织预制件Fig.3 The diagram of parameters of 3-D braided composite material preform(a)Braiding angle and pitch，(b)The actual braiding preform

为实现三维编织复合材料制件的健康检测，把碳纳米线传感器与碳纤维与其编织，为全面实现制件检测，在编织布线时，寻求合理的间距设置碳纳米传感器嵌入预制件中。

预制件中编织纱线的总根线N为:

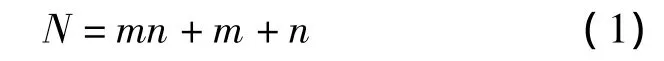
假设碳纳米线传感器的间距为K，则碳纳米线传感器数量为:

前期研究表明表面编织角θ和内部编织角α之间的关系为:

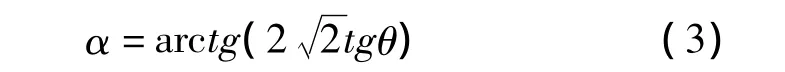
假设预制件的截面宽度(W)和厚度(T)给定后，需要根据用纱规格推导出用纱根数m、n的计算公式，以便确定携纱器数量及排列。在四步法三维编织结构预制件中，纤维束的倾斜角是一致的，外表面四面外观相同。总体结构各向均匀，其宽度与厚度的比值在足够大时，近似等于纱数比，即:

假设纤维束的排列为m×n，预制件的外形尺寸与单元体的几何尺寸有着直接的关系，可以得出用纱根数的计算公式为:

2 嵌入碳纳米线传感器的特性研究

2.1 嵌入碳纳米线传感器长度研究

已知三维编织预制件的表面编织角θ，预制件总长度H，碳纳米线纤维束细度一定。则可以计算单根碳纳米线的长度L为［13］:

为了精确计算用纱量L，需已知主体纱m与n数目。如图1所示，h为花节长度，当经过i次编织循环后，对于内部碳纳米线而言，一次编织循环用纱量为 LI，1:

则一个编织循环中，碳纳米线总长度 LS，I，1为:

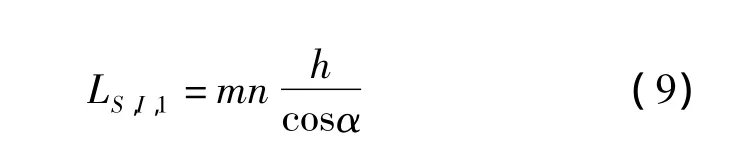
同理:对于表面纤维束而言，一次编织用纱量为 LO，1:

则一个编织循环中，表面碳纳米线总长度为LS，O，1:

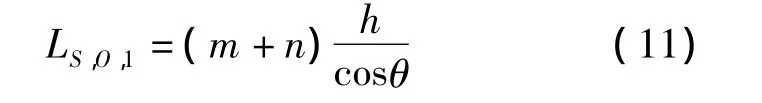
这样，编织一个花节长度用纱总量LS，1为:

所以i次循环后，预制件长度为H，总用纱量LS为:

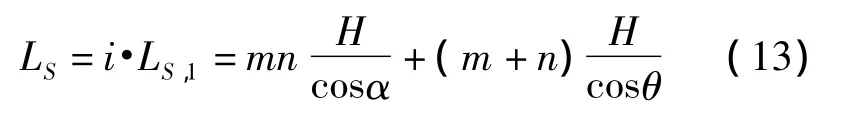
则需要单根碳纳米线长度L为:

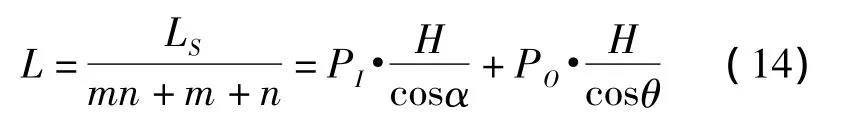
式中:PI为内部纤维束占纤维束总量的百分率，PO为表面纤维束占纤维束总量的百分率。

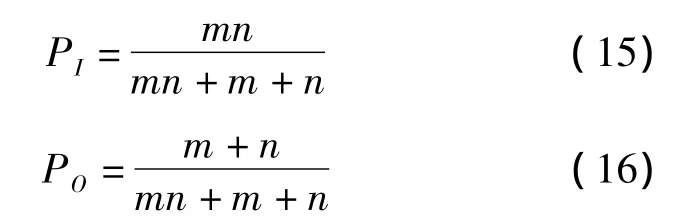
在实际编织过程中，存在编织余量及碳纳米线的连接，在研究中采用:碳纳米线长度 =计算长度+50(mm)。

2.2 碳纳米线传感特性分析

碳纳米线在应变15%～20%情况下才会破坏［9］。在应变小于10%情况下，碳纳米管可以在卸载时恢复原来的截面，这种特性使其在诸如高强度复合材科的制造中和纺织原料的纺织中具有极大的吸引力。可以与碳纤维共同编织，可对基体起到强化作用，而不影响三维编织复合材料的力学性能。

考虑到欧姆定律:

R为阻抗，ρ是电阻率、L的碳纳米线长度，A是碳米管截面积。电阻的变化可描述为:

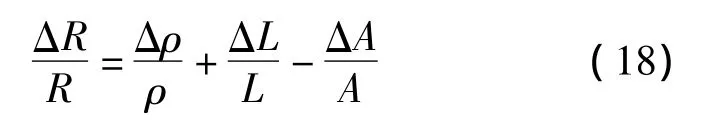
碳纳米线出长度变化可描述为:

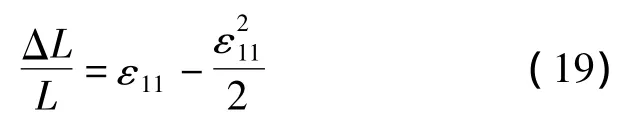
如果第二部分变形较小，可以忽略不计。由于泊松效应，碳纳米线的截面变化是横向各向同性的，传感器截面可表示为:

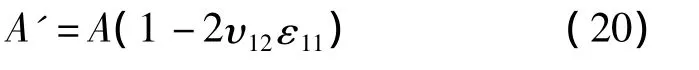
υ12为碳纳米线泊松比，则:

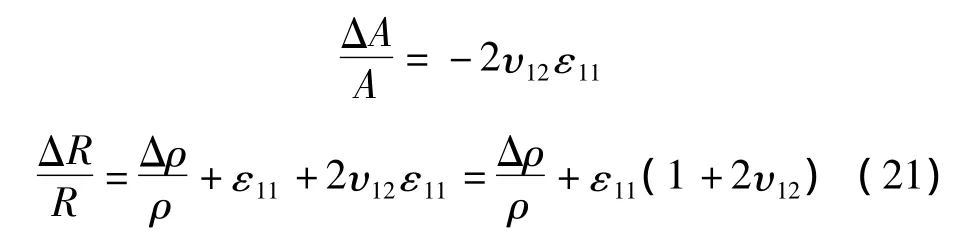
电阻的变化有两个原因，一是应变的产生，一是电阻率的变化。由于材料的承载和相对电阻率增量具有对称性，因此碳纳米线传感器在一定承载范围内具有较好的线性关系［9］。

每个碳纳米线传感器由一个碳纳米线和两个端线连接器组成，图4显示了传感器连接图。

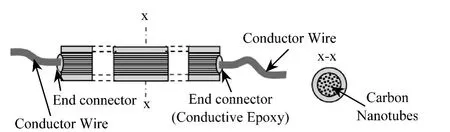
图4 碳纳米线传感器连接图Fig.4 The connection of carbon nanotube thread sensor

基于碳纳米线三维编织复合材料制件健康监测信号采集电路如图5所示。

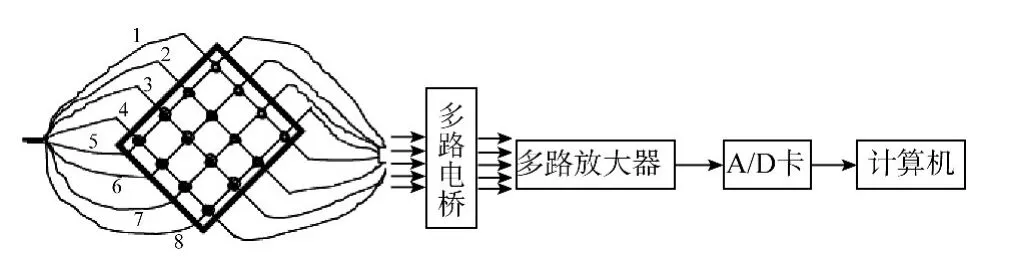
图5 碳纳米线三维编织复合材料制件缺陷检测图Fig.5 Schematic diagram of defects detection of 3-D braided composite material using carbon nanotube thread

3 三维编织复合材料的结构的损伤定位研究

论文依据天津工业大学大学开发的计算机控制的三维编织复合材料矩形编织机编织过程，结合碳纳米线传感器在拉伸下的电阻变化，利用数学统计评估理论研究三维编织复合材料制件结构的损伤定位和评估算法。

工业大学开发的计算机控制的三维编织复合材料矩形编织机行列数为:180×120，根据三维编织工艺理论，在对应的行列位置上装有位置检测FESTO汽阀，汽阀根据工艺文件由计算机控制实现开启与闭合，完成编织过程。

嵌入碳纳米线传感器时，把编织机的分为4行2列的形式。如图6所示。每个行的碳纳米线电阻变化可以用图7的电路来测量。

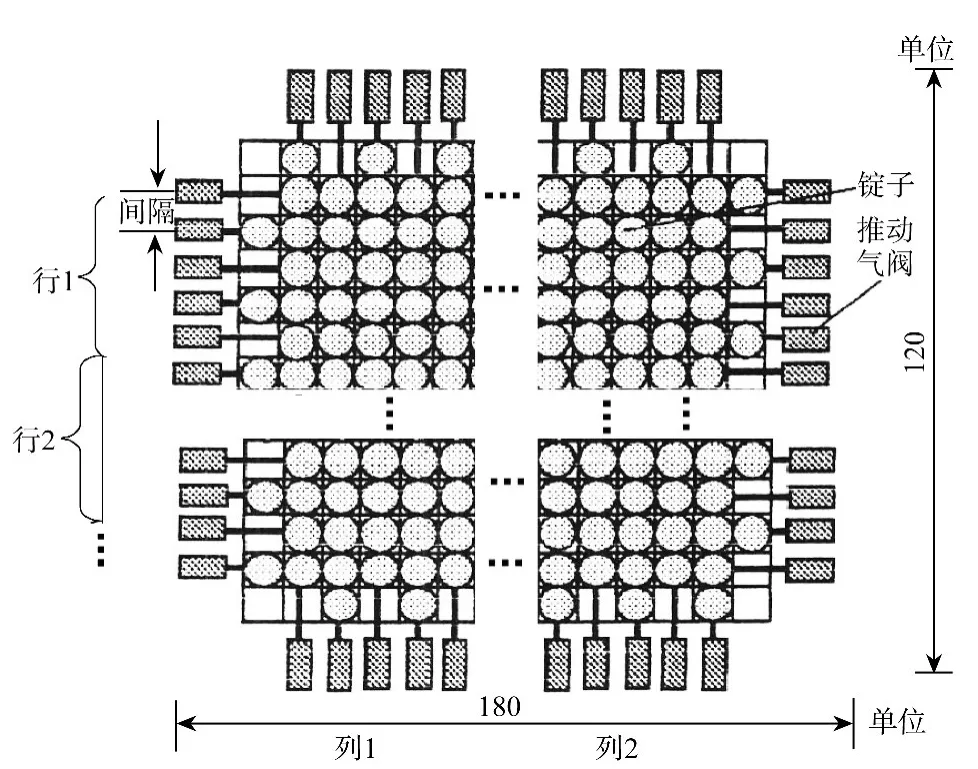
图6 三维矩形编织机底盘结构示意图Fig.6 Structure schematic diagram of chassis for 3-D rectangular braiding machine

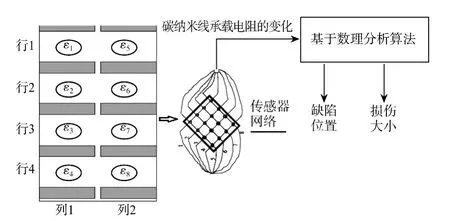
图7 基于数理统计的复合材料缺陷检测算法Fig.7 The algorithm of defect detection for composite material based on mathematical statistics

反应曲面法算法可用一阶回归模型表示为［14］:

如果系统中有非线性，则必须利用较高阶的多项式，如二阶模型:

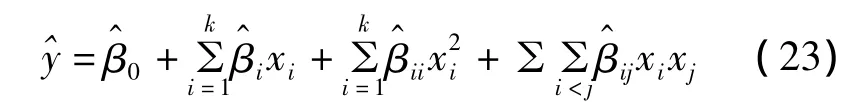
系统采集数据后以最小平方法配适，以寻找出一个适当近似的函数，采用回归分析的显著性检定来检验独立变量与反应变量间的关系强弱，当实验区域接近最佳反应值附近时，则考虑二阶模型。

对于二次多项式的情况下，在图6所示中，在每一行中，有8个电阻值的变化，利用响应表面理论来估计损伤位置(行X，列Y)和尺寸(S)如下:

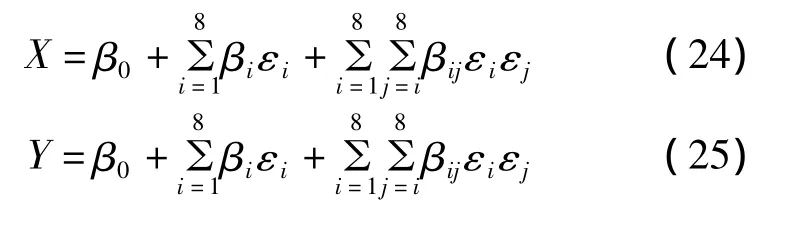
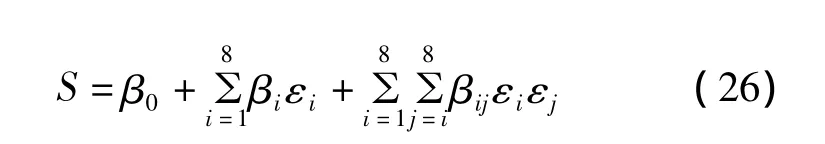
其中，βi(i=0～8)和 βij(i=1～8;j=1～8)为回归系数，所有的回归系数由最小平方误差方法获得的。

系统为提高系统检测的显著性，对采集的数据进行数据归一化处理。

所测量的电阻值的变化可以被看作是8个元素中的一个向量:εi(i=1～8)。矢量的长度η被定义，如下所示:

所有的元素都通过η分频以获得归一化的电阻变化的矢量(V)如下:

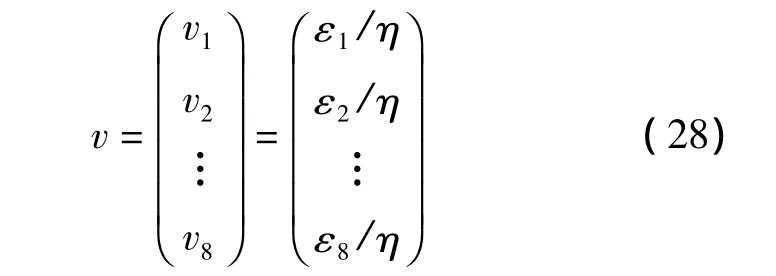
用归一化的电阻值，通过响应表面估计理论计算损伤位置的X和Y:

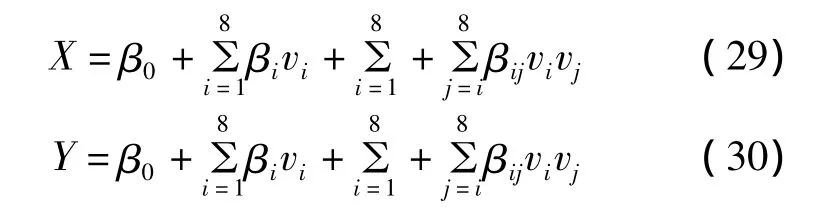
对于损伤尺寸大小(S)的估计是通过电阻矢量的长度的显著性实现，通过每个传感器电阻变化的显著性水平，可以描述损伤尺寸大小:

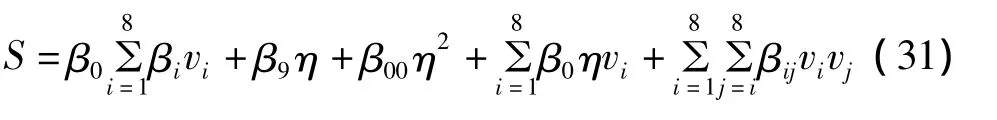
4 实验研究与分析

论文采用三维编织复合材料四步法将直径10μm碳纳米线按不同间距和碳纤维一起编织，试验使用3K碳纤维为T300B、基体为环氧树脂TDE－86、固化剂为70酸酐增强的三维编织复合材料矩形试件，预制件采用四向1×1四步法三维编织结构，采用RTM(树脂传递模塑)工艺复合固化成型。在制成含碳纳米线的三维编织复合材料制件后，将碳纳米线的两端涂抹银胶，试样宽长为25mm×250mm，每个样本的两个碳纳米线端点标记用银胶覆盖并连接两个导线连接器。

应变传感特性实验系统采用日本岛津伺服液压电子拉力机AG－250KNE型万能材料试验机来记录拉力和位移数据，加载速度为1.0mm/min，参数如表1所示。

表1 四步法预制件参数Table 1 The parameters of preform made by four steps method

为分析碳纳米线嵌入三维编织复合材料后力学特性，在4组制件中各取1个试件进行拉伸试验，拉伸电阻－拉伸图如图8所示。

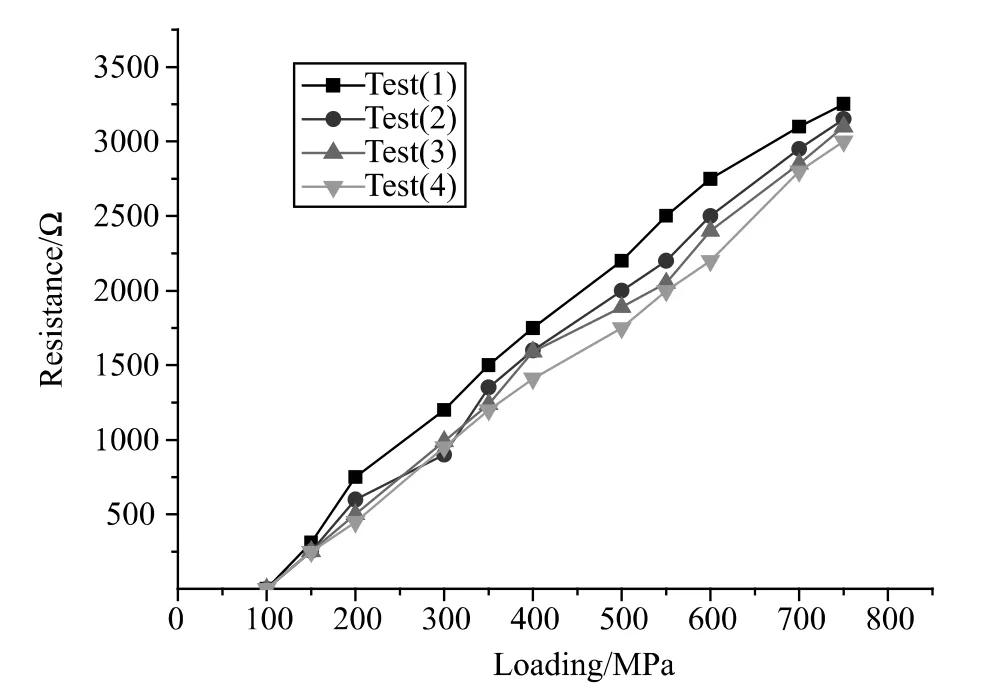
图8 三维编织复合材料拉伸电阻－拉伸图Fig.8 The chart of tensile resistance-loading of three-dimensional braided composites

图8表明三维编织复合材料预制件的编织角对嵌入碳纳米线传感器有一定影响，编织角较小时，在制件拉伸承载中，其电阻变化具有非线性关系。当编织角超过25°时，嵌入预制件的碳纳米线传感器其电阻变化出现了较好的线性关系。

为测量三维编织复合材料内部缺陷，选取第1组的样本进行试验，样本如图9所示。利用扫描电镜(SEM)对图9试件进行检测，图10为制件内部缺陷图。

图9 三维编织复合材料试件图Fig.9 3-D braided composite material specimen

图10 制件1内部SEM缺陷图Fig.10 SEM micrograph of the interior of braided composites

对图9试件进行拉伸试验，检测编织机行位置为1－35。得到如图11所示的电阻变化图，在图11中纵坐标为碳纳米线的电阻变化，横坐标为碳纳线传感器所在的编织机行位置。

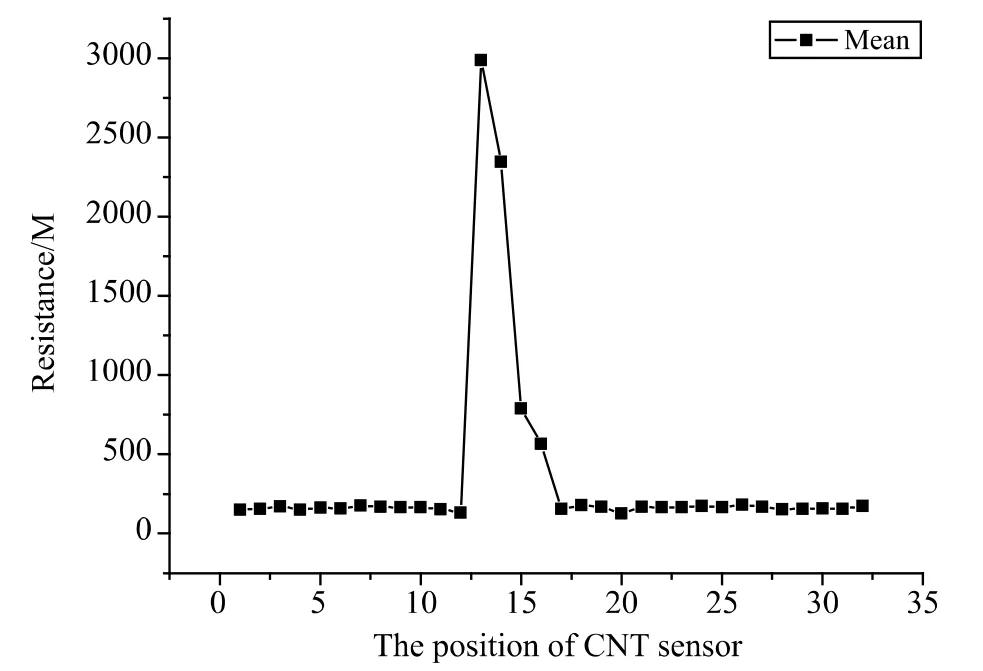
图11 碳纳线传感器电阻变化(行1－35)Fig.11 Variation of resistance of carbon nanotube thread sensor(row 1－35)

图12所示为碳纳米线传感器在编织机列位置的电阻变化图。

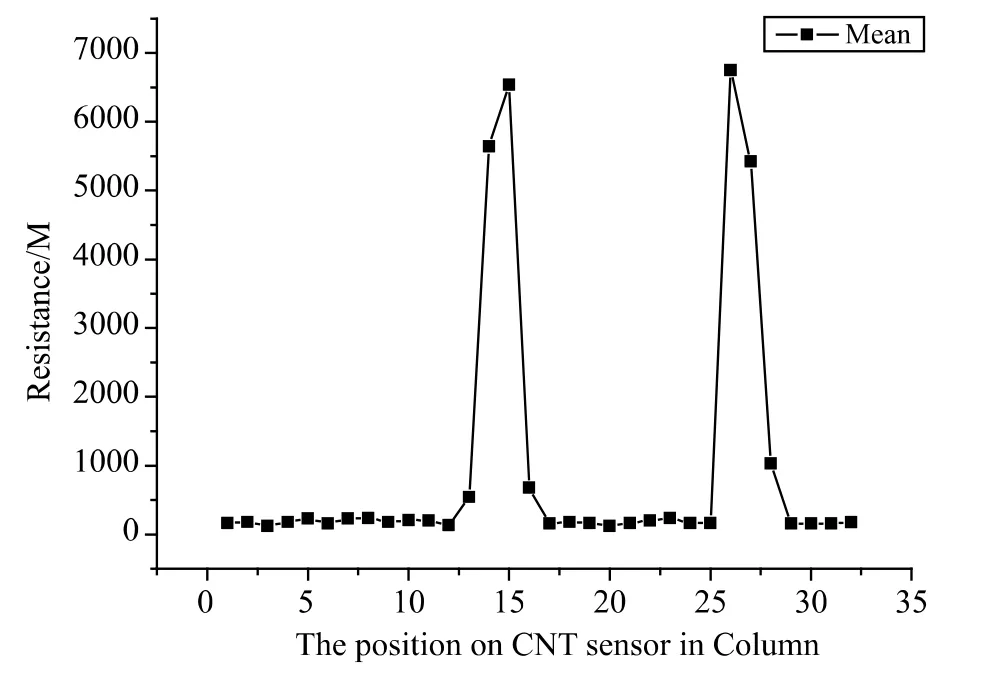
图12 碳纳米线传感器列位置电阻变化(列1－35)Fig.12 Variation of resistance of carbon nanotube thread sensor(column 1－35)

利用响应表面估计理论计算损伤位置得到表2结果。

表2 系统检测结果Table 2 Test results

由表2看出，所检测的结果与图10所示的结果一致，特别是在图10很小的缺陷，碳纳米线传感器均能检测出。这表明碳纳米传感器在复合材料预制件中，能准确反映制件承载过程中电阻的变化。

应用X2测试，进行分布的适合性的检验，根据X2分布，y0来自以下公式:

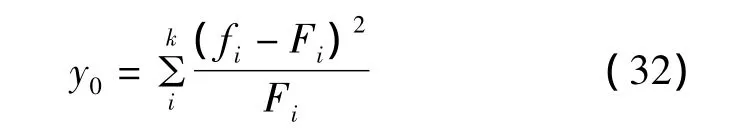
其中，k是离散分布的类的数量，fi是每个类别中包含的样本大小，Fi是由理论分布推导出的预期大小。由于Fi必须超过5.0，从实验分布得出的y0值分别为(6.84，8.90，16.2，9.22)。在测试中，5%的临界值是=1.97。由于y0不超过临界值时，所以估计误差的每个分布服从正态分布。估计的剩余误差服从正态分布，估计的误差范围是从正态分布的99%置信区间计算得到的。裂纹的误差范围x方向上是2.4μm，y方向上是1.8μm。

图13和图14所示，依据公式(29)和(30)计算的估计的误差范围。图13、图14中，实线是本方法的标准偏差的概率分布估计，虚线是T分布误差分布。误差范围是由估计误差的标准差和99%的置信区间决定的。可以看出X2估计的误差范围比T分布的要小。从这些结果，我们可以得出结论，采用不同的估计方法对测量误差有一定影响。

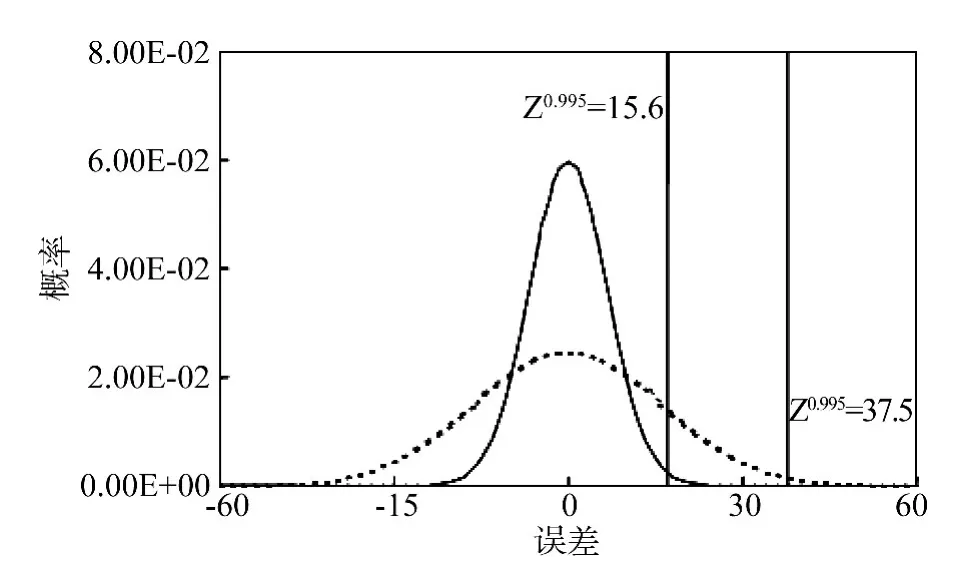
图13 X方向残留误差的估计Fig.13 Residual error of estimation in X direction

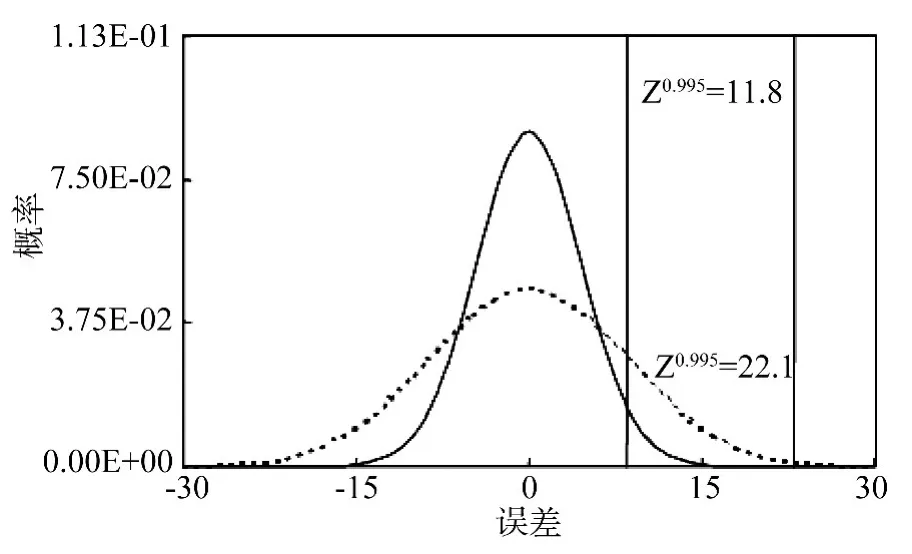
图14 Y方向残留误差的估计Fig.14 Residual error of estimation in Y direction

5 结论

(1)碳纳米线传感器应用于三维编织复合材料试件健康监测较其它传感器具有容易嵌入的优点，碳纳米管在承载过程中，具有较好的线性，嵌入碳纳米管传感器的三维编织复合材料试件对力学性能影响很小。

(2)在本研究中，使用电阻变化的方法与反应表面理论分析复合材料的内部缺陷是可行的，它可以对缺陷大小和位置进行识别。

(3)采用不同的估计方法对测量误差有一定影响，估计的误差范围比T分布的方法要小。

［1］Li W Hammad，EI-Shiekh A.Structural analysis of 3-D braided preforms for composites，partⅠ:The four-step，preform ［J］.J.Text Inst，1990，81(40):515－537.

［2］赵晖.天津工大复合材料“支”起嫦娥二号［N］天津网－数字报刊，2010－10－13.

［3］WAN Zhenkai，LI Jingdong，Li Jialu.Structural health monitoring(SHM)of three-dimensional braided composite material using carbon nanotube thread sensors［J］.Journal of Mechanics，2013，29(4):617－621.

［4］Jandro L Abot，Mark J Schulz，Yi Song，et al.Novel distributed strain sensing in polymeric materials［J］.Smart Mater.Struct.，2010，19(8):85007－85018.

［5］顾钧元，徐廷学，余仁波，等.结构健康监测及其关键技术研究［J］.兵工自动化，2011，30(08):61－64.

［6］万振凯，贡丽英.三维编织复合材料健康监测数据异常诊断研究［J］.材料导报，2013，27(10):74－77.

［7］Chun Yu Li，Tsu Wei Chou.Strain and pressure sensing using single-walled carbon nanotubes［J］.Nanotechnology，2004，15(11):1493 －1496.

［8］Joung-Man Park a d，Sung-Ju Kim a，Dong-Jin Yoon b，et al.Self-sensing and interfacial evaluation of Ni nanowire/polymer composites using electro-micromechanical technique［J］.Composites Science and Technology，2007，67:2121 －2134.

［9］N.D.Alexopoulos a b，C.Bartholome c，P.Poulin c，et al.Damage detection of glass fiber reinforced composites using embedded PVA－carbon nanotube(CNT)fibers［J］.Composites Science and Technology，2010，70:1733 －1741.

［10］Haibo Zhao，Yingying Zhang，Philip D Bradford，et al.Carbon nanotube yarn strain sensors［J］.Nanotechnology，2010，21:305502 －305507.

［11］Z.Wan，J.D.Li，M.Jia.Structural health monitoring(SHM)of three-dimensional braided composite material using carbon canotube thread sensors［J］.Journal of Mechanics，2013，29(4):616－621.

［12］微型系统智能复合材料连续健康监测［EB/OL］.http:∥www.frponline.com.cn/news/detail_33195.html.

［13］李静东，李嘉禄，万振凯.基于碳纳米线的三维编织复合材料健康监测技术［J］.材料导报，2012，26(4)，109 －113.

［14］Iwasaki Atsushi;Todoroki Akira.Statistical evaluation of modified electrical resistance change method for delamination monitoring of CFRP plate［J］.Structural Health Monitoring，2005，4(2):119－136.