面齿轮磨削温度建模仿真与分析

肖 磊，明兴祖，刘金华，高 钦，龙 誉

（湖南工业大学 机械工程学院，湖南 株洲 412007）

面齿轮磨削温度建模仿真与分析

肖 磊，明兴祖，刘金华，高 钦，龙 誉

（湖南工业大学 机械工程学院，湖南 株洲 412007）

根据椭圆接触理论，得出碟形砂轮磨削面齿轮时的基本磨削参数，并建立了有限元模型，采用矩形分布热源对面齿轮磨削热进行模拟，得出其磨削温度场。由该模拟结果得出碟形砂轮磨削时的温度变化规律为：沿齿长方向近心端和沿齿高方向相对接近齿根区域时，面齿轮的磨削温度逐渐升高。同时，利用红外测温仪对实际机齿轮磨削温度进行测量，将所得结果与有限元分析结果进行对比，发现各磨削点的误差分析结果均在5%～20%，并且温度越高，误差越小，从而验证了椭圆接触理论在面齿轮磨削热研究中的可行性。

椭圆接触理论；面齿轮磨削；温度场点磨削；有限元仿真

0 引言

面齿轮是一种新型的齿轮传动方式，具有承载能力强、结构紧凑、质量轻、互换性高、安装调试简易、传动振动与噪声小、动力分流效果好等优点[1]。现已被广泛应用于交通、国防和各种高端设备传动等领域中[2]。而为了能保证其传动作用得到更好的应用，对面齿轮的磨削技术水平提出了越来越高的要求。

面齿轮磨削技术主要是对磨齿齿面的加工，加工后的齿轮表面性能决定着齿轮的实用功能性。对面齿轮齿面进行磨削的过程中，温度是反映其磨削过程质量的一个重要指标。到目前为止，有许多科研工作者为磨削温度场的研究提供了大量的宝贵资料。最早的是J. C. Jaeger[3]提出的矩形热源理论，这是温度场分析最基础的研究单元；之后，贝季瑶[4]提出了三角形热源模型，丰富了研究单元的类型；随后，孟国庆等[5]推出了一维、二维导热模型的磨削温度解析式，并且在此基础上计算出了干磨和湿磨状态下磨削温度场的解析式，这对面齿轮的温度研究做出了重大的理论突破。

目前，国内外对于面齿轮高速磨削方面都有一定的研究，但对于面齿轮数控磨齿温度场[6]的具体研究分析却未见报道。因此，本文以Gleason接触原理在面齿轮碟形砂轮磨削中的应用作为理论依据[7]，应用椭圆接触理论，并且选用格里森技术，根据局部共轭原理[8]得到面齿轮的磨削基本参数；同时，对碟形砂轮磨削面齿轮时的磨削温度场进行理论分析与仿真[9]，以证明椭圆接触理论应用的正确性。最后，通过磨削温度试验[10]对温度场的仿真进行了证明，为进一步研究面齿轮温度场和应力应变场提供一定的理论参考。

1 椭圆接触理论

由面齿轮蝶形砂轮磨削原理可知，蝶形砂轮在磨削过程中与面齿轮的接触方式为点接触磨削，从而可由Gleason接触原理得出砂轮磨削接触点瞬时接触为椭圆接触。因此，可通过椭圆上的各个参数点的计算来表示两接触齿面上的各个参数数据。砂轮磨削接触点瞬时接触椭圆如图1所示，它以椭圆的中心为磨削点，椭圆长半轴a、短半轴b分别为面齿轮磨削接触弧长和磨削接触宽度。

图1 瞬时接触椭圆Fig. 1 The instant contact ellipse

1.1 主曲率与主方向夹角的计算

根据微分几何与齿轮啮合原理[11]，可设齿面方程为r = r(x, y, )。根据曲面论可知，光滑曲面的基本几何量为第一基本二次型和第二基本二次型，这是计算面齿轮磨削时的主曲率与主方向夹角的基础，所以可先求出其主曲率。

曲面在任意一点处的弯曲程度，可以用曲面在此点临近处离开曲面切平面的程度来衡量。所以在曲面上任意一点，其各个方向的法曲率不同，本研究取它的2个极值点作为该点的主曲率。

曲面上任意一点的法曲率公式如下：

再由向量夹角公式，可求得主方向的夹角。

1.2 接触椭圆方程的建立

面齿轮磨削加工过程中，可通过磨削力引起的齿面接触弹性变形量、磨削深度及齿轮接触时的弹性变形量，确定蝶形砂轮磨削时的瞬时接触椭圆方程[12]。本研究中两齿面的接触椭圆如图2所示。

图2 两齿面的接触椭圆Fig. 2 Two tooth contact ellipse

由此可以得出椭圆长半轴a、短半轴b的计算公式如下：

式（8）中：ap为磨削深度；

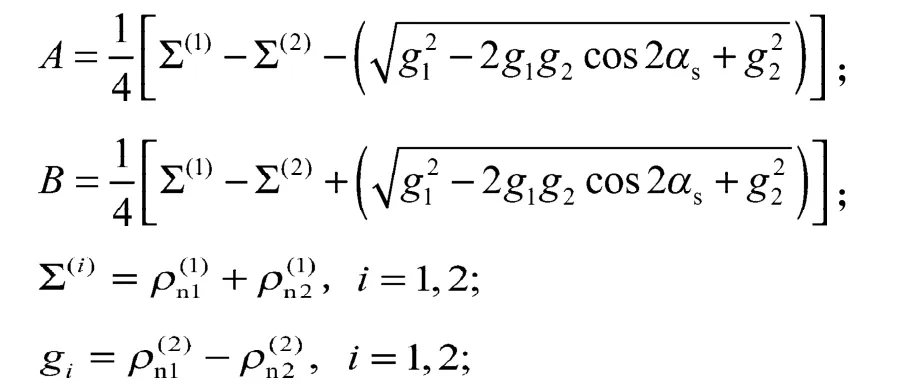
2 磨削基本参数

磨削基本参数主要包括磨削切向力、磨削热流密度和接触弧长。

2.1 磨削切向力

磨削切向力Ft可由式（9）所示经验公式[13]得出：

式（9）中：Fp为单位磨削力；

bd为磨削加工宽度；

2.2 磨削热流密度

运用JAEGER热源理论，可知在面齿轮磨削热载荷分析中，采用呈矩形分布的热源比呈三角形分布的热源更有利于试验的进一步分析与计算。因此，可以据此计算出其移动式热源在磨削过程中的热流密度q，其计算公式为

式（10）中：b*为理论接触宽度；

vw为展成速度；

vs为砂轮切向速度；

Rw为输入工件的热量分配比例，其中，水基磨削液的Rw为0.65；

lk为磨削接触弧长。

3 磨削温度场有限元仿真分析及其试验验证

3.1 磨削温度场有限元仿真分析

本文所采用的面齿轮模型仿真参数见表1。

表1 正交面齿轮主要参数Table 1 Main parameters of orthogonal face gear

面齿轮的材料为18Cr2Ni4WA，其在磨削温度场的工艺参数如表2所示，且采用水基磨削液逆磨。

表2 面齿轮磨削温度场工艺参数Table 2 Grinding temperature field parameters of orthogonal face gear

根据旋转投影面齿面网络沿齿长方向进行九等分、齿高方向五等分，对得到的45个交点进行测温试验。由于面齿轮齿面形状复杂，同时磨削参数（如磨削接触弧长、热流密度、磨削宽度等）在每个点的位置都不相同，所以选取具有代表性的5个点进行分析[14]，选取的测温点如图3所示。

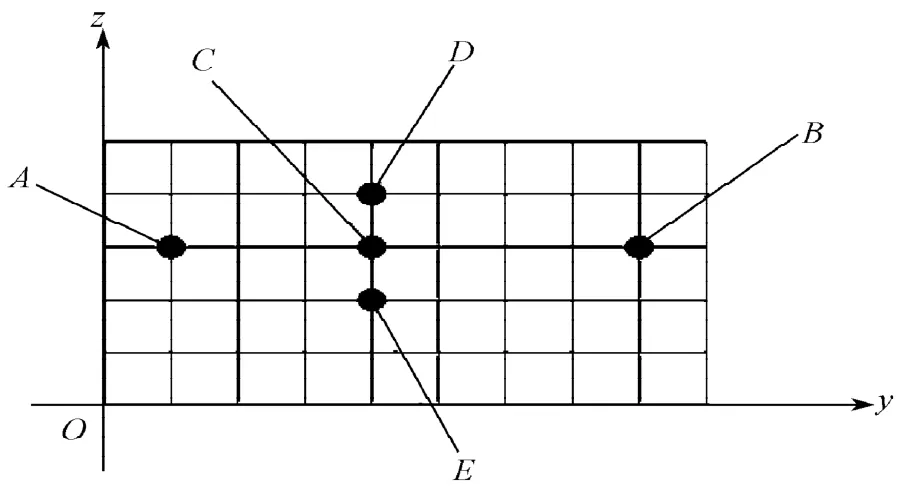
图3 测温点分布示意图Fig. 3 Schematic diagram of temperature measurement points

下面以A点为例描述其计算过程与结果。

根据公式（8）可得：

磨削接触弧长lk=a=0.668 2 mm；

磨削宽度be=b=0.522 4 mm。

由干磨式热量分配系数计算公式可知，磨削区的热量分配系数为：

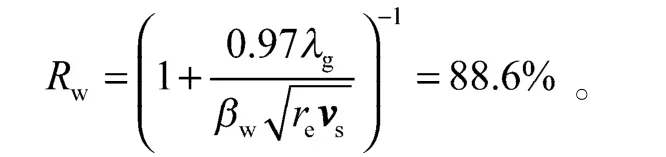
re为磨粒接触有效半径。

为了使仿真模型简化后不影响后续结果，做出以下假设：

1）工件材料各向同性，且其属性不随温度的改变而发生变化；

2）不考虑碟形砂轮在磨削过程中的磨损；

3）磨削过程中不考虑辐射。

通过面齿轮的插齿原理，并利用Matlab编程，得到面齿轮的齿面方程，再将其导入proe生成面齿轮模型，然后将其igs文件导入Ansys软件中进行有限元分析。Ansys软件中需要进行如下参数设定：设定瞬态温度分析，设定初始条件，定义材料属性，加载热约束条件和热载荷大小及载荷步。利用磨削接触弧长lk得到q的加载时间，t=lk/vw=0.003 4 s；同时，为了方便后续分析与计算，取每个载荷步时间为0.000 68 s，分5步进行。由公式计算，可以得出磨削时产生的热流量的大小。注意施加热流量载荷时，应将其加载在磨削时的等效中心节点上进行模拟分析，并且在面齿轮的几个选取点分别进行干磨分析。经过求解，得到如图4所示的有限元分析模型。

图4 面齿轮的有限元分析模型Fig. 4 The finite element analytical model of orthogonal face gear

因为本研究中主要分析其中一个面的温度变化情况，所以对于单个面齿轮轮齿的模型采用整体自由网格划分，并对要进行磨削温度分析的齿面进行参数为0.2的密化。以此获取较高的精度解，同时可减少运算量。

经求解后，得到了各测试点的磨削温度场，具体如图5所示。

图5 不同磨削点磨削温度场云图Fig. 5 Cloud chart of grinding temperature fields of different grinding points

在碟形砂轮磨削面齿轮时，采取干磨方式，在vw=1 m/min，ap=0.02 mm，vs=20.6 m/s的磨削工艺参数条件下，求解得到各点的齿面最高温度分别如下：A点为122.827 ℃，B点为321.161 ℃，C点为297.926 ℃，D点为220.398 ℃，E点为317.784 ℃。各最高温度均处于磨削热源的中心区域[15]，这与矩形热源分布的规律相吻合。所选取的各磨削点的具体温升变化情况如图6所示。

图6 面齿轮A～E各点最大温度曲线图Fig. 6 The maximum temperature curves of each point A～E

由图6可以看出，面齿轮各磨削点处的温度均随着时间的延长而增大。这是由于：在极短的时间内，砂轮与齿轮磨削区域接触所产生的热量非常大，热量来不及散开而堆积在齿轮表面，所以齿轮表面的磨削温度很高。另一方面，由于点磨削最先开始的是划擦和耕犁阶段，其中主要发生的是弹性变形，所以温度上升的趋势比较明显，而后半段则是产生大量磨削的过程，在磨削的过程中，磨削带走了大部分热量，所以温度变化较为平缓。

对齿长方向的A,B,C点的磨削温度进行比较，结果如图7所示。

图7 沿齿长方向的磨削点温度变化Fig. 7 Grinding point temperature changing along the tooth length

由图7可知，磨削点B的升温速率明显比点A快，这是由于在近心端，齿面曲率降低，导致椭圆接触面积增大，因而导入工件的热量上升。通过对磨削点A, B, C的分析可知，面齿轮沿齿长方向的磨削温度为整体上升趋势，从磨削点A到磨削点C，曲率的变化比较大，所以显示出上升幅度比较快，而从磨削点C到点B的过程中，其面齿轮齿面曲率变化趋于平缓，说明磨削温升比较慢。

对齿高方向的磨削点D, C, E的磨削温度进行比对分析，结果如图8所示。

图8 沿齿高方向的磨削点温度变化Fig. 8 Grinding point temperature changing along the tooth height

由图8可知，通过对磨削点D, C, E的对比分析，在面齿轮沿齿高方向的磨削温度整体呈上升趋势，磨削点E的升温速率明显比点D快，这是由于在齿根处，齿面曲率降低，从而导致椭圆接触面积增大，导入工件的热量上升。

同时，对比齿长方向的温度变化可以发现，由于齿高方向的齿面曲率变化比较小，所以沿齿高方向的温度变化没有沿齿长方向的变化明显。

3.2 磨削温度试验验证

本研究使用型号为SCIT-3（包含一个XST仪表，一个测头，CIT-3AXXT）的低温红外测温仪测量面齿轮的磨削温度，测量距离系数为15:1，测量范围为0～500 ℃。该仪表的工作原理如图9所示。

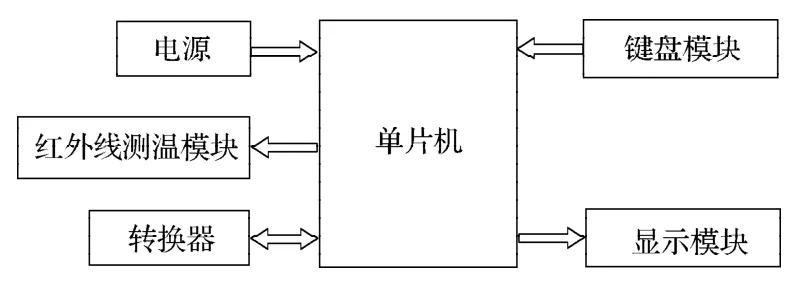
图9 红外测温仪表结构图Fig. 9 Structure diagram of infrared thermometer

面齿轮磨削温度测试的基本流程如图10所示。

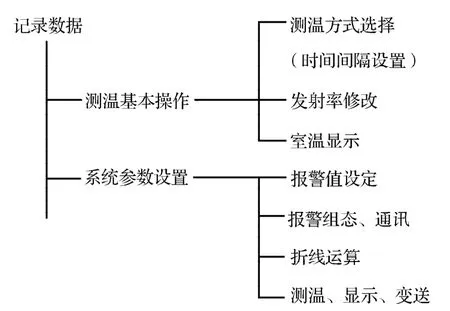
图10 测温流程Fig.10 Temperature measurement process

测量所得各点磨削温度结果见表3中的实测值。

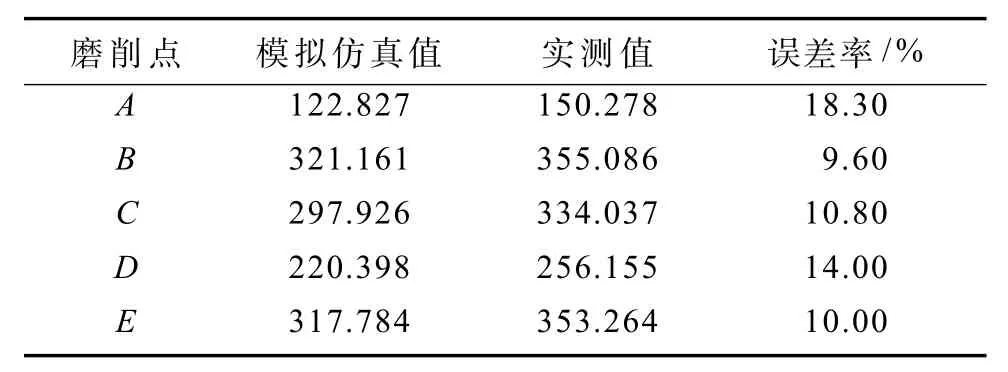
表3 温度数据对比Table 3 Temperature data comparison chart

分析表3中的数据可知，各磨削点的误差分析结果均在5%～20%之间，这是由于蝶形砂轮与面齿轮是相对运动的，在工件表面会产生大量热量，所以造成实际得到的测量温度比Ansys有限元分析结果稍高；同时，温度越高，误差越小，这是由红外测温仪的波长反馈更为准确造成的。

由于面齿轮建模齿面是个很复杂的曲面，其曲面上各个点的参数不一样，所以磨削时的情况都不同。当需要在其表面施加移动载荷时，会存在一定的误差，而采用椭圆接触理论可为分析磨削面齿轮方面提供参考。

4 结论

本文对面齿轮的磨削温度场进行了Ansys有限元模拟仿真分析，但对于其移动热载的施加未进行分析，只对于在同一齿面上的同齿高和同半径的矩形热源进行了有限元分析，得出如下结论：

1）由面齿轮温度场有限元分析结果可以得知，碟形砂轮每个磨削点的接触面积和热流密度都不相同，其整体趋势可视为定义为沿齿长方向近心端时，瞬时椭圆接触面积增加，相应的磨削温度较高；沿齿高方向，相对接近齿根区域，随着椭圆接触面积的增加，磨削温度升高；而热流密度的大小变化规律恰好与其相反。

2）对面齿轮蝶形砂轮磨削有限元分析中，面齿轮在蝶形砂轮磨削时为接触面积小的点磨削，磨削温度不是很高，但是在整体磨削过程中，每个点的磨削所产生的热量不同，因此在面齿轮磨削过程中，齿面的金相组织变化不同。

3）红外测温仪对实际磨削温度的测量结果表明，各磨削点的测量结果与有限元分析结果的误差均在5%～20%间，并且温度越高，误差越小。这一结果验证了椭圆接触理论在面齿轮磨削热研究中的可行性。

本研究结论为进一步实现碟形砂轮磨削和提高面齿轮的磨削效率提供了一定的理论基础。

[1]吴晓铃，袁丽娟，徐万里. 中国齿轮传动的历史与进展[J]. 机械传动，2004，28(5)：62-64. Wu Xiaoling，Yuan Lijuan，Xu Wanli. The History and Development of Gear Technology of China[J]. Journal of Mechanical Transmission，2004，28(5)：62-64.

[2]Litvin F L，Wang J C, Bossler R B. Application of Face-Gear Drives in Helicopter Transmissions[J]. Journal of Mechanical Design, Transactions of the ASME, 1994，116 (3)：672-676.

[3]Jaeger J C. Mowing Sources of Heat and the Temperature at Sliding Contacts[J]. Proceedings of Royal Society of New South Wales，1942，76：203-224.

[4]贝季瑶. 磨削温度的分析与研究[J]. 上海交通大学学报，1964(3)：55-71. Bei Jiyao. Analysis and Research of Grinding Temperature[J]. Journal of Shanghai Jiaotong University，1964(3)：55-71.

[5]孟国庆，李文卓. 磨削温度场的数值计算[J]. 现代制造工程，1996(10)：25-27. Meng Guoqing. Li Wenzhuo. Numerical Calculation of Grinding Temperature Field[J]. Modern Manufacturing Engineering，1996(10)：25-27.

[6]王胜伟，何 瑛，何国旗，等. 面齿轮啮合轮齿本体温度场影响因素的仿真分析[J]. 湖南工业大学学报， 2014，28(5)：43-49. Wang Shengwei，He Ying，He Guoqi，et al. Simulation Analysis of the Influencing Factors on Face-Gear Tooth Bulk Temperature in Meshing Process[J]. Journal of Hunan University of Technology，2014，28(5)：43-49.

[7]Michele Guingand，Jean-Pierre de Vaujany，Colin-Yann Jacquin. Quasi-Static Analysis of a Face Gear Under Torque [J]. Computer Methods in Applied Mechanics and Engineering，2005，194(39/41)：1-8.

[8]Stardtfeld H J. Handbook of Bevel and Hypoid Gears[M]. New York： Rochester Institute of Technology，1993：190-200.

[9]彭先龙，方宗德，苏进展，等. 采用碟形砂轮的面齿轮磨齿方法理论分析[J]. 航空动力学报，2012，27(5)：1159-1165. Peng Xianlong， Fang Zongde，Su Jinzhan，et al. Theory Analysis for Application Grinding Disk in Face Gear Grinding [J]. Journal of Aerospace Power，2012，27(5)：1159-1165.

[10]尤芳怡，徐西鹏. 红外测温技术及其在磨削温度测量中的应用[J]. 华侨大学学报 ：自然科学版，2005，26(4)：338-342. You Fangyi，Xu Xipeng. Applications of Infrared Technique in the Measurement of Grinding Temperatures [J]. Journal of Huaqiao University：Natural Science，2005，26(4)：338-342.

[11]傅则绍. 微分几何与齿轮啮合原理[M]. 东营：石油大学出版社，1999：26-63. Fu Zeshao. Differential Geometry and Meshing Theory of Gears[M]. Dongying：China University of Petroleum Press，1999：26-63.

[12]赵 磊，明兴祖，王 伟，等. 基于Matlab的正交面齿轮设计及可视化分析[J]. 湖南工业大学学报，2014，28 (5)：38-42. Zhao Lei，Ming Xingzu，Wang Wei，et al. Matlab-Based Orthogonal Face-Gear Design and Visualization Analysis [J]. Journal of Hunan University of Technology，2014，28(5) ：38-42.

[13]刘艳平. 直齿-面齿轮加载接触分析及弯曲应力和接触应力计算方法研究[D]. 长沙：中南大学，2012. Liu Yanping. Straight Teeth - Face Gear Loaded Contact Analysis and Bending Stress and Contact Stress Calculation Method Research[D]. Changsha：Central South University，2012.

[14]周里群，邱 奕，吴义彬，等. Cr18Mn18N奥氏体不锈钢磨削过程温度场及热应力耦合的有限元模拟[J]. 机械工程材料，2014，38(4)：96-99. Zhou Liqun，Qiu Yi，Wu Yibin，et al. FEM Simulation of Temperature Field and Thermal Stress Coupling in Grinding for Cr18Mn18N Austenitic Stainless Steel[J]. Materials for Mechanical Engineering，2014，38(4)：96-99.

[15]聂少武. “奥”制准双曲面齿轮的加工调整计算与齿面误差测量[D]. 洛阳：河南科技大学，2009. Nie Shaowu. Machining Adjustment Calculation and Tooth Surface Error Measurement on Austenitic Quasi Hyperbolic Gear[D]. Luoyang：Henan University of Science and Technology，2009.

（责任编辑：廖友媛）

Modeling and Analysis of Face-Gear Grinding Temperature

Xiao Lei， Ming Xingzu， Liu Jinhua， Gao Qin， Long Yu
（School of Mechanical Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China）

According to the elliptical contact theory , obtained disc wheel basic grinding parameters of gear grinding surface and established finite element model, and using the rectangular distribution of heat for the gear grinding thermal simulation, obtained the grinding temperature field. The results showed that the temperature variation law of the saucer wheel grinding is : along the direction of tooth proximal near heart and along the direction of tooth height relatively close to the root area, the grinding temperature gradually increased. Meanwhile using infrared thermometer to measure actual grinding temperature, compared the measured temperatures with the finite elemental analysis results, found that the error analysis results of all the grinding points were between 20% and 5%, and the higher the temperature, the smaller the error was, verified the feasibility of the ellipse contact theory in the surface gear grinding thermal research.

the elliptical contact theory ；face gear grinding ；point grinding temperature field ；finite element simulation

TH132. 41

A

1673-9833(2015)05-0034-06

10.3969/j.issn.1673-9833.2015.05.008

2015-07-09

国家自然科学基金资助项目（51375161），湖南省自然科学基金资助项目（2015JJ5018）

肖 磊（1990-），男，湖北荆州人，湖南工业大学硕士生，主要研究方向为数字化制造理论与技术，E-mail：852625057@qq.com