银膜表面等离子体耦合辐射特性的仿真分析

陈 晨 逯丹凤 程 进 祁志美,,*(中国科学院电子学研究所, 传感技术国家重点实验室, 北京 0090;国民核生化灾害防护国家重点实验室, 北京 005)

银膜表面等离子体耦合辐射特性的仿真分析

陈 晨1逯丹凤1程 进1祁志美1,2,*
(1中国科学院电子学研究所, 传感技术国家重点实验室, 北京 100190;2国民核生化灾害防护国家重点实验室, 北京 102205)

表面等离子体耦合辐射(SPCE)是传统表面等离子体共振(SPR)的逆过程: 当分子足够靠近金属薄膜表面时(< 200 nm), 其受激辐射的能量可以耦合成SPR模式并定向辐射到棱镜中. 由于具有场增强特性、高收集效率和优异的表面选择性, SPCE作为一种新的表面分析技术已经在荧光和拉曼光谱领域得到了有效的应用.本文采用光学互易定理简化传统SPCE的计算方法. 通过计算, 我们得到了SPCE一维和二维辐射功率密度分布, 表面选择性, 辐射角的波长色散特性, 辐射角半峰宽与银膜厚度的关系. 仿真结果与已报到的实验结果吻合良好, 验证了该方法的有效性.

表面等离子体耦合辐射; 光学互易定理; 表面等离子体共振; 荧光光谱学; 拉曼光谱学

1 引 言

荧光光谱和拉曼光谱在化学和生物领域都是非常重要的研究方法.1–4为了探测痕量物质甚至单分子, 研究者们一直致力于提高荧光和拉曼光谱技术的检测灵敏度. 最常用的提高灵敏度的方法是提高目标分子所在区域的光电场强度. 在入射光功率不变的情况下通常依赖于局域表面等离子体共振效应(LSPR). 基于LSPR的表面增强拉曼散射技术(SERS)已经极大地推进了拉曼光谱技术的发展, 而亚波长量级的纳米结构也被用来提高荧光分子的荧光强度、量子产率和光学稳定性.5–10然而, LSPR效应极大地依赖于增强基底的纳米结构, 而制备复杂纳米结构工艺较为繁琐并且重复性不佳. 提高灵敏度的另一种方法则是控制散射光信号的空间分布从而提高信号的收集效率.11–15表面等离子体耦合辐射(SPCE)方法就是通过限制辐射方向, 从而提高信号的收集效率.16–18

SPCE的激发方式有两种: 体光束激发方式和SPR激发方式. 体光束激发方式即直接用激光照射金属薄膜表面附近的分子. 这种激发方式实现较为简单, 但是缺乏场增强机制. SPR激发方式是指从棱镜一侧首先激发SPR模式, 通过SPR产生的增强消逝场去激发金属薄膜表面附近的分子. SPR激发方式由于具有一些突出的优点从而得到了更广泛的关注. 首先, SPR激发方式使得金属表面电场相对入射电场得到显著的增强, 从而可以得到更强的散射信号; 其次, 相对于粗糙金属表面的LSPR效应, 平滑金属表面SPR效应的场增强因子可以得到更精确的计算和控制, 从而使得检测灵敏度可控, 重复性更好; 最后, 由于SPR消逝场是横向磁场(TM)偏振的,因此通过检测散射信号的峰位可以估算分子的取向.19,20考虑受激分子的辐射过程, 由于很大一部分辐射功率被耦合成SPR模式并被定向辐射到棱镜中, 因此利用SPCE方法可以得到更高的收集效率.根据实验结果, 大约50%的荧光信号可以从棱镜一侧被收集到, 远高于普通的激发-收集方式(收集效率约1%).21分子散射信号与SPR模式的耦合效率随分子-金属薄膜之间的距离增大而快速减小, 这意味着来自于远离金属薄膜表面的分子的散射信号不能被定向辐射到棱镜中, 因此SPCE技术具有优异的表面选择性.

计算电偶极子在分层结构中的辐射分布的经典方法是将辐射场分解为平面波的叠加, 即空间上的二维傅里叶变换, 然后再用菲涅尔理论计算沿不同方向传播的平面波的透射和反射.17这种计算方法比较复杂. 本文通过应用光学互易定理简化了计算过程. 通过计算, 我们得到了SPCE的一维和二维的辐射功率密度分布、表面选择性、波长色散特性、辐射半峰宽与银膜厚度的关系. 仿真结果与已报到的实验结果吻合得很好, 验证了该方法的有效性.

2 SPCE计算方法

如图1(a)所示, 光学互易定理指出, 在Q1点沿e1方向振动的电偶极子p1= p1e1在Q2点产生的电场E1与一个在Q2点沿e2方向振动的电偶极子p2= p2e2在Q1点产生的电场E2之间有如下关系:22–24

我们总是选取p2与E1具有相同的方向(即e2与r垂直).当Q1点与Q2点之间的距离非常大且两个偶极子之间不存在散射体时, p2在Q1点产生的电场E2可以用一个沿 –r方向传播的平面波在Q1点产生的电场近似:

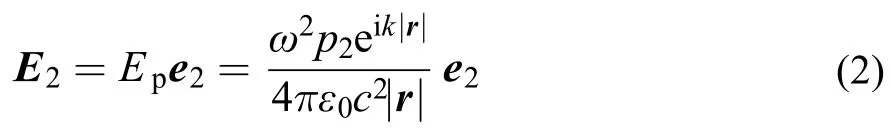
Ep是此近似平面波的振幅, k是平面波的波矢, ε0为真空介电常数, ω为电偏移子角频率.

如图1(b)所示, 当p1位于分层结构中而p2位于棱镜中且两者距离非常大时, 由p2在p1处产生的电场E2可以由平面波Ep在p1处激发的局域电场Eloc代替,再由式(1)和(2)可得:

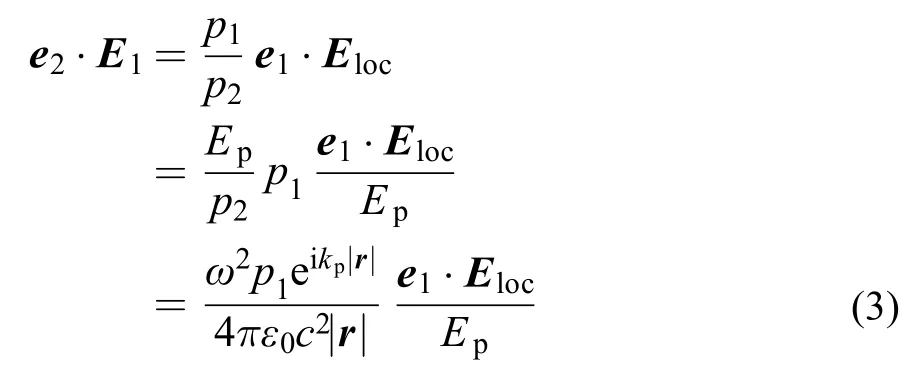
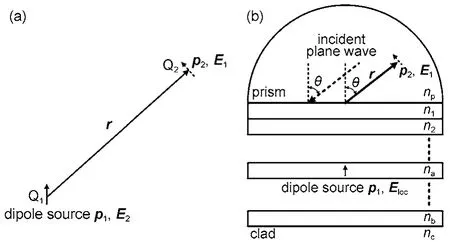
图1 光学互易定理示意图Fig.1 Schematic diagram for explaining the optical reciprocity theorem

kp是平面波在棱镜中的波矢. 由于p2总是取与E1具有相同方向, 并且令EFL= e1Eloc/Ep, 表示分层结构引入导致的局域场增强因子, 则式(3)可简化成:

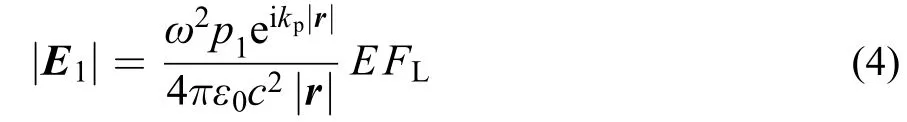
上式即分层结构中的电偶极子p1在远场区域(棱镜中)的辐射电场分布, 使用坡印亭定理可以计算远场时间平均功率密度:25

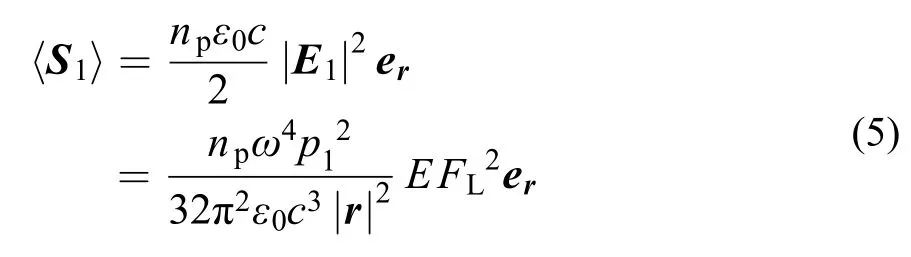
np是棱镜的折射率, er是沿r方向的单位矢量. 使用远场条件|r| = 1 m并取p12= 12πε0c3/ω4使电偶极子在真空中的辐射功率为1 W, 式(5)简化为:

公式(6)说明: 我们只需要求得沿–r方向入射的平面波在电偶极子所在位置对应的局域场增强因子, 就可以求得该电偶极子沿r方向辐射的功率密度. 以上公式包含棱镜折射率np, 用于计算棱镜中的场分布.当求解覆盖层中的场分布时, 只需将各公式中的np改为覆盖层折射率nc即可.

3 SPCE计算结果与讨论

3.1 SPCE结构

计算所用SPCE结构如图2所示.26棱镜表面溅射一层50 nm厚的银膜, 然后在银膜上吸附尼罗兰单分子层. 激发方式可以选择利用激光从棱镜一侧先激SPR模式, 再由SPR消逝场激发银膜表面的尼罗蓝分子. 最终获得的辐射分布与激发方式的选择无关. 在计算中, 吸附分子被简化成单个电偶极子. 由于尼罗蓝分子分子量很小而SPR对小分子不敏感,因此吸附的尼罗蓝单分子层对SPR共振角的影响可以忽略不计. 根据文献,26激发波长选择为647 nm. 尼罗兰分子的典型拉曼峰在590 cm–1, 对应的拉曼光波长为673 nm. 因此, 在本文的计算中, SPCE辐射波长选择为673 nm, 棱镜和银膜在该波长处的折射率分别为1.5145和0.1399 + 4.3157i.

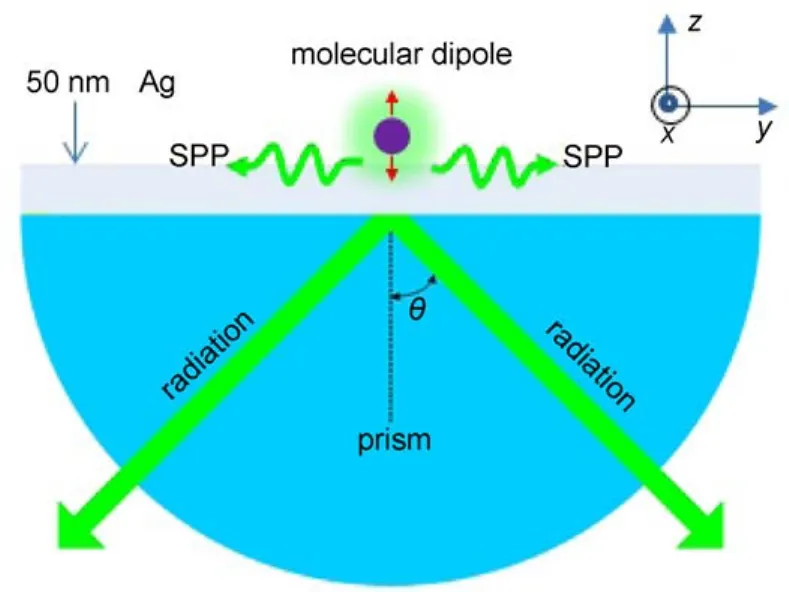
图2 z方向偶极子的SPCE结构示意图Fig.2 Schematic diagram of the SPCE structure with the z-oriented dipole

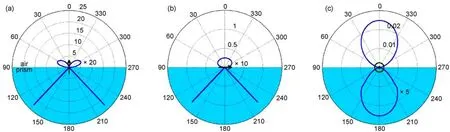
图3 位于银膜表面的电偶极子在不同取向下的辐射功率一维角分布Fig.3 One-dimensional radiation patterns with the molecular dipole of different orientations on the silver layer (a) z-oriented; (b) y-oriented; (c) x-oriented

3.2 SPCE辐射功率密度分布

图3给出了银膜表面不同取向电偶极子的辐射功率密度角分布. 可以看到, 无论电偶极子垂直或者平行于银膜表面, 其辐射功率都可以耦合成SPR模式并定向辐射到棱镜中. 图3(b)和(c)指出, 对于平行于银膜表面的电偶极子, 其辐射功率在平行于电偶极子的平面内有很强的定向辐射, 而在垂直于电偶极子的平面内并没有定向辐射现象. 这是由于电偶极子在与其取向平行的平面内辐射TM偏振波而在与其取向垂直的平面内辐射TE偏振波, 而SPR只能由TM偏振波激发. 定向辐射角度为42.8°,与文献中实验测得的42.9°相差0.1°. 这里定向辐射角被定义为SPCE辐射功率密度最大值对应的角度θ. 图4给出了当电偶极子距离银膜表面一个波长距离(673 nm)时的辐射功率分布. 可以看到, 定向辐射强度大幅度减小而更多的辐射功率进入空气中. 图5给出了定向辐射强度与电偶极子-银膜表面距离之间的关系: 随着距离增大, 定向辐射强度快速减小.这是因为电偶极子辐射功率与SPR模式之间的耦合是近场耦合, 当距离变大时, 其耦合效果自然变差.这一特性说明远离银膜表面的分子的散射信号不能被有效地耦合成SPR模式, 说明了SPCE具有优异的表面选择性.

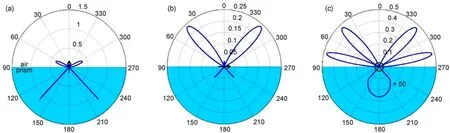
图4 位于银膜上方一个波长处的电偶极子在不同取向下的辐射功率一维角分布Fig.4 One-dimensional radiation patterns with the molecular dipole of different orientations located at a distance of a wavelength over the silver layer

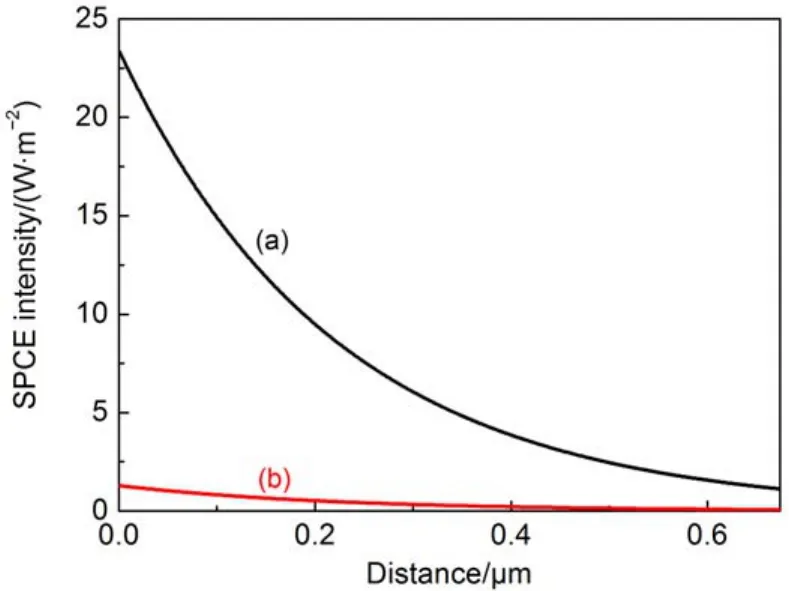
图5 SPCE强度与电偶极子-银膜表面距离之间的关系Fig.5 Dependence of SPCE signal intensity on the distance between the dipole and the silver layer surface

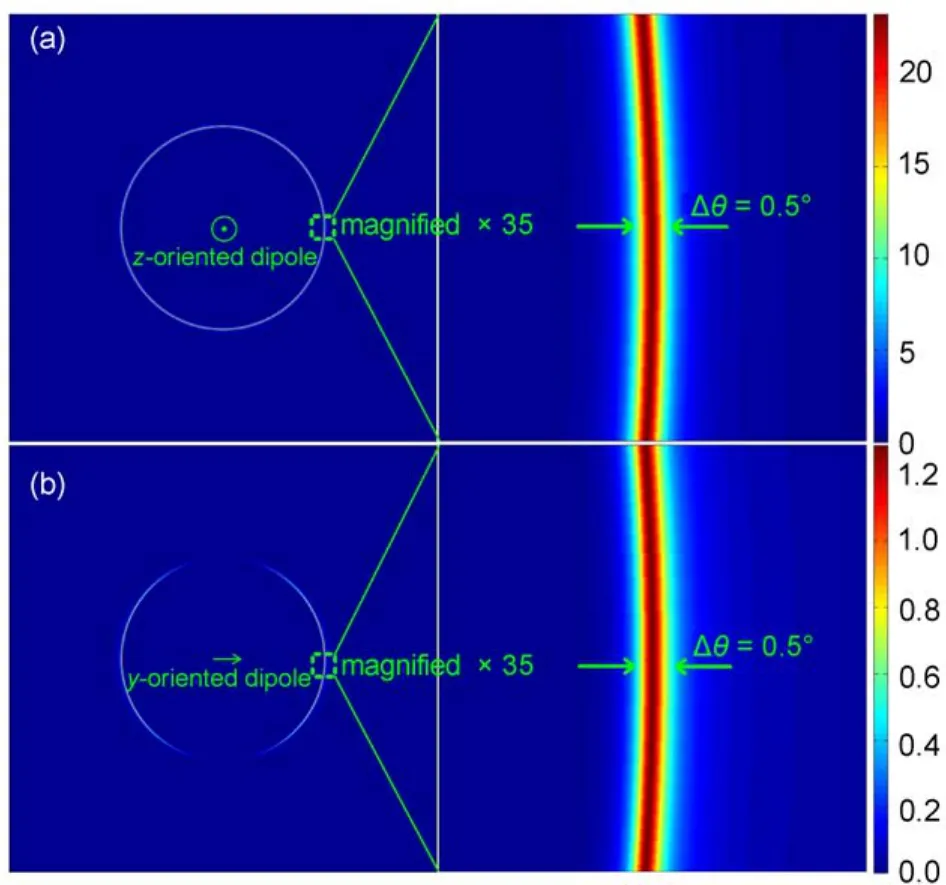
图6 位于银膜表面的电偶极子在不同取向下的辐射功率在棱镜中的二维角分布Fig.6 Two-dimensional radiation patterns with the molecular dipole of different orientations on the silver layer

为了计算辐射到棱镜中的功率占辐射总功率的比例, 我们需要计算电偶极子的二维辐射功率分布. 图6(a)和6(b)分别给出了在银膜表面z取向和y取向的电偶极子在棱镜中的二维辐射功率分布. 可以看到, 辐射功率被很好地限制在定向辐射角度上.对于z取向的电偶极子, 58%的辐射功率被定向辐射到棱镜中. 而对于y取向的电偶极子, 辐射到棱镜中功率比例为31%. 沿z轴取向的电偶极子的定向辐射总功率大于沿y轴取向的电偶极子，这是因为SPR消逝场的z分量大于y分量导致的(即Ez> Ey). 此外，从图6(b)中可以看出沿y轴取向的电偶极子在x-z平面内没有定向辐射，因为SPR消逝场的x分量为0. 图6还指出SPCE信号具有一定的角度发散性，辐射角的半高峰宽(FWHM)为Δθ = 0.5°.

图7 SPCE信号的辐射角对波长的依赖特性Fig.7 Wavelength dependence of the radiation angle of SPCE signal

3.3 SPCE辐射角的波长色散特性

SPCE辐射角和SPR共振角一样具有显著的波长依赖特性, 这一色散特性不利于SPCE信号的高效收集. 图7给出了定向辐射角与波长的关系: 当波长从650 nm增大至810 nm时(对应Δν = 3000 cm–1), 辐射角从42.93°减小至42.40°，变化量为0.53°. 这与文献(14)报道相吻合. 在探测SPCE信号时, 需要综合考虑信号的辐射角随波长的色散关系以及探测器的数值孔径, 从而确定探测器距离反射点的合理距离. 在文献(25)中, 定向探测拉曼散射信号可以同时检测到590和1650 cm–1处的拉曼峰.

3.4 SPCE辐射角FWHM与银膜厚度的关系

SPCE信号的辐射角FWHM不仅依赖于波长,还依赖于银膜厚度. 在实际应用中, SPCE辐射角FWHM不利于信号的高效收集, 尤其在辐射角FWHM较大的情况下, 高效收集更为不易. 图8给出了SPCE辐射角FWHM与银膜厚度的仿真依赖关系.随着银膜厚度从20 nm增大至50 nm, FWHM从3.63°迅速减小至0.50°. 这意味着利用50 nm厚的银膜产生的SPCE信号具有更好的方向性. 另一方面,相同强度的SPCE信号光透过50 nm厚银膜后的衰减度远大于20 nm银膜的情况.17这启示我们: 在优化设计SPCE结构的过程中应该综合考虑金属膜引起的信号衰减和辐射角FWHM两因素.

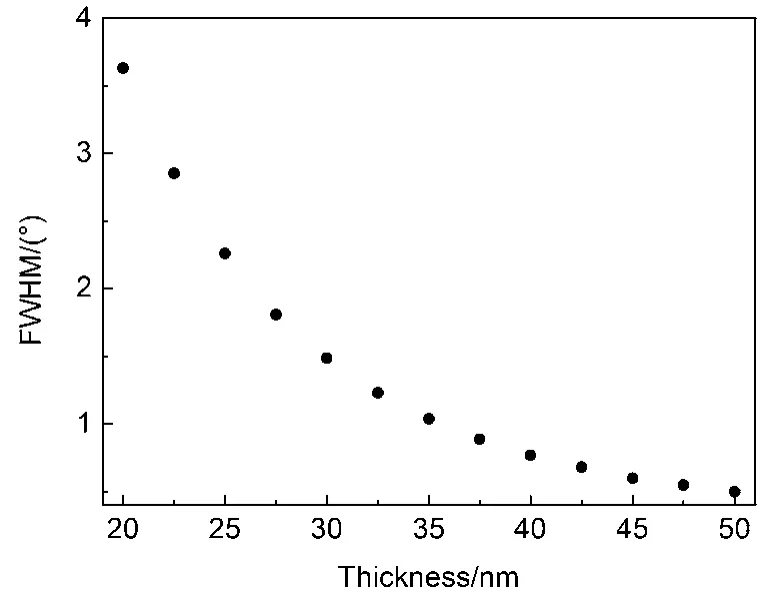
图8 SPCE半高峰宽对银膜厚度的依赖关系Fig.8 Dependence of FWHM of the radiation angle on the thickness of the silver film

4 结 论

本文提出采用光学互易定理计算电偶极子在分层结构中的辐射分布. 通过计算, 我们得到了电偶极子的一维和二维辐射功率密度角分布, 发现SPCE强度与电偶极子的取向以及其与金属薄膜之间的距离有直接关系. 通过二维辐射功率密度角分布, 被定向辐射到棱镜中的功率比例也可以得到:对于垂直于银膜表面的电偶极子, 大约58%的辐射功率进入到棱镜中; 而对于平行于银膜表面的电偶极子, 只有31%的辐射功率进入到棱镜中. 这说明垂直取向的电偶极子比平行取向的电偶极子具有更高的SPR耦合效率. 这一点也与文献报道相一致. SPCE角度具有波长色散特性: 波长越长, 定向辐射角越小.在感兴趣的波数范围内(0–3000 cm–1), 角度变化对接收效果的影响可以通过增大探测器数值孔径和减小探测器与棱镜的距离来规避. SPCE方向性与银膜厚度的关系也通过计算获得: 银膜越薄,辐射功率损耗越小, 但是定向辐射角的半高峰宽越大, 方向性越差. 在SPCE结构的设计中, 要综合考虑损耗和方向性以选取合适的银膜厚度. 本文中计算结果和之前的实验报道吻合很好, 验证了本文提出的计算方法的有效性.

(1)Gao, L. N.; Lu, F. T.; Hu, J.; Fang, Y. Acta Phys. -Chim. Sin. 2007, 23 (2), 274. [高莉宁, 吕凤婷, 胡 静, 房 喻. 物理化学学报, 2007, 23 (2), 274.] doi: 10.3866/PKU.WHXB20070226

(2)Zhu, Z. H.; Zhu, T.; Wang, J.; Liu, Z. F. Acta Phys. -Chim. Sin. 2000, 16 (2), 138. [朱梓华, 朱 涛, 王 健, 刘忠范. 物理化学学报, 2000, 16 (2), 138.] doi: 10.3866/PKU.WHXB20000209

(3)Valdivia, R. H.; Falkow, S. Science 1997, 277 (5334), 2007. doi: 10.1126/science.277.5334.2007

(4)Kneipp, K.; Wang, Y.; Kneipp, H.; Perelman, L. T.; Itzkan, I.;Dasari, R. R.; Feld, M. S. Phys. Rev. Lett. 1997, 78 (9), 1667. doi: 10.1103/PhysRevLett.78.1667

(5)Nie, S. M.; Emery, S. R. Science 1997, 275 (21), 1102. doi: 10.1126/Science.275.5303.1102

(6)Chanda Ranjit, Y.; Haynes, C. L.; Xiaoyu, Z.; Walsh, J. T.; van Duyne, R. P. Anal. Chem. 2004, 76 (1), 78. doi: 10.1021/ ac035134k

(7)Lakowicz, J. R. Anal. Biochem. 2001, 298, 1. doi: 10.1006/abio. 2001.5377

(8)Lakowicz, J. R.; Shen, Y.; D'Auria, S.; Malicka, J.; Fang, J.; Gryczynski, Z.; Gryczynski, I. Anal. Biochem. 2002, 301, 261. doi: 10.1006/abio.2001.5503

(9)Lakowicz, J. R. Anal. Biochem. 2005, 337, 171. doi: 10.1016/j.ab.2004.11.026

(10)Anger, P.; Bharadwaj, P.; Novotny, L. Phys. Rev. Lett. 2006, 96, 113002. doi: 10.1103/PhysRevLett.96.113002

(11)Lee, K. G.; Chen, X. W.; Eghlidi, H.; Kukura, P.; Lettow, R.; Renn, A.; Gotzinger, S.; Sandoghdar, V. Nat. Photonics 2011, 5, 166. doi: 10.1038/nphoton.2010.312

(12)Taminiau, T. H.; Stefani, F. D.; Segerink, F. B.; van Hulst, N. F. Nat. Photonics 2008, 6, 234.

(13)Curto, A. G.; Volpe, G.; Taminiau, T. H.; Kreuzer, M. P.; Quidant, R.; van Hulst, N. F. Science 2010, 329, 930. doi: 10.1126/science.1191922

(14)Lakowicz, J. R. Anal. Biochem. 2004, 324, 153. doi: 10.1016/j.ab.2003.09.039

(15)Chen, C.; Li, J. Y.; Wang, L.; Lu, D. F.; Qi, Z. M. Phys. Chem. Chem. Phys. 2015, 17, 21278. doi: 10.1039/C4CP05092D

(16)Li, H.; Xu, S.; Liu, Y.; Gu, Y.; Xu, W. Thin Solid Films 2012, 520 (18), 6001. doi: 10.1016/j.tsf.2012.04.084

(17)Nils, C. Anal. Chem. 2004, 76, 2168. doi: 10.1021/ac049925d

(18)Zhao, Q.; Lu, D. F.; Liu, D. L.; Chen, C.; Hu, D. B.; Qi, Z. M. Acta Phys. -Chim. Sin. 2014, 30 (7), 1201. [赵 乔, 逯丹凤, 刘德龙, 陈 晨, 胡德波, 祁志美. 物理化学学报, 2014, 30 (7), 1201.] doi: 10.3866/PKU.WHXB201405191

(19)Hu, D. B.; Chen, C.; Qi, Z. M. J. Phys. Chem. C 2014, 118 (24), 13099. doi: 10.1021/jp502171k

(20)Hu, D. B.; Qi, Z. M. J. Phys. Chem. C 2013, 117 (31), 16175. doi: 10.1021/jp4052903

(21)Van Orden, A.; Machara, N. P.; Goodwin, P. M.; Keller, R. A. Anal. Chem. 1998, 70 (7), 1444. doi: 10.1021/ac970545k

(22)Carminati, R.; Nieto, M. J. Opt. Soc. Am. 1998, 15, 706. doi: 10.1364/JOSAA.15.000706

(23)Ru, E. C. L.; Etchegoin, P. G. Chem. Phys. Lett. 2006, 423 (1), 63.

(24)Hu, D. B. Resonant Mirror Enhanced Surface Raman Spectroscopy. Ph. D. Dissertation, University of Chinese Academy of Sciences, Beijing, 2014. [胡德波. 共振镜增强的表面拉曼光谱技术[D]. 北京: 中国科学院大学, 2014.]

(25)Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge University Press: Cambridge, 1999; pp 38–70.

(26)Meyer, S. A.; Le Ru, E. C.; Etchegoin, P. G. Anal. Chem. 2011, 83, 2337. doi: 10.1021/ac103273r

Simulation of Surface Plasmon Coupled Emission with Silver Film

CHEN Chen1LU Dan-Feng1CHENG Jin1QI Zhi-Mei1,2,*
(1State Key Laboratory of Transducer Technology, Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, P. R. China;2State Key Laboratory of NBC Protection for Civilian, Beijing 102205, P. R. China)

Surface plasmon coupled emission (SPCE) is a physical process opposite to conventional surface plasmon resonance (SPR) with Kretschmann configuration: if a molecule is close enough to the metal surface, the photons generated by excitation of the molecule will be coupled to the SPR mode that is then transformed into the far-field beam propagating at the resonance angle. SPCE serving as a powerful surface-selective analytical technique has been recently used in fluorescence and Raman spectroscopies, and it has several advantages such as repeatable field enhancement, high collection efficiency, and great surface selectivity. In this work, we simplified the simulation of SPCE based on the optical reciprocity theorem. We obtained the radiation patterns of the excited molecule with different orientations, the surface selectivity of SPCE, the wavelength dependence of the radiation angle, and the relationship between the full-width at half-maximum (FWHM) of the radiation angle and the thickness of a silver layer. These simulated results fit almost perfectly with the experimental results reported previously.

Surface plasmon coupled emission; Optical reciprocity theorem; Surface plasmon resonance; Fluorescence spectroscopy; Raman spectroscopy

O644

10.3866/PKU.WHXB201509182

Received: May 25, 2015; Revised: September 6, 2015; Published on Web: September 18, 2015.

*Corresponding author. Email: zhimei-qi@mail.ie.ac.cn; Tel: +86-10-58887196.

The project was supported by the National Key Basic Research Program of China (973) (2015CB352100), National Natural Science Foundation of China (61377064, 61401432) and State Key Laboratory of NBC Protection for Civilian, China (SKLNBC2014-11).

国家重点基础研究发展规划项目(973) (2015CB352100), 国家自然科学基金(61377064, 61401432)和国民核生化灾害防护国家重点实验室开放基金项目(SKLNBC2014-11)资助

©Editorial office of Acta Physico-Chimica Sinica