双平台鱼雷报警声呐对来袭鱼雷快速定位仿真

王奔波，吴 磊

(1.南海舰队装备部，广东 湛江524001;2.中国人民解放军91388 部队，广东 湛江524022)

0 引 言

鱼雷是水面舰艇的主要威胁之一。随着鱼雷武器的发展，水面舰艇面临的鱼雷威胁越来越严重［1］。为了达成有效的水下防御，舰艇应该有足够的时间来实施对抗和机动规避，因而需要对远距离来袭鱼雷进行早期报警［2］。要获取鱼雷信息必须依赖于鱼雷报警声呐，研制专用的水面舰鱼雷报警声呐也是各国海军主要的发展方向，如法国的Albatros鱼雷报警声呐、俄罗斯的Vignette-em型鱼雷报警声呐［3］。鱼雷报警应具有3个要素，即鱼雷来袭方位、鱼雷识别和鱼雷至被攻击舰艇的距离。在鱼雷报警距离较远的情况下，为了及时实施水声对抗的准备工作，首先应该知道来袭鱼雷的精确方位，将表征鱼雷的多种信息相融合，迅速准确的对鱼雷实施报警，对鱼雷定位是对鱼雷实施水声对抗的关键，而且是对鱼雷报警跟踪的最后环节［4］。对于来袭鱼雷进行定位距离越远，则水面舰实施水声对抗的成功率越大。使用适于鱼雷目标检测识别的被动拖线阵虽然可以解决远距离鱼雷报警问题，却只能提供来袭鱼雷的方位信息。有效防御鱼雷攻击迫切需要鱼雷目标的距离信息［5］。

本文针对水面舰进行编队反潜作战，利用被动工作方式的鱼雷报警声呐能够对较远距离来袭的鱼雷进行精确测向的优势，在2个水面舰平台(以下简称双平台)鱼雷报警声呐同时探测到来袭鱼雷的情况下，对鱼雷快速定位方法进行仿真分析，对舰艇编队作战时防御鱼雷攻击的方法研究具有一定的借鉴意义。

1 双平台鱼雷报警声呐对来袭鱼雷快速定位原理

编队反潜作战时，2艘水面舰的鱼雷报警声呐对来袭鱼雷探测示意图如图1所示，水面舰编队由W1和W2组成，其航速分别为V1和V2，航向分别为H1和H2;来袭鱼雷为M1，鱼雷航速航向分别为V3和H3，鱼雷M1在某一时刻与水面舰W1和W2的距离分别为D1和D2，水面舰W1和W2探测到鱼雷的舷角分别为α1和α2，舷角设定左舷为正、右舷为负。一般情况下V1=V2，H1=H2。

由于鱼雷报警声呐多为拖曳线列阵声呐，其位置中心与水面舰GPS 天线位置不同，在实际计算过程中需要进行修正，为了描述方便，下面提到的水面舰W1和W2坐标位置为鱼雷报警声呐位置中心。

如图2所示，建立以W1的实时位置为原点、航向H1为x 轴正方向的直角坐标系，W1坐标为(x1，y1)= (0，0)，W2坐标为(x2，y2)，M1坐标为(x3，y3)。依据图2 中几何关系可知:

W1和M3的连线表达式为:

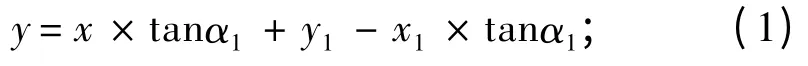
W2和M3的连线表达式为:

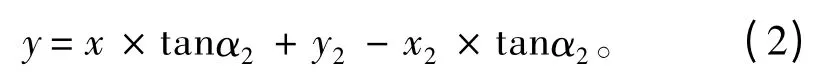
式(1)与式(2)联立求得:

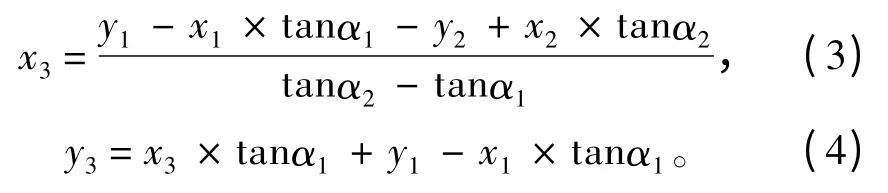
式中:W1(x1，y1)和W2(x2，y2)由2个水面舰GPS 实时定位值和GPS 天线安装位置与鱼雷报警声呐中心位置修正转换得出［5］;α1和α2由2个水面舰的鱼雷报警声呐给出。在上面的处理过程中忽略了鱼雷辐射噪声到达2艘水面舰时的时间延迟差值，这是因为声速远远大于鱼雷的航速，因此当精度要求不是很高时，为了简化计算，可以忽略它对定位精度的影响。

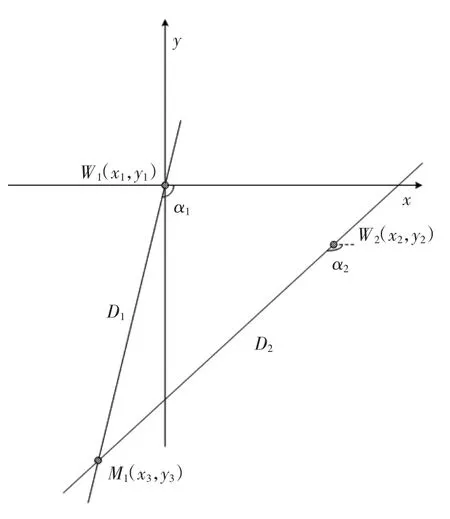
图2 鱼雷位置坐标求解Fig.2 The solution for coordinates of torpedo

通过上述过程可知，采取该方法进行远距离鱼雷快速定位时，主要误差来源是水面舰GPS 定位误差、鱼雷报警声呐的舷角测量误差以及时延带来的误差。通过仿真计算，分析各误差源对定位精度的影响，找出主要的误差来源，研究采取该方法进行鱼雷快速定位的可行性。

2 仿真分析

当2个水面舰平台同时探测到来袭鱼雷时，通过上一节阐述的方法，可以很容易的得出鱼雷的实时位置，下面采用仿真计算的方式分析各误差因素对鱼雷的定位精度的影响。

在仿真过程中，加入的随机误差为相互独立、零均值、均方根值相等的随机数组，其长度为1 000，经过1 000 次循环计算后，得到的1 000 组计算鱼雷估计坐标与鱼雷真值坐标相减，然后求解均方根即为所求误差。

2.1 水面舰GPS 定位误差对定位精度的影响

GPS 定位误差直接影响水面舰坐标准确度。

仿真过程中，坐标距离单位为m，水面舰W1真值坐标为(x1，y1)= (0，0)，W2真值坐标为(x2，y2)=(1 500，500)，鱼雷真值坐标(x3，y3)，仿真步骤如图3所示。

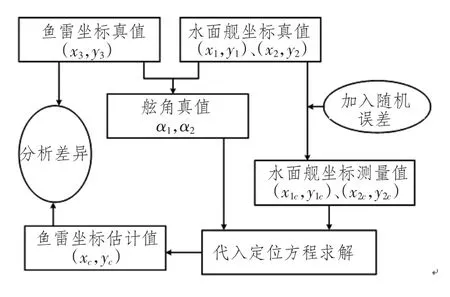
图3 仿真流程图1Fig.3 The simulation flow chart 1

图4(a)为GPS 存在误差时，定位误差随着GPS误差变化的曲线，此时(x3，y3)=(－1 500，－5 500);图4(b)为GPS 误差均方根值为2 m 时，定位误差随着x3变化的曲线，此时y3=－5 500;图4(c)和(d)为GPS 误差均方根值为2 m 时，定位误差随着y3变化的曲线，此时x3分别为－1 500，3 000。

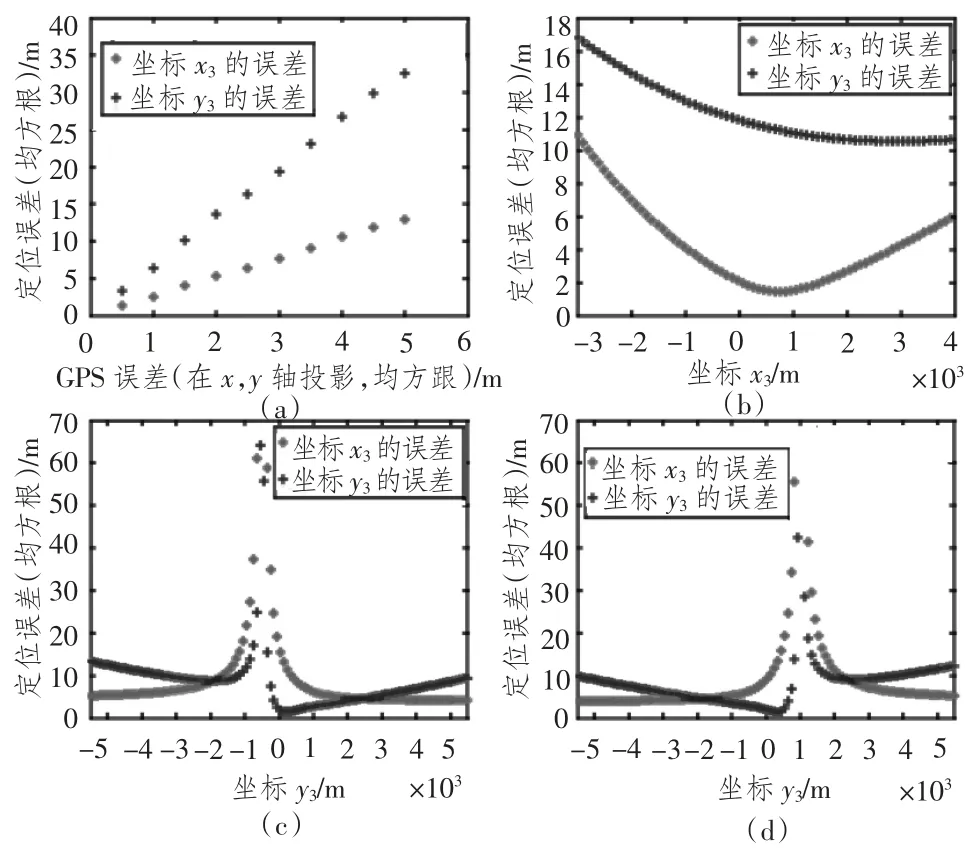
图4 定位误差随着GPS 误差，x3，y3的变化曲线Fig.4 Variation curves of position error versus GPS error，x3，y3

仿真结果表明:随着GPS 误差的增大，鱼雷的定位误差增大;鱼雷相对于2艘水面舰位置不同时，误差也会有所不同，当鱼雷位置向两舰连线垂线的方向靠近时，误差会减小，而当鱼雷位置接近两舰连线方向时，误差会显著增大。

2.2 鱼雷报警声呐舷角测量误差对定位精度的影响

仿真条件同上，假定舷角测量误差范围为0.1°～1°。仿真步骤如图5所示。

图6 (a)为鱼雷报警声呐存在舷角测量误差时，定位误差随着舷角测量误差变化的曲线，此时(x3，y3)=(－1 500，－5 500);图6 (b)为舷角测量误差误差均方根值为0.3°时，定位误差随着x3变化的曲线，此时y3=－5 500;图6 (c)和图6 (d)为舷角测量误差误差均方根值为0.3°时，定位误差随着y3变化的曲线，此时x3分别为－1 500和3 000。

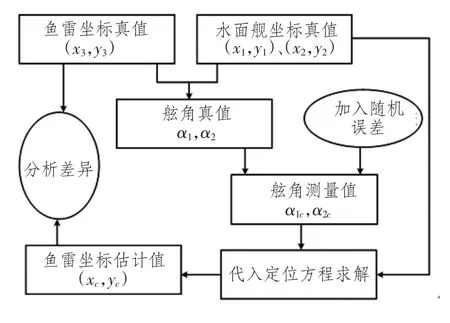
图5 仿真流程图2Fig.5 The simulation flow chart 2

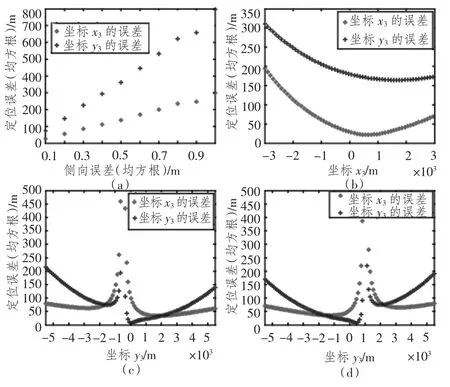
图6 定位误差随着舷角测量误差，x3，y3的变化曲线Fig.6 Variation curves of position error versus relative bearing error，x3，y3

仿真结果表明:鱼雷报警声呐的舷角测量误差对鱼雷定位误差的影响规律与GPS 误差类似，不过鱼雷报警声呐测向误差对鱼雷定位精度影响更大，随着测向误差的变大，鱼雷定位精度明显降低。

2.3 时延对定位精度的影响

时延包括鱼雷辐射噪声到水面舰的传播时间和双平台协同定位计算消耗的时间。鱼雷是水下高速运动的目标，时延越长，定位误差必然越大。下面对时延带来的定位误差进行仿真分析，仿真过程中忽略时延差的影响，选择鱼雷攻击弹道为目标舰的现在方位［7］。

仿真过程中，水面舰航速为20 kn，鱼雷航速为40 kn，水面舰航向为90°，鱼雷航向为鱼雷与水面舰W2连线方向，声速为c=1 500 m/s，其他条件同上。假定A 时刻为鱼雷辐射噪声的时刻，B 时刻为水面舰接收到鱼雷辐射噪声的时刻，C 时刻为双平台协同计算得出鱼雷位置的时刻，在C 时刻计算得出的鱼雷坐标是鱼雷在A 时刻的坐标位置，时延差为tC－tA。仿真步骤如图7所示。

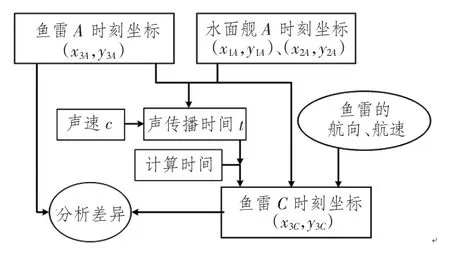
图7 仿真流程图3Fig.7 The simulation flow chart 3

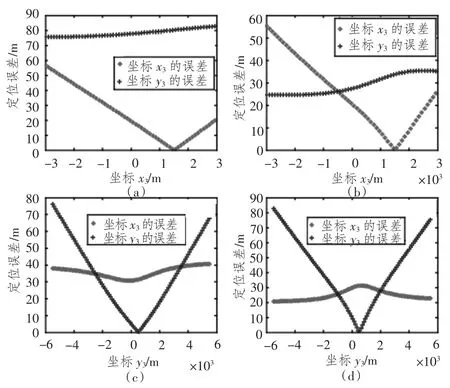
图8 定位误差随着x3，y3的变化曲线Fig.8 Variation curves of position error versus x3，y3

图8(a)和图8(b)为时延带来的定位误差随着x3变化的曲线，此时y3分别为－5 500、2 500;图8(c)和图8(d)为时延带来的定位误差随着x3变化的曲线，此时x3分别为－1 500，3 000。

仿真结果表明:鱼雷与水面舰之间的距离越远，时延带来的误差越大;时延带来的误差与鱼雷和水面舰(目标)的连线方向密切相关。当然，时延带来的误差可以通过连续多次定位计算后进行预估和修正。

3 结 语

在水声对抗过程中，当双平台都能够对来袭鱼雷进行报警时，采用该方法可以快速的对远距离鱼雷进行定位。本文对鱼雷定位的误差进行了仿真分析，仿真结果表明，由于舰载GPS 定位精度一般较高，由GPS 定位误差对鱼雷定位精度影响不大;时延误差与距离和方位有关;鱼雷报警声呐对鱼雷的舷角测量误差是鱼雷定位误差的主要来源;当舷角测量误差较小时，采取该方法能够快速获取较精确鱼雷位置，可为远距离实施水声对抗提供参考。在后续的研究工作中，将继续对舷角测量误差对鱼雷定位的影响进行分析，以求进一步提高该方法的定位精度。

［1］张宝华.国外舰用鱼雷报警声呐发展综述［J］.声学与电子工程，2013，110(2):47－49.

［2］阎福旺.水声对抗技术［M］.北京:海洋出版社，2003.

［3］杨日杰，高学强，韩建辉.现代水声对抗技术及应用［M］.北京:国防工业出版社，2008.

［4］李伟，汪洪升，田德海.基于舰艇水下先期防御的来袭鱼雷报警系统［J］.鱼雷技术，2011，19(1):260－262.

［5］陈敬军.水面舰艇鱼雷防御系统中鱼雷报警纵览［J］.声学技术，2013，32(3):257－262.

［6］杜娟，朱华邦.基于GPS 技术的舰载探测系统标校方法研究［J］.火控雷达技术，2013，42(1):17－20.

［7］孟庆玉，张静远，宋保维.鱼雷作战效能分析［M］.北京:国防工业出版社，2003.