基于混沌神经网的海上无线通信资源算法设计

赵 杨，高江华

(1.江门职业技术学院，广东 江门529090;2.日照职业技术学院，山东日照276800)

0 引 言

现代海上运输及军事领域，基于无线通信的应用越来越多，如海上视频监测系统﹑海上气象传感网络系统﹑军事调度系统及数据融合系统等，需要进行大量的数据传输，所占带宽较大，而海上无线资源有限，需要对这些资源进行合理分配才能保障这些业务的有效运行。

海上无线通信资源分配［1］及优化具体说是对整个海上无线通信系统之间的空中接口资源，如通信带宽﹑信号频谱以及传输时隙的管理，包括信道复用﹑分组调度﹑网络优化﹑负载均衡等相关方法，通过最大限度的合理利用无线网络资源来提升整个通信系统的效率。在现有的海上无线通信资源优化算法中，有基于自适应反馈﹑无线协作信道复用技术等，现有的无线资源算法普遍存在复杂度较高，并且最终计算结果与最优解之间还有一定的空间。

本文研究了现有的海上无线资源优化算法，对现有的混沌神经网络进行优化改进，有效的降低了整个算法的复杂度，并使参数的设置更符合海上无线通信环境，同时通过大量测试提供了混沌神经网络的参数集，提出了基于混沌神经网络海上无线资源优化算法，并给出仿真结果。

1 混沌神经网络原理

1.1 混沌神经网络模型

混沌神经网络［2－3］能够精确的找出通信网络中的平衡点及周期规律，是现代信息处理技术中最热门的技术之一，具有良好的动力学特性。其缺点是算法容易陷入局部最优的陷阱，并且算法的收敛性不高，需要进行局部优化。

混沌神经网络如图1所示，是一个自反馈递归系统，每次的计算结果作为下一次迭代过程的初始条件重新进行计算，整个网络成收敛性，系统达到稳态时，迭代过程结束。

1.2 混沌神经网络数学描述

如图1所示，网络有N个处理单元，每个处理单元含有一个权值放大器。如处理单元i，通过权值叠加器Ii与电阻Rij、电容Ci组成电路，输出电压为ui作为放大器的前端输入，经过运算放大器后的输出结果为vi。

而图1 中的wij为处理单元j与i 之间的反馈权值系数。若:

根据基尔霍夫公式得到:

混沌神经网络系统能量定义如下:

式中f-1为混沌神经系统激励函数的逆变换。对式(3)中的混沌神经网络系统能量进行求导，得到:

通常混沌神经系统激励函数呈现单调递增性，所以:

对以上公式进行分析，整个混沌神经系统的能量函数呈现单调递减特性，并且值为非正。当整个系统的输出趋于稳定时，混沌神经网络系统能量处于一个极小值，此时整个网络处于全局或局部最优。

2 基于混沌神经网的OFDAM优化

2.1 无线OFDAM 资源优化模型

现有海上无线通信系统主要基于多用户OFDAM技术［4］，其资源分配主要有动态资源分配及静态资源分配2 种模式，现有多是基于动态分配，其原理如图2所示。

图2 OFDMA 系统无线资源分配原理图Fig.2 The diagram of radio resource allocation based on OFDMA system

假设RT为海上无线通信系统的信号传输率;RT为系统发射功率;PE为多信道误码率总和;BER为单一通道的误码率。海上无线通信对于信号比特、功率及载波负载的优化数学模型如下:

最终的优化目标:

并且需要满足:

上述的对于海上无线资源的优化问题通过式(8)～式(12)限制的条件形成不同的寻找平衡点模型，其中式(7)表示对无线通信网络发射功率的最优公式，式(6)表示对各业务系统的最大带宽的最优求解。

限制条件式(8)表示子信道i 分配的具体业务范围，通过条件(9)限制一个子信道只能由一个具体的业务使用，式(10)表示各子信道的发射功率为正，式(11)限定了各业务的总功率之和不能超过最大的额定功率，式(12)则代表了各个不同业务对信号传输速率的要求。

2.2 基于混沌神经网络的优化算法

混沌神经网络利用相位空间［5］，在全局范围内进行快速搜索。相比较之前的算法，解决了陷入局部最优的缺点，并且收敛性较之前有很大的提高。

基于神经网络的海上无线资源优化模型如下:

式中:Ux，j(t)为信息处理元的瞬时状态;Vx，j(t)为在时刻t的网元输出;u0为信息处理单元的权重因子系数;λ为收敛阻尼系数;a为正相关比例因子;wx，i:y，j(t)为2个信息处理单元之间的相关连接系数;zx，i(t)为递推负反馈因子;I0为正的常数;β为反馈衰减因子。

在海上多业务的OFDMA 无线通信系统中，信号调制方法采用M－QAM，则用户所在业务x 在子信道i 上的每帧含有cx，i个比特，MT=2cx，i。若子信道i的增益系数为，则传输cx，i个比特所需发射功率的最优值为:

式中:

式中Pe为系统控制的误码率。

最终每个业务所占信道的最优发射功率由N0，Pe，及调制方式确定。

在具体的海上无线通信应用场景中，业务可以根据所需要的带宽占用多个传输子信道，当使用的信道数为N 时，单位时间内业务x 所传输的总的比特数有如下表达式:

由无线通信中的功率最小准则，当海上无线通信系统的总误码率及传输速率及带宽确定后，整个无线系统的发射功率达到最优，功率公式如下:

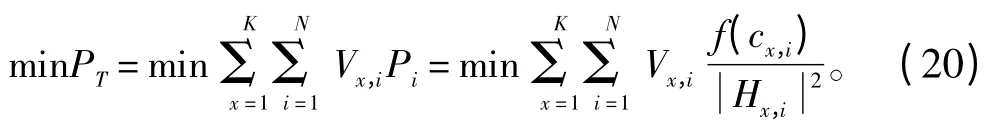
3 算法仿真

本文在Matlab 平台对基于混沌神经网络的海上OFDMA 单小区无线通信系统资源优化算法进行仿真，基站置于网络中心位置，载波频率设为2 GHz。海上通信业务数为4。用户数为6，综合优先等级为1∶2∶2∶3∶4∶4，，算法的详细参数设置如表1所示。

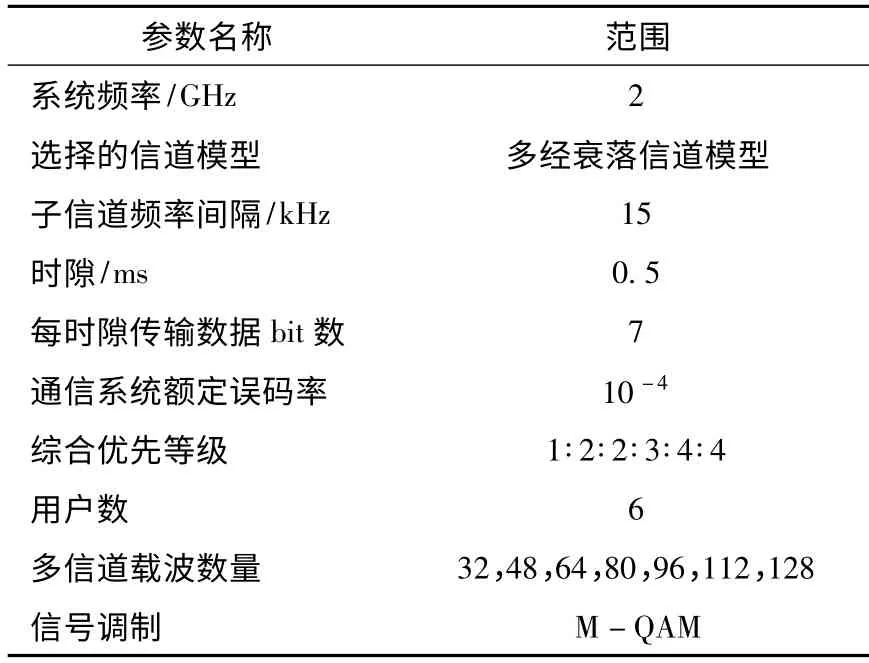
表1 参数设置表Tab.1 Parameter setting

本文仿真的混沌神经网络结构为二维模型，信号处理单元格数分布为K × N，其中K为用户数，N为业务数。整个海上无线通信信道增益矩阵为H，具体参数Hx，i为业务在多经信道中的增益系数。整个混沌网络参数如下:u0= 7，a= 0.06，λ= 0.95，I0=0.65，z(0)=0.89，Ae=0.15，Be=2.5，Ce=6，De=2，Fe=3。

最后给出本文算法和ESA 资源优化算法误码率曲线如图3所示。

图3 误码率曲线图Fig.3 The curve of bit error rate

4 结 语

在海上无线通信领域，随着业务及用户的增加，其无线资源呈现越来越紧张的趋势。如何高效的对资源进行分配及合理利用是保障各项业务运行的关键。在现有的海上无线通信资源优化算法中，有基于自适应反馈﹑无线协作信道复用技术等，其普遍存在算法复杂度较高，并且最终的计算结果与最优解之间还有一定的空间。

本文研究了现有的海上无线资源优化算法，提出了基于利用混沌神经网络海上无线资源优化算法，并给出仿真结果。

［1］KIRKPATRICK S，GELATT C D，VECCHI M P.Optimization by simmulated annealing［J］.Science，New Series，1983，220(4598):671－680.

［2］LOU X，YE Q，CUI B.Stabilization analysis of stochastic Hopfield neural networks［C］//Control，Automation and Systems (ICCAS)，2012 12th International Conference on.IEEE，2012:930－933.

［3］GUMI J P，WEIDLIEH R B.A derivative of the hopfieldtank neural network model that reliably solves the traveling salesman problem［C］//International Joint Conference on Neural Networks，1989:11－588.

［4］刘刚，钟小军，董鹏.基于遗传算法和神经网络的舰船电子装备备件优化模型研究［J］.舰船科学技术，2008，30(10):138－141.LIU Gang，ZHONG Xiao-jun，DONG Peng.Research on warship electronic equipm ents spare parts optmi izemodelbased on genetic algorithm and neural network［J］.Ship Science and Technology，2008，30(10):138－141.

［5］张瑜，贺秋瑞.基于混合系统的微弱信号参数提取方法［J］.舰船科学技术，2013，35(12):13－16.ZHANG Yu，HE Qiu-rui.The method of weak signal parameters extraction based on hybrid system［J］.Ship Science and Technology，2013，35(12):13－16.