离散量子粒子群优化的认知无线电频谱分配
刁 鸣,张志强,高洪元
(哈尔滨工程大学信息与通信工程学院,哈尔滨150001)
·移动互联与通信技术·
离散量子粒子群优化的认知无线电频谱分配
刁 鸣,张志强,高洪元
(哈尔滨工程大学信息与通信工程学院,哈尔滨150001)
为解决认知无线电频谱分配的离散优化问题并提高分配性能,提出一种离散量子粒子群优化算法。利用量子计算理论更新粒子并用波函数对量子旋转角进行调节,使之同时具有粒子群优化算法快速收敛和量子计算精度高的优点,从而有效提高认知无线电频谱分配的性能。仿真结果表明,与遗传算法、量子遗传算法、粒子群优化算法和敏感图论着色算法相比,该算法能较快地搜寻到最优解,且在不同的网络效益函数下性能较优。
认知无线电;频谱分配;离散优化;离散量子粒子群优化算法;网络效益函数
1 概述
目前,频谱资源变的越来越匮乏,而对有限的频谱资源的利用率较低又成为一个更为严重的问题[1-2]。为了解决这一问题,认知无线电(Cognitive Radio,CR)技术应运而生,它作为一种智能无线通信系统,能感知无线环境的变化并通过实时地修改操作参数对其做出反应,从而为提高无线网络的频谱利用率提供了一种有效的方法[3-4]。这样的无线网络中,在特定的时间和位置上,主用户未使用的频谱由次级用户(或认知用户)识别和接入。为了不影响主用户的工作,次级用户接入时要满足与干扰和冲突有关的约束条件。在认知无线电领域中,频谱分配问题是一个研究的热点,最大化频谱利用率的同时维护系统的公平性是其主要目标[2,5-6]。
在主用户和次用户中分配信道同时最小化所有用户之间干扰的问题在认知无线电网络中被称为资源分配或者频谱分配问题。文献[7]把这个问题称为NP难问题。如今,已有很多分配模型用来解决认知无线电频谱分配问题,如图论着色模型[8-9]、干扰温度模型[10]、定价拍卖模型和博弈论模型[11]。近年来,进化算法被用来解决这个问题,如遗传算法[10,12]、粒子群优化算法[10,13]、人工蜂群算法[11]、量子遗传算法[14]。但是这些经典的进化算法都存在收敛速度和收敛性能之间的矛盾,在现有条件下很难在保证收敛速度的条件下避免局部收敛,准确搜索到最优解。因此,需要根据进化算法的发展提出新算法来解决现有问题。
量子粒子群优化算法是基于传统粒子群算法的改进。目前,量子粒子群优化算法在函数优化、系统辨识、生物信息、图像处理和工程优化等许多方面得到广泛应用,并取得了较好的应用效果。传统量子粒子群优化算法将量子行为引入粒子群算法,提高了收敛精度,但不适用于实际离散空间的搜索,因而不能有效解决认知无线电频谱分配的问题。为此,本文对粒子群算法量子化,利用量子计算理论更新粒子,并用波函数对量子旋转角进行调节,提出一种离散量子粒子群优化算法(Discrete Quantum-behaved Particle Swarm Optim ization,DQPSO)。
2 CR频谱分配模型
认知无线电频谱分配模型由可用频谱矩阵、效益矩阵、干扰矩阵、无干扰分配矩阵构成。假设在一个认知无线电网络中有N个认知用户(标号为1~N)、M个可用频带(标号为1~M),且各频带之间相互正交[3]。模型中各矩阵定义如下:
(1)可用频谱矩阵L:L={ln,m|ln,m∈{0,1}}N×M是一个N行M列的矩阵,ln,m表示频带m对用户n的可用性。如果频带m可以被认知用户n使用,则ln,m=1;如果频带m不能被认知用户n使用,则ln,m=0。
(2)效益矩阵B:B={bn,m}N×M是一个N行M列的矩阵,bn,m表示用户n使用频带m时所获得的效益。效益可以用频谱利用率、吞吐量来表示,本文中,效益正比于认知用户通信覆盖面积。如果ln,m= 0,则bn,m=0。
(3)干扰矩阵C:C={cn,k,m|cn,k,m∈{0,1}}N×N×M是一个N×N×M的三维矩阵,cn,k,m表示用户n和用户k同时使用频带m时的干扰约束关系。如果cn,k,m=1,则认知用户n和k同时使用频带m时会产生干扰。干扰矩阵和可用频谱矩阵之间也有制约关系,当n=k时,cn,n,m=1-ln,m。
(4)无干扰分配矩阵A:A={an,m|an,m∈{0,1}}N×M是一个N行M列的矩阵,表示一种可行的频谱分配方案。如果将频带m分配给认知用户n,则an,m=1;如果频带m没有分配给认知用户n,则an,m=0。无干扰分配矩阵A必须满足如下无干扰约束条件:
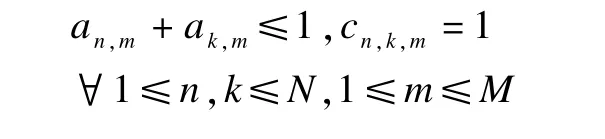
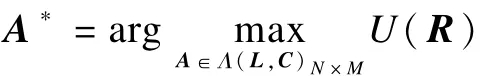
(1)平均最大网络效益:
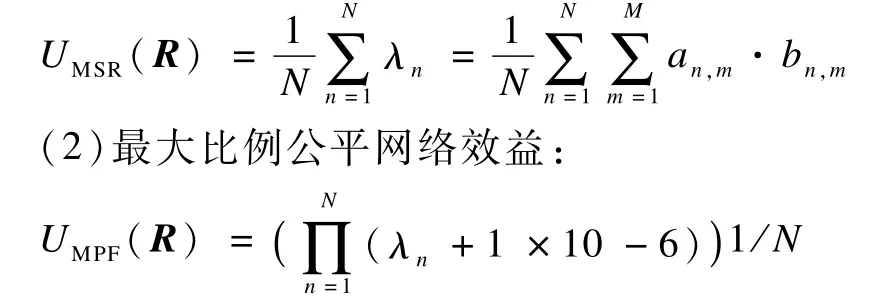
3 离散量子粒子群优化算法

其中,满足|αij|2+|βij|2=1(i=1,2,…,h;j=1,2,…,l),则量子速度可以表示为2l个状态。为了简单有效地设计DQPSO算法,设定αij和βij为实数,并
传统量子粒子群优化算法难以解决认知无线电频谱分配的离散搜索问题,为此,本文在粒子群优化算法中引入量子计算理论来更新粒子,并用波函数对量子旋转角进行调节,提出DQPSO算法。
在DQPSO算法中使用量子编码,称之为量子比特或者Q比特,基于量子比特的概念,量子速度的概率表示定义为一个量子比特串。DQPSO中每一位采用量子比特的方式表示,称为量子位,由一对复数(α,β)表示。每个量子位的状态可以取0或1,|α|2,|β|2分别表示量子位处于0或1的概率,设共有h个量子粒子,那么第i个量子粒子的量子速度定义为:
且0≤αij≤1,0≤βij≤1。因此,,式(1)中的量子速度可以简化为:
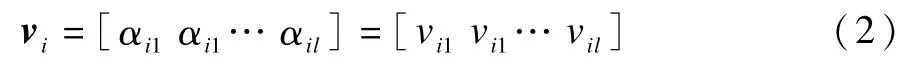
在离散量子粒子群优化算法中,每个量子粒子依靠其自身和周围量子粒子的历史经验于l维空间中运动。在这个l维空间中共有h个量子粒子,第i个量子粒子在空间中的位置表示为向量xi=[xi1,xi2,…,xil](i=1,2,…,h),第i个粒子的量子速度表示为向量vi=[vi1,vi2,…,vil](i=1,2,…,h),第i个量子粒子的个体最优位置表示为向量pi=[pi1,pi2,…,pil](i=1,2,…,h),向量pg=[pg1,pg2,…,pgl]代表至今为止群体中所有量子粒子探索到的最优位置。
通过以上分析,将量子粒子的更新过程表示如下:
量子速度的进化过程主要依靠量子旋转门[15]来进行,量子旋转角的更新方法为:

其中,i=1,2,…,h;j=1,2,…,l;s为[1,h]之间的随机整数;e1,e2为加速因子;φ表示调整系数;u是[0,1]之间均匀分布的随机数;t和t+1代表迭代次数。
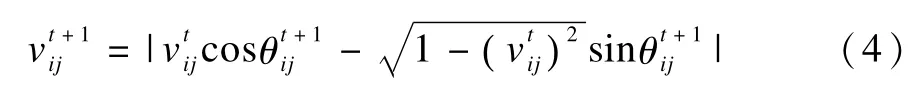
这样,第i个量子粒子的第j个量子位速度vij由如下式方法进行更新:其中,i=1,2,…,h;j=1,2,…,l;t和t+1代表迭代次数。
最终,每一代的第i个量子粒子的量子位置通过如下方程更新:

4 离散量子粒子群优化的CR频谱分配算法
量子粒子群的初始位置在位置空间中随机选择,所有粒子的量子速度初始化为。目标函数的目的是评价每一个量子粒子的状态,在频谱分配问题中,位置优化的目标是最大化网络效益。
基于以上分析,离散量子粒子群优化算法用于频谱分配的工作流程表示如下:
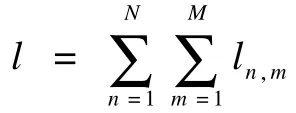
步骤2 基于二进制编码和量子编码机制产生一个初始的量子粒子种群。
步骤3 对每个量子粒子位置的第j个量子位映射到an,m中,其中,(m,n)为L1中的第j个元素,且j=1,2,…,l。对所有的m,搜寻所有满足cn,k,m=1且n≠k的(n,k),检查矩阵A的第n行、m列与矩阵A的第k行、m列两位对应的元素是否同时为1,如果是,随机置其中一位为0。
步骤4 计算每个量子粒子的适应度值。
步骤5 更新每个量子粒子的个体最优位置,更新量子粒子群体的全局最优位置。
步骤6 更新每个量子粒子的量子速度和量子位置。
步骤7 如果算法达到预定义的最大进化代数,则停止并输出最优结果;如果没有,则转到步骤3。
5 性能仿真及结果分析
敏感图论着色算法是为了描述认知无线电频谱分配模型而提出的解决认知无线电频谱分配问题的常用算法。为检验DQPSO频谱分配算法的性能,在仿真中将其与CSGC算法以及其他进化算法进行比较。CSGC算法使用非协作式标签规则。
本文将4种进化算法设置成相同的初始种群和最大进化代数(最大进化代数设置为1 000)。GA,QGA,PSO的参数设置与DQPSO相同[16]。在DQPSO算法中,设定e1=0.06,φ=0.1。每一次实验仿真100次。
5.1 基于平均最大网络效益的仿真实验
设置主用户数为20,可用信道数为20,次级用户数为10。仿真结果如图1所示。其中,纵坐标代表算法使用平均最大网络效益函数时获得的效益。可以看出,CSGC算法效果最差,GA,QGA,PSO算法容易陷入局部最优,DQPSO算法虽然在收敛速度上较PSO算法有一定差距,但是在150代以后DQPSO算法获得的平均最大网络效益明显高于其他算法。

图1 基于平均最大网络效益的收敛曲线
保持次级用户数为10不变,逐渐增加信道数c,并使主用户数与信道数相等,通过仿真研究平均最大网络效益的变化,得到结果如表1所示。可以看出,次级用户数不变,随着信道数的增多,可获得的网络效益也增加。同时也可以看出,离散量子粒子群优化算法获得的平均最大网络效益在信道数增多的情况下仍然高于其他4种算法。
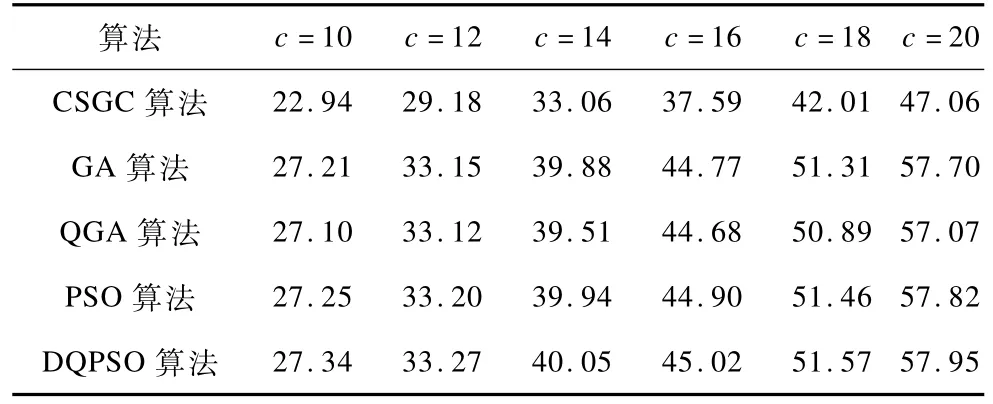
表1 信道数增加时的平均最大网络效益
保持主用户数为10,信道数为10不变,逐渐增加次级用户数u,通过仿真研究平均最大网络效益的变化,得到结果如表2所示。可以看出,主用户数及信道数不变,随着次级用户数的增多,由于次级用户间的竞争更加激烈,从而产生更多干扰,因此可获得的网络效益随之减少。同时可以看出,离散量子粒子群优化算法获得的平均最大网络效益在次级用户数增多的情况下仍然高于其他4种算法。
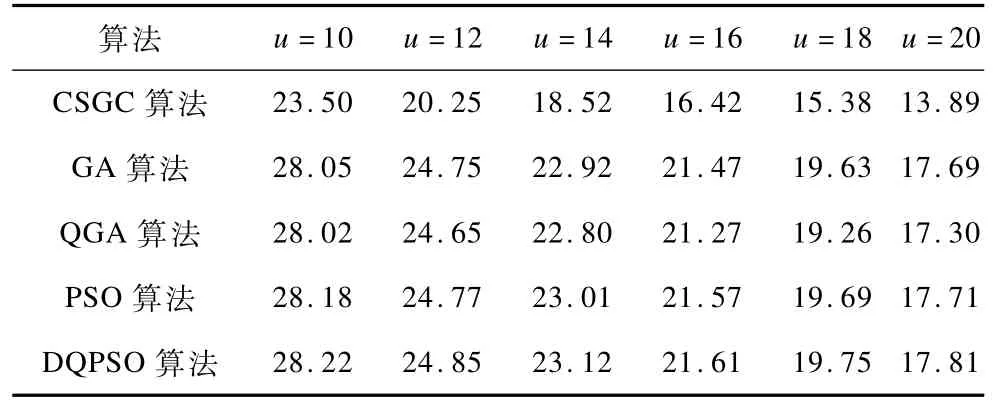
表2 次级用户数增加时的平均最大网络效益
5.2 基于最大比例公平网络效益的仿真实验
设置主用户数为20,可用信道数为20,次级用户数为10。仿真结果如图2所示。其中,纵坐标代表算法使用最大比例公平网络效益函数时获得的效益。可以看出尽管GA,QGA,PSO算法具有较快的收敛速度,但都陷入局部最优,而本文的DQPSO算法具有相对较高的收敛精度,300代以后获得的最大比例公平网络效益高于其他算法。
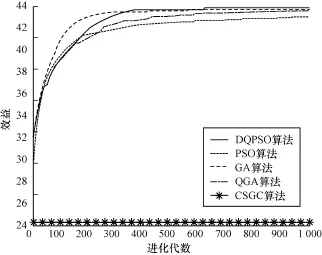
图2 基于最大比例公平网络效益的收敛曲线
保持次级用户数为10不变,逐渐增加信道数c,并使主用户数与信道数相等,通过仿真研究最大比例公平网络效益的变化,得到结果如表3所示。可以看出,离散量子粒子群优化算法获得的最大比例公平网络效益仍然高于其他4种算法,网络效益随信道数增加而增加。
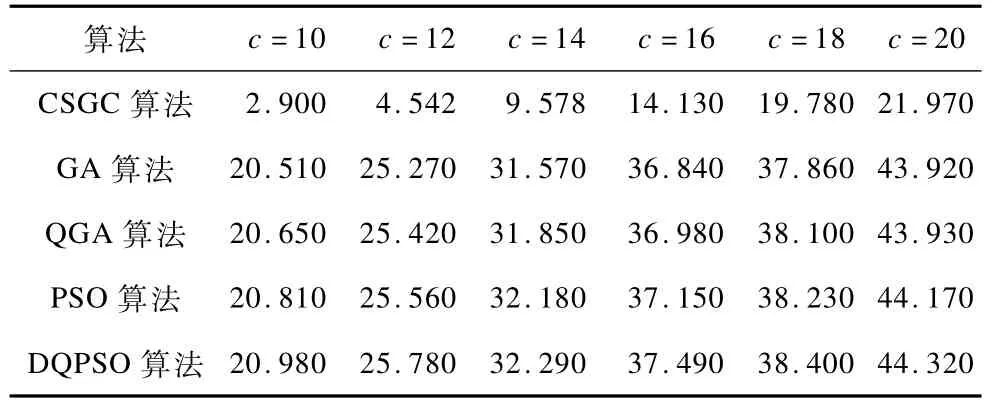
表3 信道数增加时的最大比例公平网络效益
保持主用户数为10、信道数为10不变,逐渐增加次级用户数u,通过仿真研究最大比例公平网络效益的变化,得到结果如表4所示。可以看出,离散量子粒子群优化算法获得的最大比例公平网络效益仍然高于其他4种算法,网络效益随次级用户数增加而减少。
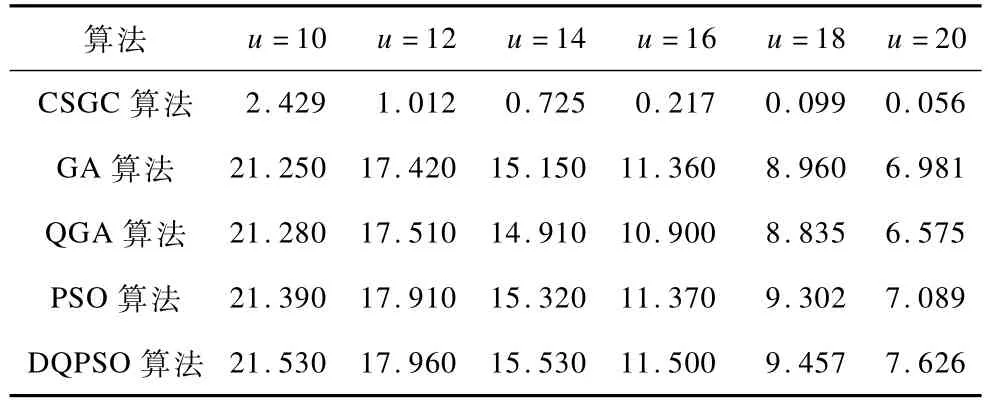
表4 次级用户数增加时的最大比例公平网络效益
6 结束语
为解决认知无线电频谱分配的离散优化问题并提高分配性能,本文提出一种离散量子粒子群优化算法,该算法用量子计算理论更新粒子,可以从平均最大网络效益和最大比例公平网络效益2个方面解决认知无线电频谱分配问题。实验结果表明,相较于传统的CSGC算法和其他经典进化算法,本文算法在2种效益函数下都能有效提高网络效益。下一步工作是将DQPSO算法应用到认知无线电频谱感知等领域。
[1] Liu Zhe,Geng Xiaoyan,Dong Mo.Two Dimension Spectrum Allocation for Cognitive Radio Networks,Wireless Communications[J].IEEE Transactions on Wireless Communications,2014,13(3):1410-1423.
[2] Tragos E Z,Zeadally S,Fragkiadakis A G,et al. Spectrum Assignment in Cognitive Radio Networks:A Comprehensive Survey[J].IEEE Communications Surveys&Tutorials,2013,15(3):1108-1135.
[3] 王中伟,贾振红,覃锡忠,等.基于认知无线电网络的动态频谱分配[J].计算机工程,2014,40(3):127-131.
[4] Haykin S.Cognitive Radio:Brain-em powered Wireless Communications[J].IEEE Journal on Selected Areas in Communications,2005,23(2):201-220.
[5] Zhao Zhijin,Peng Zhen,Zheng Shilian,et al.Cognitive Radio Spectrum Allocation Using Evolutionary Algorithm s[J].IEEE Transactions on Wireless Communications,2009,8(9):4421-4425.
[6] 刘 鑫,谭学治.认知无线电中OFDM多用户频谱分配[J].哈尔滨工程大学学报,2009,30(10):1165-1169.
[7] Peng Chunyi,Zheng Haitao,Zhao Ben.Utilization and Fairness in Spectrum Assignment for Opportunistic Spectrum Access[J].ACM Mobile Networks and Applications,2006,11(4):555-576.
[8] 彭 振,赵知劲,郑仕链.基于混合蛙跳算法的认知无线电频谱分配[J].计算机工程,2010,36(6):210-212,217.
[9] 柴争义,刘 芳.基于免疫克隆选择优化的认知无线网络频谱分配[J].通信学报,2010,31(11):92-100.
[10] Kolodzy P J.Interference Temperature:A Metric for Dynamic Spectrum Utilization[J].International Journal of Network Management,2006,16(2):103-113.
[11] Wang Beiwei,Wu Yongle,Liu K JR.Game Theory for Cognitive Radio Networks:An Overview[J].Computing Networks,2010,54(14):2537-2561.
[12] Am iri B,Fathian M,Maroosi A.Application of Shuffled Frog-leaping Algorithm on Clustering[J].International Journal of Advanced Manufacturing Technology,2009,42(1/2):199-209.
[13] Gao Hongyuan,Liu Yuqi,Diao Ming.Robust Multi-user Detection Based on Quantum Bee Colony Optimization[J].International Journal of Innovative Computing and Applications,2011,3(3):160-168.
[14] Eusuff M,Lansey K,Pasha F.Shuffled Frog-leaping Algori-thm:A Memetic Meta-heuristic for Discrete Optimization[J].Engineering Optimization,2006,38(6):129-154.
[15] Gao Hongyuan,Diao Ming.Quantum Particle Swarm Optimization for MC-CDMA Multiuser Detection[C]// Proceedings of International Conference on Artificial Intelligence and Computational Intelligence.Washington D.C.,USA:IEEE Press,2009:132-136.
[16] Gao Hongyuan,Cao Jinlong,Diao Ming.A Simple Quantum-inspired Particle Swarm Optimization and Its Application[J].Information Technology Journal,2011,10(12):2315-2321.
编辑金胡考
Cognitive Radio Spectrum Allocation with Discrete Quantum-behaved Particle Swarm Optimization
DIAO Ming,ZHANG Zhiqiang,GAO Hongyuan
(College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China)
In order to solve discrete optimization problem in Cognitive Rradio(CR)spectrum allocation and improve the allocation performance,this paper proposes a Discrete Quantum-behaved Particle Swarm Optimization(DQPSO)algorithm.It updates the particles with quantum computing theory and adjusts the rotation angle with wave function,and it has both advantages of fast convergence rate of Particle Swarm Optimization(PSO)algorithm and high precision of quantum Computing.W hen applied in the problem of CR spectrum allocation,it can improve the performance of spectrum allocation effectively.This paper com pares the performance of the proposed algorithm with the Genetic Algorithm(GA),Quantum-inspired Genetic Algorithm(QIGA),PSO algorithm and Color Sensitive Graph Coloring(CSGC)algorithm in different network benefit functions.Simulation results show that the proposed algorithm can search faster for the optimal solution,and it has better performance.
Cognitive Radio(CR);spectrum allocation;discrete optimization;Discrete Quantum-behaved Particle Swarm Optimization(DQPSO)algorithm;network benefit function
刁 鸣,张志强,高洪元.离散量子粒子群优化的认知无线电频谱分配[J].计算机工程,2015,41(11):126-130.
英文引用格式:Diao Ming,Zhang Zhiqiang,Gao Hongyuan.Cognitive Radio Spectrum Allocation with Discrete Quantum-behaved Particle Swarm Optimization[J].Computing Engineering,2015,41(11):126-130.
1000-3428(2015)11-0126-05
A
TP393
10.3969/j.issn.1000-3428.2015.11.022
国家自然科学基金资助项目(61102106);中央高校基本科研业务费专项基金资助项目(HEUCF140809);中国博士后科学基金资助项目(2013M 530148)。
刁 鸣(1960-),男,教授、博士生导师,主研方向:宽带信号检测,处理与识别,通信信号处理;张志强,硕士研究生;高洪元,副教授。
2014-11-17
2014-12-14 E-m ail:diaom ing@hrbeu.edu.cn

