基于多阶马尔可夫预测的个性化推荐算法
韦 炜,全渝娟,卓奕涛,陈学亮,林 艳
(暨南大学信息科学技术学院,广州510632)
基于多阶马尔可夫预测的个性化推荐算法
韦 炜,全渝娟,卓奕涛,陈学亮,林 艳
(暨南大学信息科学技术学院,广州510632)
针对现有推荐系统仅考虑用户兴趣偏移的随机性,而忽略用户兴趣偏移时效性的问题,通过研究马尔可夫模型,并引入滑动时间窗口机制,提出一种新的多阶马尔可夫预测推荐算法。该算法通过学习用户历史行为数据,以及分析用户浏览行为特征,达到准确预测用户浏览行为的目的。实验结果表明,与协同过滤算法相比,该推荐算法不仅能够针对用户兴趣的偏移进行有效预测推荐,而且运行时间较短。
用户兴趣;马尔可夫模型;随机性;时效性;滑动时间窗口;推荐系统
1 概述
随着互联网的发展与普及,海量的信息正在社会的每一个角落中蔓延。互联网为用户带来便捷服务的同时,也使得用户无法从海量的信息中找到对自己真正有用的信息,降低了信息的利用率,这即是“信息超载”问题。
传统的搜索引擎往往只能给所有用户呈现相同的搜索结果,为了更加精准地向用户提供感兴趣的信息,推荐系统应运而生[1]。推荐系统作为一种信息过滤的重要手段,是当前解决“信息超载”问题的最有效的方法之一[2-3]。推荐系统通过对用户历史浏览记录等因素的分析,预测用户的兴趣偏好,向用户推荐商品和服务[4]。与传统搜索引擎不同,推荐系统通过对用户历史行为数据的分析,向用户提供个性化推荐。
推荐系统的应用领域非常广泛,涵盖电子商务、电影、音乐、视频、广告、社交网络等诸多领域。其中,新闻推荐系统是当前最热门的推荐系统之一。在日常生活中,人们可以通过互联网获取各种类型的新闻,如财经新闻、娱乐新闻以及体育新闻等。因此,根据用户兴趣或偏好的不同,用户感兴趣的新闻也会各自不同。如何通过推荐系统帮助用户发现和提取其真正感兴趣的新闻成为目前推荐系统研究的一个热点。现实生活中,用户的偏好时常随着个人兴趣的转变而改变。研究结果表明,用户的偏好会在新事物的刺激下不断地发生变化[5]。此外,随着时间的推移,个人偏好也会产生变化。因此,将新闻和用户兴趣动态变化的特性引入研究中,将有助于发现用户兴趣偏移的规律,提高新闻推荐的准确性。
如果将新闻动态特征的研究与用户浏览新闻的随机行为进行关联,建立有效的用户浏览预测模型,通过提取用户浏览过程中反映出的个性化特征及用户兴趣的动态变化,发现用户兴趣偏移的规律,将有利于推荐系统更加准确地对用户浏览行为进行预测。
马尔可夫模型是一种动态随机模型[6]。而用户浏览新闻是一个受浏览目的、兴趣爱好、文化背景等多种因素影响的动态随机过程。因此,可以通过引入马尔可夫模型记录用户的新闻浏览过程,并依据其紧邻的状态实现动态预测推荐。文献[7]首先将马尔可夫模型应用于日志挖掘,通过对用户浏览过程的抽象,建立简单有效的用户浏览行为预测模型;文献[5]利用马尔可夫模型通过用户历史记录学习用户的偏好模式,发现用户偏好会随着时间的推移而产生变化;文献[8]通过分析用户历史浏览记录,利用马尔可夫模型预测用户对产品的倾向性。为了解决现实生活中电子商务产品推荐问题,文献[9]利用马尔可夫链跟踪用户的购买行为,运用时间分集增强电子商务推荐的时间多样性。文献[10]基于马尔可夫动态模型提出了一种融合停留时间的推荐模型。该模型利用停留时间来描述用户对某一偏好的感兴趣程度及所推荐网页的重要性。然而,以上模型仅仅考虑了用户浏览行为的随机性,并未考虑该行为的时效性。时效性指用户在一定时间内查阅的所有信息对决策均有一定价值。例如,在新闻推荐系统中,用户在一定时间段内阅读的所有新闻,均可表示用户在该段时间内的兴趣偏好。研究结果表明,在新闻推荐系统中,对时效性问题的研究能够记录用户兴趣的偏移,提高推荐的准确性[11-12]。因此,设计基于用户浏览行为的动态预测推荐模型时应考虑时效性的影响。
本文考虑马尔可夫模型对动态预测推荐模型研究的积极效用,提出一种多阶马尔可夫预测模型(Multi-step Markov Predict Model,MMPM),并基于该模型提出多阶马尔可夫预测推荐算法(Personalized Recommendation Algorithm Based on Multi-step Markov Predict,MMPA)。该算法在考虑用户浏览随机性和时效性的情况下,通过建立转移概率矩阵得到候选推荐列表,并进行个性化推荐。
2 数学模型及问题描述
2.1 多阶马尔可夫预测模型
本文采用有向图对MMPM进行描述。考虑在新闻推荐中,用户阅读新闻i之后点击阅读新闻j,就可能代表着一次兴趣的转移,因此将MMPM的一次状态转移作为一次事件,代表用户关注点和兴趣的偏移。
图1为多阶马尔可夫预测模型示意图。

图1 多阶马尔可夫预测模型示意图
其中,V为顶点集,表示状态,例如在新闻推荐中,顶点集V是由新闻集组成,如果用户处于状态v1,则表示用户当前阅读的新闻为v1;E为边集,记录用户浏览记录中的所有状态转移,e12表示为用户浏览行为从状态v1到状态v2的转移,即用户阅读新闻v1之后点击新闻v2;NE为边的连接次数的集合,的数值表示为状态v1到状态v2的一阶转移次数,以此类推,的数值表示为状态v1到状态v2的d阶转移次数;用户状态的一次转移就可能代表着用户兴趣的一次偏移。因此,在运用多阶马尔可夫预测模型进行推荐时,依照用户浏览的信息建立顶点集V;根据用户历史浏览记录建立边集E,运用来表示边的用户状态的d阶转移次数;PE是由K×K(K表示顶点集V元素个数)生成的转移概率矩阵,例如P12为状态v1转移到状态v2的条件转移概率。每条边eE上标注有状态的连接次数和转移概率PE。
基于此,多阶马尔可夫预测模型可以形式化描述为:
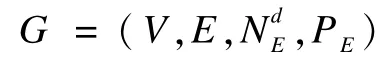
其中,V=(v1,v2,…,vK)是顶点集,顶点用于表示状态,|V|=K;E={eij|i∈V,j∈V}是边集,边用于表示状态转移;NdE∈[0,N]是一个函数,它给每条边e=(i,j)∈E赋予数值,用于表示顶点i到顶点j的一阶转移次数,以此类推,表示为顶点i到顶点j的d阶转移次数;PE∈[0,1]是一个函数,它给每条边e=(i,j)∈E赋予一个条件存在概率Pe∈(0,1)用于表示顶点i和j之间实际存在的条件下,由顶点i转移到顶点j的转移概率。
2.2 数学模型
2.2.1 马尔可夫链
设有随机过程序列{Xn,n∈1,2,…}的状态空间V是离散的过程Xn=Xn(tn)所处的状态为:x1,x2,…,xn的其中一个,对于任意时刻tn,下面的条件概率公式成立:
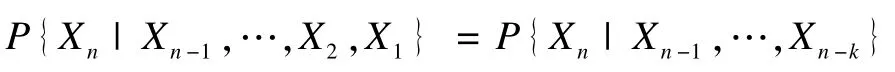
则称序列{Xn,n∈1,2,…}满足k阶马尔可夫模型。
在处理实际问题时,通过引入转移概率[13]表示系统状态间的转移情况:
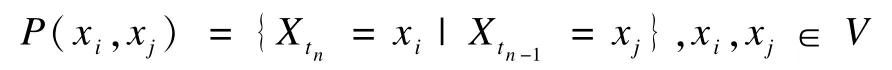
上式中转移概率表示:已知在时刻tn-1系统的状态处于xj的条件下,在tn时刻系统的状态处于xi的条件概率。
在离散时间变量条件下,可以得到如下形式[14]:
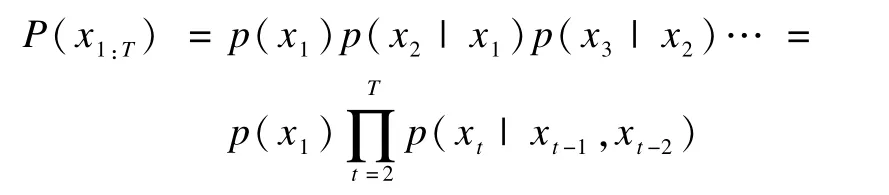
假设所有观察到的变量是离散的,所以{xn,n∈1,2,…}可称为离散状态或有限状态的马尔可夫链。2.2.2 基于马尔可夫模型的最大似然估计
假设存在一个浏览序列数据集D=(X1,X2,…,XN),其中,Xi=(xi1,xi2,…,xi,Ti),i∈1,2,…代表用户i的浏览序列,在取得样本为x1:T的条件下,模型参数用θ表示,要求使用最大似然估计得到最优参数,使得似然函数的值最大,以下是单用户浏览数据的似然函数[13]。
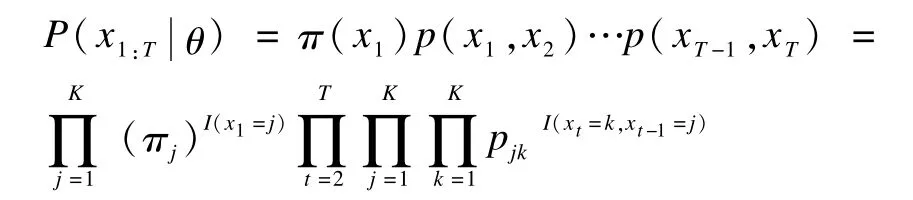
其中,π(x1)=p(x1);I(x)为示性函数。同时定义以下等式:
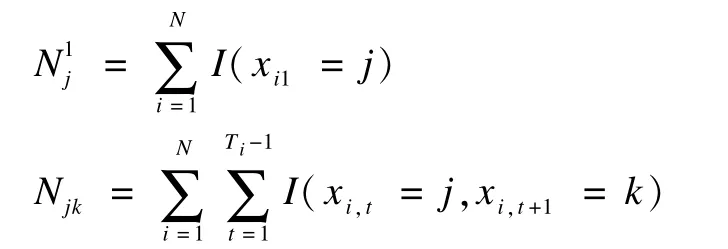
假设用户的浏览行为是相互独立的,则存在数据集的对数似然函数如下:
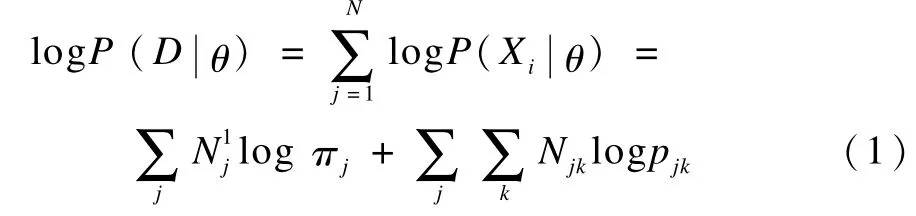
式(1)存在以下优化问题:
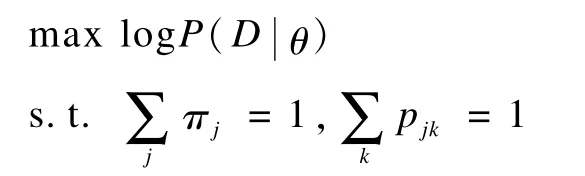
其中,j∈1,2,…,K。
可得拉格朗日函数:
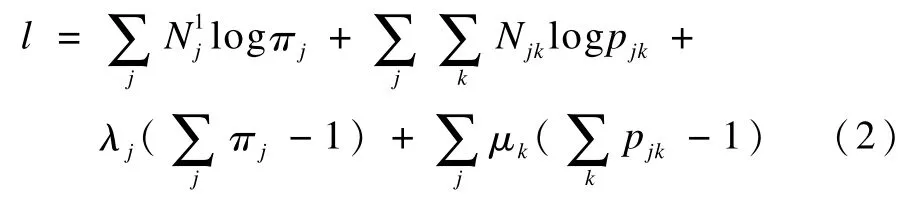
其中,λj>0;μk>0。
由式(2)可以得到对数似然方程组:
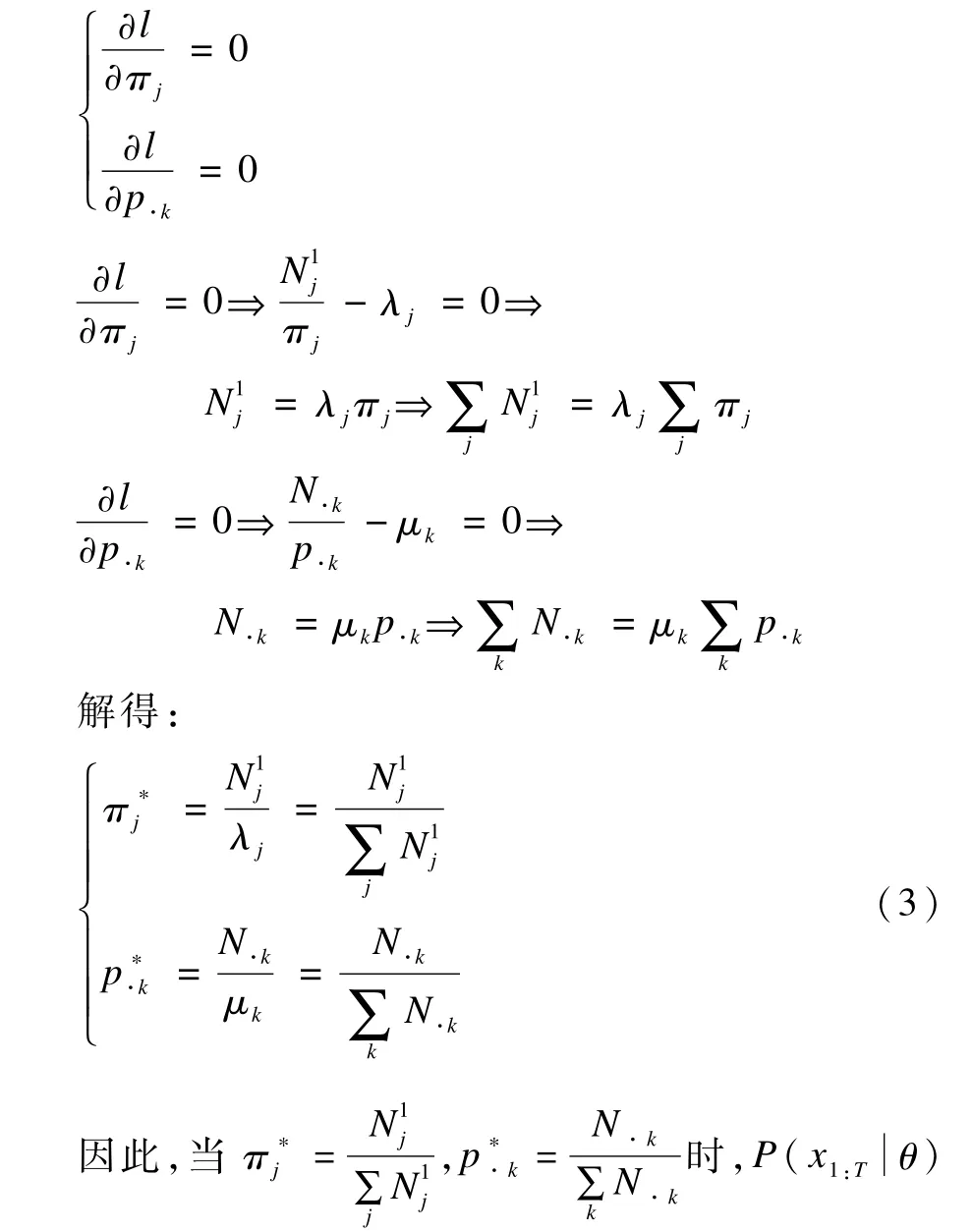
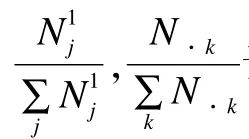
2.3 多阶马尔可夫预测推荐算法
图2为用户浏览顺序示意图。考虑数据时效性、浏览随机性等因素,用户到状态v4的转移可能受到状态v1,v2甚至其他用户历史状态的影响。本文提出了基于多阶马尔可夫预测模型的个性化推荐算法,该算法正是充分考虑了用户浏览记录(状态)蕴含的用户偏好信息。如就单一用户个体考虑,在短时间内,其兴趣偏好不会发生太大变化。如图2所示,用户1从状态v1转移到状态v2,即v1→v2,则代表着用户1兴趣的一次一阶转移,此次状态的转移记入v1→v2的一阶转移次数N112;如果在短时间内发生了用户从状态v1经过状态v2到状态v4的转移,即v1→v2→v4,则考虑v1→v4的转移是用户兴趣偏移的一次二阶转移,此次状态的转移记入v1→v4的二阶转移次数。
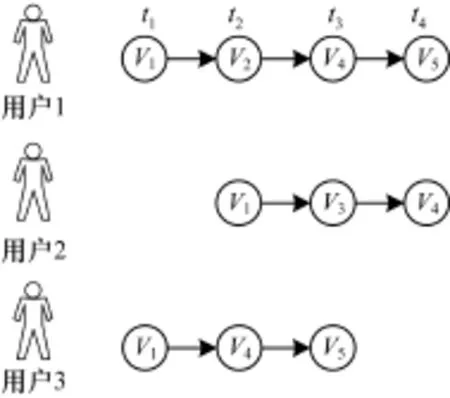
图2 用户浏览顺序示意图
MMPA的实现主要由MMPM建模和推荐预测两大部分组成。其中,MMPM建模包括:(1)根据数据时效性设置时效性参数Δt;(2)计算每个状态的一阶转移次数和一阶转移概率;(3)计算每个状态的多阶转移次数和多阶转移概率;(4)求取每个状态的转移概率。推荐预测则包括:(1)生成当前时刻的转移概率矩阵;(2)预测用户的偏好;(3)实施个性化推荐。MMPA实现示意如图3所示。
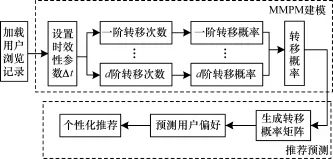
图3 MM PA实现示意图
3 多阶马尔可夫预测推荐算法设计
3.1 时效性问题
对一个给定用户作推荐时,若依赖之前过于陈旧的状态去推演用户当前的偏好,在推荐预测效果方面可能会大打折扣。因此,本文针对推荐中存在的信息(状态)时效性的问题,引入滑动时间窗口为时效性约束条件。图4为滑动时间窗口示意图。
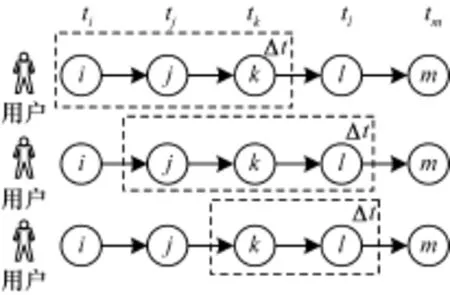
图4 滑动时间窗口示意图
本文将滑动时间窗口大小设置为Δt。如图4所示,滑动时间窗口的滑动过程可以描述如下:
(1)时刻ti,此时,滑动时间窗口内的状态i,j,k均可能蕴含时刻ti用户的偏好信息。时刻ti的滑动时间窗口包含以下3种情况:1)状态i到状态j为状态i的一阶状态转移,因为t,所以此次状态i到状态j的一阶状态转移计入状态i到状态j的一阶转移次数2)状态i到状态k为状态i的二阶状态转移,因为,所以状态i到状态k的二阶转移计入状态i到状态k的二阶转移次数特别地,在时刻ti存在,即状态l不在时刻t i的滑动时间窗口内,因此状态i到状态l的三阶状态转移将不计入状态i到状态l的三阶转移次数。
(2)当滑动时间窗口随时间滑动到时刻tj时,此时且,在滑动时间窗口滑动的过程中,状态i被移出滑动时间窗口,同时新的状态l进入滑动时间窗口,状态m不进入滑动时间窗口,因此,时刻tj滑动时间窗口内的状态包含j,k,l,状态j到状态k为状态j的一阶状态转移,状态j到状态l为状态j的二阶状态转移。
3.2 转移概率
3.2.1 MMPM一阶转移概率
用户在时刻ti的状态为i,在时刻ti的滑动时间窗口Δt内,用户状态从状态i一阶转移到状态j。由基于马尔可夫模型最大似然估计和式(3),可以计算时,用户浏览记录中由状态i一阶转移到状态j的一阶转移概率:
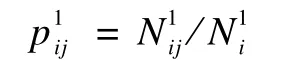
3.2.2 MMPM多阶转移概率
如果用户在任意时刻滑动时间窗口Δt内进行了多次状态转移,则用户在该时刻的滑动时间窗口内所有状态转移均可以代表着用户在该时刻的兴趣偏好,因此考虑用户兴趣状态一阶转移的同时,也需要考虑状态的多阶转移情况,状态的多阶转移也代表着用户在该时刻的兴趣偏好。状态多阶转移示意图如图5所示。
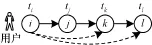
图5 状态多阶转移示意图
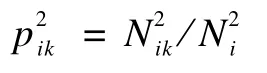
3.2.3 转移概率矩阵
假设状态i和状态j均为用户在某时刻滑动时间窗口Δt内的兴趣偏好,由于用户浏览顺序的不同,当时,状态i可能一阶转移到状态j,也可能多阶转移到状态j。考虑时效性影响,在计算转移概率时,应同时考虑在滑动时间窗口内,每个状态进行转移的一阶转移概率和多阶转移概率。
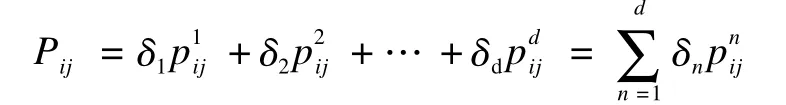
最后由转移概率可构成转移概率矩阵,表示为:

3.3 推荐预测
根据转移概率矩阵,可以计算每个用户下一时刻最有可能转移到的状态。在推荐预测时,有些状态转移可能来自于用户的失误操作,因此本文设置转移概率阈值Δp用于排除数据噪声。推荐预测示意图如图6所示。
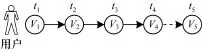
图6 推荐预测示意图
假设下一时刻为t5,根据转移概率矩阵可以预测用户在时刻t5从状态v4转移到其他状态中转移概率最高的状态,排除用户已经转移的状态(v1,v2,v3,v4),因此转移概率矩阵中由状态v4转移到其他状态中转移概率最高且满足转移概率阈值的状态即为用户下一时刻最有可能转移到的状态。以此类推,可以预测出所有用户在下一时刻可能转移到的状态。为了形式化描述候选推荐列表,以符号List(max)来表示依据转移概率矩阵生成由每个状态转移到其他所有状态中符合条件的状态组成的候选推荐列表,其中List4(max)可表示用户处于状态v4转移到其他所有状态中符合推荐条件的状态组成的候选推荐列表。
3.4 多阶马尔可夫预测算法伪代码
为了解决兴趣偏移的随机性和时效性问题,本文提出多阶马尔可夫预测推荐算法。其算法核心伪代码如下:
输入 H为用户浏览记录的数据集合;U为用户集合;d为兴趣转移阶数;ΔP为转移概率阈值
输出 R为预测下一时刻用户的状态
Step1 计算每阶转移次数(设最高转移d阶)

Step2 计算转移概率,并生成转移概率矩阵
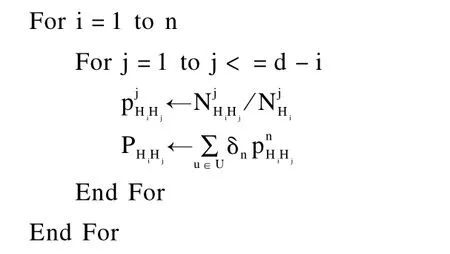
Step3 下一时刻用户状态的候选列表

首先顺序读取所有用户浏览记录,并设置滑动时间窗口Δt。然后依据滑动时间窗口计算状态Hi与其他状态间的一阶转移次数和多阶转移次数。接着根据转移次数计算转移概率PHiHj并生成转移概率矩阵。最后依据转移概率矩阵生成每个用户的候选列表并进行排序。如果候选列表ListHi(max)中的转移概率高于转移概率阈值Δp,则将ListHi(max)中符合推荐策略的新闻推荐给用户Ri。
4 实验结果与分析
4.1 实验数据及实验环境
为了衡量本文提出的多阶马尔可夫预测算法的预测准确性,选取DataCastle网站公开的新闻推荐数据集[15]进行实验。该数据集包含10 000名用户、6 102条新闻和116 225个浏览记录,且每条记录包括用户编号、新闻编号、浏览时间以及新闻文本内容。实验将数据集分为训练集和测试集两部分。其中抽取所有用户浏览的最后一条记录作为测试集,即测试集包含10 000个数据项,而其余数据作为训练集。实验环境为Intel(R)CoreTMi3-2320M CPU@2.4 GHz、8 GB内存、W indow s8主机,编程环境为JDK 1.8。
4.2 实验评价标准
对算法性能进行评估的一项重要原则是评估算法的成功率。因此,本文选取F-Measure指标作为最终的评价指标。
令U为用户数据集合;R(u)为算法依据用户在训练集的行为预测的推荐集合;T(u)为测试集包含的数据。
定义1 准确率(precision)[16],即推荐列表中,用户最终选中的新闻占推荐列表新闻数的比例。
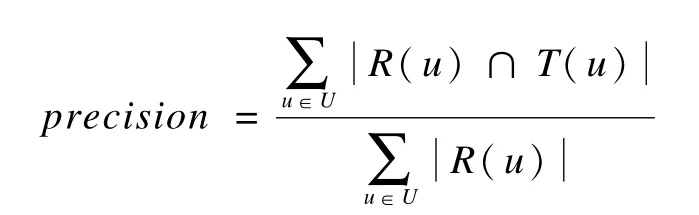
定义2 召回率(recall)[16],即推荐列表中,用户最终选中的新闻占所有用户选中新闻的比例。

定义3 F-Measure[16],准确率和召回率的调和平均数。准确率和召回率是相互制约和矛盾的,F-Measure能够将两者进行综合考虑,带来更为准确的推荐系统性能评价。
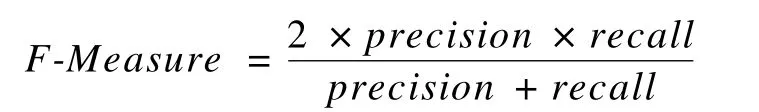
4.3 协同过滤算法
通过计算与当前用户阅读新闻相似度排名前n的用户,预测用户最有可能阅读的下一条新闻。其中,用户集合用Top@n表示。实验结果如表1所示。当计算与用户相似度排名前60的用户,即用户集为Top@60时实验结果最优。
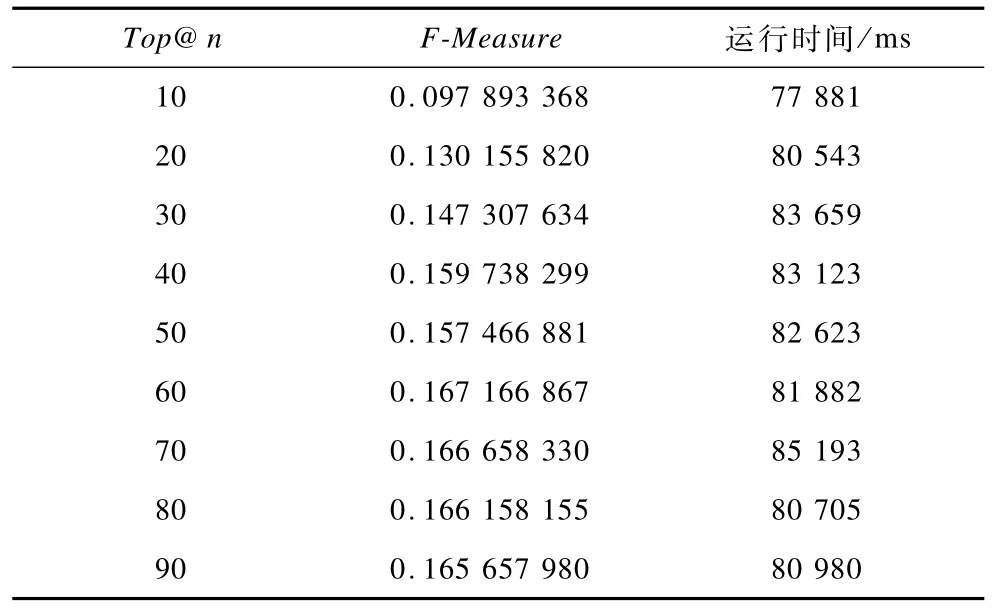
表1 协同过滤算法实验结果
4.4 MM PA实验结果
本文通过实验验证权重系数δn的有效性,并分析引入转移概率阈值、滑动时间窗口等参数后算法的推荐预测效果。通过训练集建立模型,运用MMPA预测用户浏览的最后一条新闻,将预测结果与测试集进行比较,确定在测试集中命中的记录数。
4.4.1 权重系数实验
本文实验的目的是为了证明计算转移概率时,考虑多阶转移概率能够提高推荐预测效果。实验仅考虑用户兴趣偏移的随机性,忽略用户兴趣偏移的时效性,因此将滑动时间窗口Δt设置为无穷大。
表2为权重系数实验结果,权重系数δd取值范围为0.0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0。特别地,δ1=1.0为仅仅考虑一阶马尔可夫转移概率的情况。实验在计算转移概率时转移阶数最高取值为6阶。表2展示了F-Measure排名前20的参数取值情况。其中,6阶转移概率的权重系数δ6在多数情况下为0。因此,针对实验所采用的数据集,在计算转移概率时,将计算5阶转移阶数。
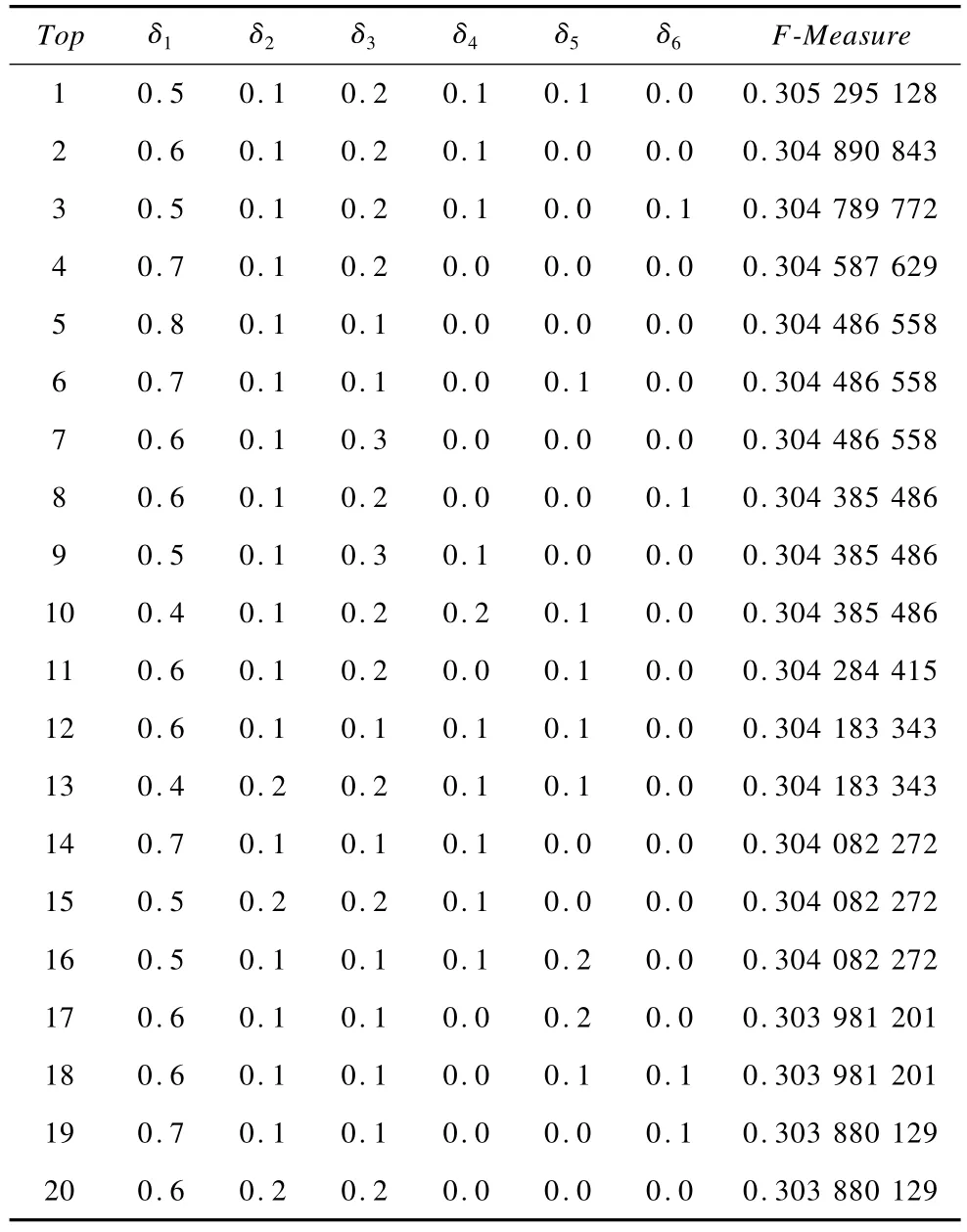
表2 权重系数实验结果
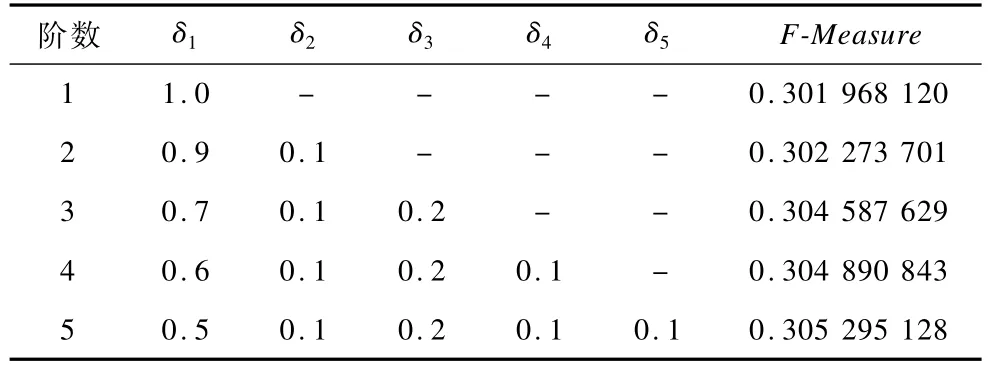
表3 不同阶数预测效果对比
4.4.2 转移概率阈值实验
本文实验目的是为了证明在推荐预测时,考虑转移概率阈值Δp能提高推荐预测效果。
表4为转移概率阈值实验结果。实验转移概率阈值Δp取值为0.0,0.05,0.1,0.15,0.20,0.25,0.30,0.35,0.40。实验计算转移概率时转移阶数最高取值为5阶,表4展示了F-Measure排名前20参数取值情况。其中,转移概率阈值Δp=0.15时,能够得到较优的F-Measure。在表4中,Top2(δ1= 0.7,δ2=0.1,δ3=0.1,δ4=0.1)为考虑四阶转移概率的情况。
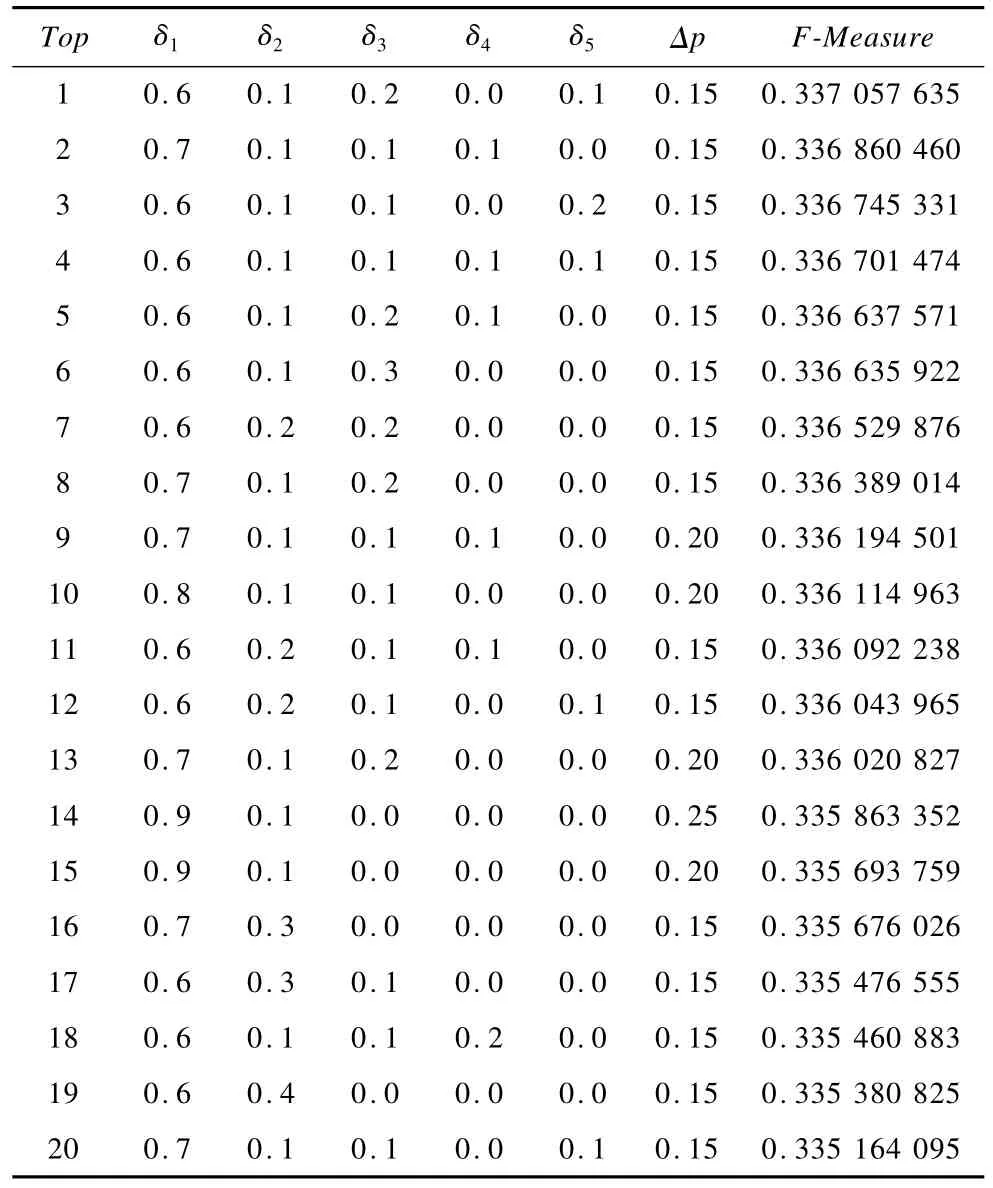
表4 转移概率阈值实验结果
通过对比转移概率阈值实验(表4)与权重系数实验结果(表2),发现考虑转移概率阈值后,实验得到的F-Measure有明显提升。实验结果表明,进行推荐预测时运用转移概率阈值Δp过滤数据噪声能得到更好地推荐预测效果。
图7为一阶与四阶在不同转移概率阈值下实验结果的对比。其中一阶情况下权重系数δ1=1.0,四阶情况下权重系数δ1=0.7,δ2=0.1,δ3=0.1,δ4= 0.1。从图7可以发现四阶的预测效果优于一阶的预测效果,同时可以发现随着转移概率阈值的增长,F-Measure指标会有所下降。这种情况产生的原因是随着转移概率阈值的增长,转移概率矩阵中满足转移概率阈值的新闻会减少,虽然准确率会有明显提升,但可提交的推荐新闻数大幅减少致使召回率明显下降,最终导致F-Measure指标下降。
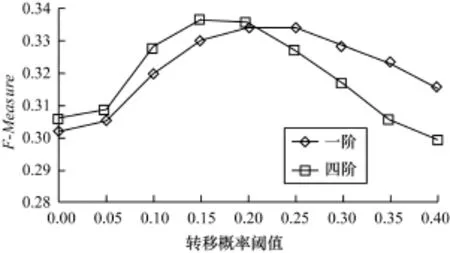
图7 一阶与四阶转移概率阈值对比实验结果
4.4.3 滑动时间窗口实验
本文实验目的是评估时效性对推荐预测的影响。首先,验证引入时效性约束条件后,算法的推荐预测效果。实验将滑动时间窗口设为固定值,滑动时间窗口Δt取值范围为100 s~2 000 s,实验结果如表5所示。实验结果展示了F-Measure排名前20的参数取值情况。如表5所示,Top3(δ1=0.9,δ2= 0.1)为考虑二阶滑动时间窗口的情况。通过滑动时间窗口实验(表5)与转移概率阈值实验(表4)的对比,发现引入时效性约束条件能够有效提升推荐预测效果。实验结果表明,引入滑动时间窗口能够有效地提高推荐预测效果。
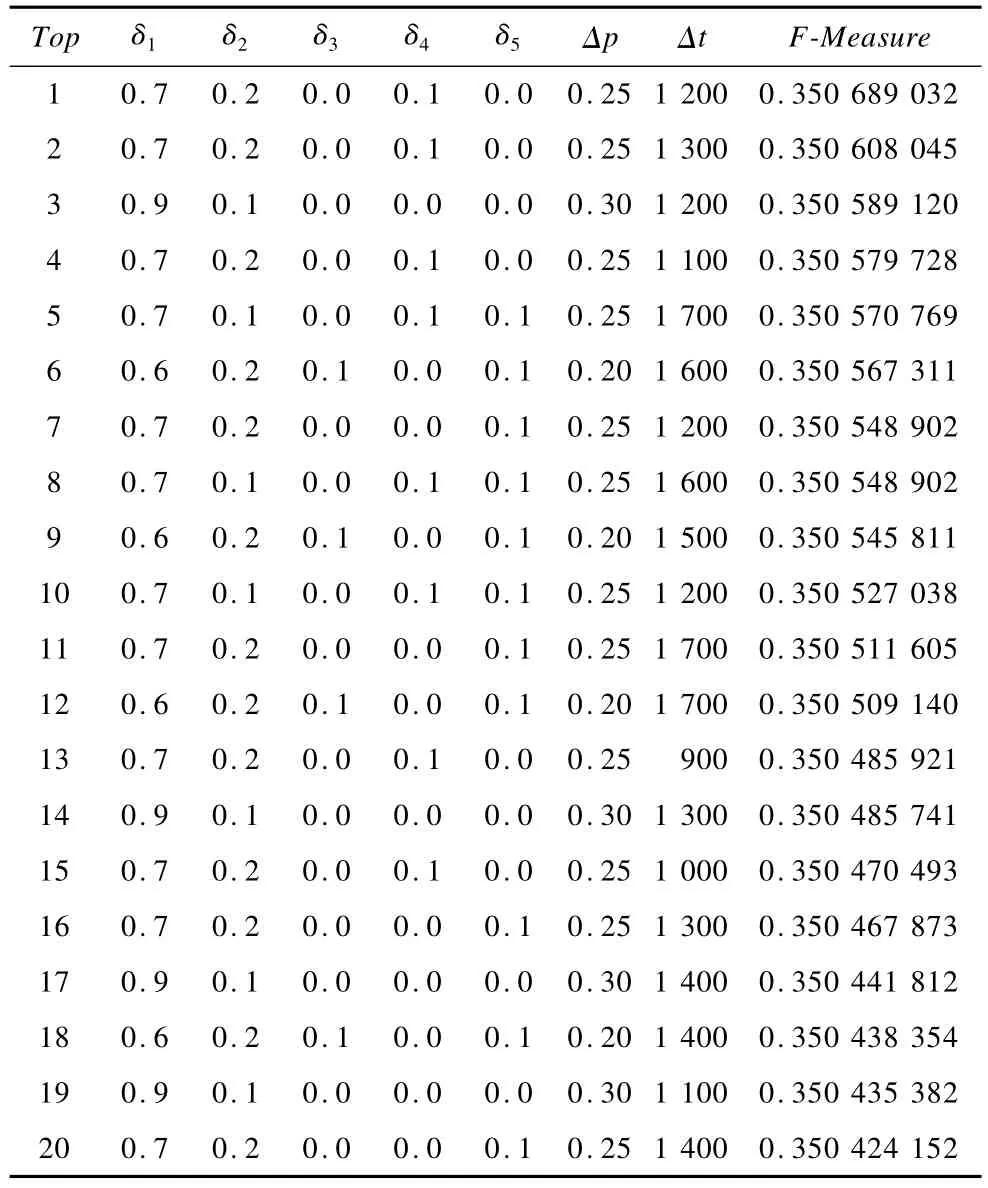
表5 滑动时间窗口实验结果
图8描述了在滑动时间窗口取值不同的情况下,一阶与二阶实验结果的对比情况。其中一阶情况下权重系数δ1=1.0,转移概率阈值Δp=0.3。二阶情况下权重系数δ1=0.9,δ2=0.1,转移概率阈值Δp=0.3。图8表明考虑多阶转移概率可以得到比考虑一阶转移概率更好的预测效果。
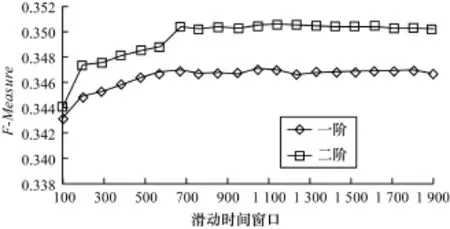
图8 滑动时间窗口对比实验结果
4.4.4 不同方法的推荐结果比较
表6表示2种方法实验结果取值最优的推荐结果比较。协同过滤算法在Top@60得到最优结果。MMPA在权重系数δ1=0.9,δ2=0.1,转移概率阈值Δp=0.3的情况下得到最优结果。表6表明本文提出的MMPA相较于协同过滤算法具有较好的预测推荐效果,尤其在运行时间方面,优势更为明显。

表6 不同算法推荐结果比较
5 结束语
本文通过分析用户浏览新闻产生的历史浏览记录,对用户的浏览兴趣偏好进行建模,并结合传统的马尔可夫模型,提出一种新的多阶马尔可夫预测推荐模型。基于该模型提出了多阶马尔可夫预测推荐算法,并在实际数据集上进行了比较实验。实验结果表明,本文提出的算法能对用户下一条浏览记录进行较为有效的预测推荐。通过算法比较表明,MMPA算法具有更好的推荐预测效果和更短的运行时间。但算法中存在很多不足,比如用户浏览内容、新闻受欢迎程度等因素没有考虑在算法中,算法仍不能准确反映出用户关注新闻的内容和用户对新闻的满意程度。考虑到新闻的时效性和时新性,在选取用户历史浏览记录时,选取历史记录时间跨度较大会造成预测不准确、加载数据过多等问题,例如,选取一定时间内的用户历史浏览记录作为当前新闻推荐依据,能够减少加载数据量。所以,在选取用户历史浏览记录时,也需要考虑历史浏览记录的时效性问题。因此,在今后的研究工作中将考虑用户浏览内容等信息,以及用户历史浏览记录时效性等问题,进一步提高推荐预测的准确度和效率。
[1] 刘建国,周 涛,汪秉宏.个性化推荐系统的研究进展[J].自然科学进展,2009,19(1):1-15.
[2] 许海玲,吴 潇,李晓东,等.互联网推荐系统比较研究[J].软件学报,2009,20(2):350-362.
[3] Awad M A,Khalil I.Prediction of User's Web-brow sing Behavior:Application of Markov Model[J].IEEE Transactions on System s,M an,and Cybernetics,Part B:Cybernetics,2012,42(4):1131-1142.
[4] Resnick P,Varian H R.Recomm ender System s[J]. Communications of the ACM,1997,40(3):56-58.
[5] Sahoo N,Singh P V,Mukhopadhyay T.A Hidden Markov Model for Collaborative Filtering[J].Management Information Systems,2012,36(4):1329-1356.
[6] Kukhtarev N V,Markov V B,Odulov S G,et al. Holographic Storage in Electrooptic Crystals:I.Steady State[J].Ferroelectrics,1978,22(1):949-960.
[7] Zukerman I,A lbrecht D W,Nicholson A E.Predicting Users' Requests on the WWW[C]//Proceedings of the 7th International Conference on User Modeling.Banff,Canada:[s.n.],1999:216-222.
[8] He M,Ren C,Zhang H.Intent-based Recommendation for B2C E-commerce Platforms[J].IBM Journal of Research and Development,2014,58(5/6):1-5.
[9] Gu W,Dong S,Zeng Z.Increasing Recommended Effectiveness with Markov Chains and Purchase Intervals[J].Neural Computing and Applications,2014,25(5):1153-1162.
[10] 刘胜宗,樊晓平,廖志芳,等.融合停留时间的隐Markov个性化推荐模型[J].通信学报,2014,35(9):112-121.
[11] Li L,Zheng L,Yang F,et al.Modeling and Broadening Temporal User Interest in Personalized New s Recommendation[J].Expert System s with Applications,2014,41(7):3168-3177.
[12] 杨兴耀,于 炯.基于信任模型填充的协同过滤推荐模型[J].计算机工程,2015,41(5):6-13.
[13] Chung K L.Markov Chains with Stationary Transition Probabilities[M].Berlin,Germany:Springer,1960.
[14] Murphy K P.Machine Learning:A Probabilistic Perspective[M].Cambridge,USA:M IT Press,2012.
[15] 用户浏览新闻的模式分析及个性化新闻推荐[EB/OL].[2015-03-01].http://www.115.28.182.124/c/0000000005 0/data.
[16] Büttcher S,Clarke C L,Cormack G V.Information Retrieval:Implementing and Evaluating Search Engines[M]. Cambridge,USA:M IT Press,2010.
编辑 索书志
Personalized Recommendation Algorithm Based on Multi-order Markov Prediction
WEI Wei,QUAN Yujuan,ZHUO Yitao,CHEN Xueliang,LIN Yan
(College of Information Science and Technology,Jinan University,Guangzhou 510632,China)
The current research on the recommendation system just considers the randomness too much but ignores the point of timeliness.This paper proposes a new multi-order Markov predicting recommendation system based on the traditional standard Markov model.The algorithm can make up for the deficiency of timeliness by using the new sliding time window mechanism.The algorithm can achieve the mission of accurate prediction about user's browsing activity according to the study of the history data and the analysis of user's brow sing habits.Experimental results show that compared with the collaborative filtering scheme,the new proposed algorithm can provide the predicting recommendation efficiently and effectively judging by the user's interest shift behavior.
user interest;Markov model;randomness;timeliness;sliding time window;recommendation system
韦 炜,全渝娟,卓奕涛,等.基于多阶马尔可夫预测的个性化推荐算法[J].计算机工程,2015,41(11):59-66.
英文引用格式:Wei Wei,Quan Yujuan,Zhuo Yitao,et al.Personalized Recommendation Algorithm Based on Multi-order Markov Prediction[J].Computer Engineering,2015,41(11):59-66.
1000-3428(2015)11-0059-08
A
TP391
10.3969/j.issn.1000-3428.2015.11.011
广东省产学研基金资助项目(2013B090500030);广州市科技攻关计划基金资助项目(2014Y 2-00133)。
韦 炜(1987-),男,硕士研究生,主研方向:机器学习,数据挖掘;全渝娟(通讯作者),副教授、博士;卓奕涛,本科生;陈学亮、林 艳,硕士研究生。
2015-05-28
2015-06-18 E-m ail:josiah.wei@qq.com

