基于监控数据的M ySQL异常检测算法

凌 骏，尹博学，李 晟，王 鑫

（1.天津大学计算机科学与技术学院，天津300072；2.百度（中国）有限公司，北京100085）

基于监控数据的M ySQL异常检测算法

凌 骏1，2，尹博学2，李 晟2，王 鑫1

（1.天津大学计算机科学与技术学院，天津300072；2.百度（中国）有限公司，北京100085）

随着互联网数据规模的增长，服务器集群的规模快速扩大，对大规模的集群进行监控和分析成为互联网行业运维的难点。为此，根据监控统计数据剧烈波动的特点，提出一种M ySQL异常检测分析算法，采用基于模式的异常检测方法，无须设置阈值，分段取模式特征值，计算异常点、异常区间和异常程度。实验结果表明，该算法对于抖动剧烈监控数据的时序序列可以较好地提取数据特征，与基于均值方差的异常检测算法相比，具有更高的精准度，对监测数据的适用性较强。

异常检测；监控数据；统计；模式；时间序列

1 概述

基于监控统计数据的异常检测是对各类系统的大量监控数据进行分析，实现监控自动化、进行预测报警、定位问题的基本方法。随着系统规模的快速扩增，监控数据的规模也随之增长。如何结合统计学原理，对大规模的监控数据进行分析，给出系统问题的定位建议，成为一个很有价值的问题。一个可以自动对大规模监控数据进行自动分析，并且可以对问题的定位提供建议的异常检测模型，可以大大降低运维成本，提高工作效率。

传统的异常检测方法主要有：基于分布的方法［1］，基于深度的方法［2-3］，基于聚类的方法［4］，基于距离的方法［5］和基于密度的方法［6-7］。基于分布和深度的方法要求已知数据集的分布，根据观察结果是否符合分布确定是否为异常数据，显然对于抖动剧烈的监控数据不可能预知其分布；基于聚类的方法一定程度上可以进行异常分析，由于效率问题一般不用于此场景；基于距离和密度的算法对于内部密度明显的数据集会遇到问题，或者局部都判断为异常，或者无法发现。

在经济学领域，尤其是在证券交易等方面，统计学家建立了自回归滑动平均模型（Auto-Regressive and Moving Average model，ARMA）［8］等成熟的数学模型对时序数据进行建模，可以很好地拟合季节性趋势和随机因素，对某一时刻之后较短的时间段进行预测，并且给出置信区间。但是对于监控数据，数据的抖动非常剧烈，系统故障和人为因素都会导致监控数据的变动，不具备固定的周期性。且当系统发生故障时，无法定位具体的时间点。ARMA等传统的模型对数据要求较高，且只能预测某一时间点后一小段时间的值。这些模型在拟合较长期的周期性数据时可以达到不错的效果，而在系统的监控数据方面效果并不理想。

本文提出一种基于监控数据的M ySQL异常检测算法，该算法基于模式的聚类算法［9-10］，分段取模式特征，结合k最近邻（k Nearest Neighbor，kNN）［11］算法，计算局部异常因子。

2 基于模式的异常检测方法

通过等时间间隔收集系统状态，可以得到系统状态相关的时间序列。时间序列的异常按照其形式，可以分为序列异常、点异常和模式异常。

在异常检测领域，所谓模式指的是将数据按照一定规则进行划分，然后根据数据特性，对每个分片计算相关的统计量，作为此分片的特征值。多维特征值构成一个向量，也称之为模式，用于描述此分片的主要统计特性：

（1）序列异常。对于大量时间序列，某个序列在均值、方差等特征方面明显不同于其他序列，称之为序列异常。

（2）点异常。在某一条时间序列中，部分点明显偏离整体序列的趋势，称之为点异常。

（3）模式异常。对时间序列进行模式化，序列中部分子序列的模式特征明显不同于绝大多数其他子序列的模式特征，称之为模式异常。

本文通过对时间序列进行划分，采集各模式特征，计算并定位异常的模式所在区间，给出模式异常程度。

2.1 监控数据场景分析

M ySQL集群的监控，每隔相等的时间段对系统和数据库各统计项进行采集，可以获取到大量的监控数据的时间序列。由于监控数据的多样性，针对不同的数据特征，需要采用不同的方法进行分析。本文提出的方法主要针对无规律的、剧烈波动的序列进行检测。无需手动设置阈值，只根据数据本身的特征，找到其中的异常区间，给出异常程度。

2.1.1 线上监控数据特点

异常数据的检测，针对图1所示的数据，横坐标为时间轴，纵坐标为具体的数值，从280时刻开始到350左右，这段数据和其他绝大多数时间段区别较大。针对这种数据，提出了一个算法，找到异常区间并且给出异常程度。

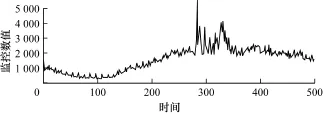
图1 M ySQL的某个监控项时序图

如图1所示异常主要有2点特性：

（1）部分子序列有偏离大多数子序列的趋势；

（2）异常已经发生，隐藏于序列之中，需要寻找异常模式，给出异常程度。

2.1.2 监控数据归类分析

不同的监控数据差别很大，本文主要针对M ySQL和系统一共733个指标的监控数据。累计2 d按照固定时间间隔进行采样，获取733个时间序列，每个序列由2 056个数值组成，然后进行绘图和归类分析。M ySQL系统监控项非常多，这里只针对经常出现异常且较难定位的数据进行实验，实验所用的监控项如表1所示。

表1 实验监控项

通过对比观察，检测数据主要分为如图2～图4的情形。

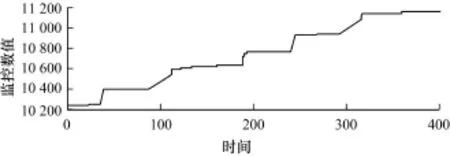
图2 M ySQL的com-begin监控项

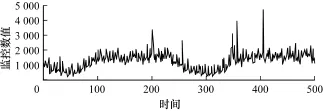
图3 M ySQL的com-change-db监控项

图4 M ySQL的created-tm p-tables监控项

对于图2和图4的情形，序列呈递增趋势。图2呈现阶段性抖动，图4较为平滑。要想体现数据的模式特征，图2需要的模式长度过长，因而导致模式数量过少，因此基于模式的异常检测无法适用。图3是符合此算法典型的数据模式，抖动频繁且平稳。图4数据呈现较为平稳的递增趋势，通过一次差分操作，便可去除均值变化对特征造成的影响，即可转化为类似于图3的数据。本文后续的分析主要针对图3类型的数据进行分析和实验。

2.2 基于模式的异常检测算法

由于监控数据剧烈的波动性，采用线性回归等方式对数据进行拟合分析效果不尽人意，因此对监控序列进行分段分析，每段作为一个模式，取模式特征进行描述，暂取均值和方差进行实验。这样将监控序列分为许多个模式，每个模式用一个特征向量来表示，将模式映射为二维空间上的一个点。由此可以引出模式距离等相关概念。

2.2.1 异常相关统计量

设时间序列为X=＜x1，x2，…，xn＞，通过线性分段方法得到的时间序列表示为：

L（X）=｛L（xi1，xi2），L（xi2，xi3），…，L（xi（n-1），xin）｝其中，L（xi1，xi2）表示连接两点的直线段。

模式：时间序列可以分为n个子序列，其中每个子序列称之为一个模式；模式取特征构成特征向量。

规范化处理：由于模式特征可能不在一个数量级，需要对各个特征值进行规范化处理，公式如下：

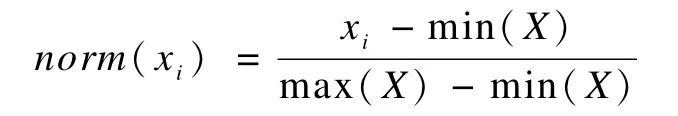
模式距离：使用规范化后的特征值向量的欧几里得距离表示为模式距离。

相关系数（k-count）：对每个模式计算其与其他模式的距离，取其中Top k个，然后将这k个模式的k-count计数自增一。认为当前模式可以到达这k个模式，实验中对k的取值进行多次调试，实验表明当其为模式数量的1/3时效果最佳。

影响因子：对k-count进行归一化处理：

异常因子：衡量模式的异常程度，n为某节点的k可达邻居的数量，则该点的异常因子为：

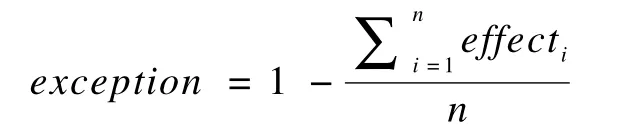
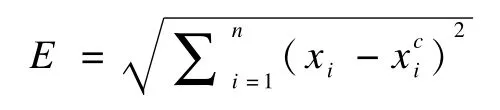
2.2.2 系统体系结构

系统以监控数据的时序序列作为输入，将模式映射到特征空间；然后计算各特征向量的距离，根据距离远近给出，根据设定的过滤条件给出异常区间和异常程度，系统架构如图5所示。

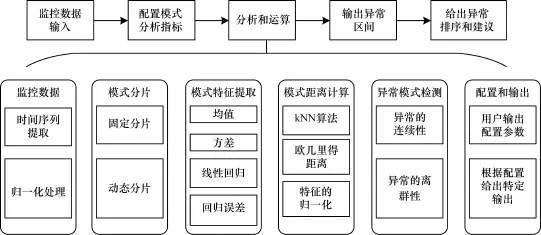
图5 异常检测系统架构

模式特征的选择和相关计算公式已经确定，模式的选择方式直接决定了最终结果的精确度。

2.2.3 各类模式选择算法

模式选择算法主要有以下3种：

（1）基于固定误差的模式选择算法

事先指定额定误差error和最小模式长度d，第1个模式从起点开始；依次向后拟合，若当前拟合的线段L（xi，xj）经过线性插值之后，和原来的数据拟合误差达到额定误差error之后，若j-i＞d，则将L（xi，xj）加入模式集合中；否则继续向后拟合到分段，到d为止；最终得到模式的集合。

基于固定误差的方法可以保证拟合误差，但是对于图2所示的数据不适用。剧烈的抖动会导致拟合片段过多；很难根据整体的数值特性判断额定误差的值，最小模式长度d也没有理论上的最优值。

（2）基于时态边缘算子的模式选择算法

文献［12］提出了基于时态边缘算子的异常检测算法。u表示时态边缘算子的检测窗口大小，d表示最短模式长度。利用时态边缘算子Teo（t，u）与时间序列X=＜x1，x2，…，xn＞做卷积运算，计算时间序列中各点的边缘幅度，交替取极大值和极小值点，将时间序列分割为各个不等长的子序列。

当设置了合适的u和d值时，效果优于固定长度分段和固定误差的方法。但是此算法也有必要的适用环境和前提：设置合适的u和d值；数据不可以类似图2剧烈抖动；对于线上的监控数据，这2个值很难直观确定，且大部分监控数据均为无规则抖动，因此不适合于监控数据分析。

（3）基于固定长度的模式选择算法

根据数据量和波动程度，设置模式长度，保证模式可以体现时序序列的特征；由于数据的剧烈抖动性，其他的拟合方式不是很适用。用户可以根据数据量的大小和数据的抖动特性，很容易地选择合适的模式长度。朴素的固定分段可以保证模式的代表性和模式的数量，取得更好的效果。

2.3 基于模式的异常检测算法

针对图2类似的数据，本文结合kNN聚类算法和基于模式的异常检测的思想，提出了基于模式的异常检测算法算法。实验表明，在数据规模达到一定程度时，可以很好地找到模式差异，定位异常区间。

算法首先将数据进行分段，每d个数据作为一个模式单元，计算每个模式的特征值，构成特征向量。再对每个模式计算求得距离最近的Top K个模式，将该模式加入到这K个模式的相关集合中，最后根据每个模式的相关模式的集合的大小以及和该模式相关的模式的影响因子计算该模式的异常程度。

算法 基于kNN和模式的异常检测算法

输入 时间序列X=＜x1，x2，…，xn＞，参数d，n，k

输出 异常区间（xi，xj），异常程度exceptioni

通过取特征，将各个分段映射为特征向量，并作归一化处理，可以有效提高算法对数据的适应性。各个特征向量之间的联系的紧密程度通过getdistance方法计算向量之间的欧几里得距离来衡量。

2.4 复杂度分析

上述算法获取Top K个邻居模式，可以采用基于快速排序的算法或者堆排序的算法，全部进行排序，算法复杂度为O（n×log（n）），但是由于只需要取前K个元素的排序，因此复杂度为O（n×log（k）），对每个模式如此操作，复杂度为O（n2×log（k））；其余操作均为O（n2）的复杂度；综上所述，算法复杂度为O（n2×log（k）），算法可以在多项式时间内完成计算，给出异常结果。

空间代价主要和模式数量有关，设有m个模式，每个模式需要存储与其他模式的距离，然后进行Top k运算。主要的内存消耗在模式中的距离列表，总体为O（m2）的空间复杂度。

3 实验结果与分析

针对上文提出的算法，基于M ySQL和系统的监控数据，与基于均值和方差的异常检测算法进行了对比实验，主要进行了环比分析和同比分析。环比分析指从一条监控序列看，某一时刻和其他大部分时刻相比，是否存在异常，用于发现趋势的异常；同比分析是将2天同一时刻的数据进行对比，比较监控数据的差异，消除人为因素的影响。

硬件环境：双核四线程i5-3210M CPU，频率为2.50 GHz，内存为DDR3 1 600 MHz双通道4 GB× 2。操作系统使用的是Ubuntu 12.04 64位desktop。软件环境：程序基于Java编写，IDE为Eclipse Kepler，JDK版本为1.6。数据环境：M ySQL服务器连续两天的监控数据，每个监控项采集2 056个数据项，构成733个时间序列。模式长度d设置为50，报警阈值k设置为0，连续n报警设置为1。这样会输出所有的模式的异常程度。系统针对应用需求，实现了环比分析和同比分析2种功能，并且针对3种模式选择方式进行了对比实验。

3.1 应用场景分析

本文系统主要针对大规模的监控数据，运维人员难以定位数据异常所在的情况下，通过环比和同比分析，给出异常区间，方便对问题的快速定位。

3.1.1 环比分析

当监测数据量过大，运维人员不得不查看很长的时间序列，这就对系统提出了环比分析的需求。环比分析根据监控数据的趋势进行统计分析，找到和绝大多数区间不同的区间，定位问题发生的时间段。采用M ySQL的bytes-received-pt监控项2天的数据进行实验，此监控项可以很大程度反映用户的访问量的变化，如图6所示。

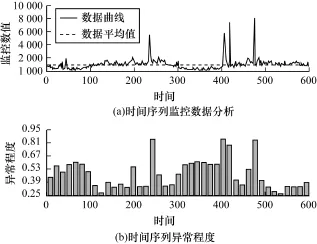
图6 监控数据的环比统计分析

从图6明显可以看出，对应的区间异常程度明显高于其他区间，效果较为明显。

3.1.2 同比分析

由于用户行为不同时段的差异造成监控数据不同时段差异很大，因此对系统提出了同比分析的需求，对照2天的监控数据，定位异常区间。依然选择bytes-received-pt监控项2天的数据进行同比分析。

图7（a）、图7（b）中的曲线均为2天的系统监控数据的时序序列，按照时间进行对齐。图7（c）表示其异常程度。

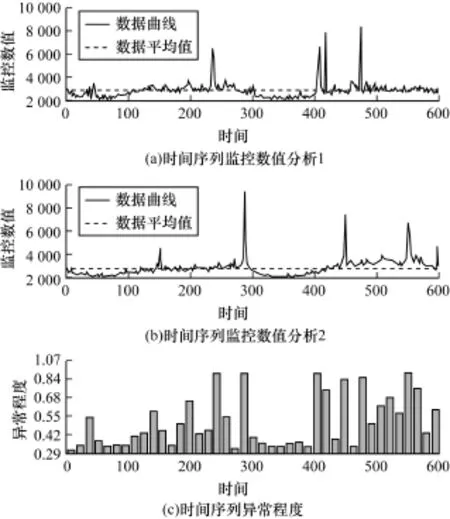
图7 监控数据的同比分析

可见，若2条曲线差异性决定了柱状图的高低，同比分析在此数据上可以取得较好的准确性。

3.2 实验对比

针对此类监控数据，传统的异常检测算法通常采用均值加上k倍标准差设定阈值，根据阈值的偏离程度计算异常程度，进而决定是否报警。由于均值和方法常常不在一个数量级，因此通常也需要先对数据进行归一化处理，然后再计算均值和方差，给出阈值。

这类算法的适用性有限，而且需要根据不同的数据调整k值。本文提出的算法通过基于模式的异常检测算法，结合kNN思想，对数据进行了抽象化处理，减少了对数据的依赖，具有更好的适用性，并且效果明显。

将算法1与基于均值和方差的异常检测算法进行实验对比，验证方法的有效性。固定长度分段，模式长度d为50个、2 056个数据组成时间序列，构成41个模式。数据曲线和异常柱状图如图8所示。

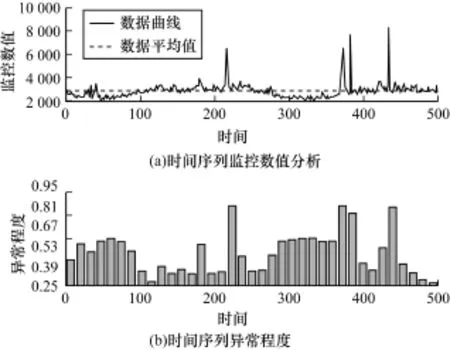
图8 基于模式和kNN算法的数据分析

后面针对同样的数据，采用传统的均值加上k倍标准差的方法进行异常检测，根据此数据对k进行调整和尝试，效果如图9所示。

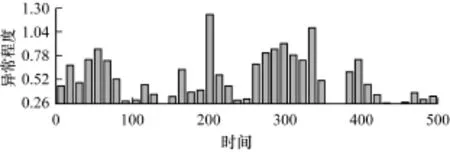
图9 朴素异常检测算法（k=0.1）结果

如图10所示，k的选择直接决定了阈值区间的大小，也决定了结果的精确度。但k不是可以直接根据数据趋势进行经验选择的值，需要经过统计分析才能得到最优值；本文算法只需要模式长度一个参数即可，根据曲线图即可直观地选择合适的数值，保证具有一定的代表性即可，具有更好的可用性。

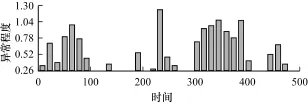
图10 朴素异常检测算法（k=0.3）结果

从图9和图10的对比可以明显看出，朴素的异常检测算法，即使给定优化后的k，异常程度的显著性和异常区间的范围不够精确，相对而言，本文提出的算法精度提高约50%。

4 结束语

本文根据监控统计数据的特点，针对其剧烈抖动的特性，结合基于模式的异常检测算法和kNN思想，提出了一种新的异常检测算法。相较于以往的基于均值和方差的异常检测算法，本文算法在可用性和精确度方面有了一定的提升。后续工作主要包括以下2个方面：（1）本文系统暂时采用均值和方差作为特征值，可以根据不同的数据特征选择不同的特征值，提高精度；（2）模式长度目前是固定的，可以考虑根据数据特性自动进行模式长度的调优，提高系统的适用性和计算结果的精度。

［1］ Hodge V J，Austin J.A Survey of Outlier Detection Methodologies［J］.Artificial Intelligence Review，2004，22（2）：85-126.

［2］ 李光强，郑茂仪，邓 敏.时空数据异常探测方法［J］.计算机工程，2010，36（5）：35-36，39.

［3］ Rousseeuw P J，Hubert M.Robust Statistics for Outlier Detection［J］.Wiley Interdisciplinary Review s：Data Mining and Know ledge Discovery，2011，1（1）：73-79.

［4］ Jiang M F，Tseng S S，Su C M.Two-phase Clustering Process for Outliers Detection［J］.Pattern Recognition Letters，2001，22（6）：691-700.

［5］ He Z，Xu X，Deng S.Discovering Cluster-based Local Outliers［J］.Pattern Recognition Letters，2003，24（9）：1641-1650.

［6］ Esling P，Agon C.Tim e-seriesData Mining［J］.ACM Computing Surveys，2012，45（1）：12-19.

［7］ Breunig M M，Kriegel H P，Ng R T，et al.LOF：Identifying Density-based Local Outliers［J］.ACM Sigmod Record，2000，29（2）：93-104.

［8］ 陈 乾，胡谷雨，路 威.基于距离和DF-RLS的时间序列异常检测［J］.计算机工程，2012，38（12）：32-35.

［9］ Jin W，Tung A K H，Han J.Mining Top-n Local Outliers in Large Databases［C］//Proceedings of the 7th ACM SIGKDD International Conference on Know ledge Discovery and Data Mining.New York，USA：ACM Press，2001：293-298.

［10］ Papadim itriou S，Kitagawa H，Gibbons P B，et al.LOCI：Fast Outlier Detection Using the Local Correlation Integral［C］//Proceedings of the 19 th International Conference on Data Engineering.Washington D.C.，USA：IEEE Press，2003：315-326.

［11］ Yoon K A，Kwon O S，Bae D H.An Approach to Outlier Detection of Software Measurement Data Using the K-means Clustering Method［C］//Proceedings of the 1st International Symposium on Empirical Software Engineering and Measurement.Washington D.C.，USA：IEEE Press，2007：443-445.

［12］ 肖 辉，马海兵，龚 薇.基于时态边缘算子的时间序列分段线性表示［J］.计算机工程与应用，2008，44（19）：156-159.

编辑索书志

MySQL Outlier Detection Algorithm Based on Monitoring Data

LING Jun1，2，Y IN Boxue2，LISheng2，WANG X in1
（1.School of Computing Science and Technology，Tianjin University，Tianjin 300072，China；2.Baidu（China）Co.，Ltd.，Beijing 100085，China）

With the explosive grow th of the data on the Internet，the scale of the server cluster is rapidly expanding. How to carry out large-scale cluster monitoring and analysis becomes a difficult problem in the Internet industry. Therefore，this paper presents a new method for detection and analysis of the monitoring data according to the monitoring jittering data.It adopts pattern-based outlier detection method without setting a threshold，takes the eigenvalues，calculaties the outliers，and obtains the abnormal range and degrees.Experimental results show that the algorithm can extract data features for time sequence of jittering data，and has a higher precision and better applicability than the outlier detection algorithm based on mean-variance.

outlier detection；monitoring data；statistics；pattern；time sequence

凌 骏，尹博学，李 晟，等.基于监控数据的MySQL异常检测算法［J］.计算机工程，2015，41（11）：41-46.

英文引用格式：Ling Jun，Yin Boxue，Li Sheng，et al.MySQL Outlier Detection Algorithm Based on Monitoring Data［J］. Computer Engineering，2015，41（11）：41-46.

1000-3428（2015）11-0041-06

A

TP393

10.3969/j.issn.1000-3428.2015.11.008

第三届“百度主题研究”基金资助项目。

凌 骏（1991-），男，硕士研究生，主研方向：RDF图数据管理，M ySQL数据库技术；尹博学、李 晟，硕士；王 鑫，副教授、博士。

2014-11-03

2014-12-02 E-m ail：lingjun@tju.edu.cn