贝叶斯线性分层模型估计个体农业保费

王晓园，蒋经农

(遵义医学院医学信息工程系，贵州遵义 563003)

近年来农业保险越来越受到人们的关注。农业经营者投保农业保险最大益处是在任何情况下都能保证农业生产的收支平衡［1］。其主要是根据农作物单位面积产量，把农业生产中不可预期损失转化为较低水平的保费［2］。农业生产风险主要是因恶劣天气、病虫害等相关不利因素影响而造成的经济损失。农业保险发展缓慢最主要的原因是缺乏相关长期统计数据和精确估计公平保费的模型与方法。通常保险公司收到的总保费少于总赔偿金，这将造成保险公司巨大的经济损失，因此保险公司承保农业保险存在巨大风险。通常在发达国家这部分损失由政府补偿，这是许多国家农业保险发展缓慢，甚至许多保险公司不愿承保农业保险最主要的原因［3］。

基于农作物产量受空间时间分布影响的特点，采用分层贝叶斯方法［4－5］构造空间时间线性分层混合相依模型。分层模型拥有分析纵向数据的自然优势，其核心是在模型中引入随机效应来体现“目标”组内数据的相关性和不同“目标”组间的异质性。可以把农作物产量数据视为分层数据，利用分层模型进行分析，这样不但体现了同一年内农作物单位面积产量数据的纵向特征，以反映组内数据的相关性，也考虑了不同年份由未观测到的特征所引起的异质性，能更准确预测期末农作物单位面积产量，为更精确估计公平合理的个体农业保费提供依据。

1 补偿金模型

假设农业经营者在保险期末单位面积的实际产量低于单位面积的承保产量时就会获得补偿金。这种农业保险被称为个体农业保险，表达式如下［6］:

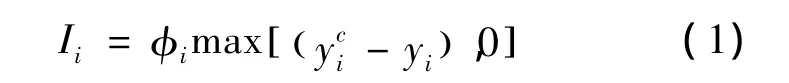
式中:φi是一个可调节系数(0＜φi＜1);yci表示承保产量;yi表示实际产量。在农业保险合同中农业经营者可以自主选择一个承保等级αi(0≤αi≤1)。单位面积的承保产量表示第i个生产区域农作物单位面积产量的期望值。

2 分层线性混合相依模型构造

研究大量不同区域农作物单位面积产量的统计数据，可知其呈现以下特点:趋向性;自回归效应［7］;异方差性［8］。单位面积产量统计数据的异方差性呈现地域性特点，如平原地区农业机械化程度相对较高，发达地区农业生产新技术、新设施设备应用较广;同时存在广泛相依性，如某区域内某种农作物发生某种病虫害，邻近区域会受到一定程度影响，这种相依性为构建空间时间相依模型奠定了基础。

通常，农作物产量统计数据的趋向性由空间时间混合模型模拟［9－10］，时间参数 T通常被中心化以提高 MCMC 算法［11－12］的收敛速度，T*=而不同区域间基础设施水平差异和新科学技术推广程度以及一些更合理、有效的新方法应用使得不同区域单位面积产量数据呈现异方差性，这种异方差性主要由空间异方差参数vi模拟，vi服从Gamma分布。

3种分层线性模型(hierarchical linear models，HLM)［13－14］构造如下:

1)含随机截距项的一元正态HLM。

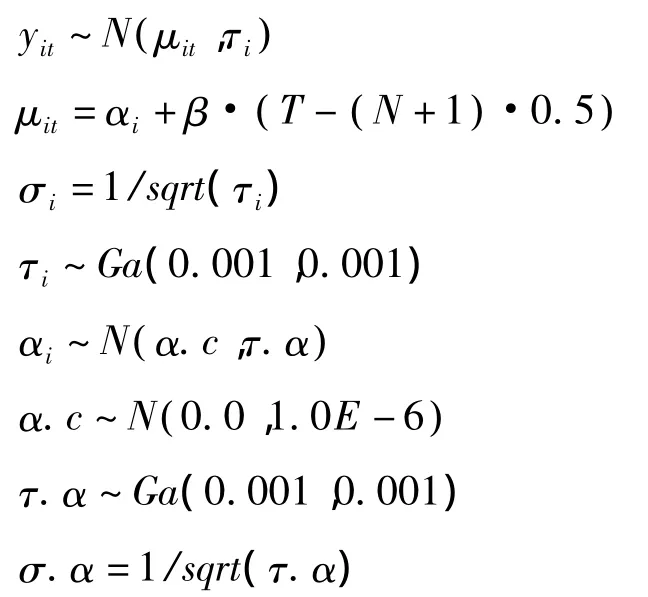
2)含随机截距、随机斜率项的一元正态HLM

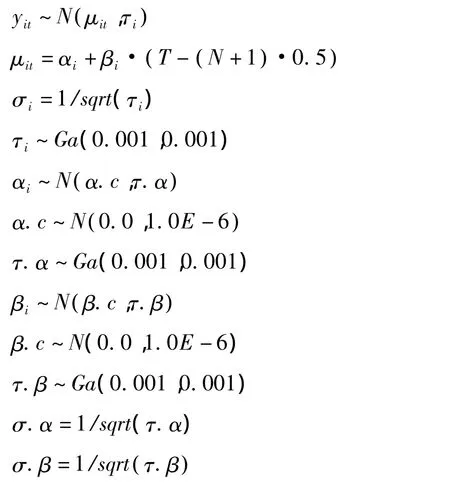
其中mean［］，prec［，］为常量。

3 实例分析

对3个模型实例(表1～4)模拟结果(图1～3)比较分析得出以下结论:模型1估计各量的均值较小，方差较大，估计结果较粗略;模型2估计各量的均值相对较大，方差较小，估计结果较稳定;模型3估计各量的均值相对较大，和模型2估计各量的均值相比相差不大，但模型3估计各量的方差比模型2估计各量的方差稍小，估计结果较准确。据此可利用模型3的估计结果做进一步分析。

保险公司依据Y的后验预测描述性统计量，由纯保费计算原理(即期末损失的均值为零)，通过式(1)可估计出φi的精确值。

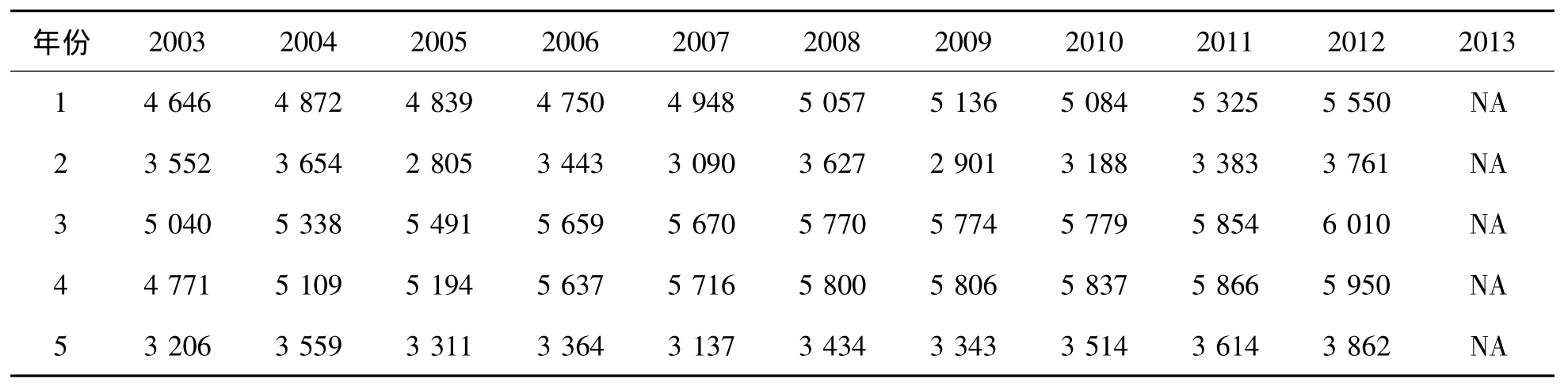
表1 5个不同省份各年单位面积谷物的产量 kg/hm2

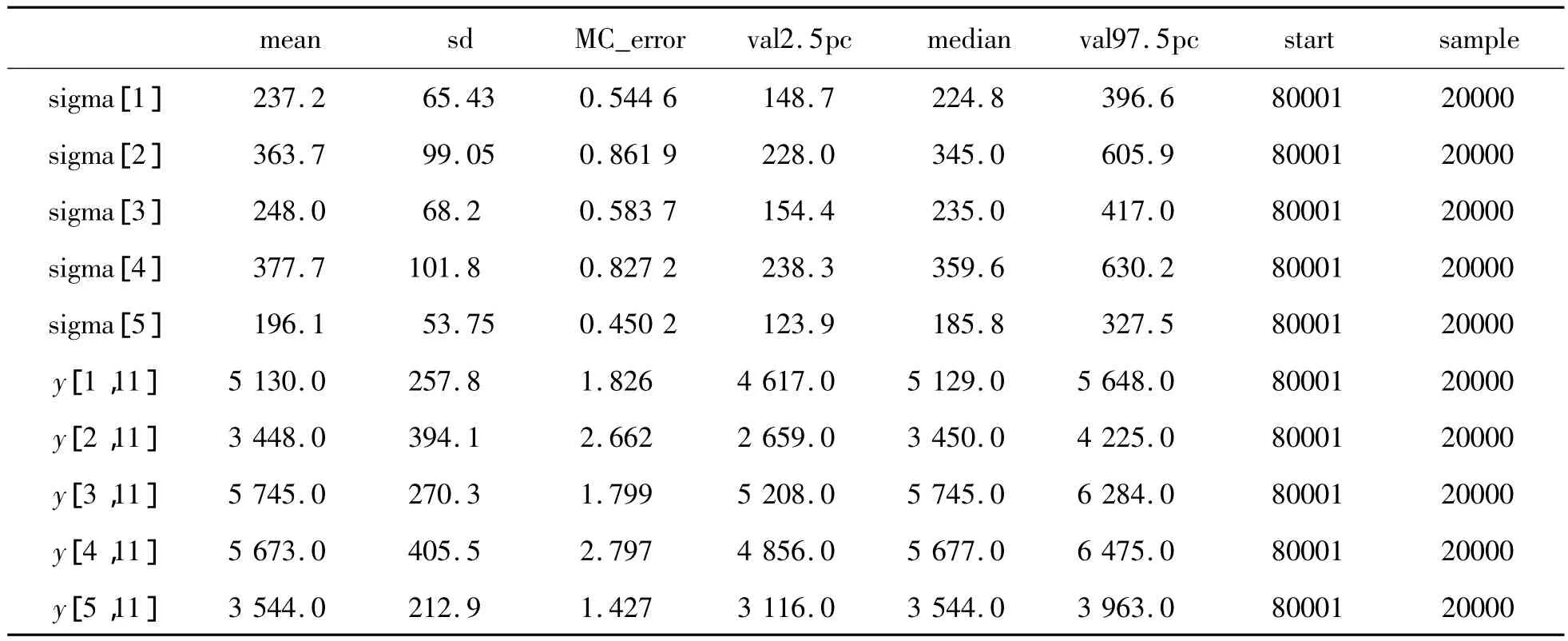
表2 模型1对2013年各省单位面积谷物的预期产量(kg/hm2)及sigma的估计

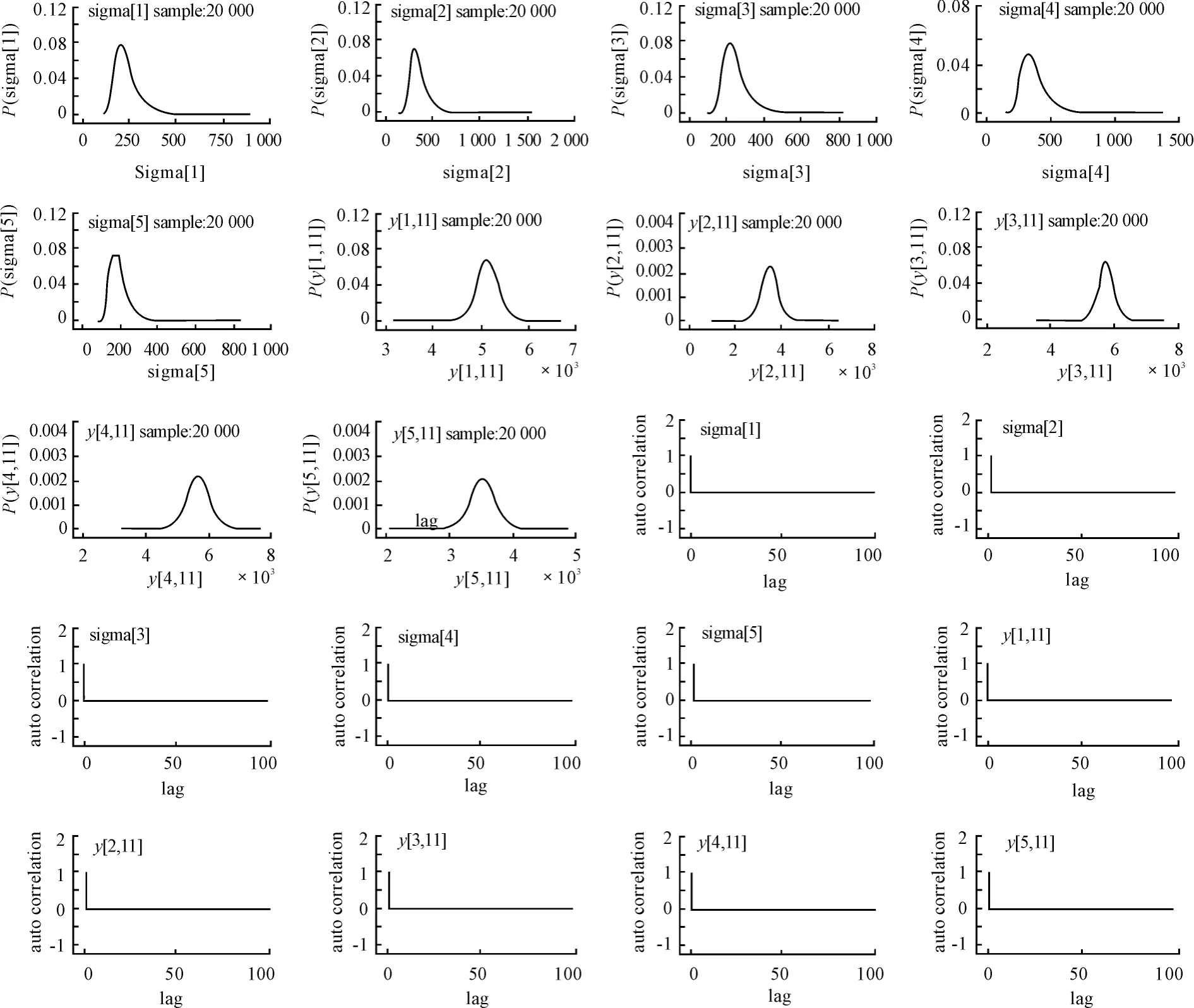
图1 模型1中2013年各省单位面积谷物的预期产量及sigma的核密度和自相关函数

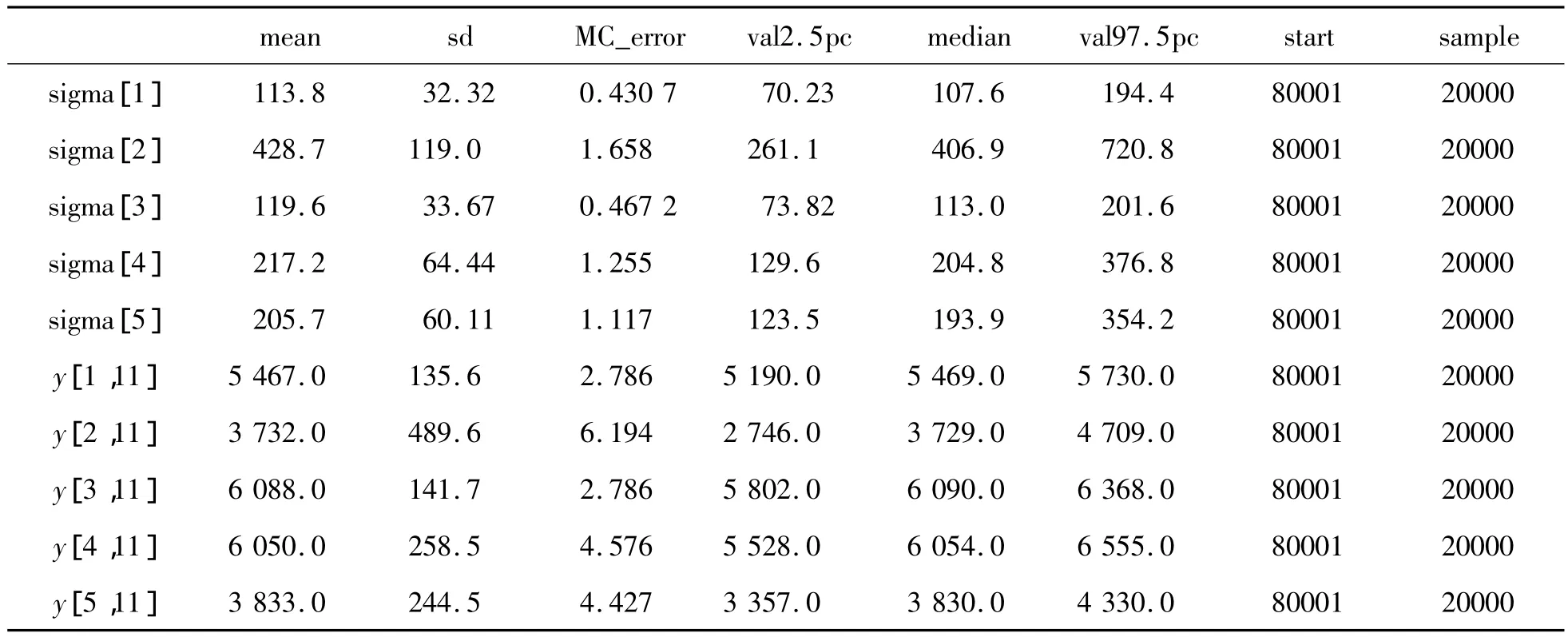
表3 模型2对2013年各省单位面积谷物的预期产量(kg/hm2)及sigma的估计

图2 模型2中2013年各省单位面积谷物的预期产量及sigma的核密度和自相关函数

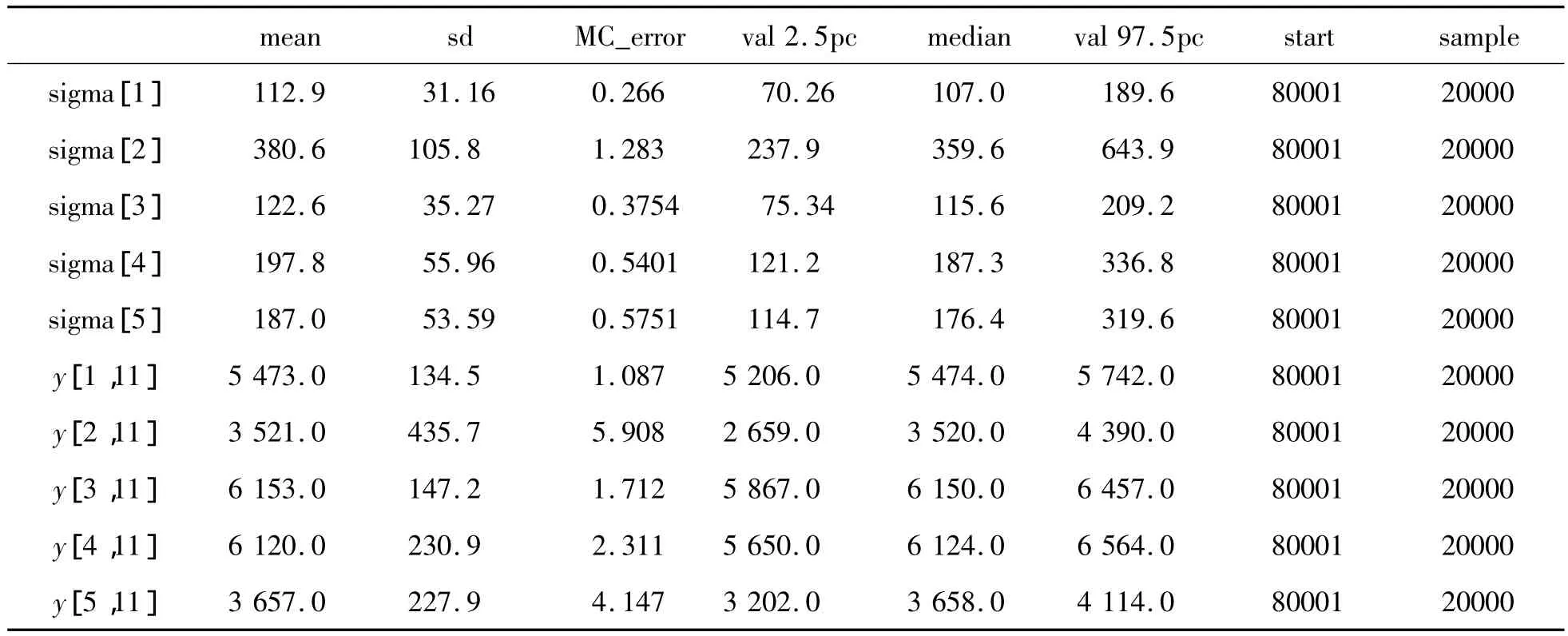
表4 模型3对2013年各省单位面积谷物的预期产量(kg/hm2)及sigma的估计

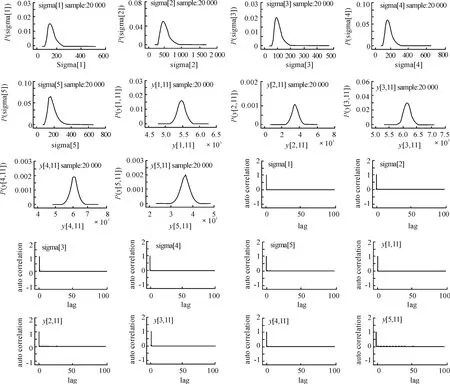
图3 模型3中2013年各省单位面积谷物的预期产量及sigma的核密度和自相关函数

4 结束语

本文基于农作物单位面积产量数据的纵向特征，考虑数据序列内的相依性构造了预测单位面积产量的时间空间相依模型，其中单位面积产量的均值由空间时间混合相依模型模拟。同时考虑不同区域农作物单位面积产量的差异性，即考虑受空间分量对方差的影响，没有考虑单位面积产量随时间变化引起的异方差性(通常在短期内这种差异较小)，但考虑到估计的精确性仍需对异方差性做进一步研究。同时，还可以利用其他一些与农业生产相关的信息(如地理信息、气象信息、病虫害历史数据等)建立更完善的农业保险模型。此外还需进一步研究与农作物单位面积产量相关统计量的分布类型，以提高预测的精确性。

［1］Makov U E.Principal Applications of Bayesian Methods in Acturaial Science:A Perspective，(with discussion)［J］.North American Actuarial Journal，2001，5(4):53－73.

［2］吴岚.风险理论［M］.北京:中国财政经济出版社，2006:29－30.

［3］Ruiz-Cardenas R，Ozaki V A.A Proposal to Pricing Area Yield Crop Insurance Contracts Using Spatio-Temporal Bayesian Dynamic Models［J］.Empir Econ ，2009，34:1－4.

［4］Gómez-Déniz E ，Vázquez-Polo J F J，Pérez M.A Note on Computing Bonus-Malus InsurancePremiums Using a Hierarchical Bayesian Framework［J］.Sociedad de Estadística e Investigación Operativa Test，2006，15(2):345－359.

［5］吴永，王晓园.贝叶斯方法估计极端损失再保险纯保费［J］.重庆理工大学学报:自然科学版，2011(4):106－111.

［6］Paramjit S G.Bayesian Analysis of Dyadic Data［J］.NORTH AMERICAN ACTUARIAL JOURNAL，2005，17:1－24.

［7］师义民.数理统计［M］.3版.北京，科学出版社，2009:190－214.

［8］Vitor A O.princing farmer-lever agricultural insurance a Bayesian approach［J］.Empir Econ，2009，36:231－242.

［9］傅军.基于先验信息的贝叶斯统计检验和经典统计检验的比较［J］.统计决策，2008(2):155－156.

［10］Pinheiro J C，Bates D C.Mixed-effects models in s and splus［M］.New York:Springer-Verlag，2000.

［11］David P M.Actuarial Modeling with MCMC and BUGS［J］.North American Actuarial Journal，2000，22:96－125.

［12］Yong Wu，Xiaoyuan Wang，Na Liu.Monte Carlo method with application in Automobile Insurance［EB/OL］.［2005－05－05］.http:E-Business and Government(ICEE)2011 Internation Conference.

［13］Raudenbush S W.Hierarchical linear models applications and data analysis method［M］.SAGE Publications:Second Edition，2002.

［14］Gelman A.Data analysis using regression and multilevel/hierarchical models［M］.New York:Cambrige University Press，2007.