基于Fisher模型的NBA季后赛资格预测

高红霞，杨 迪，苏理云，黄丹妮

(重庆理工大学数学与统计学院，重庆 400054)

在NBA获得总冠军不仅是至高无上的荣誉，更能为球队带来不菲的经济效益。然而，季后赛是所有向往总冠军球队必须迈过的一道坎。因此，一个球队能否进入季后赛至关重要，利用已知数据对球队能否进入季后赛进行判断变得具有实际意义。李杰林等［1］利用Logistic模型对季后成绩进行研究。潘建武［2］采用Fisher判别分析对常规赛胜负进行判别，而国内对NBA球队能否进入季后赛的预测模型则较少。本文利用2011—2013两年季的数据作为样本，采用Fisher法建立判别模型，预测2014年季后赛资格，发现预测的误判率较小。最后，本文基于2012—2014两年的数据重新建立模型，对已经过去1/3赛程的2014—2015季后赛资格进行判别。

1 指标与数据

1.1 指标的选取

本文参考李杰林［1］和潘建武［2］对 NBA 球赛胜负的分析，选择2分命中率、3分命中率、罚球命中率、防守篮板、进攻篮板、助攻数、抢断、阻挡、转换得分、个人犯规，场均得分等指标。考虑到影响篮球比赛胜负的两大因素是对手和自己，仅选取自己的指标预测胜负具有片面性。比如一些进攻比较好的球队虽然可能得到很漂亮的数据，但因为防守漏洞导致对手得到更多分数而输掉比赛，所以本文参考薛薇［3］在Logistic回归模型中定义的优势比，根据式(1)定义所选指标的优势。

将所有指标及其优势的符号整理成表1。

1.2 数据的收集

本文从 NBA官方网站［4］上获取2011—2014赛季常规赛的数据和2014—2015赛季1/3赛程的数据。其中，Ti是自己球队每个指标的平均;Oi是对手每个指标的平均;Ωi是每个指标的优势比。

表1 选取指标的符号及含义

2 Fisher判别法原理

2.1 基于Fisher判别法的NBA季后赛预测模型

Fisher判别法也称典型判别法［5］，其基本思想是先将高维空间数据投影到低维空间，然后再进行判别。

对于本文来说，数据的维度即是选取指标的个数。所谓投影，即是将p=11维空间的样本点投影到m(m＜p)空间中。Fisher判别函数是各指标优势的线性函数，即

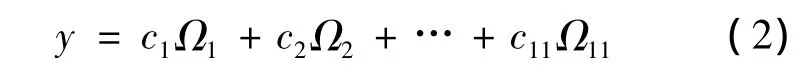
首先，应在判别变量的p维空间中找到使各类别的平均值差异最大的线性组合作为第1维度，代表判别变量组间方差最大的一部分，得到第一Fisher判别函数。

然后，依次找到第二Fisher判别函数、第三Fisher判别函数等，且判别函数之间独立。

2.2 Fisher判别模型的求解

从 k 个总体 Gt(t=1，2，3…k)，分别从 Gt抽取nt个p维样本，有

将Ω(t)i数据投影到p维常数向量C上，得到投影点的一元线性组合:

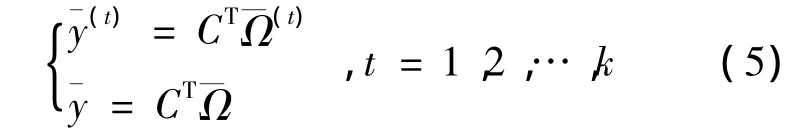
E和B分别具有自由度n－k和k－1，则一元方差分析统计量为:

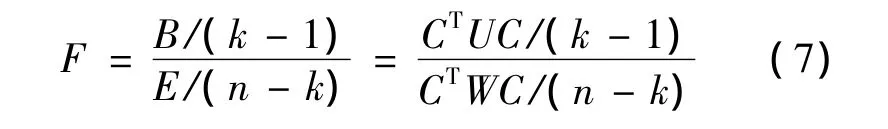
式(7)中的F值越大，表明总体样本Gt之间的均值有显著性差异;F值越大，也使得对系数C的目标函数值Φ(C)达到极大值。

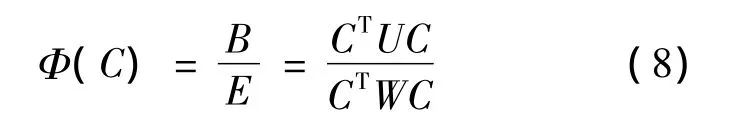
由特征值极值性质可知，式(8)中求Φ(C)的极大值问题可转化为求W－1U的最大特征值和特征向量问题，其极大值求解方程如下:

式(9)中的最大特征根则为W－1U的非零特征根，即 λ1≥λ2≥…λr(r≤p)。

根据λ1≥λ2≥…λr(r≤p)对应的特征值依次得到第一判别式。

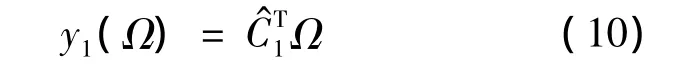
式(10)中 i=1，2，…，r。

2.3 Fisher判别规则的建立

本文将所有球队分为季后赛球队和非季后赛球队，即为两总体的样本，Fisher判别规则如下:

其中

若y＞y0，即判别为季后赛;反之，则判为非季后赛。

2.4 模型判别能力的评价

一个判别模型判别能力的高低表现为误判率的高低。本文采取留一交叉验证法来衡量模型的判别能力［6－7］。所谓交叉验证法，是从样本中抽取1个样本作为验证样本，其余的样本作为训练样本。它既避免了样本数据在构造判别函数的同时又被用来对该函数进行评价，造成不合理的信息重复使用，又几乎避免了构造判别函数时样本信息的损失(只损1个样本)。

3 实证分析

3.1 基于优势得分和原始指标的模型效果对比

本文根据以上对Fisher判别模型的求解思路，在 R 中编程［8－10］。对 2011—2012 和 2012—2013 NBA赛季的数据建立Fisher判别模型，求得交叉误判率。基于原始指标的判别信息如表2所示。

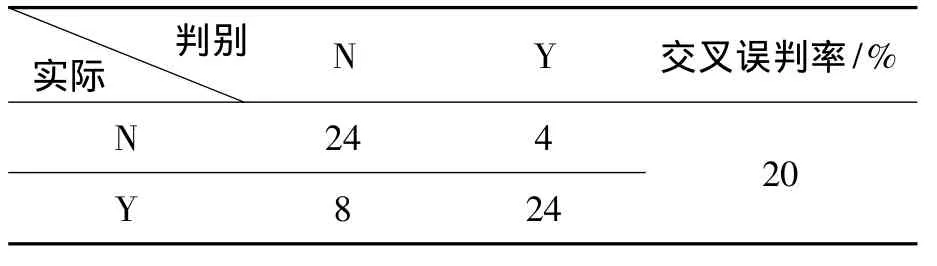
表2 基于原始指标的Fisher判别信息

表2中的交叉验证的误判率为20%，可以看出判别效果不是太好。

篮球竞技的胜负因素，取决于自己和竞争对手。在篮球比赛中能限制对手优势、发挥自己优势方能取得胜利。因此，本文选择用每个指标的优势得分作为新的判别指标进行判别分析，判别结果如表3所示。

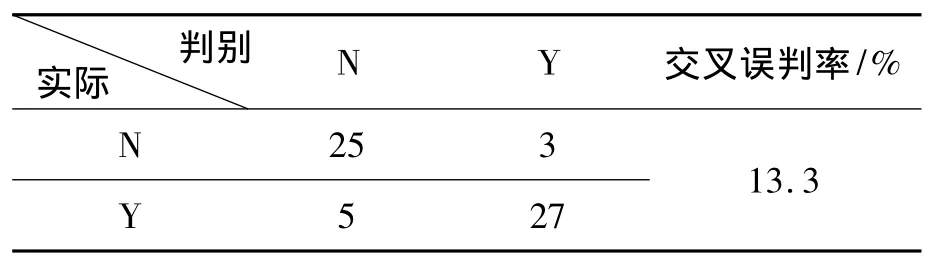
表3 基于优势得分的Fisher判别信息

从表3可以看出:采用优势得分作为新的指标进行判别分析，交叉误判率降为13.3%。

3.2 对Fisher判别模型的进一步修改

本文将对误判断样本以求能够进一步降低误判率，误判样本如表4所示。

从表4可以看出:在5支被误判为非季后赛的球队中，其中有3支是东部球队;在3支被误判为季后赛的球队中有2支是西部球队。究其原因，纵观近年来NBA格局，西强东弱的格局越来越清晰，一些东部的季后赛球队放在西部却无法进入季后赛，一些在西部不能进入季后赛的球队，放在东部却可以进入季后赛。鉴于以上原因，分别对东、西部建立Fisher判别模型。

表4 误判样本信息表

对东、西部分别建立Fisher判别模型，采用交叉验证法检验模型的判别能力，将判别信息整理，结果如表5所示。

表5 东西部球队误判样本信息

从表5可以看出:分东、西部建立Fisher判别模型后，西部的交叉误判率没有降低，但东部的交叉误判率降为10%，平均交叉误判率降为11.65%，故分东、西部建立的判别模型能得到较优的结果。

3.3 基于本文的判别模型对2013—2014赛季预测

在进行Fisher判别分类时，2个总体的个数是未知的，但由于获得季后赛资格的名额有限，每个赛区只有一个，所以本文选取Fisher函数值较大的前8个队作为组2(季后赛组)，其余为组1(非季后赛组)。根据以上规则，利用Fisher判别函数(11)和(12)进行预测分类，并对比2013—2014赛季实际季后赛情况，结果见表6。

表6 Fisher判别信息和真实信息

由表6可知:西部只有1支没有进入季后赛，即认为误判率为12.5%;而东部预测的8支季后赛球队都进入季后赛，即误判率为0%。由此可以看出:Fisher判别模型具有较好的预测能力，能够较精确地预测出16支季后赛球队。

3.4 基于2012—2014赛季的数据对2015赛季的预测

在本文 3.3节中发现基于 2012—2013和2013—2013赛季数据建立的模型能够较好地预测2013—2014赛季季后赛资格，所以本文考虑采用近2个赛季(即2012—2013和2013—2014赛季)的数据作为训练样本对已经进行了1/3的2014—2015赛季季后赛资格进行预测，预测结果见表7。

表7 2014—2015赛季30支球队的预测结果

从表7可以看出:传统强队诸如马刺、公牛等队都在预测的季后赛行列中。

4 结束语

作为世界三大主流球类之一，篮球市场越来越火爆。一支球队能否在季后赛的大舞台上表演，直接与球队的经济利益相关联，因而对球队能否进入季后赛的预测显得十分有意义。基于2011—2012和2012—2013赛季数据建立 Fisher判别模型来判别一支球队能否进入季后赛，发现东、西部存在明显差异;进而分东、西部建立另一个Fisher判别模型，回代误判率仅为5%;然后对2013—2014赛季季后赛资格预测。对比已知信息，发现西部的8支球队中只有1支误判，预测误判率为12.5%;东部的8支球队全部预测准确，预测误判率为0%，说明模型具有较好的预测效果。最后，本文基于2012—2013和2013—2014赛季的数据重新建立东、西部的判别模型，并根据已经进行了1/3的2014—2015赛季的数据预测了今年的16支季后赛球队。

［1］李林杰，张学东.影响NBA常规赛胜负的Logistic分析［J］.统计教育，2008(4):40－41.

［2］潘建武.对NBA常规赛胜负影响因素及Fisher判别分析［J］.四川体育科学，2012(5):47－48.

［3］薛薇.基于R的统计分析与数据挖掘［M］.北京:中国人民大学出版社，2014.

［4］Sports Reference LLC［DB/OL］.［2014－12－31］.http://www.basketball-reference.com/seaons/.

［5］高慧璇.应用多元统计分析［M］.北京:北京大学出版社，2005.

［6］赵萌，兰德新.基于多元统计分析的大学生消费调查［J］.重庆理工大学学报:自然科学版，2012，26(7):123－126.

［7］魏伟，颜醒华.基于多元回归分析的中国旅游上市公司投资效率研究［J］.重庆师范大学学报:自然科学版，2013(5):128－133.

［8］王斌会.多元统计分析及R语言建模［M］.广州:暨南大学出版社，2014.

［9］汤银才.R语言与统计分析［M］.北京:高等教育出版社，2008.

［10］薛薇.基于R的统计分析与数据挖掘［M］.北京:中国人民大学出版社，2014.