基于RSSI和融合智能优化算法的无线传感器网络定位算法

张先超，刘兴长，钟一洋，张春园

(后勤工程学院 a.后勤信息与军事物流工程系;b.学员旅，重庆 401311)

无线传感器网络(wireless sensor networks，WSN)是由随机部署在目标区域内的数量巨大的离散传感器节点组成，通过无线通信方式形成的一个多跳的自组织网络系统［1］。节点的位置信息至关重要，在导航、跟踪、监控等应用中起关键性作用。根据是否需要测量节点间的距离，定位可以分为基于测距(range-based)的定位和无需测距(range-free)的定位;根据部署的场合可分为室外定位和室内定位［2］。通常情况下，基于测距的定位算法的定位精度高于无需测距的定位算法的定位精度。基于测距定位的常用方法包括角度定位(AOA)［3］、三边定位(trilateration)和极大似然估计等。常用的测距方式包括接收信号指示强度(RSSI)［4］、信号传播时间/时间差/往返时间(TOA/TDOA/RTOF)［5］、接收信号相位差(PDOA)、近场电磁测距(NFER)等。由于基于RSSI的测距方式无需增加额外设备、简单易行，在近年来发表的研究成果中得到广泛采用。

近年来，许多学者将智能算法应用于基于测距的无线传感器网络定位算法中。文献［6－7］使用粒子群优化算法定位，取得了优于极大似然估计法等算法的定位结果，但是由于单一智能算法性能存在缺陷，必须进行改进以满足无线传感器网络定位的实际应用。文献［8－10］针对粒子群优化算法的缺点提出改进算法，克服了粒子群优化算法后期易陷入局部最优的缺陷，进一步提高了定位精度。但是上述改进算法避免粒子陷入局部最优的能力有限，不能保证粒子有效逃离局部最优。针对基于粒子群优化的无线传感器网络定位算法后期易陷入局部最优、算法稳定性较差的缺陷，提出一种粒子群和人工鱼群融合优化算法，将其应用于无线传感器网络节点定位中，以克服上述缺陷，提高定位算法的性能。

1 RSSI测距模型

节点在通信时可以直接获取RSSI值，估计出未知节点与锚节点的距离。很多学者对RSSI测距进行了深入研究，根据实验环境的不同建立了多种基于RSSI的测距模型。其中，对数－常态分布模型(log-distance distribution)考虑了实际环境的复杂性，能反映信号传播过程中引入的噪声对测距结果的影响［11－12］。对数－常态分布模型路径损耗计算公式如下:

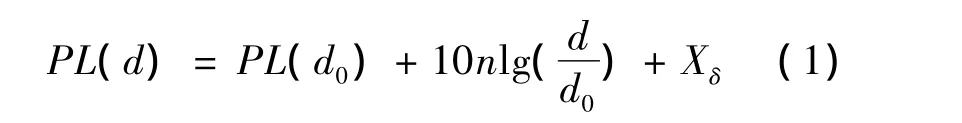
式(1)中:d为发射端与接收端之间的距离;PL(d)是经过距离d后的路径损耗;n为信道衰减指数，一般取值为2～5;Xδ是均值为0、标准差为δ的高斯随机噪声变量，标准差的取值一般为4～10;d0是参考距离，一般取1 m。对式(1)化简得到:

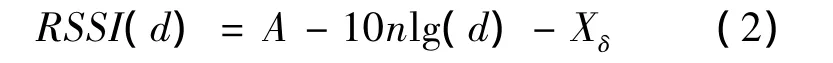
式(2)中A为1 m处的RSSI值。通常情况下，测距误差随着测量距离的增加而增大［13］，即由较大的RSSI值计算得到的距离值误差较小，而由较小的RSSI值计算得到的距离值误差较大。

2 相关知识

2.1 粒子群优化算法

粒子群优化(particle swarm optimization，PSO)算法是在无线传感器网络定位中常用的一种群体智能优化算法，文献［6－10］均采用PSO算法或改进的PSO算法。PSO算法是一种操作简单的群体智能优化算法，其实现原理如下:

假设在D维的搜索空间内，存在一个种群大小为M的粒子群;存在一个数量为N的搜索目标群。每个粒子在空间中的位置坐标 xi=(xi1，xi2，…，xid)，搜索速度 vi=(vi1，vi2，…，vid)，搜索到的个体最优位置为pi=(pi1，pi2，…，pid)，搜索到的全局最优位置为gb=(gb1，gb2，…，gbd)，其中，i=(1，2，…，M)，d=(1，2，…，D)。算法采用下列公式对粒子进行操作［14］:

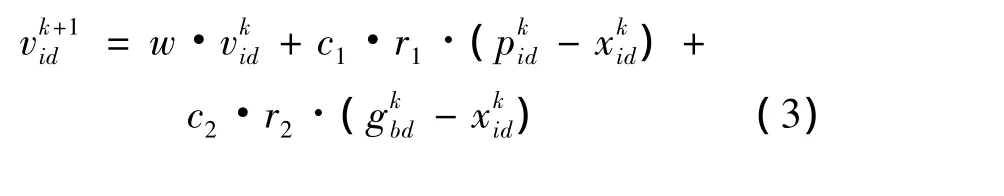
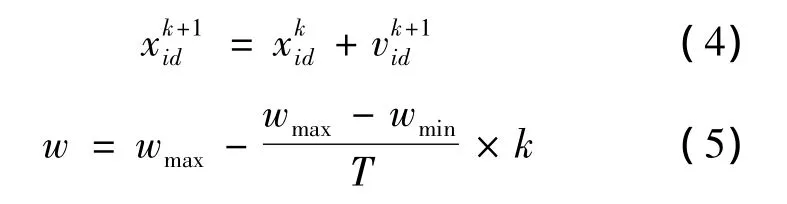
式中:学习因子c1和c2是非负的常数，常设c1=c2=2;r1和r2是介于［0，1］的随机数;w为惯性权重，用来保持局部搜索和全局搜索的平衡，较大的w有利于算法的全局搜索能力，较小的w有利于算法的局部搜索能力;vid∈［－vmax，vmax］，vmax过大容易使粒子飞离最优解，vmax过小容易使粒子陷入局部最优，粒子的速度通常设为每维变换范围的10%～20%;k为当前迭代次数;T为终止迭代次数。

2.2 人工鱼群算法

人工鱼群(artificial fish school，AFS)算法由李晓磊等于2002年提出［15］，是一种全局寻优能力强、简单、易操作的群体智能优化算法。该算法通过模拟鱼类的觅食、群聚、追尾、随机等行为在搜索域中进行寻优。AFS算法的数学模型中各变量参数描述如下:人工鱼群个体大小为N;人工鱼个体的状态 Xi=(x1，x2，…，xn)，其中xi(i=1，2，…，n)为待优化变量;第i条人工鱼当前所在位置的食物浓度即目标函数Yi;人工鱼个体之间的距离为di，j;人工鱼的感知范围为Visual;人工鱼移动的最大步长为Step;拥挤度为delta;觅食行为尝试的最大次数为try_number;当前觅食行为次数为n;最大迭代次数为MAXGEN。

1)觅食行为

设Xi为人工鱼当前的状态，Xj为其感知范围Visual内随机选择的一个状态，如果待优化问题是求极大值，则当Yi＜Yj时人工鱼向Xj方向前进1步(若待优化问题是求极小值，则当Yi＞Yj时人工鱼向Xj方向前进1步);反之，在感知范围内重新选择状态Xj，判断是否满足上述条件。当尝试次数达到最大值try_number时，若仍未找到满足条件的Xj，人工鱼则随机移动1步。

2)聚群行为

对于人工鱼探索当前范围内(即di，j＜Visual)的伙伴数目nf及中心位置Xc，若满足Yc/nf＞delta*Yi，则表明伙伴中心的食物浓度较高并且人工鱼数量不多，则人工鱼朝伙伴的中心位置方向移动1步;否则执行觅食行为。

3)追尾行为

对于人工鱼探索当前范围内(即di，j＜Visual)的伙伴数目nf及食物浓度最大的伙伴Xj，若满足Yj/nf＞delta*Yi，则表明伙伴Xj处的食物浓度较高并且周围人工鱼数量不多，则人工鱼朝伙伴Xj位置方向移动1步;否则执行觅食行为。

4)随机行为

随机行为即人工鱼在Visual内随机选择一个移动方向Xi ext，人工鱼按如下公式进行该行为:

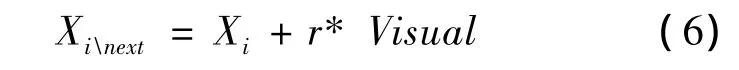
其中r是［－1，1］区间内的随机数。

2.3 WSN 定位原理

假设在一定区域内布置有M个锚节点，N个未知节点。锚节点的坐标为Ai(xi，yi)，i=(1，2，…，M)，未知节点的坐标为Nj(xj，yj)，j=(1，2，…，N)，已知锚节点和未知节点的距离测量值di。基于测距的WSN定位问题可描述为如下的最优化问题:

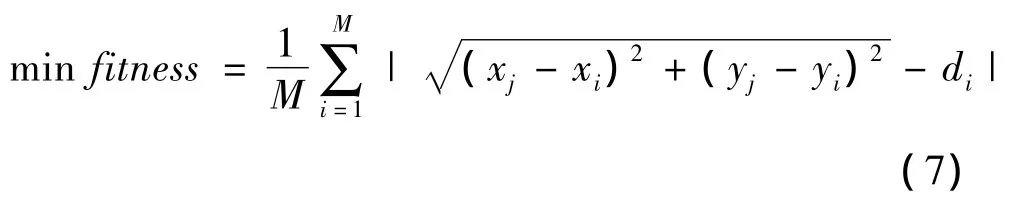
基于群体智能优化的WSN定位方法采用式(7)作为适应度函数，WSN的锚节点相当于该算法中的种群S，未知节点的坐标即要搜索的位置。

3 基于粒子群和人工鱼群融合优化的WSN定位算法

3.1 算法基本思想

PSO算法和AFS算法都是典型的群体智能优化算法。PSO算法具有收敛速度快的特点，但在算法后期，由于粒子同一化，算法易陷入局部最优;AFS算法寻优速度较快，并具有全局寻优的能力，但算法精度略低于PSO算法。综合利用两种算法的优点，提出一种适合WSN定位的粒子群和人工鱼群融合优化(hybrid optimization algorithm based on particle swarm and artificial fish swarm algorithm，PSO-AFS)算法，该算法能克服两种算法各自存在的缺点。

3.2 算法分析和实现

PSO-AFS算法的具体执行过程如下:

1)初始化种群S。在寻优区域内随机或固定部署一个大小为S的种群，合理设置PSO算法和AFS算法各变量的参数，算法的参数设置如下:

① 对于PSO 算法，c1=c2=2，vmax=5，vmin=－5，wmax=0.9，wmin=0.4;

② 对于AFS算法visual=3.5，step=1，delta=0.618，try_number=50;

③PSO-AFS算法的参数与PSO算法和AFS算法对应的参数相同。

2)设置公告板。公告板数值为besty，用来记录每次迭代产生的适应度函数的最优值，公告板初值为初始化的种群S对应的适应度函数值。

3)迭代寻优。在每次迭代中对种群分别用PSO算法、AFS算法进行操作，PSO算法每次迭代得到适应度函数最优值为T1，AFS算法每次迭代得到适应度函数最优值为T2。

4)种群变异。分别对两种算法各自种群个体的适应度函数值排序，对其中最差的30%个体按式:X=bestx+rand进行变异操作，PSO算法和AFS算法各自更新种群，分别得到新的种群S1、S2。

5)更新公告板和种群。比较两种算法得到的适应度函数最优值T1和T2，对公告板和种群进行更新，其伪代码如下:

6)停止迭代，输出结果。当寻优的误差小于控制值或达到最大迭代次数MAXGEN时停止迭代，输出寻优结果及其对应的种群个体的状态，即未知节点位置。

4 算法仿真与分析

本文采用Matlab进行仿真实验，分别考虑两种仿真环境:①在一定区域内进行单个未知节点定位;②模拟具体环境，在一定区域内铺设大量未知节点进行整体定位。

4.1 仿真场景1

在30 m×30 m的面积内随机部署8个锚节点，1个未知节点，节点通信半径为30 m，算法的最大迭代次数MAXGEN为50次。

1)算法稳定性和收敛速度仿真结果分析

设定位误差控制值为0 m，测距误差为10%。图1是3种算法的收敛曲线，由图可知:PSO-AFS算法的收敛曲线与PSO算法、AFS算法相比始终更加平滑、稳定，且收敛速度明显快于另外两种算法。

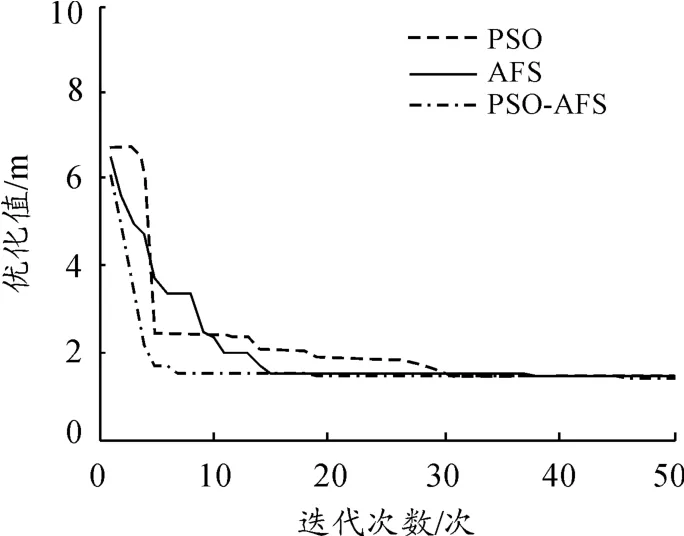
图1 算法的收敛曲线

设平均定位误差(误差控制值)为0.5 m，测距误差0%，独立进行20次实验，分析每次实验中3种算法的终止迭代次数。由图2可知:相同精度下PSO-AFS算法每次最终迭代次数的值波动较小，说明PSO-AFS算法的稳定性较好，明显优于另外两种算法。

2)算法的定位精度仿真结果分析

为了验证基于PSO-AFS算法的无线传感器网络定位算法的性能，设置不同仿真参数，研究迭代次数和测距误差对定位误差的影响，分别独立进行100次实验。

设测距误差为0%，设置不同最大迭代次数进行仿真实验。图3为3种算法的平均定位误差随迭代次数的变化情况。由于PSO-AFS算法的收敛速度明显快于AFS、PSO两种算法，所以在迭代次数较少的情况下，PSO-AFS算法的定位精度明显高于其他两种算法，体现了PSO-AFS算法的优越性。由于PSO-AFS算法在进行迭代寻优时收敛速度和寻优精度性能更好，用较短的计算时间即可得到较精确的计算结果。

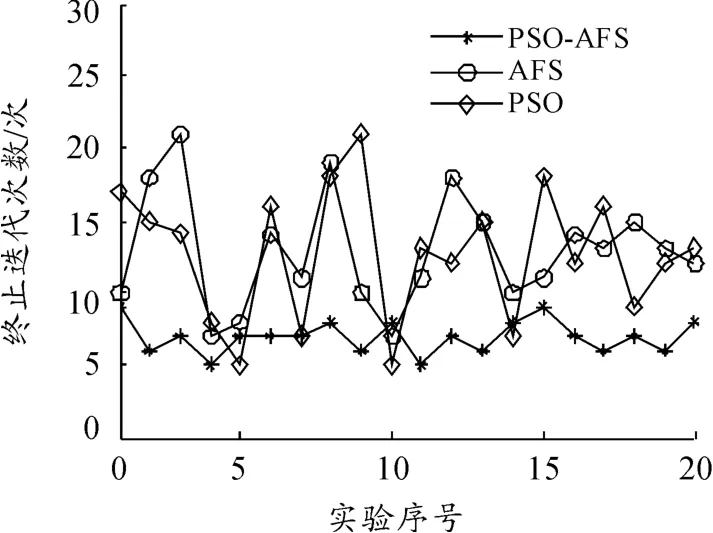
图2 算法的终止迭代次数

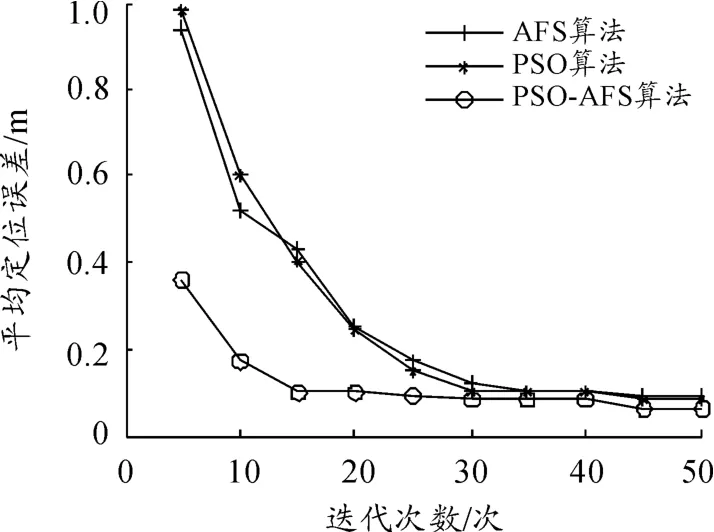
图3 迭代次数对平均定位误差的影响

设最大迭代次数MAXGEN为10次，研究3种算法在不同测距误差情况下的定位精度。由图4可知，随着平均测距误差的增加，3种算法的定位误差均呈上升趋势，这是由于基于测距的定位算法受测距误差影响较大造成的。尽管3种算法的定位误差均受测距误差影响较大，但PSO-AFS算法的定位误差始终小于其他两种算法。PSO-AFS算法与PSO算法相比平均定位误差减小了0.6 m左右，与AFS算法相比平均定位误差减小了0.4 m左右。

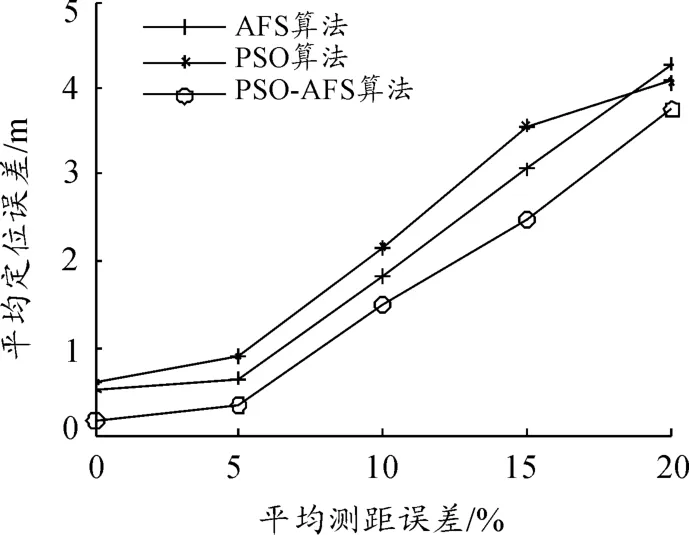
图4 平均测距误差对平均定位误差的影响

4.2 仿真场景2

改变传感器节点部署区域和节点数目，在100 m×100 m的二维平面内随机部署n个锚节点和30个未知节点;节点通信半径为30 m;设最大迭代次数MAXGEN为20次;RSSI测距算法中，设信道衰减指数n为4，为了尽量模拟实际环境噪声的影响，设零均值高斯随机噪声变量Xδ的标准差δ为4。

图5为未知节点平均定位误差随锚节点个数的变化情况，由图可知:随着锚节点数目的增加，3种算法的平均定位误差均呈下降趋势，但当锚节点个数增加到一定程度时，平均定位误差的变化趋势减小甚至达到了临界状态，但PSO-AFS算法的平均定位误差始终小于其他两种算法的平均定位误差。

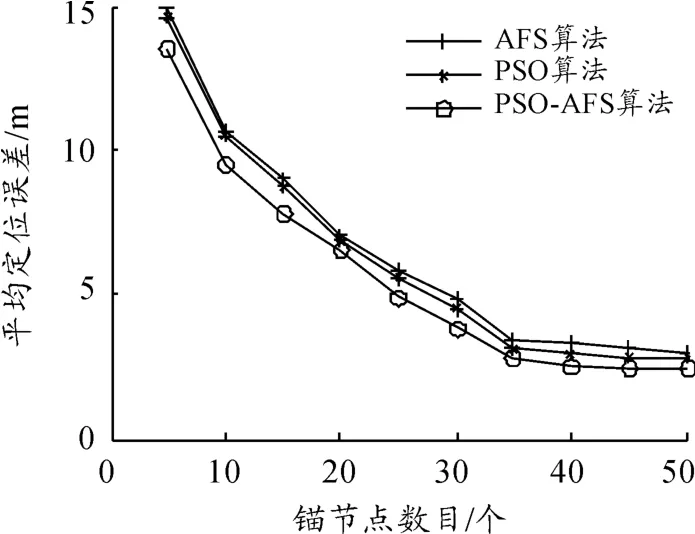
图5 锚节点数目对平均定位误差的影响

5 结束语

由于单一智能优化算法存在不同的性能缺陷，基于单一智能优化算法的WSN定位算法也存在着不足。PSO算法收敛速度快、寻优精度高，但后期易陷入局部最优，导致个别时候寻优结果较差;AFS算法的稳定性较好，全局寻优能力强，不易陷入局部最优，但其收敛速度慢于PSO算法，且寻优精度略低于PSO算法。PSO-AFS算法综合利用了PSO算法收敛速度快、寻优精度高和AFS算法全局寻优能力强、稳定性好的优点，克服了各自存在的不足。基于PSO-AFS算法的WSN定位算法比基于单一PSO算法或AFS算法的WSN定位算法的性能更加优越。仿真结果表明:PSO-AFS定位算法只需较少的迭代次数即可得出较准确的定位结果，且定位精度和稳定性较好，适合于WSN的应用。

［1］宋文，王兵，周应兵，等.无线传感器网络技术与应用［M］.北京:电子工业出版社，2007:1－10.

［2］李晓维，徐勇军，任丰原.无线传感器网络技术［M］.北京:北京理工大学出版社，2007:191－192.

［3］Al-Jazzar Saleh，Ghogho Mounir，McLernon Desmond.A joint TOA/AOA constrained minimization method for locating wireless devices in non-line-of-sight environment［J］.IEEE Transactions on Vehicular Technology，2009，58(1):468－472.

［4］方震，赵湛，郭鹏，等.基于RSSI的测距分析［J］.传感技术学报，2007，20(11):2528－2530.

［5］Savvides A，Han C C，Strivastava M B.Dynamic Fine-Grained Localization in Ad-Hoc Networks of Sensors［C］//Proc.of MOBICOM.［S.l.］:［s.n.］，2001:166－179.

［6］Low K S，Nguyenh A G.Optimization of sensor node locations in a wireless sensor network［C］//ICNC’08 4th Int Conf on Natural Computation.Piscataway:IEEE，2008:286－290.

［7］陈志奎，司威.传感器网络的粒子群优化定位算法［J］.通信技术，2011，44(1):102－104，108.

［8］黄艳，臧传治，于海斌.基于改进粒子群优化的无线传感器网络定位算法［J］.控制与决策，2012，27(1):156－160.

［9］冯秀芳，吕淑芳.基于RSSI和分步粒子群算法的无线传感器网络定位算法［J］.控制与决策，2014，29(11):1－7.

［10］王俊，李树强，刘刚.无线传感器网络三维定位交叉粒子群算法［J］.农业机械学报，2014，45(5):233－238.

［11］陈维克，李文锋，首珩，等.基于RSSI的无线传感器网络加权质心算法定位［J］.武汉理工大学学报，2006，30(2):265－268.

［12］张先超，刘兴长，张春园.基于次锚节点的无线传感器网络改进加权质心定位算法［J］.传感器与微系统，2015，34(2):143－146.

［13］Chen W，Mei T，Sun L，et al.Error analyzing for RSSI-based localization in wireless sensor networks［C］//Intelligent Control and Automation，2008.WCICA 2008.7th World Congress on.IEEE.［S.l.］:IEEE，2008:2701－2706.

［14］史峰，王辉.MATLAB智能算法30个案例分析［M］.北京:北京航空航天大学出版社，2011:102－107.

［15］李晓磊.一种新型的智能优化方法—人工鱼群算法［D］.杭州:浙江大学，2003.