浅谈铁路客运专线高程上桥技术

张飞，张杰胜 （中铁四局集团第一工程有限公司，安徽 合肥 230041）

0 前 言

为保证铁路客运专线轨道工程高平顺性，对客运专线建设时期的高程测量尤其重要，根据合（肥）蚌（埠）、石（家庄）武（汉）铁路客运施工测量经验，本文对无砟轨道施工高程控制网测量中的误差来源及精度进行了分析，并对高程测量方法进行了一些改进，以满足客运专线对轨道高平顺性的要求。本文着重对高程上桥测量和轨道工程CPⅢ控制网高程测量进行阐述。

1 三角高程测量

客运专线大量的线路是以桥梁为主，将桥下的水准点高程引入到桥面上，俗称高程上桥测量。在施工中，常采用全站仪三角高程测量的方法进行。

1.1 全站仪精密三角高程测量原理

三角高程测量是通过观测两点间的水平距离和天顶距（或高度角）求定两点间的高差的方法。它观测方法简单，不受地形条件限制，是测定大地控制点高程的基本方法。如图1 所示，S为A、B 两点的斜距，在A 点安置仪器，i 为仪器高。在B 点安置觇标，觇标高位v。R 为地球曲率半径，取近似R=6370km。根据精密三角高程测量原理有：

其中：HAB——A、B 两点高差

K——A 至B 方向的大气折光系数

α——竖直角

1.2 精密三角高程测量误差来源及影响

根据精密三角高程测量公式，结合以往经验，三角高程测量的误差来源于以下几个主要方面。

1.2.1 地球曲率的影响计算误差

地球曲率影响Δ地曲的计算公式为：

地球是不规则的球体，严格的说不同地区R 的值不同。在S·cosα（即平距）较大的情况下对三角高程精度产生不可忽略的影响，当S·cosα=50m，Δ地曲=0.2mm；当S·cosα=100m，Δ地曲=0.78mm；当S·cosα=500m，Δ地曲=19.62mm。

1.2.2 大气折光的影响

大气折光影响Δ大气折光的计算公式为：

大气折光系数K 与为大气遮光曲率半径R'成反比关系。R'受光线经过的路径的环境影响，例如温度、湿度等，R'是一个不断变化的值。在水准跨河测量过程中，光线要经过湿度、温度等外界环境变化较大的水面，这样折光系数在路径上不仅不是常值，且变化很大，在目前的技术条件下，精确计算出K 值是不可能的，一般用近似值带入计算，这样就产生了系统误差。根据经验，此项误差可达1mm～3mm。

1.2.3 仪器高、觇标高的量取误差、对中误差

仪器高和觇标高的一般采用钢尺法量取，钢尺的最小分化值为1mm，可以估读到0.1mm。实际操作过程中，受温度、拉力的影响，钢尺还会产生变形，根据经验，仪器高和觇标高的量取误差可达1mm～2mm。

1.2.4 瞄准误差

受人眼的分辨能力的限制，仪器瞄准目标的误差可达1mm～2mm。

1.2 .5测角、测距误差

三角高程计算是建立在测角、测距基础上的，测角、测距的误差直接影响三角高程的测量精度。

根据上述因素的影响，用三角高程直接进行二等水准上桥测量，其精度是不能达到二等水准测量的要求，必须对测量设备和测量方法予以改进，下面介绍一种全站仪中间法三角高程测量。

2 中间法三角高程测量

2.1 全站仪中间法三角高程测量原理

全站仪中间法三角高程测量是将全站仪置于已知高程点和待测高程点中间，在不量取仪器高的情况下，利用三角高程测量原理测出待测点的高程。这种方法因全站仪到待测点和已知点的平距大致相等，可大大削弱由地球曲率和大气折光所带来的误差，如图2所示。

如图2 中，假设A 为已知高程点，B 为待测高程点，在距离A 点和B 点大致相等的位置C 点安置全站仪，根据三角高程测量原理，可以得到：

式中：S1为C 点到A 点的斜距；α1为C点至A点的竖直角；f1、f2分别为C 至A 点的地球曲率改正数和大气折光系数改正数；i 为仪器高；l1为A 点的棱镜高。将地球曲率改正数、大气折光系数改正数代入式(1)，设K1为C 至A 点的大气折光系数，R 为地球半径，则式(3)可表示为：

同理：

式中：S2为C 点到B 点的斜距；α2为C 至B 点竖直角；f'1、f'2分别为C 至B 点的地球曲率改正数和大气折光系数改正数；i 为仪器高；l2为A 点的棱镜高。设K2为C 至B 点的大气折光系数，则式(5)可表达为：

将A、B 两点设置的棱镜高设置成等高，即l1=l2，则A、B 两点的高差为：

此时D2=S2cosα2，D1=S1cosα1，则式(7)可写为：

2.2 全站仪中间法三角高程测量中误差分析

根据误差传播定律，对式(8)进行微分，可得：

从式(10)中可以看出，误差仅与测角、测距精度有关。例如采用徕卡1201+全站仪进行观测，仪器标称精度：则mα=±1''，ms=±（1+1.5×10-6·S）mm，由于D=S cosα，所以由于很小可以忽略，故得取0.14，又因对高差中误差的影响与所测边长的平方成正比，所以D1、D2不宜过长，在实际应用中由于仪器自身的条件以及二等水准要求，D1、D2的距离不超过60m，此时可忽略不计，则式(10)可写为：

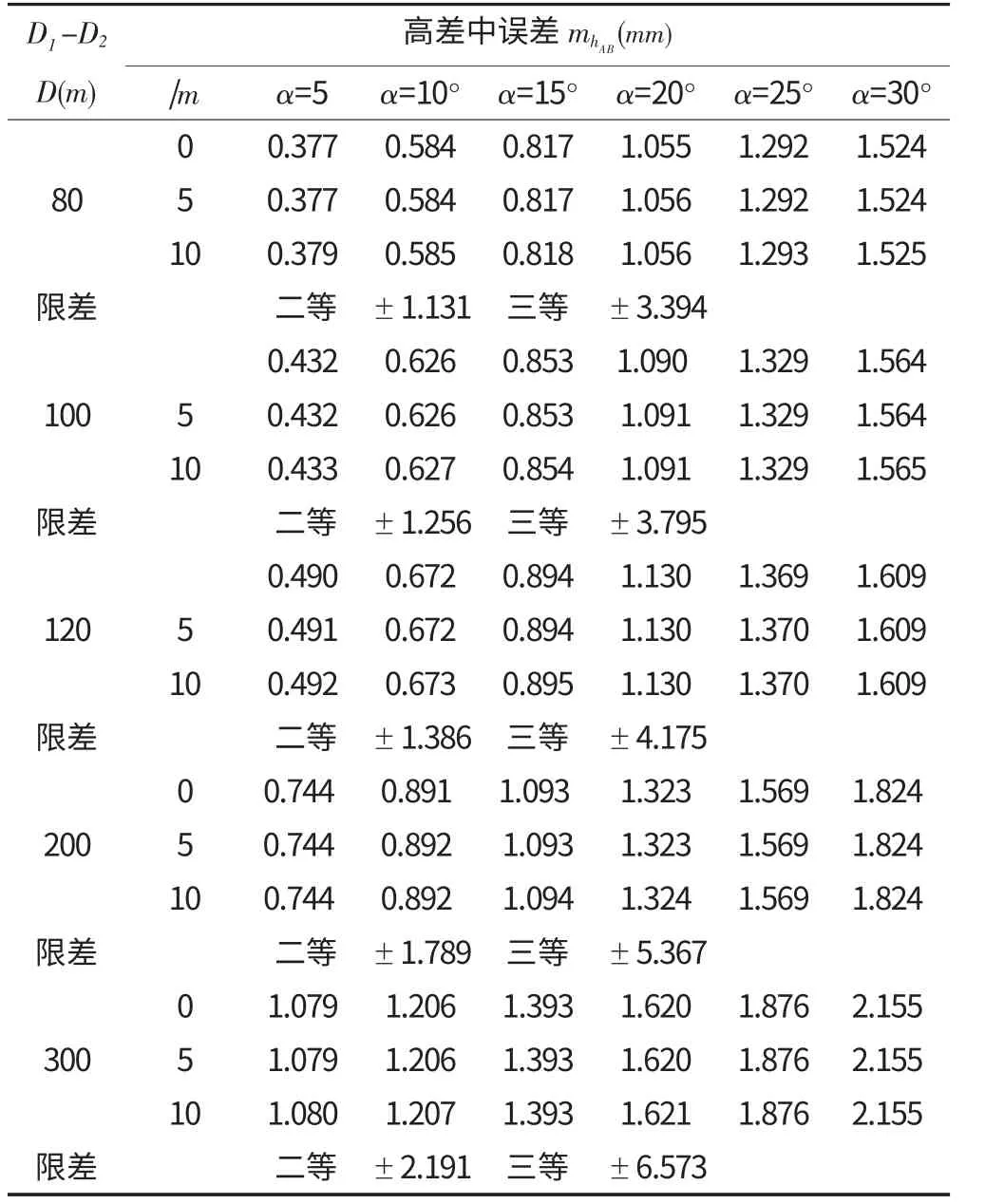
全站仪中间法三角高程测量的高差中误差 表1

上式取mK=±0.04，取不同的平距和竖直角度，按式(11)计算的高差中误差，见表1。

由表1可知，全站仪中间法三角高程测量高差中误差随着距离和竖直角的增大而增大，由于测角误差对高差中误差的影响与水平距离有关，测距误差对高差中误差的影响要远小于测角误差对高差中误差的影响。此时将2倍的中误差和二等、三等水准测量的限差进行比较，当α≤10°、D≤200m 时全站仪中间法的测量精度可达到二等精度要求；当α≤5°、D≤300m 时也可达到二等精度要求。

3 全站仪中间法三角高程测量与水准仪测量的比较

为了检验全站仪中间法在实际工程中是否能达到二等的精度要求，实验选取一闭合环，如图3所示。分别利用全站仪和水准仪施测，起始点A 的高程定为0.000m，先利用天宝Dini电子水准仪进行往返测量，平差后，求出每测站的高差作为两点间高差的准真值；然后利用全站仪中间法进行观测，得出两点间的高差与准真值进行比较，比较两者之间的差值是否在限差之内，同时判定高差闭合差是否达到二等要求，实验结果如表2所示。

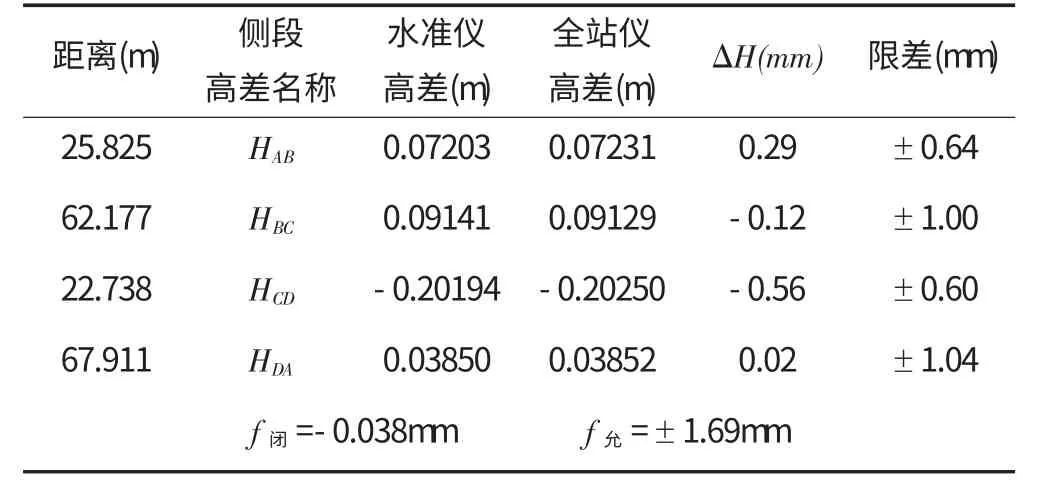
全站仪中间法三角高程测量与二等水准测量结果的比较 表2

从表2可知，水准仪所测高差和全站仪所测高差的差值均在限差范围之内，且高差闭合差也在允许范围之内，所以全站仪中间法应用于二等水准测量是可行的。此外，为了检测前后视距差对全站仪中间法测量的影响，本文选取了80m和160m两段直线，分别在前后视距差为0m、3m、5m、10m时进行高差测量，并与水准仪所测的高差进行比较，检查两者高差之差是否在限差之内，从而判断视距差对全站仪中间法测量的影响，实验结果如表3所示。

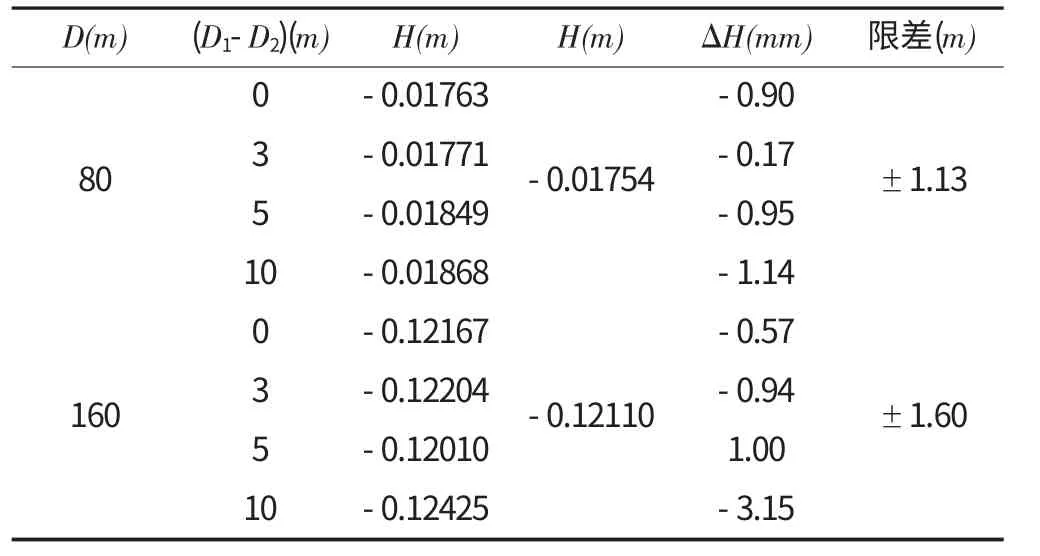
前后视距差对全站仪中间法三角高程测量的影响 表3

由表3可知，当前后视距差在5 m内时，所测的高差均在限差范围之内。所以在利用全站仪中间法替代二等水准测量时，应将前后视距差控制在5m之内，以便达到所需的测量精度。

4 结 语

本文通过研究全站仪中间法三角高程测量的误差来源及其影响，并对测量精度进行分析，得出了全站仪中间法三角高程测量在竖直角α≤10°、两点水平距离D≤200m 时可以代替二等水准测量，且当α≤5°、D≤300m 时，也能达到二等精度要求。通过实验，验证了用全站仪中间法替代二等水准测量的可行性，得出在全站仪中间法代替二水准测量时应将前后视距差控制在5m之内，从而可尽量的减小地球曲率以及大气折光带来的误差。

随着我国高铁的大量建设，并逐渐走出国门，无碴轨道精密测量技术在施工过程中要求将更高，在高铁的日常养护过程中要保持轨道的高平顺、高稳定性也离不开轨道精密测量，无砟轨道施工三级平面控制网建立的准确性与精确性，将为高铁的前期施工控制和后期维护管理中精密测量提供坚实的保障。

[1]TB10601-2009,高速铁路工程测量规范[S].北京：中国铁道出版社，2009.

[2]铁建设[2006]189号,客运专线无碴轨道铁路工程测量暂行规定[S].

[3]铁建设［2007］85号,客运专线无砟轨道铁路工程施工质量验收暂行标准[S].

[4]经规标准[2007]100号,客运专线无碴轨道铁路工程施工技术指南[S].

[5]GB/T 12897-2006,国家一、二等水准测量规范[S].北京：中国标准出版社，2006.

[6]GB50026-2007,工程测量规范[S].北京：中国计划出版社，2007.

[7]GB/T 15314-1994,精密工程测量规范[S].北京：中国标准出版社，1994.

[8]GB/T18314-2001,全球定位系统GPS测量规范[S].北京：中国标准出版社，2001.