对一类极小谱任意符号模式的刻画

乔晓玲,邵燕灵

(中北大学 理学院,山西 太原,030051)

1 相关知识与理论

符号模式矩阵是元素取自集合{0,+,-}的矩阵,简称符号模式,其中“+”代表正元素,“-”代表负元素。对于给定的实矩阵 B=(bij),由B中的每个元素 bij的符号所确定的矩阵A称为B的符号模式,记为sgn(B)。 Q(A)={ B=(bij)|sgn(B)=A}称为由A决定的定性矩阵类,表示所有与A有相同符号模式的实矩阵的集合。

定义1[1]令 S=(sij)和A=(aij)是2个n阶符号模式矩阵,如果当 aij≠0 时,sij=aij,则称 S=(sij)是 A=(aij)的母模式,A=(aij)是S=(sij)的子模式。如果A≠S,则称A是S的真子模式。

定义2[1]设A为1个n阶符号模式矩阵,如果存在B∈Q(A)和正整数k,满足Bk=0,而Bk-1≠0。则称A蕴含幂零,其中B为幂零矩阵。

定义3[2]对于n阶符号模式矩阵A,若每一个矩阵B∈Q(A)是奇异的,则称A是符号奇异的; 若任一矩阵B∈Q(A)是非奇异的,则称A是符号非奇异的。

定义4[2]如果 f(x)为任意给定的一个n次首一实系数多项式,A为n阶符号模式矩阵,若满足特征多项式等于f(x)的实矩阵P存在,且P∈Q(A),则称符号模式矩阵A为谱任意的。若A的任意一个真子模式都不是谱任意的,那么A是极小谱任意的。

引理1(幂零–雅可比方法)[3]A为n阶符号模式矩阵,如果符号模式A蕴含幂零矩阵B∈Q(A),

文献[1]中介绍了目前关于符号模式矩阵研究的基本定义及定理。最早由文献[2]给出了符号模式矩阵的概念,幂零–雅可比方法也是在该文献中提出的,并给出了如何用幂零–雅可比方法来证明一个符号模式矩阵及其母模式都是谱任意的。文献[3–9]对符号模式矩阵的谱任意进行了深入的研究。

2 主要结果

定理1 当 6n≥时,符号模式A是蕴含幂零的。

证明 任取实矩阵()Q∈B A,设B的形式如下:将上述行列式中第i行的x倍加到第 i+1 行,i=1,2,…,n-4,再按第2,3,…,k-1,k+ 1,…,n-3列展开,可得

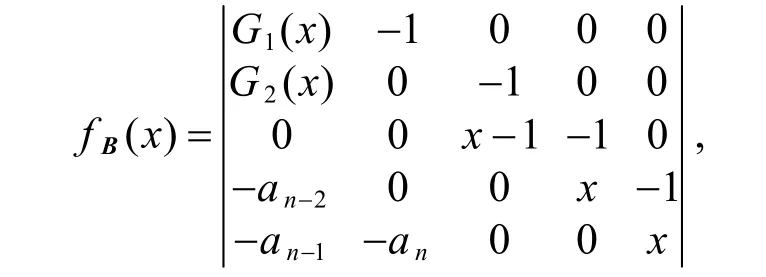
定理2 当 6n≥时,符号模式A及其所有母模式都是谱任意的。

证明 由定理1知

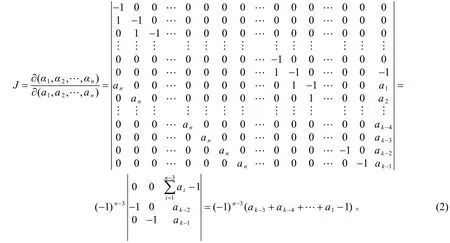
由引理1知,符号模式A及其所有母模式都是谱任意的。

定理3 当 n≥6 时,符号模式A是极小谱任意的。

证明 设 T=(tij)n×n是A的一个真子模式,且T是谱任意的。

(1)tn-2,n-2≠0,否则T的迹为负,与T是谱任意相矛盾;

(2)ti,i+1≠0(i=1,2,…,k-2,k,…,n-1),否则T是符号奇异的,与T是谱任意相矛盾;

(3)tk-1,k≠0,否则T是符号非奇异的,与T是谱任意相矛盾;

(4)ti,1≠0(i=1,2,…,n-3,n-1,n),tn,k≠0,否则不存在B∈Q(A)是幂零矩阵,与T是谱任意矛盾。综合以上可知A是极小谱任意的。

[1]Leslie H.Handbook of linear algebra [M].Bocaraton:CRC Press,2007.

[2]Drew J H,Johnson C R,Olesky D D,et al.Spectrally arbitrary patterns [J].Linear Algebra and Its Applications,2000,308:121–137.

[3]Britz T,Mcdonald J J,Olesky D D,et al.Minimally spectrally arbitrary sign patterns[J].SIAM Journal on Matrix Analysis and Applications,2004,26(1):257–271.

[4]Mcdonald J J,Olesky D D,Tsatsomeros M J,et al.On the spectra of striped sign patterns [J].Linear and Multilinear Algebra,2003,51(1):39–48.

[5]Cavers M S,Vander Meulen K N.Spectrally and inertially arbitrary sign patterns [J].Linear Algebra and Its Applications,2005,394:53–72.

[6]Gao Yu-bin,Shao Yan-ling.A spectrally arbitrary pattern [J].Advances in Mathematics,2006,35(5):551–555.

[7]Gao Yu-bin,Shao Yan-ling,Li Zhong-shan.A note on spectrally arbitrary sign patterns [J].JP Journal of Algebra,Number Theory and Applications,2008,11:15–35.

[8]Gao Yu-bin,Shao Yan-ling.New classes of spectrally arbitrary ray patterns [J].Linear Algebra and Its Applications,2011,434:2 140–2 148.

[9]Bergsma H,Kevin N,Vanderm,et al.Potentially nilpotent patterns and the Nilpotent-Jacobian method [J].Linear Algebra and Its Applications,2012,436:4 433–4 445.