流量具导向性的大中型城市交通拥堵的探究与治理

张晓颖 于琪琪

(长春大学理学院，长春130022)

0 引言

高速发展的中国大中型城市在见证经济增长的同时，也面对着由地区经济发展所导致的周边人口的大量涌入和城市道路规划的滞后。由于分区的不同以及特定地形与人文环境的不同，导致不同状态的交通拥堵。道路交通拥堵治理方案的研究在我国大中型城市发展中占据非常重要的位置。

深圳市在2010年颁布的《深圳市规划轨道交通规划(2010－2020)》中，指出了深圳市轨道交通的层次划分:国家与区域线路、市区干线、局域线。并根据这三种层次对轨道网络布局进行了规划［1］。本文根据《规划》［1］中的相关数据，对深圳市关口交通拥堵问题进行建模分析，进而给出城市交通拥堵治理的建议。

1 数据采集侧重及交通拥堵分析过程

1.1 基于交通规划的道路拥堵分析模型

路网中所有路段和交叉口的拥堵程度是交通设施负荷程度的综合评价指标。其中路段的拥堵程度可以用路段平均车速、路段平均延误、路段平均饱和度三个指标来衡量;交叉口的拥堵程度可以用交叉口平均转向延误和交叉口平均饱和度两个指标来衡量。本文对衡量交通拥堵的以上指标进行层次分析，建立两层因子，如图1所示，并最终得到路网整体交通拥堵度，分析造成拥堵的直接原因并提出相关建议。

先用标度法对各层次权重因子进行标度。得出第一层次的重要性判断矩阵(表1)，用同样的方法，得出属于第二层次的重要性判断矩阵(表2):

表1 第一层次判断矩阵

表2 第二层次路段因素判断矩阵

表3 第二层次交叉口因素判断矩阵

由以上结果得出三个权重矩阵:

图1 拥堵评判层次分析

设交通拥堵评判集为{1，2，3，4，5}，1 表示畅通，5 表示严重堵塞，则路段和交叉口各个影响因素的隶属函数分析如下:

1.1.1 路段平均速度影响因素

速度V的隶属函数采用偏小型岭分布。本文主要研究深圳市三种道路及其交叉口平均速度的隶属函数，以梅林关为例，这三种道路分别是快速路(南坪快速路)、主干路(梅观路、梅坂大道、彩田路)、次干路(梅龙路、皇岗路、民治路)。并根据深圳市道路规模［2］确定。

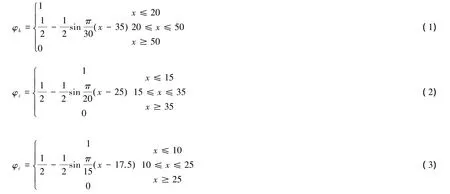
由公式(1)、(2)和(3)得出图2

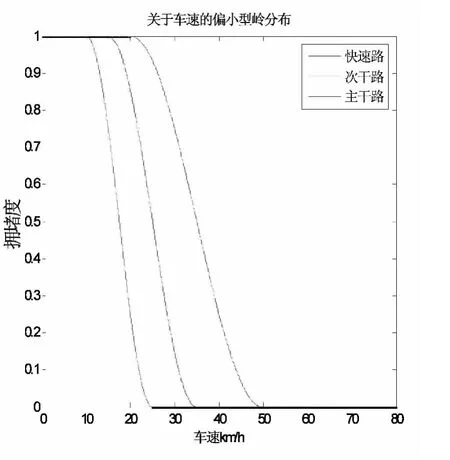
图2 平均车速岭分布图

图3 路段平均延误岭分布图

由图2可得速度的拥堵等级:

1.1.2 路段平均延误影响因素

在瓶颈路段用调查交通量的方法，以1小时为间隔，累计交通量。

分别由梅林关主干路、次干路、快速路所采集的数据绘制成表，再将表中数据分别绘成车辆到达、离去曲线，两曲线与x轴所围成的面积差即为所有受阻车辆通过瓶颈路段所需总时间，记为Da。当车辆不受阻时通过瓶颈路段所需时间与受阻车辆通过瓶颈路段所需时间相比比较小时，可认为Da是受阻车辆的总延误时间为

所以每辆车通过瓶颈路段的平均行车时间为

当无堵塞时，每辆车所需行驶时间为

所以每辆车的平均延误为

路段平均延误的隶属函数采用偏大型岭分布函数。本文主要研究深圳市三种道路平均延误的隶属函数，以梅林关为例，这三种道路分别是快速路(南坪快速路)、主干路(梅观路、梅坂大道、彩田路)、次干路(梅龙路、皇岗路、民治路)。并根据深圳市道路规模［3］确定。

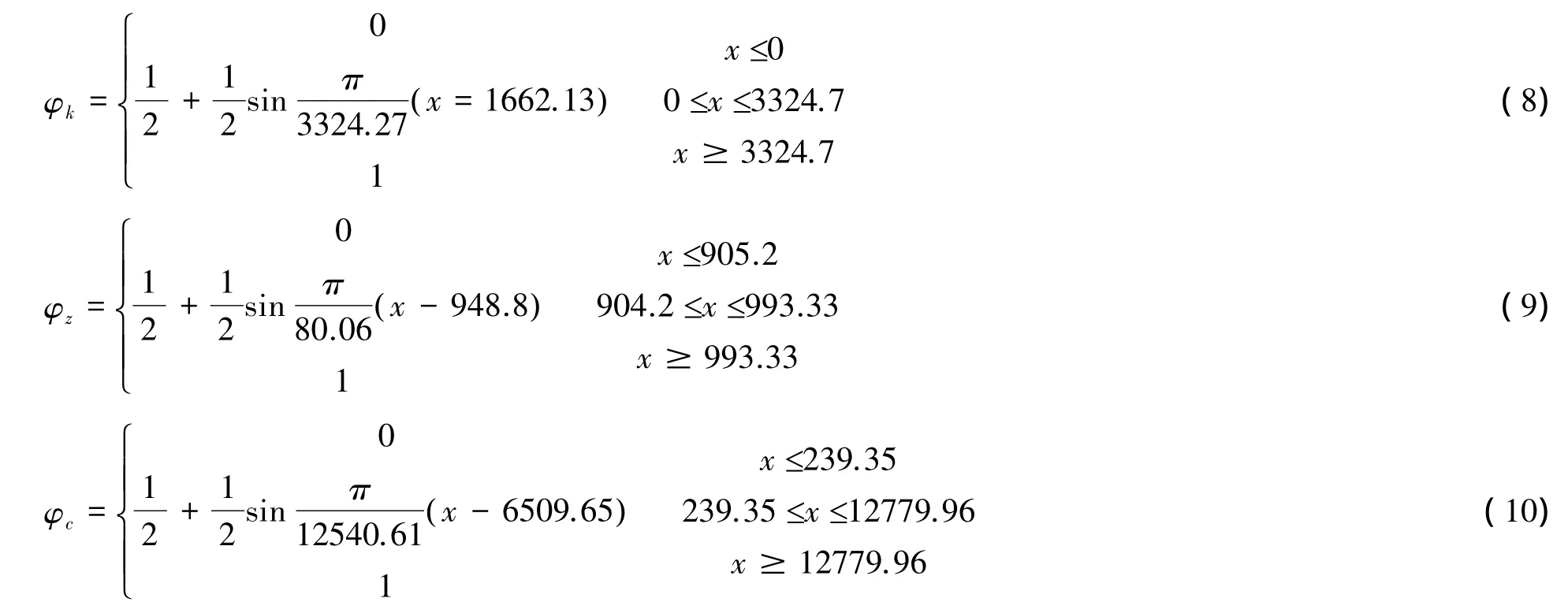
由式(8)、(9)和(10)得出图3，由图3可得道路平均延误的拥堵等级:

1.1.3 路段平均饱和度

路段平均饱和度N的计算公式为:

通行能力的计算公式为:

车道所属信号相位的绿信比计算公式为:

路段平均饱和度N的隶属函数采用偏大型岭分布函数。本文主要研究深圳市两种道路平均饱和度的隶属函数，以梅林关为例，这两种道路分别是快速路(南坪快速路)、主干路(梅观公路、梅观高速)。

相应快速路和主干路的偏大型岭分布函数:

由式(14)和(15)得出图4

图4 路段饱和度偏大型岭分布图

图5 交叉口平均延误岭分布图

由图4可得饱和度的拥堵分级为:

1.1.4 交叉口平均饱和度

交叉口平均饱和度可根据路段平均饱和度加权平均求出。

交叉口平均饱和度M的隶属函数采用偏大型岭分布。本文主要研究深圳市交叉口平均饱和度的隶属函数，以梅林关为例。由处理后数据及计算公式可得相应交叉口平均饱和度的偏大型岭型分布函数:

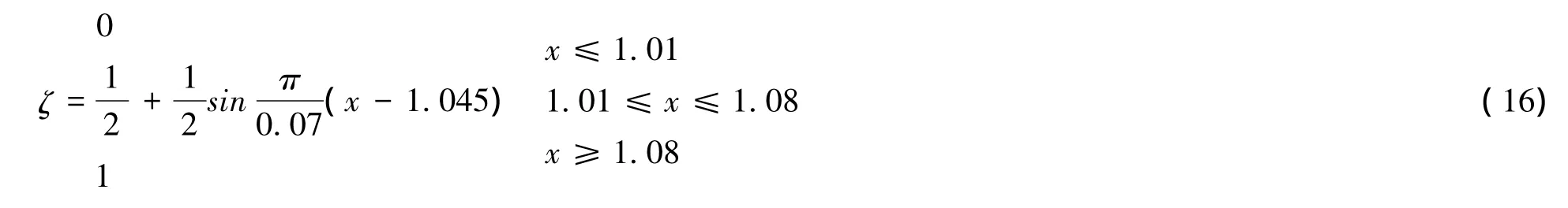
由式(16)得出图5，由图5可得交叉口平均饱和度的拥堵分级为:

1.1.5 交叉口平均延误

对于交叉口平均延误的计算本文采用交叉口延误的概率统计模型:

a.基本假设

(1)假设某时段信号灯周期为C，且此时段内信号灯周期保持不变。g为绿灯时长，r为红灯时长(本文不考虑黄灯，即C=r+g)。令此Mi为时段内的交叉口平均饱和度，到达交叉口停车线的车辆数为q，且服从泊松分布。另μi为q的数学期望，这时，μi是Mi的理论上的平均交通量。当平均饱和度为Mi时，各信号周期C内到达车辆数q可能的取值为1，2，…，qc(q=0时无意义)。

其中

式(17)为每周期内到达车流量的饱和值，S为饱和流量，而q取各值的概率为式(18)，q=1，2，…，qc，令q=1，2，…，qc时的概率为 pi，1，pi，2，…，pi，qc。

(2)一个红绿灯信号周期C内，车辆的行为表现为均匀分布。且到达交叉口的每一辆车的停车间隔用信号周期与流量的关系可表示为:C/q+1。

(3)绿灯初始时的入口排队车辆数是定值，并假设车辆排队时，相邻两车的车头时距是t0。

b.延误计算模型

假设红绿灯信号周期C内的到达流量为L0，此时L0也可视作本周期的排队长度的饱和值即式:

此时，若停车次数大于一(即超饱和延误)时，到达量的值q＞L0。设L0为一个信号周期C内，饱和度为1.0时的到达流量，即式(19)，可将L0称为该周期的饱和排队长度，如到达量q＞L0时，认为将会出现超饱和延误(即二次及以上停车)。对于某时段内平均饱和度为Mi的 情况下，即Mi≤1.0时，μi≤L0;当Mi＞1.0时，μi＞ L0，易知 t0=g/L0。

每一信号周期内的延误计算如下:当q=1时，延误为式:

车辆在C/2时到达;当q=2时，延误为式:

车辆分别在C/3和2C/3时到达;……;当q=L0时，停车延误为式:

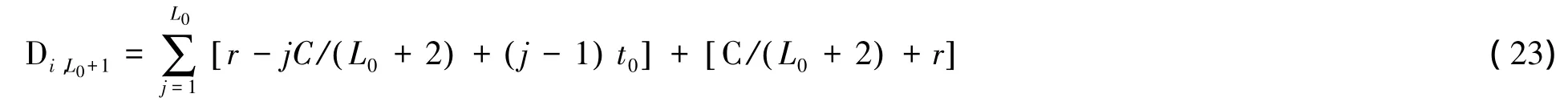
式中第二项为超饱和延误。当q＞L0时，超饱和车辆会产生二次及以上停车。当L0＜q≤2L0时，超饱和车辆产生二次停车。此时的延误为式:

当2L0＜q＜3L0时，超饱和车辆产生三次停车，此时的延误为式(25)。

有一种极端情况，q＞3L0，这意味着最晚到达的车辆会出现第四次停车。在正常情况下，这种状况非常罕见，因此不予考虑。

将第一次、第二次和第三次的停车系数分别设为η1，η2，η3，并由此列出到达交通量为q时的延误通用表达式。

于是得式

据式(22)－(25)可得交叉口到达车流量为q时的延误为式:

于是可得到平均饱和度为Mi时每周期交叉口车辆的平均延误为式:

最终得交叉口平均延误的偏大型岭性分布函数:

由式(29)得出图6:

图6 交叉口平均延误岭分布图

1.1.6 拥堵评判指标的计算结果

由上述描述路段拥堵度的三个指标的评判标准可得以下基于路段因素的评判矩阵

又描述道路拥堵度的指标(平均车速、平均延误和平均饱和度)的权重矩阵为(2.1.31)

则关于路段拥堵度的综合评判为:B1=R1·A1，得矩阵

同理可由上述交叉口拥堵度的两个指标的评判标准得基于交叉口因素的评判矩阵

又描述交叉口拥堵度的指标(平均延误和平均饱和度)的权重矩阵为

则关于交叉口拥堵度的综合评判为:B2=R2·A2，得矩阵

由以上两个单因素评判阵得路网拥堵度评判为式

得矩阵

1.2 基于多速度差的模拟交通流跟驰模型

由司机对车头距的反应速度和邻近车辆在行驶过程中的关系得表达式

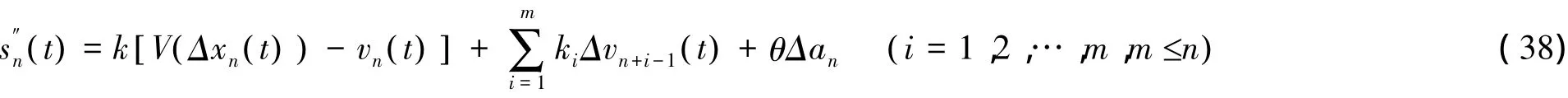
由于本文只需要模拟拥堵路段的交通流，汽车缓行时加速度差异忽略，故得到式

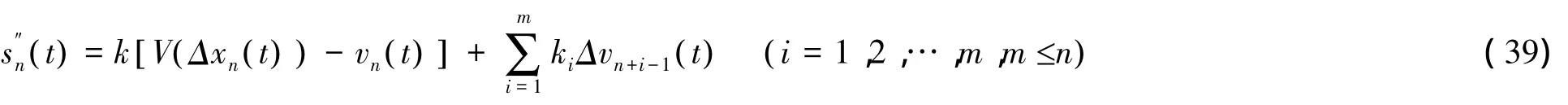
根据二线关口相关处理后数据并、参考交通流广义力模型［7］中实测数据对函数进行数值模拟表达式

其中C1=0.13s－1，C2=1.57s－1是经验参数。由于驾驶员对前车车速的反应时间对模型构成影响，人的平均反应时间为 1－2.2s，取 k=1.4137，k1=0.20，k2=0.15，k3=0.10。同时本文取车道为7 条的梅观公路普滨加油站南行－北－战略道路，和车道为3条的梅龙、民治路－南行入梅观公路口，应用matlab得出图7和图8:

图7 梅关公路普滨加油站－北－战略交通流模拟图

图8 梅龙、民治路－南行如梅关公路口交通流模拟图

上述模型较好地模拟了拥堵情况车速变化情况，就拥堵状况而言，可看出相同时间段内达车道少的道路后到拥堵状况，但较快达到最大车速。

2 数据采集建议及交通拥堵缓解方案

2.1 宏观模型的结论及建议

从宏观角度分析深圳市关口交通拥堵，以梅林关为例，由道路拥堵权重矩阵B1=(0.2541 0.0634 0.1111 0.0477 0.5237)、交叉口拥堵权重矩阵B2=(0.4445 0.1112 0.0555 0.0555 0.3333)，和交叉口平均延误概率统计模型可以看出造成梅林关口拥堵的直接原因是交叉口分配不均衡。

梅林关口总体道路和交叉口的拥堵度由1(畅通)，2(较畅通)，3(较拥堵)，4(拥堵)，5(堵塞)的评判矩阵为式:

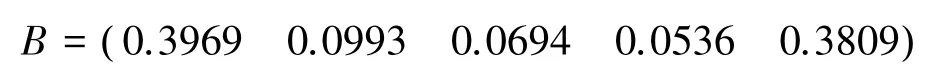
出现了两种极端现象，因此本文对深圳市关口交通数据采集侧重提出了以下建议:

在重点交叉口(如梅林关口的梅观路与彩田路、皇岗北路交叉口和梅观路与梅坂大道、梅龙路交叉口)设立每隔10s的转向延误时间采集器，从而重点检测由交叉口转向延误带来的整体阻塞。

在重点主干路(如梅林关的梅观路、南坪快速路)设立多个延误时间和车速跟车监测点。

2.2 微观模型的结论及建议

从微观角度分析深圳市关口道路交通拥堵，可看出相同时间段内，车道少的道路后到拥堵状况，但较快达到最大车速。为使车辆在道路上行驶平稳，可适当增加车道。本文假设此模型成立的条件是驾驶员的平均反应时间正常，在实际生活中，由驾驶员反映迟钝(如酒驾等)造成的交通拥堵事故不可排除，建议在宏观模型中提出的重点交叉口处适当增加车道，并在进入拥堵高发路短前对驾驶员进行适当检查。

由上述结论可以看出，如果可以增加关内通道，应在交叉口评判矩阵出现严重不均衡处(如梅林关的梅观路与彩田路、皇岗北路交叉口)设置分流道路和通往关内的道路(如将梅龙路直接延伸至关内，改变梅观高速以东车辆转车进入仅有两车道的掉头匝道)。

在不增加关内外通道数量的情况下，可以通过调整城市分区功能(如在方便来往的区域建廉租房或安置房，进行旧村改造，以减少由关外进入关内上班的人口)，改变关口区域功能架构(如改变位于民乐立交桥的西端民乐桥180度掉头匝道;将梅观路与南坪路汇合处的废旧龙门架拆除，以改变由梅观路到南坪路上由6车道变4车道造成的拥堵;改变关口公交车与车站的位置，尽量避免公交车站大量乘客在机动车道等车所造成的拥堵)，改善交通管控措施(如交警提前到岗及时疏导交通;部分路段高峰期实行单双号限行等)。

3 总结

本文以深圳市为例，致力于研究造成大中型城市高峰期具导向性拥堵的直接原因，并据此对拥堵路段的数据采集提出建议。通过用宏观和微观两个模型展开研究，并得出结论:交叉口分配不均衡是导致深圳市梅林关口关内外高峰期瞬时拥堵的直接原因。可以通过增加关内通道或者改变城市分区功能的方式来改善交通拥堵状况。

大中型城市的交通拥堵问题非常复杂，具有导向性的瞬时拥堵的治理问题也涉及到非常多的方面，本文并没有考虑城市相关经济与政治政策调整的影响。

［1］深圳市规划和国土资源委员会.深圳市轨道交通规划(2010－2020)［R］.深圳:深圳市城市交通规划设计研究中心，2009.

［2］李百浩，王玮.深圳城市规划发展及其范型的历史研究［J］.城市规划，2007，31(2):70～76.

［3］中华人民共和国建筑部.城市道路标准规范(CJJ37－90)［S］.北京:中国建筑工业出版社，1991.