SVM和改进的PSO在压路机驾驶室结构噪声优化中的应用

贺建军，付 玲,杨 川，阳 鹏

(1.湘潭大学 机械工程学院，湖南 湘潭 411105；2.中联重科股份有限公司，长沙 410013；3.建设机械关键技术国家重点实验室，长沙 410013）

SVM和改进的PSO在压路机驾驶室结构噪声优化中的应用

贺建军1，付 玲2,3,杨 川2,3，阳 鹏2,3

(1.湘潭大学 机械工程学院，湖南 湘潭 411105；2.中联重科股份有限公司，长沙 410013；3.建设机械关键技术国家重点实验室，长沙 410013）

针对压路机驾驶室结构噪声，将拉丁超立方试验设计、支持向量机近似模型、改进的粒子群优化算法相结合，通过修改驾驶室主要板件的板厚参数降低压路机结构噪声。建立一套基于支持向量机和粒子群算法控制车内结构噪声的设计流程。针对粒子群可能出现局部最优解的问题，对粒子群进行了改进。并利用改进的粒子群优化支持向量机参数，构建高拟合精度的支持向量机模型代替有限元模型。并用改进的粒子群算法对该模型进行板厚寻优，找到一组最佳的板厚参数使得参考点（驾驶员右耳处）声压级最小，减少计算工作量，提高优化效率。

声学；压路机；支持向量机；驾驶室；结构噪声

随着人们对工作环境的要求不断提高，在提高压路机压实性能的同时，如何提高驾驶员乘坐舒适性成为产品研发的关键性问题。在满足工艺和经济条件下，修改车身结构参数是控制与降低车内噪声的有效方法之一。

由于驾驶室噪声有限元分析花费时间长，基于有限元模型进行优化效率低。目前，对于大型模型，基本采用近似模型进行优化。将近似模型代替有限元模型能有效提高计算效率。常用的近似替代模型主要有：响应面模型、Kriging模型、神经网络模型。响应面模型对于高维非线性问题在准确度以及稳定度上有所欠缺[1-3]。Kriging模型是估计方差的最小无偏估计模型，但在高维问题上，Kriging模型需要对复杂的矩阵进行求逆运算，计算成本较高[4]。神经网络容易受到网络结构复杂性以及样本数量等因素的影响，容易出现泛化能力不强等问题[5]。支持向量机（Support Vector Machine，SVM)在统计学理论的基础上提出的一种新的学习算法，支持向量机建立在统计学VC维和结构风险最小化原则的基础上。支持向量机能够有效地解决非线性、小样本以及高维识别问题，具有较好的泛化能力[6-8]。

粒子群优化（Particle Swarm Optimization，PSO)算法是一种基于群体的智能寻优算法，源于对鸟群的捕食行为的研究。粒子群算法具有高度并行、算法易理解且容易编程实现，对目标函数数学形式没有特殊要求等特点，近年来在许多领域得到广泛应用[9，10]。

本文将建立压路机驾驶室板厚作为设计变量，驾驶室1阶扭转模态频率、驾驶室设计变量总质量为约束条件，车内参考点声压响应为目标函数的数学优化模型。将采用支持向量机近似模型，用以替代有限元模型，利用改进的粒子群优化算法对该优化问题进行寻优。另外由于支持向量机参数对模型预测精度有较大影响，利用改进的粒子群算法对该参数进行寻优，构建高拟合精度的支持向量机近似模型。因此，将改进粒子群优化算法与支持向量机模型相结合，对压路机驾驶室板厚进行优化，降低其驾驶室内的结构噪声。

1 SVM与PSO组合优化驾驶室结构噪声理论基础

1.1 支持向量回归机

假设训练集为{(xi,yi)，i=1,2,…n}，假设训练集数据在拟合精度为ε下利用回归函数 f(x)=ω·x+b对其拟合，式中 ω为权向量，b为偏差，ω∈Rn。考虑允许拟合误差，引入惩罚因子C、松弛因子则函数拟合问题转化为

非线性回归模型通过构造一个非线性映射Φ(x)，使得样本点在高维特征空间里是线性的，上述映射主要是通过核函数来实现。则非线性回归函数表示为

式中αi以及为拉格朗日乘子，其对应样本为支持向量，本文使用核函数为径向基函数(RBF）：

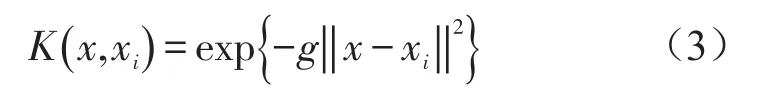
1.2 改进粒子群优化算法

粒子群算法首先在可解空间初始化一群粒子，每个粒子代表可解空间的一个可能最优解，用位置、速度、适应度值三个指标来描述粒子的基本特征。其中适应度决定解的优劣程度，一般根据优化目标定义适应度函数。假设在d维的搜索空间中有一个n个粒子组成的种群，第i个粒子在搜索空间中的位置为其速度决定它的方向和距离。整个粒子群每一次迭代粒子的速度和位置由以下方程进行变化

式中ω为惯性权重系数，c1、c2为学习因子，γ1、γ2为介于[0,1]之间的随机数。为防止粒子速度过快错过最优解，设定粒子飞行速度为-vdmin≤vi≤vdmax，搜索范围设定为-xdmin≤xi≤xdmax，pbest为粒子自身最优解的位置，gbest为整个种群的最优解。

针对粒子群可能出现局部最优解的问题，本文提出采用非线性动态改进惯性权值以及非线性动态调整学习因子对粒子群进行改进。

（1）非线性动态改进惯性权值

惯性权重起到平衡全局搜索和局部搜索能力的作用，本文提出随粒子的适应度值自动调整惯性权值，每次惯性权值ω表示为

式中ωmax、ωmin分别为惯性权值ω最大值和最小值，f为粒子当前适应度值，favg、fmin分别为当前所有粒子平均适应度值和最小适应度值。

（2）非线性动态调整学习因子

从式（7）可以看出，随着迭代不断进行学习因子在优化过程中随时间进行不同变化，增强粒子早期迭代全局搜索能力、后期迭代局部搜索能力。

式中c1,ini、c2,ini为c1和c2的初始值，c1,fin、c2,fin为c1和c2的迭代终值，t为迭代次数。

2 基于SVM与PSO的结构噪声优化流程

基于SVM和PSO组合优化驾驶室结构噪声设计流程，先建立驾驶室声固耦合模型；再进行拉丁超立方试验设计，利用有限元计算在各个样本点下驾驶室驾驶员右耳处声压响应、驾驶室设计变量总质量、一阶扭转模态频率；然后建立基于支持向量机的驾驶室结构噪声优化设计模型；最后通过改进粒子群优化算法优化驾驶室板厚设计参数，降低压路机驾驶室结构噪声。基于支持向量机和改进粒子群算法优化压路机驾驶室结构噪声基本流程如图1所示，基本步骤如下：

图1 IPSO-SVM-IPSO流程图

1）构建驾驶室声固耦合有限元模型，确定影响驾驶室结构噪声主要设计变量及其变化范围并确定驾驶室噪声主要评价标准。

2）拉丁超立方试验设计方法生成样本点，将样本点代入有限元模型计算右耳处声压响应、驾驶室设计变量总质量、1阶扭转模态频率，并将这些样本点分为训练样本和预测样本。

3）用训练样本训练支持向量机模型，同时用改进的粒子群算法对支持向量机的不敏感系数ε、惩罚因子C、核宽度g这三个主要参数进行寻优，找到最合适一组参数组合使得适应度函数最小，获取拟合精度较高的近似模型。

4）利用预测样本检测近似模型的泛化能力。

5）基于建立的支持向量机近似模型，在满足约束条件的基础上，利用改进的粒子群计算最佳板厚使目标函数最优。

6）更新板件厚度为获取最优设计量，通过有限元计算，比较优化前后效果。

3 算例分析

本文以某款正处于研发阶段的高频双钢轮压路机为研究对象，在压路机产品正向设计阶段，利用SVM和PSO组合优化驾驶室结构噪声，减少样机生产后试验次数，提高效率。

3.1 有限元模型

建立驾驶室的结构有限元模型和声腔有限元模型，并以这两个模型构建声固耦合模型（图2）。有限元模型采用壳单元和实体单元进行网格划分，顶部与驾驶室骨架、门与门框的连接在连接点处采用刚性单元RBE2模拟；操纵台及座椅与驾驶室底部的连接也采用刚性单元RBE2模拟。驾驶室声腔有限元模型采用实体单元进行划分，所有单元节点均定义为流体节点，单元材料为空气，并由空气密度及声速确定其体积模量。

图2 驾驶室声固耦合模型(隐藏玻璃）

3.2 设计变量

压路机驾驶室很多板件都具有对称性，考虑到工程要求不对压路机玻璃厚度进行改进，则本文将压路机驾驶室的主要板件分成7个变量（如图3），其取值范围如表1所示。

3.3 样本采集与预处理

为减少试验次数，提高计算效率，采用拉丁超立方试验设计生成75个有限元模型样本，其中前60组作为训练数据，后15组为预测数据。将这些样本带入到驾驶室声固耦合有限元模型中，在车身左前悬置施加20 Hz～200 Hz的垂向激励，幅值为10N。

图3 设计变量示意图

表1 设计变量取值范围

选定驾驶员右耳处为车内参考点，利用有限元软件基于模态频响理论得到参考点声压，利用公式（8）计算得到该点A计权声压级均方根值，并以此作为衡量驾驶室结构噪声重要标准即本文所设定的目标函数。然后分别计算各个样本点1阶扭转模态频率和驾驶室板件设计变量总质量（约束条件），部分样本数据如表2所示。

表2 部分样本数据（前10组）

其中Pz为均方根声压级，pi为i Hz处声压值，单位为Pa；

3.4 模型核函数参数选择

将训练样本数据带入支持向量机模型中，并用前文提到的改进粒子群优化算法对支持向量机的主要参数C、g、ε进行优化。设定C∈[0.01，1000], g∈[0.0001,10]，ε∈[0.001,0.1]，粒子群种群规模为40，迭代次数为200，c1,ini=2.5、c1,fin=0.5、c2,ini=0.5、c2,fin=2.5、ωmax=1.2、ωmin=0.6，分别构建声压级均方根值、1阶扭转模态频率、驾驶室设计变量总质量和板厚之间的支持向量机近似模型。经计算可知，三个支持向量机模型主要参数的最优值如表3所示。

表3 支持向量机主要参数值

3.5 支持向量机模型精度评价

为比较SVM预测模型的准确性，本文将SVM和工程比较常用的2阶响应面法在拟合结果上进行比较，从而证明SVM的准确性。声压级均方根值、1阶扭转频率预测样本的SVM以及RSM拟合结果与有限元计算值比较如图4、图5所示。

图4 驾驶室声压均方根预测样本拟合精度比较

图5 1阶扭转模态频率预测样本拟合精度比较

从图4、图5可以看出基于声压均方根值以及扭转频率的两种近似模型都有较好的数据泛化能力，但PSO优化的SVM比响应面近似模型对于样本点的响应更接近于有限元仿真数据。声压均方根值SVM近似模型相对于有限元仿真值的相对误差均在2%以内，而1阶扭转模态频率SVM近似模型相对于有限元仿真值的相对误差均在0.5%以内。从而证明构建的驾驶室支持向量机近似模型比响应面近似模型有更高的拟合精度，本文将利用SVM近似模型代替原来的有限元模型。

3.6 基于支持向量机近似模型优化

通过优化驾驶室板厚降低压路机车内结构噪声，且由于驾驶室结构的1阶扭转模态频率是一个很重要技术指标，是衡量车内结构在低频共振时抵抗扭转的能力。将驾驶室设计变量总质量以及1阶扭转模态频率作为约束条件，在优化过程中设定在一定变化范围内。因此使驾驶室车内结构噪声最小的数学优化模型如下：

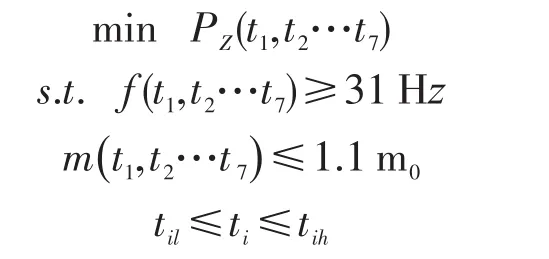
式中pz为声压级均方根值，f为1阶扭转模态频率，m为设计变量总质量，m0为设计变量总质量初始值，ti为设计变量，til、tih分别为设计变量下限和上限。

基于上述所建立SVM模型，利用改进PSO对驾驶室板厚进行寻优，使得驾驶室声压响应最小。由于PSO属于无约束优化算法，本身不能处理约束条件，本文的优化问题将通过建立惩罚函数机制将约束问题转化为无约束问题求解，优化结果如表4所示。且由于优化后的板厚参数小数点众多，而工艺很难达到，一般选取板厚变量参数小数点后一位。

从表4可知，根据实际情况最终优化的板厚与最初优化结果有所差异，导致最终优化的A计权声压级均方根值也有所区别。经计算，驾驶室声压级均方根值下降2.7 dB，1阶扭转模态频率为31.33 Hz，设计变量总质量为179.8 kg均满足约束条件要求。通过比较可知，结构噪声优化达到理想效果。

表4 设计变量以及响应优化前后对比

为更直观比较板厚改进前后对驾驶室噪声的控制效果，将有限元的模型中的板件厚度改为优化的最终值，并在车身左前悬置施加20 Hz～200 Hz的垂向激励，幅值为10 N，重新计算驾驶室右耳处声压响应值，并将其与优化前的声压响应比较如图6所示。

图6 优化前后驾驶室声压响应比较

从图6可以明显看出，按照最终取值修改驾驶室板厚，能明显降低驾驶室结构噪声，其中压路机主要工作频率处50 Hz和67 Hz以及声压级峰值频率点105 Hz、140 Hz、187 Hz处声压级分别下降1.4 dB、1.2 dB、3.1 dB、2.8 dB、9.7 dB，在整个频率范围内声压级均方根值降低2.7 dB，降噪效果显著。

4 结语

本文针对压路机驾驶室结构噪声，将试验设计、近似模型、粒子群优化算法相结合对压路机结构噪声进行优化设计，得到如下结论：

（1）本文基于SVM和PSO，以板厚为设计变量，分别构建场点A计权声压级均方根值、驾驶室设计变量总质量、1阶扭转模态频率的支持向量机近似模型，利用该模型替代有限元模型，并用改进的PSO对其进行优化计算，减少计算工作量，提高优化效率；

（2）基于PSO优化的支持向量机近似模型预测精度能较好的满足工程要求，为大型的结构优化问题提供新的解决方法。

[1]Liang Xin-hua,Lin Zhong-qin,Zhu Ping.Acoustic analysis of damping structure with response surface method[J].Applied Caustics,2007,68:1036-1053.

[2]Li Zai-wei,Liang Xin-hua.Vibro-acoustic analysis and optimization of damping structure with response method [J].Materials&Design,2007,28:1999-2007.

[3]藏献国，于德介，姚凌云.响应表面法在结构噪声优化中的应用研究[J].噪声与振动控制，2009，29(4)：116-119.

[4]高云凯，张朋，吴锦妍，等.基于Kriging模型的大客车侧翻安全性多目标优化[J].同济大学学报(自然科学版)，2012，40(12)：1882-1886.

[5]周礼辉，成艾国，陈涛.基于BP神经网络的侧碰多目标优化设计[J].中国机械工程学报，2012，23(17)：2122-2127.

[6]袁野，陈昌亚，王德禹.基于支持向量机的卫星动力学多目标优化[J].振动与冲击，2013，32(22)：189-192.

[7]姚凌云，于德介.基于支持向量机响应面的车身部件特性优化[J].湖南大学学报(自然科学版)，2008，11(35)：21-25.

[8]Li Sun,Deyu Wang.Optimal structural design of the midship of a VLCC based on the strategy integrating SVM and GA[J].Journal of Marine Science and Application, 2012,11(1):59-67.

[9]Fernandez Martinez J L,Garcia Gonzalo E,Fernandez Alvarez J P.Theoretical analysis of particle swarm trajectories through a mechanical analogy[J]. International Journal of Computational Intelligence Research,2008,4(2):93-104.

[10]向国齐，黄大贵，严志坚.支持向量机和粒子群算法在结构优化中的应用研究[J].计算机应用研究，2009，26(6)：2059-2061.

[11]张学丘，陈剑.某矿车驾驶室内结构噪声分析与控制[J].噪声与振动控制，2012，32(4)：88-91.

[12]杨楠，左言言，陈冬冬.3 t叉车驾驶室声学特性分析[J].噪声与振动控制，2012，32(5)：88-91.

Application of SVM and Improved PSO in Structure Noise Optimization for the Road Roller Cab

HE Jian-jun1,FU Ling2,3,YANG Chuan2,3,YANG Peng2,3
（1.School of Mechanical Engineering,Xiangtan University,Xiangtan 411105,Hunan China; 2.Zoomlion Heavy Industry Science and Technology Co.Ltd.,Changsha 410013,China; 3.State Key Laboratory of Key Technology of Construction Machinery,Changsha 410013,China)

The Latin hypercube experimental design,support vector machine(SVM)approximation model and improved particle swarm optimization(PSO)algorithm were combined to reduce the structure noise of a road roller’s cab by modifying the thickness parameters of the main plates of the cab.The design process for controlling the interior structure noise based on the SVM and PSO was presented.The particle swarm was improved by the PSO which could lead to a local optimal solution.The SVM model with high fitting accuracy was built and the improved particle swarm was used to optimize the plate thickness parameters of the SVM model.A set of the best parameters of the thickness that could minimize the sound pressure level at the reference point(the driver’s right ear)was found.The process could save the computation workload and improve the efficiency of the optimization.

acoustics;road roller;support vector machine;cab;structure noise

33+.1

A

10.3969/j.issn.1006-1335.2015.03.027

1006-1355(2015)03-0124-06

2014－09－28

国家863计划项目：工程机械共性部件再制造关键技术及示范(2013AA040203)

贺建军(1989－)，男，湖南岳阳人，硕士研究生，主要研究方向：工程机械NVH性能研发。E-mail:hejianjun07@126.com