基于诱发因素作用特征的滑坡变形时序模型

黄 丽，罗文强，李飞翱，刘小珊

(中国地质大学(武汉)数学与物理学院，武汉 430074)

1 研究背景

根据大量的监测资料，降雨和库水位变化对滑坡位移变形有着重要的影响。降雨和库水位变化的滞后性和周期性是滑坡变形的重要作用特征。因此在滑坡变形预测的模型中考虑诱发因素的滞后性和周期性是非常有必要的。

当前，滑坡变形预测以时序分析为主的研究逐渐增多，例如，缪海波等［1］基于非平稳时间序列分析的滑坡变形预测，用GM(1，1)模型进行趋势项提取，三角函数拟合周期项数据，应用时间序列方法所建模型效果良好;徐峰等［2］提出的基于时间序列分析的滑坡位移预测模型的研究，采用二次平移分离滑坡位移的周期项和位移项，分别采用GM(1，1)预测趋势项和AR模型预测周期项，滑坡位移曲线拟合较好，与实际位移变化趋势较一致。以上研究主要是位移与时间单变量时序模型，并未将降雨和库水位变化直接纳入滑坡变形预测模型中。石爱红和牛瑞卿［3］提出的库水位响应滞后影响下的滑坡位移预测模型研究，选取月降雨量与库水位滞后影响下的库水位平均变化量为诱发因子，采用时间序列的方法对滑坡进行了动态预测，为滑坡的动态预测提供了可靠的依据，但未能考虑到诱发因素周期性的影响。针对上述问题，本文根据诱发因素的滞后性和周期性的对滑坡变形的影响，采用多元时间序列的方法建立模型:首先用灰色模型进行提取趋势项位移，然后直接利用滞后的降雨量和滞后的库水位的变化量预测当期的周期项位移，最后建立描述诱发因素(降雨量和库水位变化)的滞后项与滑坡累积位移之间关系的多元时序模型，并对滑坡位移进行了预测。

2 滑坡位移的动态分析

在滑坡发育过程中累积位移一般呈单调递增的特征，具有明显的增长趋势，因此滑坡的监测数据序列可以看作是非平稳时间序列［3］。考虑到滑坡由于受到自身地质条件的影响会产生一个趋势项位移;受到降雨、库水位变化等外在因素的影响会产生一个周期项位移。因此可以将滑坡累积位移序列看成趋势项、周期项和随机项，即

式中:St是t时刻观测的滑坡累积位移;Xt是t时刻的趋势项;Ct是t时刻的周期项;Rt是t时刻的随机项。

2.1 趋势项提取

趋势项，即反应时间序列的发展动向。滑坡累积位移受其自身基础地质条件的影响会产生一个趋势向位移。滑坡累积位移数据为单调递增的非线性时间序列，且对研究区不同类型滑坡累计位移监测曲线进行分析后发现，各种检测曲线为近似指数增长曲线［4］，所以我们采用GM(1，1)模型提取趋势项。

GM(1，1)原理［5］如下:

原始数据序列表示为

式中:X(0)为一个非负并且相等时间间隔的序列;n为序列的个数。

当X(0)累计求和算子(AGO)，得到序列

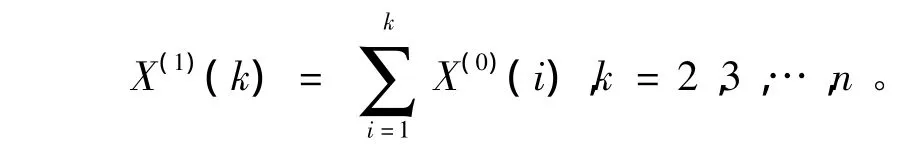
则可以通过一个一阶微分方程来构造GM(1，1)模型，即

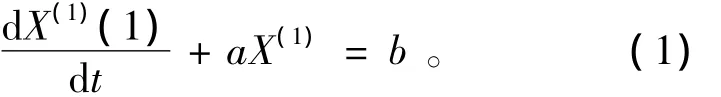
式中a和b是待定系数，可以通过最小二乘法决定，即

其中:

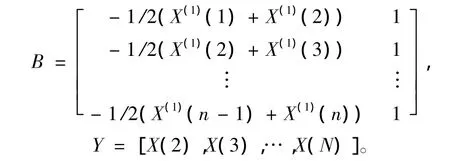
当a和b代入方程(1)中时，得到解为

将累计求和逆算子应用到上面方程中，可以得到原始数据在时刻k的预测结果，即

2.2 周期项提取

周期项，即具有一定周期性变化的序列。滑坡累积位移受到降雨、库水位变化等外在因素的影响会产生一个周期项位移。本文考虑降雨、库水位变化量的周期性和滞后性影响，直接将月平均降雨量和月库水位变化量作为影响周期项位移的影响因子，构造多元时间序列模型，即

式中:C(t)表示t月份的周期项位移;Rt表示t月份的平均降雨量;ΔK(t)表示t月份的库水位相对于(t－1)月份的库水位变化量;u为常数项;α为前一期周期项系数，βi(i=0，1，2，…，n)为滞后 i期的降雨量系数;ri(i=0，1，2，…，n)为滞后 i期的库水位变化系数。

同时考虑诱发因素的周期性和滞后性作用来进行周期项位移预测，突出了诱发因素的作用特征。将趋势项位移与周期项位移叠加得到滑坡变形位移预测的多元时序模型，更加清晰地突出了诱发因素与累积位移之间的动态变化。

3 实例应用

白水河滑坡处于三峡库区长江宽河谷地段秭归县境内，南高北低，呈阶梯状向长江展布，滑坡体为一特大型老滑坡松散堆积体，发育于秭归向斜西翼，出露地层为侏罗系下统香溪群中厚层状砂岩夹薄层状泥岩［6］。降雨及库水位变化是诱发白水河滑坡变形的主要因素，位于预警区中西部的ZG93和ZG118监测点的位移序列较好地体现了预警区滑体在降雨和库水位变动下的整体变形规律［7］。本文以监测点ZG93为代表，取其2005年1月到2006年12月的滑坡累积位移监测数据，又由于白水河滑坡为降雨与库水位联合作用型的滑坡，所以同时取2005年1月到2006年12月共24个月的月平均降雨量和2004年12月到2006年12月共25个月的月库水位监测数据。以所取得累积位移数据、降雨及库水位数据为依据，采用上述方法确定诱发因素周期和滞后响应的滑坡累积位移预测的多元时序模型。

图1为白水河滑坡2005年1月到2006年12月的累积位移数据曲线(图1(a))、降雨量数据曲线(图1(b))、2004年12月到2006年12月的月库水位数据曲线(图1(c))、2005年1月到2006年12月的月库水位变化量数据曲线(图1(d))。

从图1(a)可以看出滑坡累积位移曲线明显地呈现出非线性，单调递增性且类似指数增长的趋势，在MatLab中利用GM(1，1)模型提取趋势项，可得到

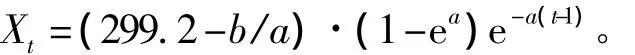
不考虑随机扰动项，利用累积位移数据减去趋势项位移得到周期项位移Ct。周期项曲线见图2。

图1 白水河滑坡监测累计位移、月平均降雨量曲线、库水位及库水位变化量与时间关系曲线Fig.1 Cumumlative displacement-time，aerage monthly rainfall-time，reservoir water level-time，and reservoir water level variation-time curves of Baishuihe landslide

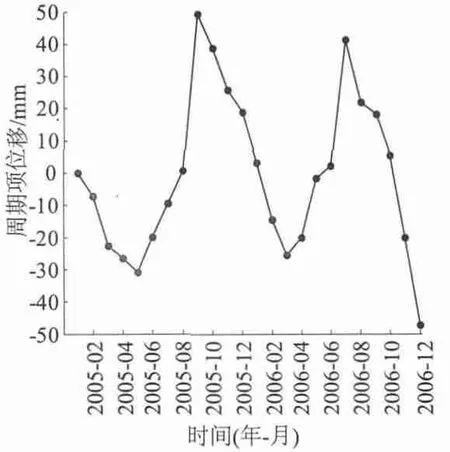
图2 白水河剔除趋势项之后的周期项曲线Fig.2 Curve of periodic term displacement vs.time of Baishuihe landslide in the absence of trend term

从图2可以看出，剔除趋势项后的数据呈现出明显的周期性，由此可以看出受内在因素影响产生的趋势项位移已基本剔除。

首先对比周期项位移与降雨量对应的图形，从整体来看，图形趋势大体一致，从细节上看当降雨量第1次达到最大值时是2005年8月，而周期项位移在2005年9月达到一个最大值;当降雨量2005年12月减小到最低值时，而周期项位移在2006年3月达到最小值;当降雨量第2次达到最大值时是2006年6月，而周期项位移第2次达到最大值时是2006年7月，显然降雨对周期项位移有滞后性影响。

其次，再对比周期项位移与库水位变化量的图形，从图上可以看出在2005年5，6月时库水位变化量下降，在6月第1次达到最小(当期库水位下降);而周期项位移曲线在2005年7—9月迅速递增(周期项位移变大)，在9月周期项位移达到第1个最大值。库水位变化量在2006年9月和10月开始上升，在10月达到最大值，而周期项位移从2006年10—12月开始迅速变小。可见，当库水位下降时，周期项位移加大;库水位上升时可抑制周期项位移上升，并且从时间上来看库水位变化量对周期项位移也有一定的滞后影响。

利用Eviews软件计算滞后项系数的显著性，从而筛选滞后项，具体步骤为:

(1)在Eviews中通过自相关系数和偏自相关系数图对周期项序列进行相关性分析，判断周期项序列的当前项与前一项是相关的。

(2)根据周期项的数据曲与降雨量曲线图和库水位变化量曲线图分析，以及公式(2)，计算得到的滞后项系数所对应的P值大小做初步的筛选。P值越大说明此项不能作为周期项位移的可靠指标，要排除;反之，则留下［8］。

根据上述方法，利用式(2)，在 Eviews的 Estimate Equation中先输入如下变量:

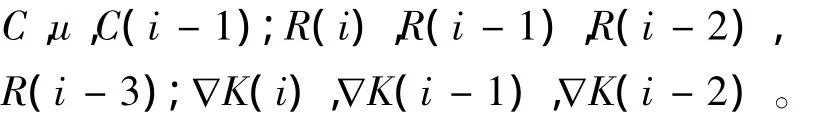
其中R(i)，R(i－3)，∇K(i)和∇K(i－2)的系数对应的P值较大(＞0.05)，所以先剔除这几项，随后在Estimate Equation中输入留下的变量C，u，C(i－1)，R(i－1)，R(i－2)，∇K(i－1)，得到相应的系数及P值，其中R(i－2)的P＞0.05，所以再剔除R(i－2)这一项，这时对应的系数且P值均＜0.05。最后得到C(t)的表达式为

然后，将趋势线和周期项叠加则有

从此模型的表达式可以看出，前1个月的月平均降雨量和前2个月的库水位变化对当前一期滑坡累积位移产生的影响，利用此模型对白水河滑坡2007年1—5月的累积位移进行预测，根据Rt=St－(Xt+Ct)算出随机误差，并分别画出滑坡累积位移实际数据与预测数据对比图(图3)和误差百分比表(表1)。

从图3可以看出，滑坡实际累积位移曲线与预测累积位移曲线基本吻合;从表1可以看出，预测误差百分比较低，说明此模型能够较好地反映诱发因素与累积位移的动态关系。

图3 白水河滑坡监测点ZG93累计位移的预测曲线与实测曲线Fig.3 Curves of predicted and measured cumulative displacement of monitoring point ZG93 of Baishuihe landslide

表1 白水河滑坡监测点ZG93累计位移的预测误差Table 1 Prediction error of the cumulative displacement of monitoring point ZG93of Baishuihe landslide

4 结论

(1)降雨、库水位变化是滑坡发生的主要外在诱发因素，降雨和库水位变化的滞后性和周期性是滑坡变形的重要作用特征。

(2)实例表明，白水河滑坡累积位移受到前一期降雨及前一期库水位变化量的影响。从模型系数可以看出，累积位移与前一期降雨成正相关，与前一期库水位变化成负相关，当前一期降雨量增大时，当期滑坡累积位移会有变大的趋势;前一期库水位下降时，当期滑坡累积位移变大;当前一期库水位上升时，当期滑坡累积位移变化较小。

(3)同时考虑降雨及库水位变化量的滞后性和周期性影响提高了预测的精度，平均绝对误差为1.97%，反映了滑坡位移与诱发因素之间的动态关系。

［1］缪海波，殷坤龙，柴 波，等.基于非平稳时间序列分析的滑坡变形预测［J］.地质科技情报，2009，28(4):107－111.(MIAO Hai-bo，YIN Kun-long，CHAI Bo，et al.Deformation Prediction of Landslide Based on the Analysis of Non-stationary Time Series［J］.Geological Science and Technology Information，2009，28(4):107－ 111.(in Chinese))

［2］徐 峰，汪 洋，杜 娟，等.基于时间序列分析的滑坡位移预测模型研究［J］.岩石力学与工程学报，2011，30(4):746－751.(XU Feng，WANG Yang，DU Juan，et al.Study of Displacement Prediction Model of Landslide Based on Time Series Analysis［J］.Chinese Journal of Rock Mechanics and Engineering，2011，30(4):746－751.(in Chinese))

［3］石爱红，牛瑞卿.库水位影响下的滑坡位移预测模型的研究［J］.安全与环境工程，2013，20(1):26－29.(SHI Ai-hong，NIU Rui-qing.Research on the Displacement Prediction Model of Landslide under the Influence of the Response Hysteresis of Reservoir Water Level［J］.Safety and Environmental Engineering，2013，20(1):26－29.(in Chinese))

［4］杜 娟，殷坤龙，柴 波.基于诱发因素响应分析的滑坡位移预测模型的研究［J］.岩石力学与工程学报，2009，20(9):1783－ 1789.(DU Juan，YIN Kun-long，CHAI Bo.Study of Displacement Prediction Model of Landslide Based on Response Analysis of Inducing Factors［J］.Chinese Journal of Rock Mechanics and Engineering，2009，20(9):1783－1789.(in Chinese))

［5］LI Xiu-zhen，KONG Ji-ming，WANG Zhen-yu.Landslide Displacement Prediction Based on Combining Method with Optimal Weight［J］.Nature Hazard，2012，30(4):746－751.

［6］王尚庆，徐进军，罗 勉.三峡库区白水河滑坡险情预警方法研究［J］.武汉大学学报，2009，34(10):1218－1221.(WANG Shang-qing，XU Jin-jun，LUO Mian.Study on Warning of Dangerous State of Baishuihe Landslide in Three Gorges Reservoir Area［J］.Geomatics and Information Science of Wuhan University，2009，34(10):1218－1221.(in Chinese))

［7］李远耀，殷坤龙.三峡库区渐进式库岸滑坡的预测预报研究［D］.武汉:中国地质大学，2010.(LI Yuan-yao，YIN Kun-long.Research on Prediction and Forecast of Progressive Bank Landslide in the Three Gorges Reservoir［D］.Wuhan:China University of Geosciences，2010.(in Chinese))

［8］高铁梅，王金明，梁云芳，等.计量经济分析方法与建模Eviews应用及实例(第二版)［M］.北京:清华大学出版社，2009.(GAO Tie-mei，WANG Jin-ming，LIANG Yun-fang，et al.Econometric Analysis Method and Model:Eviews Application and Examples(Second Edition)［M］.Beijing:Tsinghua University Press，2009.(in Chinese))