舰船电力系统暂态稳定性研究

李文才，郝国芬

(河北工程技术高等专科学校，河北 沧州061001)

0 引 言

船舰系统的设计构造复杂，其中使用的越来越精密的装置设备，需要一个较为完善高效的电力系统支撑。在电力系统潜在的各种问题中，其发电机进行持续稳定的供电问题即其暂态稳定性能，对于舰船整体安全有效的运行起着重要作用。对电力系统安全有效的检测需要用到暂态稳定分析研究，分析的方法及结果是影响系统判断的重要手段。在电力系统研究领域中，船用电力系统研究尚处于起步阶段，较多问题亟待解决，而陆用电网的发展已经日趋成熟，有丰富的经验可供参考。舰船电网涉及繁杂精密的电子设备，且回路复杂，所以对其暂态稳定的研究具有一定的难度。

舰船电网的暂态稳定性研究牵涉因素复杂，需考虑问题众多。本文首先提出了一个放电机组全方位数学模型，包括发电机、励磁原理、调速、负荷模型;接着通过对电力系统发电机工作的分析，采用合适的算法实现舰船电力系统的暂态稳定性模拟仿真，并对仿真结果与舰船实际工作状态进行客观比较，验证该算法方案的可行性和应用的价值。

1 数学模型

电力系统的构成主要可分为2个部分，一部分主要由发电机及传输设备构成，为系统提供能量，另一部分包括励磁器、调速器等，主要负担起调节电网工作状态的功能。

1.1 同步发电机模型

对发电机工作情况转化为如下方程:

上式中:E′q，ω，δ 分别为电压电势，功角速度及功角;现假设发电机初始电压为:

在运行中状态暂态电压与励磁力矩分别为

对各扰动因素用D，Q 坐标下的等效阻尼D(ω-1)表示，则励磁力矩为:

1.2 励磁模型

励磁系统主要作用是调控电压，以基本的比例式模型为基础，调节过程如图1所示。

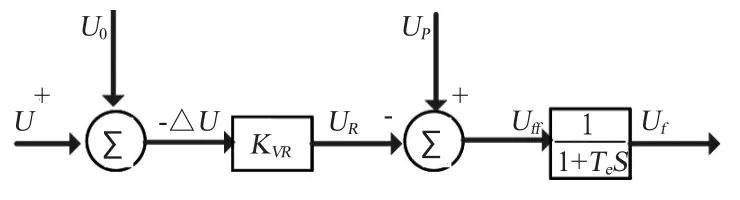
图1 励磁系统Fig.1 Excitation system

由图1 可得系统状态方程:

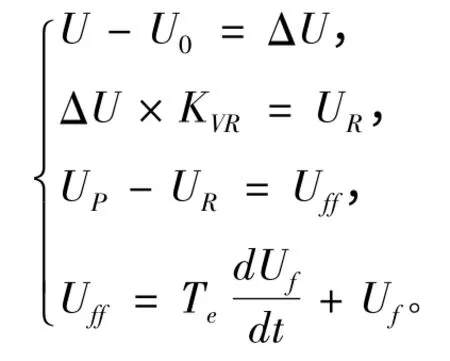
由系统状态稳定时的电压关系知:

将Up代入则系统状态方程在电压扰动影响下的偏差:

若发电机在运行中无负载的电压增量计为:

则电压扰动偏差的关系可表示为:

其中:Kv=XadKvr/Rf，Kv为放大系数。

1.3 调速模型

调速器工作主要任务是进行功率调节，转换方式如图2所示。

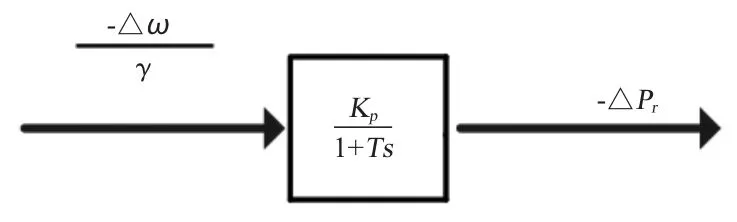
图2 调速器框图Fig.2 Governor principle

功率控制通过过程可用如下公式描述:

由系统已知的转速差与速率之比，可以算出功率增量。

1.4 负荷模型

转子负荷参与暂稳态研究时，对分析精度要求更高，则其在感应电机中状态公式如下:

其中:X′=Xm+ Xi。

2 暂态稳定性分析

2.1 系统分析原理

2.1.1 发电机节点的处理

电力系统的暂态稳定性主要根据系统运行中发电机节点和负荷状态节点的在受到扰动影响下其稳定状态的转变，由于在复杂的电力系统中，节点多且各个位置的状态计算复杂，在根据工作模型处理时需要选取合适而有效的算法来模拟仿真，为方便分析，现对发电机和负载节点处做适当处理。

假设发电机模型的定子方程为:

其导纳矩阵为:

由于迭代方法在处理非线性电路节点时具有分析优势，故本文使用迭代法处理发电机节点模型，对定子方程使用T 变换

得:

2.1.2 负荷节点的处理

考虑将负荷加入电网时的暂稳状态方程可表示为:

其中:X′为负荷暂态电抗;rs为电机感应电阻;KH为折算系数，在方程处理为电流源形式则经过变换后方程为:

2.2 分析算法及流程

以往求解节点时使用传统的欧拉算法，利用区间前端时间导数计算，使得准确度较低。当欧拉算法中对区间导数的取值通过时间步长区间两端导数均值求得时，结果的准确性提高，方法如下:

接着通过求平均取得末端精确值:

在发电机仿真中求解算法导数均值时，发电机仿真模拟可以简化为其转子状态公式:

因此有

从而发电机的功角速度ω 及功角δ 为:

则在发电机运行中第J个负荷转子方程为:

则tn时刻可表示为:

其中:

则在tn+1时刻。

由此逐渐迭代功角速度ω 及功角δ，之后对结果进行修正，其中ω 与δ 修正公式为:

Sn+1的修正公式为:

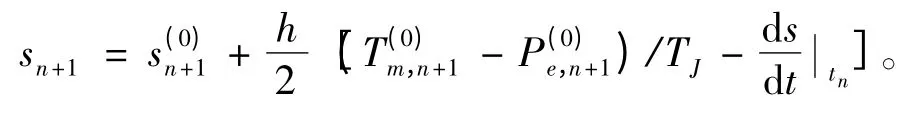
最后用同样方式算出各个时刻修正值，系统状态求解方式完成，其算法过程流程总结如图3所示。

3 仿真分析

在本文中，舰船电力系统各个节点中的在运行中主要参数状态分别如表1～表3所示。

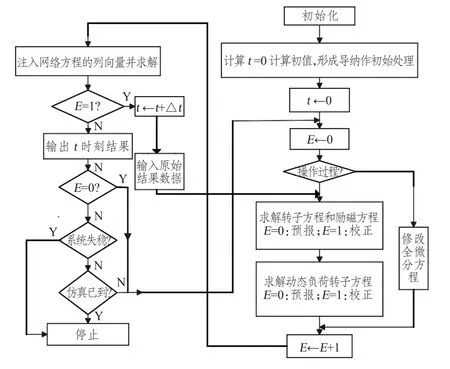
图3 改进欧拉算法分析流程图Fig.3 Improved euler algorithm analysis flow chart

表1 各组发电机参数Tab.1 Generator parameter

表2 电路各阻抗参数Tab.2 Circuit impedance parameters

表3 负载参数Tab.3 Load parameters

为了保证在电力系统暂态分析中模型的可靠，需要选择精确的仿真算法并对分析结果进行判断，本文在模拟仿真时是基于各设备点工作状态下进行的，在分析中，选取的直流发电机初始值为:

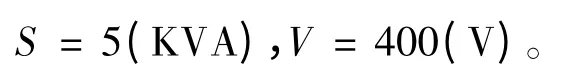
在电机转子运行中，设置其速度放大倍数Kp为3.5 倍，时间常数T=0.01，在电力系统运行状态下，瞬间在原有状态下挂载和卸载负荷时的攻角仿真状态曲线及实际状态下功角运行曲线如图4～图7所示。

图4 负荷加入仿真情况Fig.4 Load in the simulation

图5 负荷加入实际情况Fig.5 Load in actual situation

图6 负荷卸载仿真情况Fig.6 Load discharge simulation

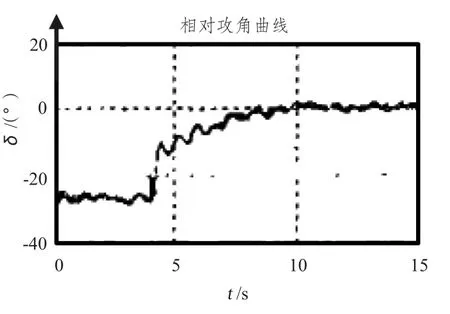
图7 负荷卸载实际情况Fig.7 Load unload the actual situation

由上述仿真状态曲线及实际状态曲线可以看出，当电路系统中突然加入一个大功率负荷时，系统功角突然改变，导致不稳定状态，在恢复稳定前，电网需经历较长时间的震荡衰减，且恢复的功角根据系统各配置不同而改变。由于仿真无法对各个电子器件进行模型状态梳理，可以看出功角仿真曲线中电力系统的暂态变化较为平滑，实际中状态过程震荡往复，但最终震荡曲线趋于稳定，即舰船电力系统的功率也调节稳定，满足系统的负载需求，保证舰船的稳定。同时，由于现实电网系统的复杂，需要将更多更详细的参数输入仿真。本文提出的仿真运行状态在一定程度上达到了与实际电力运行状态的一致性，也证明了该仿真方案的可行性。

4 结 语

随着舰船配置功能的升级优化，其电力系统稳定性要求也随之升高。本文根据陆地电网成熟稳定监测系统，提出了一种基于舰船电力系统数学模型的运行仿真分析方法，并选取合适的仿真算法，以电力系统的时域分析为基础，对其暂态稳定性进行分析，并在分析中与实际情况进行比较验证，运行结果显示仿真功角曲线和实际运行的状态相符，因此，该仿真分析方法可使用于实际舰船稳定性监测。

［1］罗伟，孙朝晖，方斌.船舶综合电力系统研究的新进展［J］.舰船科学技术，2009，31(12):105－109.

［2］肖杨婷，赵跃平，曹爽.国内外综合电力系统技术研究动态［J］.舰船科学技术，2010，32(8):24－29.

［3］柳虎.舰船电力系统微机保护与监测系统研究［D］.华中科技大学，2007.

［4］余建星，杜尊峰，温晶晶.舰船电力系统状态评估方法研究［J］.舰船工程，2008，30(6):30－41.

［5］ELDERS I M，NORMAN P J，SCHUDDEBEURS J D，et al.Modelling and analysis of electro-mechanical interactions between prime-mover and load in a marine IFEP systemf［J］.Electric Ship Technologies Symposium，2007:77－84.

［6］刘雨，郭晨，孙建波，等.舰船电力系统的动态过程仿真研究［J］.系统仿真学报，2009，21(9):2791－2795.

［7］刘水平，刘明波，谢敏.基于轨迹灵敏度的电力系统模型预测切负荷控制方法［J］.中国电机工程学报，2010，30(34):28－35.

［8］赵云利.舰船综合全电力推进系统计算机仿真研究［D］.哈尔滨:哈尔滨工程大学，2007:8－20.

［9］徐滨海.船舶电力仿真系统建模及拓扑分析［D］.哈尔滨:哈尔滨工程大学，2010，1.