混合齿轮行星系分插机构的设计与仿真

张 凯， 陶 冶， 高 宽， 林惠洲

(华南农业大学工程学院，广东 广州 510642)

混合齿轮行星系分插机构的设计与仿真

张 凯， 陶 冶， 高 宽， 林惠洲

(华南农业大学工程学院，广东 广州 510642)

将偏心齿轮-非圆齿轮行星系应用于插秧机分插机构中，研制出混合齿轮行星系分插机构。建立偏心齿轮与非圆齿轮的节曲线数学模型，获取齿轮节曲线方程，并结合KISSSOFT和MATLAB软件对非圆齿轮进行设计。建立分插机构运动数学模型，利用MATLAB开发优化辅助软件，对分插机构的参数进行优化。完成了分插机构的三维CAD设计，并在ADAMS中对分插机构进行了运动学虚拟仿真，获取了秧针尖点的静态轨迹和动态轨迹，将其与理论分析得到的轨迹曲线进行对比，验证了混合齿轮行星系应用于插秧机分插机构上的可行性。

分插机构；非圆齿轮；行星轮系；设计；仿真

非圆齿轮传动机构是一种变传动比的齿轮机构，两齿轮的节曲线是非圆曲线。非圆齿轮具有比连杆、凸轮等机构位置紧凑、刚性好、传动平稳的特点，能够在不附加其他装置的情况下精确实现变传动比运动。因此，非圆齿轮传动广泛应用于印刷、纺织、农业机械、包装、仪器仪表等领域[1]。

分插机构是高速插秧机的核心部件，市场现

有流行的分插机构是由非圆齿轮、正圆齿轮等组合而成，充分利用了非圆齿轮传动能够实现变传动比运动特性，从而设计出符合插秧农艺要求的秧针轨迹[2-3]。

非圆齿轮的设计与加工制造不同于普通正圆齿轮，其齿廓曲线需经复杂的数学模型推导，并自主开发齿廓软件设计而成；加工制造主要采用线切割方法，其制造成本较高且工序较复杂。在满足插秧农艺要求的前提下，减少非圆齿轮在分插机构传动系统中的应用可以有效地控制分插机构的设计及制造成本。分插机构零部件各项参数对秧针轨迹有很大影响，为便于后期机构的优化，开发参数优化工具是必要的。

本文介绍一种由1个非圆齿轮和2个全等正圆齿轮、1个偏心正圆齿轮组成的混合齿轮行星系分插机构。偏心正圆齿轮的齿廓与全等正圆齿轮的齿廓是一样的，所以其齿廓加工与常规齿轮加工一样。该机构采用偏心-非圆齿轮行星系减少了对非圆齿轮的使用，机构传动平稳，适用于步行式插秧机，能够实现秧针尖点的静轨迹为“海豚形”，其动轨迹形成的插秧穴口较小，可避免倒秧、漂秧的现象，符合插秧的农艺要求。对该机构进行了运动学建模，利用MATLAB开发了分插机构的参数优化工具，并在ADAMS仿真软件中进行运动学仿真，将数学模型理论分析的结果与仿真分析的结果进行对比验证。

1 非圆齿轮设计

非圆齿轮设计的第一步是节曲线的设计，包括：①按要求的传动比函数和中心距计算节曲线；②按要求再现的函数和中心距计算节曲线；③按要求符合主动齿轮节曲线方程和中心距计算从动轮节曲线[4]。3种设计方法的共同点在于都要求中心距为已知条件，然后根据另一已知量去设计非圆齿轮的节曲线方程。本文将按照第三种方法设计偏心圆-非圆齿轮传动机构，原因有：①在设计前期并不知道机构需要怎样的传动比以及非圆齿轮的运动曲线；②两轮的节曲线向径之和等于中心距，如主动轮的节曲线方程和两轮的中心距已知，则求解从动轮的节曲线方程比前两种方法简单。

如图1所示，两齿轮中心距为a，给定主动轮1的节曲线是一偏心圆，其半径为R，偏心距为e，其回转中心为O1。从动轮2为其共轭的非圆齿轮。

图1 偏心圆-非圆齿轮节曲线

某时刻位置，主动轮1的瞬时角速度为W1，从动轮2的瞬时角速度为W2，两轮转过角度分别为 φ1、 φ2。Q点为主动轮和从动轮节曲线的啮合点。初始时刻时， φ1= φ2=0。r1、r2分别为两齿轮节曲线的曲率半径，建立直角坐标系 XOY，可得偏心圆节曲线方程[5]：

i12为齿轮传动比：

r1以2π为一个变化周期，为了满足齿轮单向连续性传动，以传递周期性的运动关系，要求从动轮节曲线是封闭的，偏心圆齿轮转角φ1在0～2π变化时，从动轮转角 φ2也在0～2π变化，所以：

由式(3)～(4)可解出中心距a值；求得从动轮的节曲线方程为：

2 混合齿轮行星系分插机构设计

2.1 结构及工作原理

混合齿轮行星系分插机构由 2个全等正圆齿轮、1个偏心正圆齿轮和1个与其共轭的非圆齿轮组成，如图2所示。偏心正圆齿轮2固定不动，非圆齿轮 3与其啮合，正圆齿轮4与非圆齿轮3固定在同一根转动轴上，正圆齿轮5和正圆齿轮4啮合。其中O1、O2、O3分别为偏心正圆齿轮2、

非圆齿轮3、正圆齿轮5的转动中心。

工作时行星架1在中心轴的带动下，使齿轮2与齿轮 3啮合，引起传动比的变化，从而导致行星圆齿轮 5作往复摆动。栽植臂 6和行星圆齿5固联，它一方面随着行星架作圆周运动，另一方面随着行星圆齿轮作往复摆动，形成秧爪要求的运动轨迹和姿态。

图2 混合齿轮行星系分插机构示意图

2.2 秧针轨迹数学模型

建立XOY坐标系，如图2所示，可得秧针尖点E的轨迹方程：

E点静轨迹相对位移方程：

E点动轨迹绝对位移方程：

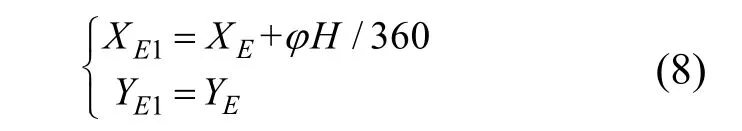
式中，φ0为行星的初始安装角度(φ0＞0)；φ为某一时刻行星架转过得角度(φ＜0)；δ0为方向轴 O1O2与O2O3之间的夹角；φ52为行星轮5相对中心轮2的转角；α0与O3E与O1O2之间的夹角；H为秧苗株距；S为行星轮5中心O3到秧针尖点E之间的距离。

2.3 参数优化与优化目标

为获得满足插秧农艺要求的插秧轨迹，需对秧针尖点 E轨迹方程中的各项参数进行优化，即求得一组最佳参数，使得轨迹满足要求。根据2.2的轨迹数学模型，基于MATLAB开发了分插机构参数优化工具，该工具的人机交互界面如图 3所示。软件界面包括：参数输入区、图形显示区、数据结果区、以及清除退出空间。

通过MATLAB软件的图像生成技术实时显示秧针的相对运动轨迹和绝对运动轨迹，能够使设计者快速判断出插秧轨迹是否满足插秧要求，并得到合适的机构参数。

图3 分插机构参数优化软件界面

具体优化目标如下[6-9]：

(1) 取秧角(秧针取秧时与水平线的夹角)应在–10°～20°之间，而推秧角(秧针推秧时与水平线的夹角)应在65°～80°之间；

(2) 绝对运动轨迹的地面穴口宽度小于30 mm；

(3) 秧针达到最低点之前完成推秧动作；

(4) 秧针尖点轨迹要符合“海豚形”。

参数优化变量包括：偏心正圆齿轮半径R、正圆齿轮偏心距e、行星架初始安装角度φ0、方向轴O1O2与O2O3之间的夹角δ0、O3E与O1O2之间夹角α0、栽植臂参数S，通过调整参数变量，得到一组满足上述优化目标的结构参数。

2.4 优化结果

秧针轨迹方程中各项参数的变化对轨迹最终形态都有一定的影响。在满足齿轮强度的条件下，选取偏心圆齿轮半径R=20.25 mm，S=155 mm，通过改变其他参数大小调整秧针静态轨迹。需要改变的参数有4个，将其分为4组，且每一组中给定将要改变参数的 3个因素水平，分析其对秧针静态轨迹的影响，见表1。

其中，4组中各有一项参数空白，这项参数就是需要改变的参数，调整其大小，分析其对轨迹的影响。图 4所示为调整各项参数后秧针静态轨

迹的变化。

表1 混合齿轮行星系分插机构参数

由图4可知：当其他参数不变时，e或δ0值增大，轨迹越逼近“海豚形”；当其他参数不变时，φ0或 α0值减小，轨迹越逼近“海豚形”。根据优化目标，综合考虑各项参数对秧针轨迹的影响，利用参数优化软件得到一组参数：R=20.25，e=6，δ0=118，φ0=27，α0=-35，H=120，S=155，在该组参数的设定下，达到优化目标，其中取秧角为16.694°，推秧角为67.397°，插秧穴口小于30 mm。

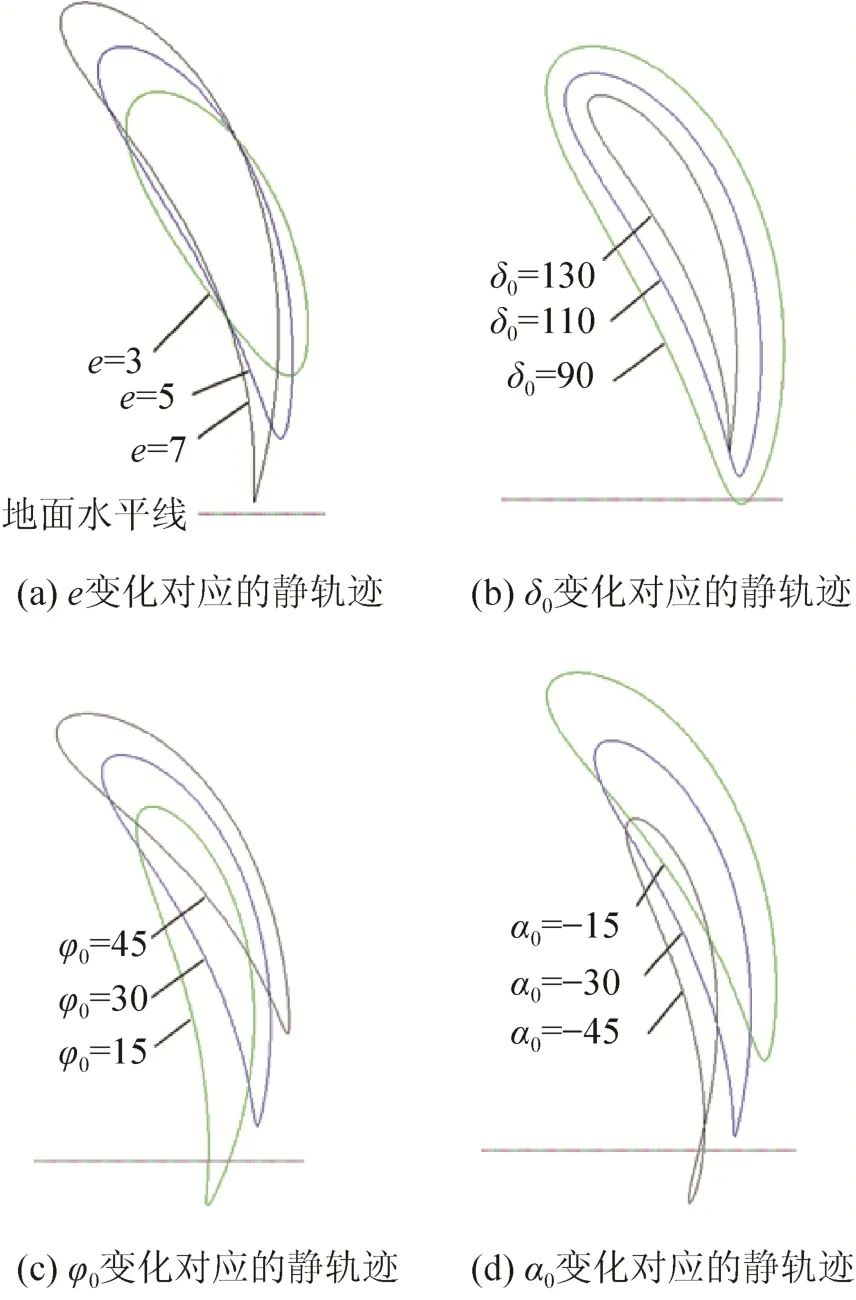
图4 静态秧针轨迹变化

3 虚拟样机建模与仿真分析

根据分插机构参数优化软件得到的各项优化参数，对分插机构的各个零部件进行建模，并装配进行运动仿真。

3.1 非圆齿轮建模

非圆齿轮由于其节曲线及齿廓设计计算复杂、三维造型及加工制造困难，应用不普及，所以能否实现非圆齿轮的快速造型成为影响其发展与应用的关键[10]。

非圆齿轮的节曲线是非圆形状，不能按照一般的设计方法在三维CAD软件设计生成。本文按照上述非圆齿轮设计中的节曲线方程，利用MATLAB软件图像生成技术，生成非圆齿轮的节曲线图形；然后提取所求节曲线的数据导入KissSoft软件中，设置齿轮其他参数，自动生成非圆齿轮的齿廓曲线；最后导入三维CAD软件生成非圆齿轮的实体，并检验运动过程有无干涉现象。同时编写了节曲线生成的人机交互界面，便于后期生成不同参数的齿轮节曲线图形。非圆齿轮的三维造型生成过程如图5所示。

图5 非圆齿轮三维CAD的生成过程图

3.2 分插机构建模与仿真

利用 SolidWorks软件对分插机构的其他零部件建模，包括行星架、栽植臂、正圆齿轮、凸轮、推秧杆等，并进行装配设计，最后保存为Parasolid格式，导入机械动力学仿真软件ADAMS中，对分插机构做运动学分析[11]，跟踪秧针尖轨迹，提取秧针尖的静态轨迹和插秧时的动态轨迹，如图6所示。

在ADAMS软件中，为机构各个零部件之间添加运动副约束关系，其中偏心正圆齿轮与非圆齿轮之间添加碰撞副。

3.3 分析与比较

为了验证秧针尖点运动轨迹数学模型的正确性，对MATLAB生成的轨迹和ADAMS运动学分析得到的轨迹进行比较。如图7所示，由ADAMS运动仿真和理论分析分别得到的秧针尖点X、Y位移曲线。对比仿真曲线与理论分析得到的曲线，可知结果基本一致。

为了验证该分插机构的传动平稳性以及秧针尖点的速度变化是否符合插秧过程农艺要求，对机构秧针尖点仿真得到的速度曲线进行了分析，如图8所示。

图6 ADAMS运动仿真秧针轨迹

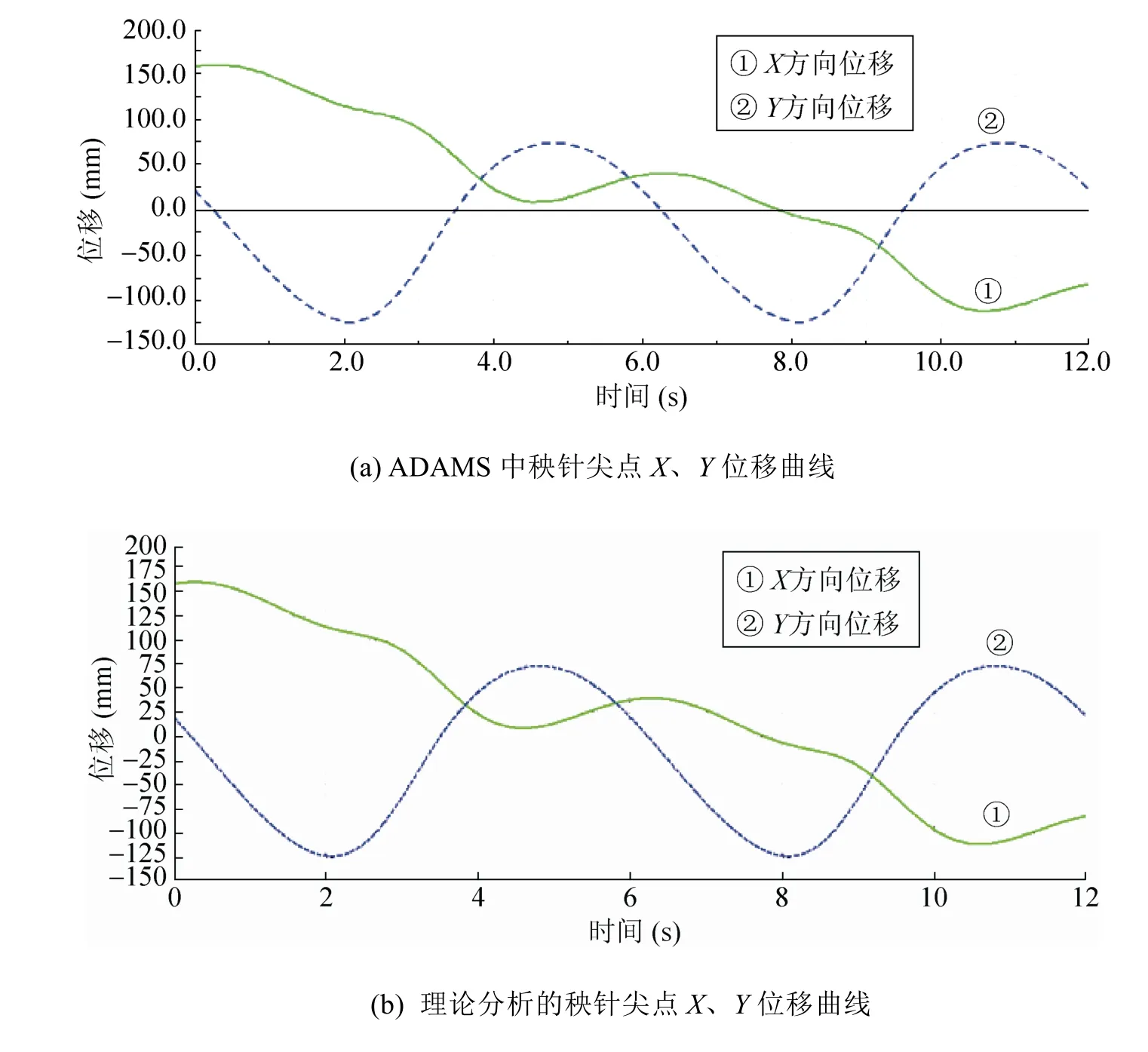
图7 仿真与理论分析尖点X、Y位移曲线

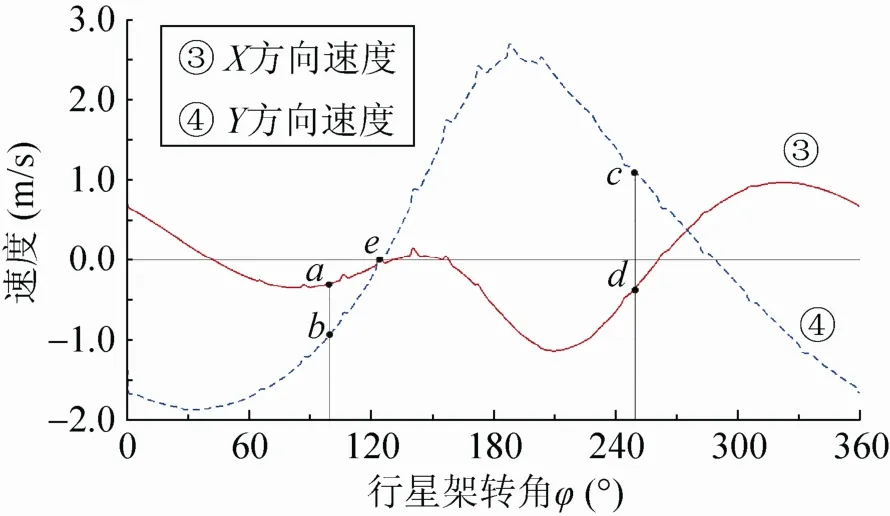
图8 仿真分析秧针尖点X、Y速度曲线

栽植臂从初始位置转到推秧位置时(速度X)曲线对应的a点，速度Y曲线对应的b点)，行星架转过100°，该过程为送秧过程，要求秧针尖点的Y方向速度较大，增大惯性，有助于插秧，该过程的Y向速度最大值达到VY=-1.86 m/s；行星架转过123°时(速度曲线X、曲线Y、X轴的交点e)，此时秧针运动至最低点，X、Y向速度为零，完成推秧过程；推秧结束后，栽植臂迅速返程，该过程 Y向速度最大值为VY= 2.7 m/s；取秧位置时(速度X曲线对应的d点，速度Y曲线对应的c点)，该位置处于Y向速度减小、X向速度增大阶段区域，可减轻对秧块竖直方向的撕扯。

该速度曲线符合插秧农艺要求：取秧要慢，竖直方向速度应减小，从而减轻对秧块的撕扯；送秧到推秧过程，要求栽植臂在竖直方向有较大的速度，迅速完成推秧动作；推秧完成后，栽植臂迅速返程。从整个速度曲线可以看出，秧针尖点的速度在X、Y方向都没有急剧增大或减小或间断跳跃，始终保持一个连续性平缓状态，说明该机构传动过程较平稳。

图 7中的对比曲线出现稍许不吻合情况以及图 8中速度曲线出现跳动的“小三角形状”的原因是：在 ADAMS运动学仿真过程中，对中心正圆齿轮和非圆齿轮之间施加的约束副为碰撞副，由于碰撞副在理论运动关系中相当于齿轮副，但是仿真过程中还是会产生一定的“失真”现象。

4 结 论

(1) 设计了一种应用于步行式插秧机上的混合齿轮行星系分插机构，其传动系统由正圆齿轮和非圆齿轮组成。与市场现有分插机构相比，该分插机构减少了非圆齿轮的使用数量，减少数量为 1～2个。在齿轮行星系设计和应用方面，实现了分插机构的结构创新。

(2) 采用了一种新的方式设计非圆齿轮，利用KissSoft和MATLAB联合设计非圆齿轮的齿廓曲线，快速得到非圆齿轮实体造型，实现了非圆齿轮设计的方法创新。

(3) 利用计算机软件开发了分插机构参数优化辅助工具，便于对机构参数的优化。对分插机构进行运动学虚拟样机仿真，将仿真结果与理论结果进行分析对比、验证，为后期分插机构的动力学分析做铺垫，同时也为分插机构的创新优化设计提供思路。

[1] 吴序堂, 王贵海. 非圆齿轮及非匀速比传动[M]. 北京：机械工业出版社, 1997： 8-22.

[2] Bae K Y, Yang Y S. Design of a non-circular planetary-gear train system to generate an optimal trajectory in a rice transplanter [J]. Journal of Engineering Design, 2007, 18(4)： 361-372.

[3] Guo L S, Zhang W J. Kinematic analysis of a rice transplanting mechanism with eccentric planetary gear trains [J]. Mechanism and Machine Theory, 2001, 36(11-12)： 1175-1188.

[4] 周 娜, 何 丽, 许纪倩. 基于MATLAB的非圆齿轮节曲线设计[J]. 机电产品开发与创新, 2007, 20(1)： 7-8.

[5] 范素香, 齐新华, 侯书林. 基于Matlab及UG的偏心共轭非圆齿轮的设计[J]. 机械传动, 2011, 35(9)： 70-72, 76.

[6] 徐洪广, 赵 匀, 张允慧, 等. 圆柱凸轮滑移式宽窄行分插机构运动学机理分析[J]. 浙江理工大学学报, 2012, 29(4)： 532-537.

[7] 赵 匀, 黄巨明, 张国凤, 等. 变形椭圆齿轮分插机构运动分析与优化[J]. 农业机械学报, 2011, 42(4)： 48-52, 61.

[8] 张 敏, 周长省, 吴崇友, 等. 椭圆齿轮行星系分插机构运动轨迹分析与仿真[J]. 农机化研究, 2011, (1)：92-94, 99.

[9] 刘天祥，杨 丽，范武君，等. 基于MATLAB插秧机分插机构秧针运动轨迹分析[J]. 黑龙江八一农垦大学学报, 2006, 18(6)： 47-49.

[10] 高雪强, 石建玲, 崔振勇. 三维环境下高阶椭圆齿轮副的运动仿真[J]. 工程图学学报, 2010, 31(4)： 104-108.

[11] 田 林, 徐世杰. 谐波齿轮几何模型参数优化及ADAMS仿真研究[J]. 工程图学学报, 2011, 32(6)：57-61.

Design and Simulation of Transplanting Mechanism with Planetary Spur Gears and Non-Circular Gear

Zhang Kai, Tao Ye, Gao Kuan, Lin Huizhou
(Department of Engineering, South China Agricultural University, Guangzhou Guangdong 510642, China)

Transplanting mechanism with planetary spur gears and non-circular gear was developed, in which planetary gear train with eccentric gears and non-circular gear is used. The mathematical model of eccentric gear and non-circular gear′s pitch curve was established and the gear pitch curve equation was obtained. Combining the KISSSOFT with MATLAB software to design the non-circular gear, kinematic models of the transplanting mechanism are established, and optimized the parameters of the mechanism by using self-compiled packages based on MATLAB. Virtual prototype simulation in ADAMS was performed after finishing the 2D and 3D design of the transplanting mechanism. The static trajectory and dynamic trajectory of the needle tip are obtained, and compared these with those of theoretical analysis. The results verify the feasibility of transplanting mechanism with planetary spur gears and non-circular gear which was applied on transplanter.

transplanting mechanism; non-circular gear; planetary spur gears; design; simulation

TH 122

A

2095-302X(2015)04-0609-06

2014-10-21；定稿日期：2014-11-24

广东省自然科学基金资助项目(S2012020010997)；公益性行业(农业)科研专项资助项目(201203059)；现代农业产业技术体系建设专项资金资助项目(CARS-01-33)

张 凯(1989–)，男，湖北黄冈人，硕士研究生。主要研究方向为机构设计。E-mail：zkyxy@stu.scau.edu.cn

陶 冶(1961–)，男，安徽安庆人，教授，硕士，硕士生导师。主要研究方向为农业种植机械及非圆齿轮研究。E-mail：taoye@scau.edu.cn