考虑拆卸序列和随机故障的机会维护策略

黄开敏，王 华，周晓军

（上海交通大学 工业工程与管理系，上海 200240）

0 引言

机会维护是一种为适应愈发复杂的多部件系统而提出的系统维护策略，ZHOU 等［1］研究了多设备串行系统的多目标机会维护策略；DING 等［2］研究了基于多级维护阈值的机会维护策略。此类维护策略一般以系统可靠性或可用度为中心，以合并维护作业的方式控制停机、拆卸等带来的成本，从经济性着手为现代企业优化维护计划并降低维护成本。

考虑到系统的结构日趋复杂，对于维修用时有严格要求或维修时拆卸较复杂的多部件系统，不应被忽略的拆卸成本和拆卸时间将使得拆卸成为多部件系统维护时必须考虑在内的因素之一［3］。目前，针对必须分步拆卸后才能维修的多部件系统的机会维护策略的需求逐步增长［4-5］，而较少有文献同时涉及拆卸规划与设备维护策略，一般的维护策略研究往往对拆卸成本做了忽略或简化［6-7］。当涉及随机故障时，以往通常使用故障率函数的期望均值来近似随机故障维护的成本，而非在仿真环境下以服从故障率函数随机发生的随机故障来动态规划维护方案［8］。正是由于随机故障带来的建模复杂性，以往研究一般都会忽略系统部件随机故障维护时其他部件实施机会维护的可能性［9］，事实上，随机发生的部件故障会涉及系统的停机和部件的拆卸问题，也将为其他部件带来维护的机会。

本文拓展了系统拆卸和机会维护时机等因素，在仿真中模拟随机故障的发生，综合考虑随机故障或预防维护时的机会维护可能，通过构建表达系统拆卸结构的拆卸树并运用拆卸序列规划获取拆卸成本，建立基于时间阈值策略的多部件系统机会维护模型，并利用Monte Carlo分析方法得到系统的优化机会维护时间阈值。

1 问题描述

本文的研究对象是包含拆卸结构的多部件复杂系统，该系统在维护时不仅具有一般的维修特性，还具有需要拆卸规划的特点。

对于部件的维护做如下假定：

（1）系统各部件为串联逻辑，当维护发生时系统需要整体停机。

（2）主要的维护活动类型包括随机故障维护、预防维护和机会维护3类。对预防维护和机会维护采用非退化的假设，认为是使部件回到全新状态的完全维护；对随机故障维护采用不改善故障率的单纯故障修复的假设。

（3）基本的维护策略有三条：①当任意部件因随机故障维护或预防维护而导致系统停机时，对系统施行指向该部件的最短路径拆卸作业后对该部件进行维护；②基于考虑拆卸成本的多部件系统的预防维护决策算法，制订各部件的预防维护计划，当部件的可靠性降低至一定程度后需预防维护以减少故障频次和故障损失；③当停机进行随机故障维护或预防维护时，考虑此时无维护活动的其余部件提前维护可能带来的收益，根据阈值策略决定其机会维护与否。

对于部件的拆卸，假定拆卸结构以一棵叉树的形式表达，拆卸过程必须满足拆卸结构约束并按树形结构逐层向下开展。通过树形遍历算法，可以找出通往特定部件的最优拆卸路径，并能够沿拆卸路径计算拆卸成本和拆卸时间。

2 多部件系统的拆卸建模

2.1 拆卸树模型

部件间的联接一般为树型、环状或网状的结构，其中树型结构因其无环有向的特点而具有典型性。Kuo［10］和Lambert［11］在拆卸序列规划研究中构 建了N叉拆卸树，作为基本的拆卸模型；高地广［12］应用结合拆卸信息表的N叉拆卸树，指出该模型在设备维修拆卸工序规划中的有效性。基于以上研究，定义基本拆卸结构应包括被拆卸的父节点、拆卸得到的子节点、拆卸关系3个要素，基本拆卸结构如图1a所示。

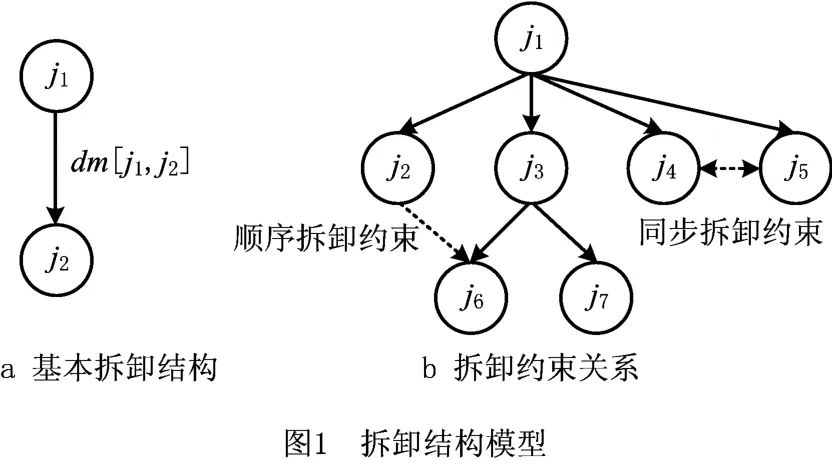
父节点表示该结构拆卸前的形态；子节点表示父节点经过拆卸后得到的部件，一个父节点被拆卸后可以得到一个或多个子节点。对于每个节点，可定义节点j的拆卸时间，以表达拆出该子节点付出的时间；定义拆卸成本率，通过拆卸成本率与拆卸时间的乘积来表达拆出该子节点付出的拆卸成本。

定义任意两节点j1和j2间的拆卸关系dm［j1，j2］，主要存在3类拆卸关系：①两节点间无直接拆卸关系。②若j1可被直接拆卸，则可以拆卸j1获得j2并付出相应的拆卸成本和拆卸时间，该拆卸关系称为父子拆卸关系，记为j1→j2，如图1b中j1和j2所示。③对于复杂的拆卸结构，由于存在各类空间、结构约束，非父子关系的节点间也可能存在两种特殊的拆卸约束关系，即同步拆卸约束和顺序拆卸约束。同步拆卸约束指当需要拆出某一节点时也必须同时拆出另一节点，如图1b中的j4和j5所示；顺序拆卸约束指当需要拆出某一节点时，必须优先拆卸得到另一非父节点，如图1b中的j2和j6所示。为记录拆卸树中任意节点对之间的拆卸关系，可建立拆卸关系矩阵dm［j1，j2］，

基于上述模型，可构建一棵N叉拆卸树，以表达多部件系统的拆卸结构，该树应具有以下特点：①是连通的有向图和无序树，拆卸过程由上至下，同父的兄弟节点间无顺序；②根节点唯一，代表拆卸前的完整系统，中间节点拥有至少2个子节点，叶节点不拥有子节点；③可假设故障原因能追究到最小拆卸单元，即叶节点；④维护对象是叶节点，不能是未完全拆卸的中间节点。

2.2 拆卸序列规划

由于结构复杂的多部件系统拆卸过程中包括多道拆卸作业，需引入拆卸序列规划。将从根节点出发、通往任意节点j的拆卸过程中涉及的所有节点组成的有序集合，称为节点j的拆卸路径path（j）。该路径可通过包含递归的树形结构遍历算法求得，算法流程如图2所示。对于有环的环状、网状拆卸结构，可采用Dijkstra算法求解最短路径。

图2中：j为目标节点；root为根节点；｛J｝为拆卸树中所有节点的全集；cur为当前遍历点；a，b和c分别表示与当前遍历点存在同步、顺序、父子拆卸约束关系的三类节点（因可能存在多个同步、顺序约束节点，故建立数组｛A｝，｛B｝保存a，b，假设｛A｝，｛B｝各有ka，kb个元素）。根据树形遍历算法，通往任意节点j的拆卸路径path（j）可表达为

式中∪表示数组的并集运算；式中包括对path（A［k］）和path（B［k］）的递归。

根据拆卸路径path（j）和每个节点的，可以计算沿该路径进行拆卸所需的拆卸总时间和总成本。定义从根节点出发、拆卸至某节点jx的拆卸总时间为DT（jx），相当于路径上所有涉及的节点拆卸时间的总和，可表达为

同样地，路径上的拆卸总成本相当于路径上所有节点的拆卸成本率与拆卸时间乘积的和，定义从根节点出发进行拆卸至某节点jx的拆卸总成本为DC（jx），

考虑到机会维护时多个部件一同维护的特点，也需要定义并计算从根节点出发、前往多个节点的总路径以及该路径下的拆卸时间和成本。假设当一个部件jx进行故障或预防维护时，其余进行机会维护的部件为jOM。因为可能存在多个jOM，所以将其置入机会维护节点的集合｛jOM｝，假设｛jOM｝共有K个元素。

因此可将从根节点出发、前往目标节点jx和机会维护节点组｛jOM｝的拆卸总路径称为合并路径path′（jx，｛jOM｝）。该路径path′（jx，｛jOM｝）通过jx的路径path（jx）与｛jOM｝中每个节点的路径path（jOM［k］）求并集得到，可表达为

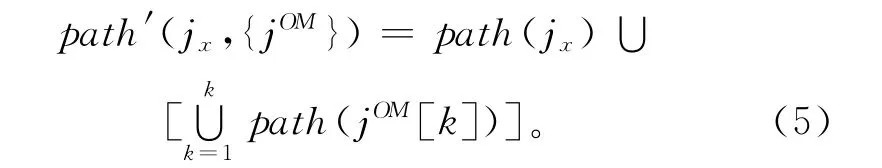
根据path′（jx，｛jOM｝）可进一步求得该路径下的拆卸总时间和拆卸成本。其中，前往jx和｛jOM｝的合并路径下的拆卸时间可定义为

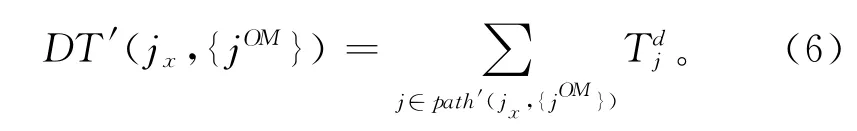
合并路径下的拆卸成本可定义为

3 考虑拆卸和随机故障的机会维护策略与建模

3.1 部件层的预防维护策略与建模

通常可以认为部件的可靠性服从威布尔分布，θj和βj为该分布的特征寿命和尺度参数，则定义部件j在t时刻的瞬时故障率λj（t）、在（t1，t2）时间段的累计故障次数Lj（t1，t2），分别表达如下：

对于单部件j，在一个预防维护周期内，若发生随机故障则进行故障维护，否则在其使用役龄达到设置的预防维护间隔Tj时进行预防维护。对于一个周期，周期长度由预防维护间隔和停机总时间组成，周期内的总成本由故障维护成本或预防维护成本、拆卸成本和停机成本三部分组成，因此单个周期内的维护成本率

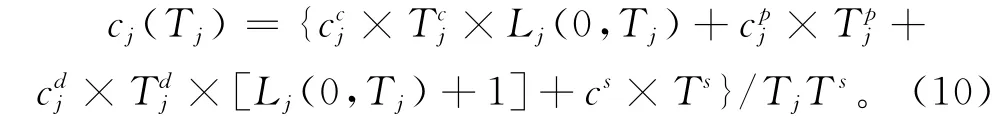
基于维护成本最小化的策略，对每个部件j均分别以Tj为决策变量、以最小化单周期内的维护成本率cj为目标进行优化。通过对维护成本率cj关于预防维护时间间隔Tj求导，由推得函数极值，可求解出各部件j的最优预防维护间隔数值解。

3.2 系统层的机会维护策略与建模

通常，任意部件发生随机故障或预防维护时都将使整个系统停机，此时其余部件都存在机会维护的可能，可以通过基于机会维护时间阈值Tw的机会维护策略来决策如何整合部件的维护活动。该机会维护策略如下：在第i次停机中，各部件按照单部件最优预防维护间隔算法的理论维护时间分别为timei（j）（j∈｛J｝），其中必然存在唯一的某部件ji相对于其他部件率先达到其下次预防维护的时刻点，该时刻点timei为

以该时刻点timei为系统第i次停机维护的时刻，部件ji即为必须维护的对象。

再定义机会维护时间阈值Tw，Tw以时间长度为单位，它决定了其他拥有维护机会的部件j（j≠ji）的下次预防维护时刻点timei（j）距离当前时刻timei有多近时才进行机会维护。具体地，如果满足timei（j）≤timei+Tw，则合并维护活动，将进行机会维护的部件j标记为（进行机会维护的部件可能存在多个，因此将其置入集合｝中），其下次预防维护提前到当前时刻与部件ji一同进行，而该部件未来的预防维护计划也将动态调整。相反地，如果满足timei（j）＞timei+Tw，则放弃合并j，仅对必须维护的部件ji及其他满足条件的部件分别进行故障或预防维护和机会维护。

在此策略下，定义第i次停机时间ti由三部分组成，分别为ji的故障维护或预防维护时间、机会维护部件组的维护时间及其拆卸时间：

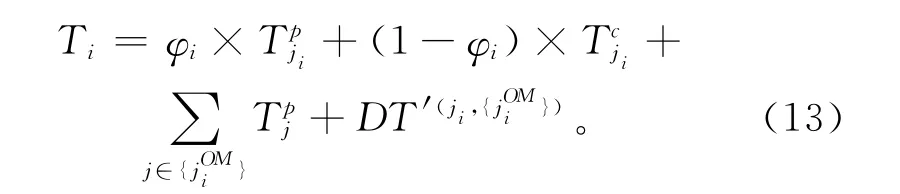
同样地，定义第i次停机维护成本Ci由故障维护或预防维护成本、机会维护成本、拆卸成本以及停机成本组成，即

式中：I为全规划工作时间内的总停机次数；φi为维护活动类型，表示第i次停机进行的是故障维护或预防维护，

当调整Tw的取值时，将改变每次停机时进行机会维护的部件组合｝，并动态改变之后的全部维护计划以影响整个维护过程。使用动态规划方程法求解Tw的最优值，建立一个以机会维护时间阈值Tw为决策变量、以最小化全规划工作时间内的系统维护总成本TC为决策目标的规划方程：

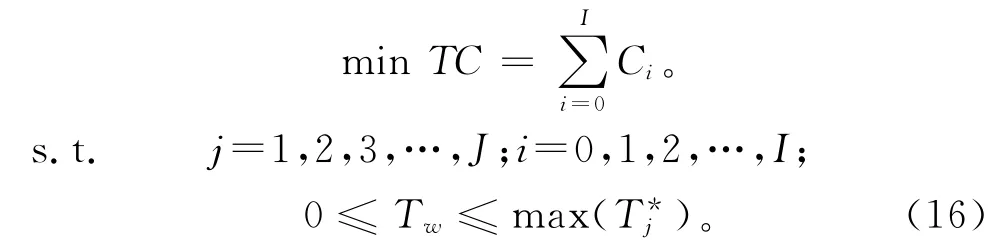
在Tw的有效值区间内，通过规划方程的枚举遍历来寻找一个Tw的取值，使得在该时间阈值下的系统维护总成本TC最小，该即为最优机会维护阈值。

4 算例分析

为验证所提模型和策略，设计一个规模合适的系统，以19个节点的N叉树模型表达的多部件系统为例。假设系统全规划工作时间Tdesign=3 000，单位时间停机成本Cs=10。

系统的拆卸结构以N叉树表达，该树包括1个根部件节点、6 个中间部件节点｛jⅡ，jⅢ，…，jⅦ｝和12个叶部件节点（j1，j2，…，j12），各节点间的拆卸约束关系如图3 所示，设置拆卸相关参数如表1所示。

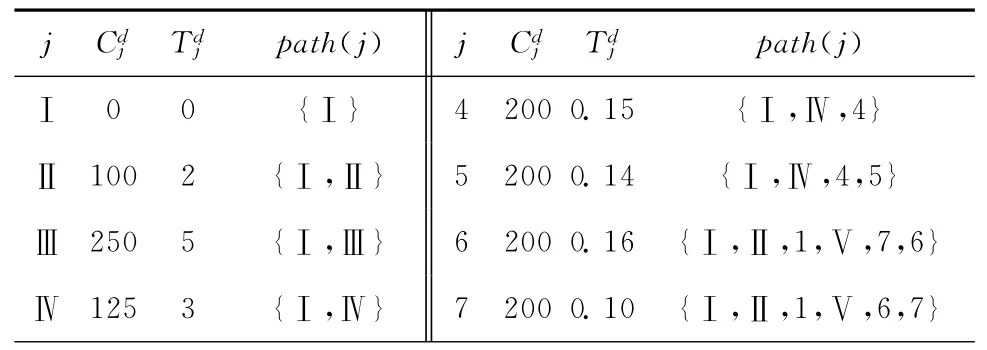
表1 节点的拆卸参数表

续表1

各叶部件节点｛j1，j2，…，j12｝由于也是维护对象，设置维护相关参数如表2所示，可计算出单部件最优预防维护间隔。

表2 叶部件节点的维护参数表

4.1 算例仿真

在Visual Studio 2008平台上，通过C++语言对算例编程并进行基于Monte Carlo仿真的数值分析。在仿真中将连续的时间离散化，将全规划工作时间Tdesign分割为若干个宽度为最小时间单元σ的微时间段dt。在算例中，考虑Tdesign=3 000的系统规模，取最小时间单元σ=1，则微时间段个数为3 000。对每个微时间段dt都单独进行仿真模拟，每个dt内的所有概率事件都以生成随机数的方式决定其是否发生。在出现随机故障或到达预防维护时刻点后，根据维护策略实施拆卸和维护活动，运行完整个Tdesign后将得到该维护策略下的总成本。通过不断调整维护策略中的决策量（即机会维护时间阈值Tw）进行更多仿真，找出所有维护方案总成本中的极小值TCmin，对应的机会维护阈值即为最优机会维护阈值。考虑到Tw的有效值范围较广，为控制仿真规模，以25为Tw的最小单位。

当仿真次数N足够多时，求取N次仿真的统计平均值，则概率事件不确定性的影响将被缩小，最终生成平滑的统计曲线。对算例进行仿真次数N=2 000的Monte Carlo仿真，结果如图4所示。

分析表明：经过2 000次Monte Carlo仿真后，统计曲线已趋于平滑，且存在唯一的极小值，极小值两侧的单调性较完好。目标函数极小值TCmin=315 43.6，即为最低的维护总成本，其对应的最优机会维护阈值，其他Tw方案下的总成本均高于此结果。

如果不进行任何机会维护，则可视Tw=0，由于Tw=0对应的目标函数值（TC=33 090）相当高，可以认为该策略优于不实施机会维护的一般预防维护策略。为验证考虑拆卸因素后的机会维护策略的有效性，再进行不考虑拆卸的一般机会维护策略下的仿真模拟，将其优化结果与原策略下的结果进行对比分析，如表3所示。

表3 考虑／不考虑拆卸的两种策略优化结果对比

对表3进行分析可知：在拆卸成本为0或不考虑拆卸成本时，一般机会维护策略得出的优化结果优于考虑拆卸的机会维护策略的结果；然而拆卸成本客观存在，当其不为0时，考虑拆卸的机会维护策略的优化结果优于一般机会维护策略。

4.2 拆卸成本影响分析

为检验拆卸对维护的影响程度，对拆卸成本进行影响分析，可从调整系统整体的拆卸成本及调整不同深度部件的拆卸成本两方面进行。

（1）调整系统整体的拆卸成本

以参数原值为对照组，对另外4组不同拆卸成本率（其他参数保持不变）的算例分别进行仿真分析。通过在对照组的拆卸成本率Cdj原值上乘以4个不同的调整倍率α（α=0.2，0.6，1.4，1.8）来调整系统整体的拆卸成本，分别进行N=2 000次规模的Monte Carlo仿真，结果如表4所示。

表4 各调整倍率下目标函数极值与最优机会维护阈值

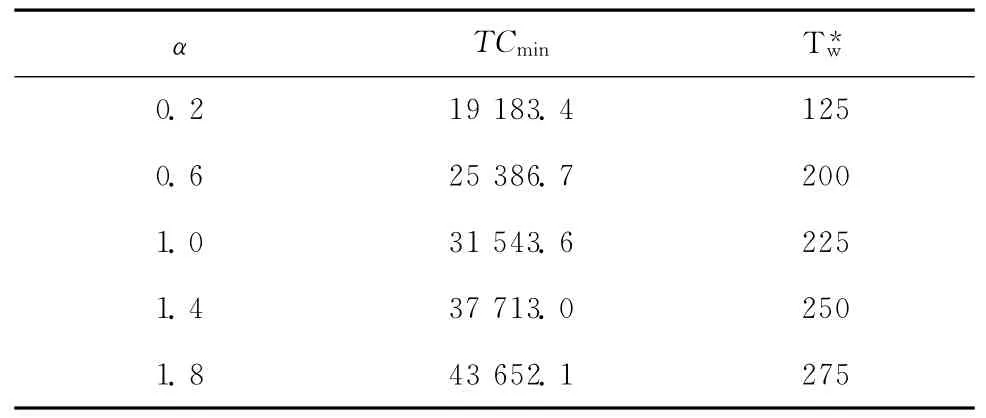
表4 各调整倍率下目标函数极值与最优机会维护阈值

考虑到调整倍率α对目标函数值的影响，为清晰地看出变化趋势，分别将另外四组函数曲线的数值缩放到与对照组一个数量级，保持极小值在同一水平线上，得到的结果如图5所示。

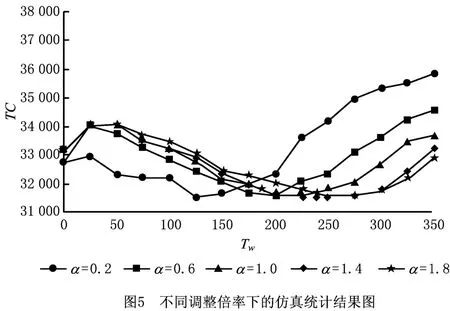
分析表4和图5可知：当保持其他成本参数不变时，随着拆卸成本率的递增，总成本递增，而成本函数曲线的极小点也在右移，表明对应的最优机会维护阈值递增。研究表明，当部件的拆卸成本较大时，将有更多部件加入机会维护中，支持在系统停机时实施更多的机会维护；而当拆卸成本较小时，研究结果更倾向于保守地实施机会维护。

（2）调整不同深度部件的拆卸成本

按节点深度depth［j］=2，3，4，5将所有非根的18个节点分为4层，每组仿真中分别对其中一层的所有节点的拆卸成本率乘以调整倍率α（α=0，2，5，10），其余层保持不变。进行N=2 000次规模的仿真，结果如表5所示。

表5 按节点深度调整成本对min TC 与的影响

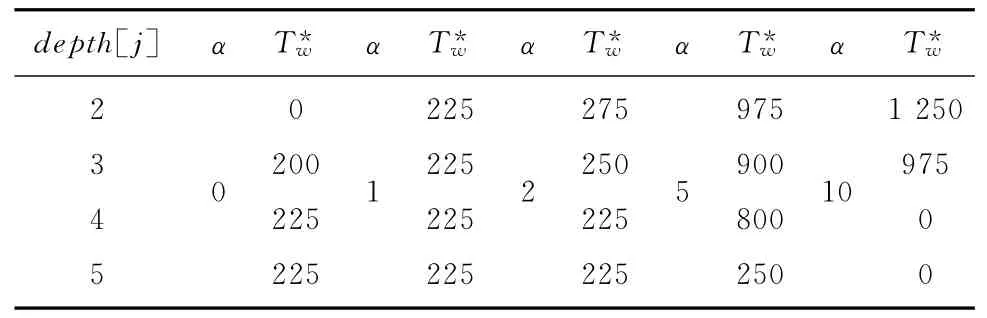
表5 按节点深度调整成本对min TC 与的影响

分析表明：浅层节点拆卸成本的变动将显著影响维护方案，说明维护总成本对浅层节点的改变具有更高的敏感性，而深层节点则相反。因此，当浅层的拆卸结构发生变化时，需要及时调整维护策略，企业也需要通过优化浅层的拆卸环节，以更高效地控制拆卸成本。

5 结束语

本文将拆卸理论引入设备维护，考虑随机故障发生时系统实施机会维护的可能性，在基于时间阈值的机会维护策略的基础上，建立了使用N叉树和拆卸序列规划表达拆卸结构的多部件系统机会维护模型。在算例研究中运用Monte Carlo仿真模拟了系统在全规划工作时间内的随机故障过程及动态维护决策过程，通过对机会维护时间阈值的优化有效降低了包含维护和拆卸在内的系统维护总成本，可促进设备维护决策和拆卸规划两个领域的交叉，为结构复杂且拆卸成本高的多部件系统提供更为经济的维护方案。

［1］ZHOU Xiaojun，LU Zhiqiang，XI Lifeng，et al.Opportunistic preventive maintenance optimization for multi-unit series systems with combing multi-preventive maintenance techniques［J］.Journal of Shanghai Jiaotong University（Science），2010，15（5）：513-518.

［2］DING Fangfang，TIAN Zhigang.Opportunistic maintenance for wind farms considering multi-level imperfect maintenance thresholds［J］.Renewable Energy，2012，45（1）：175-182.

［3］MA Ji，ZHAO Zhili，YAN Guangrong.Disassembly and assembly process planning for apparatus maintenance［J］.Journal of Engineering Graphics，2007，27（1）：42-47（in Chinese）.［马 骥，赵志力，闫光荣.维修拆装工艺规划系统的研究［J］.工程图学学报，2007，27（1）：42-47.］

［4］DU Jun，ZHU Xiaojun，PENG Fei.Research on maintenance and disassembly sequence optimization of ship equipment based on Petri net［J］.China Shiprepair，2008，21（4）：48-50（in Chinese）.［杜 君，朱晓军，彭 飞.基于赋时Petri网的舰船装备维修拆卸序列优化研究［J］.中国修船，2008，21（4）：48-50.］

［5］LIU Jia，LIU Yi.A disassembly CPN model for maintenance of airborne equipments with disassembly precedence constraints［J］.Journal of Computer-Aided Design &Computer Graphics，2011，23（2）：323-330（in Chinese）.［刘 佳，刘 毅.基于优先关系的飞机机载设备维修拆卸CPN 模型［J］.计算机辅助设计与图形学学报，2011，23（2）：323-330.］

［6］YANG Yuan，LI Fang，HOU Chongyuan，et al.Opportunistic group maintenance optimization of multi-unit system under dependence［J］.Computer Integrated Manufacturing Systems，2012，18（4）：827-832（in Chinese）.［杨 元，黎 放，侯重远，等.基于相关性的多部件系统机会成组维修优化［J］.计算机集成制造系统，2012，18（4）：827-832.］

［7］LIU Xinhua，PENG Gaoliang，LIU Xiumei，et al.Disassembly sequence planning approach for product virtual maintenance based on improved max-min ant system［J］.The International Journal of Advanced Manufacturing Technology，2012，59（5）：829-839.

［8］HOU Wenrui，JIANG Zuhua，JIN Yulan.Reliability-based opportunistic preventive maintenance model of multi-units serial-parallel system［J］.Journal of Shanghai Jiaotong University，2009，43（4）：658-662（in Chinese）.［侯文瑞，蒋祖华，金玉兰.基于可靠度的多设备混联系统机会维护模型［J］.上海交通大学学报，2009，43（4）：658-662.］

［9］DI Peng，LI Fang，YANG Yuan.Optimal preventive maintenance model based on opportunistic maintenance policy［J］.Chinese Journal of Engineering Design，2012，9（4）：263-267，273（in Chinese）.［狄 鹏，黎 放，杨 元.基于机会维修策略的预防维修优化模型研究［J］.工程设计学报，2012，9（4）：263-267，273.］

［10］KUO T C.Disassembly sequence and cost analysis for electromechanical products［J］.Robotics and Computer-Integrated Manufacturing，2000，16（1）：43-54.

［11］LAMBERT A J D.Exact methods in optimum disassembly sequence search for problems subject to sequence dependent cost［J］.Omega，2006，34（6）：538-549.

［12］GAO Diguang，PAN Quan，LIANG Yan，et al.Disassembly sequence planning based on information table and disassembly tree for maintenance［J］.Computer Applications，2006，26（3）：720-722（in Chinese）.［高地广，潘 泉，梁 彦，等.基于信息表和拆卸树的设备维修拆卸工序规划［J］.计算机应用，2006，26（3）：720-722.］