探析如何构建区域产业关联经济距离模型

周志英

（复旦大学 经济学院，上海 200433）

国民经济系统相对较为复杂，但在复杂的生产网络中，产业生产链的存在形式却总是有序的。产业之间关联的疏密程度对产业上下游联系具有重要反映作用，能够决定其紧密性。某种程度上还能决定某些重要的生产链，从而在产业结构的调整上为其提供决策依据。产业在国民经济系统中除了存在关联外，而且还存在经济距离。关联能够对产业之间联系程度的紧密性有所反映，经济距离则能够使产业之间中间生产环节的多少有所反映。通常来说，时间或空间尺度上的相隔长度即为距离所反映的，带有无向性，不管起始点选择哪里，客观实体之间的空间距离长度都是唯一确定的。当人的各种社会行为被引入后，距离除了可以用在对客体之间间隔长度的研究上外，还可以用在对相互之间联系的紧密程度加以反映方面。通过对区域产业关联经济距离模型的构建，我们可以更加直观的了解区域产业关联的紧密性。而在探讨如何对区域产业关联经济距离模型进行构建前，还应了解一下何为关联经济距离。

一、何为关联经济距离

某个产业（部门）与其他产业（部门）所反映在投入与产出中的关系，即属于关联。关联主要分为两种：其一为后向联系，即向该产业（部门）提供投入的上游产业与该部门两者之间的关联；其二为前向联系，顾名思义指该产业（部门）与它自身供给产出的下游产业（部门）之间所具有的联系。在研究关联的各种工具中，最为主要的是列昂惕夫逆系数。列昂惕夫在自己开创的投入产出宏观经济领域，对与产业关联有关的传统计算方法进行了大量研究，并被广泛应用在经济、环境和能源方面。感应度系数和影响力系数，是传统的产业关联当前所采用的对整个国民经济之间的前向及后向联系进行衡量的主要方式，不过这两种衡量方式对两个具体产业之间的联系却并没有涉及。

APL模型的提出者为荷兰投入产出学者Dietzenbacher等人，在这一研究过程中，他们将产业间经济距离概念引入其中。在该种模型之下，他们即可计算出平均层数，结果显示计算数值正相关于两个部门间的中间生产环节。即平均层次数越大，经济距离也会相应增大。他们不仅论证了列昂惕夫模型推导的后向APL，而且严格论证了Ghosh模型推导的前向APL，论证结果发现两者是相等的。层次数对生产链的影响是在APL模型中被首次考虑的，且两个部门之间的经济距离可以通过平均层次数来衡量，从而能够使两个部门之间生产环节的多少得到反映，所以在理论与实际方面具有一定意义。

影响力系数和感应度系数在参照的标准尺度上，选择的是整个国民经济所有部门的Leontief逆系数加和平均值，所以不管前向还是后向关联在每个部门中都可以进行比较，不过并没有涉及关联程度大小。在两个部门构成的某一条生产链上，虽然有可能具有很高的关联程度，但彼此之间在中间生产环节上也可能会相对较多，这就会导致它们之间具有较长的经济距离。或者虽然两个部门构成的某一条生产链上关联度并不算高，但彼此之间在中间生产环节相对较少，其在经济距离方面也就会比较短。虽然APL对两部门间经济距离的测算以生产链的平均层次数为依据，但对同一层次两部门间的关联大小却并不涉及。

以钢产品与其他产品在生产链构成中多层次关联示意图（见图1）为例可以看出，在1层的经济距离中主要为生铁、焦炭、电力等产品，而钢产品与这些产品的直接关联紧密程度从直接消耗系数可知一定存在相对差异。而在2层次、第3层次的经济距离上，钢产品与其他不同产品虽然是相等的，但差异同样存在于其关联紧密程度上。根据各个研究方法的优势，如何将其集结起来，不仅实现对任意两部门经济距离的测算而且将关联程度的大小反应出来，是当前仍然在探究的命题。因任意两部门最直接的关联程度可通过直接消耗系数来反映，所以需要对新的模型进行构建。

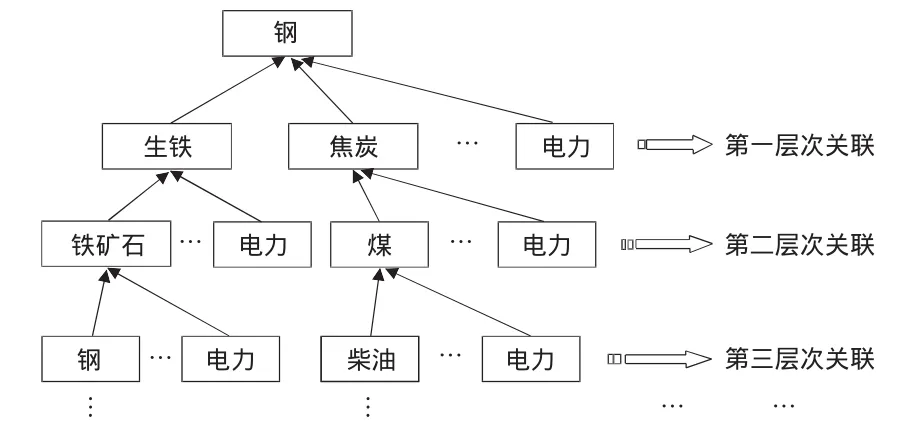
图1 钢产品与其他产品在生产链构成中多层次关联示意图

二、如何对区域产业关联经济距离模型进行构建

关联标准尺度比较，在APL模型中稍显欠缺，这种状况很难对部门关联程度进行准确反映。为了对任意两部门经济距离进行测算，并对其关联程度大小进行反映，我们必须构造标准生产链。在投入产出理论中，两个部门之间的直接关联可由每个直接消耗系数反映出来，与此同时两个部门构成的生产链是否完全关联，其构成部分中还包含直接消耗系数的乘积线性加和，在两部门间的关联程度上，两部门之间直接消耗系数的大小重要性主要体现在其决定作用上。j部门对i部门的直接消耗系数从公式上看，设投入产出表中的部门数量为n，那么两两部门之间在投入量上则可用n2来表示，两部门之间的平均投入量即，各部门的平均总投入，各部门直接消耗系数平均水平用公式来表示即为。

得出平均水平后，在此基础上则可构造标准尺度。进而推知，对标准生产链的构造上也可对直接分配系数加以采用。立足与标准生产链相比较的前提下，任意两部门构造的关联经济距离生产链都具有双重功能，其一可以反映部门之间的关联程度，其二则可以反映出经济距离信息。从这点来说，关联经济距离主要有两重属性，一种为关联程度，另一种为经济距离特征，且两种属性同时存在才可称关联经济距离。与空间距离的无向性相比，生产链是一种有序排列形式，处于产业之间上下游，方向性较强。所以，在对部门之间关联经济距离进行计算时，i，j部门构成的生产链形式是必须要考虑的，通常来说主要包括两种形式，一种表现在最终需求拉动上，还有一种表现在初始投入推动上。同样地，区域产业关联经济距离也有两种，一种为后向关联经济距离指数，另一种为前向关联经济距离指数。

（一）区域产业后向关联经济距离指数

当i，j部门构成的生产链形式为最终需求拉动时，其Leontief模型可见以下公式，即x=（I-A）-1f=Lf=（I+A+A2+…）f。f、x、A 在 Leontief模型中前者代表最终使用列向量，后者代表直接消耗系数矩阵，x 代表产出列向量，[A]ij为 xij/xj，xij为 j部门对i部门之间在直接消耗总量方面的表示。将标准尺度矩阵引入n个部门构成的国民经济系统中后，矩阵中所有元素都相等，即；矩阵元素：

对标准尺度进行引入后，矩阵系数形式则可用D来表示，用来代表任意i，j部门的标准生产链，即：

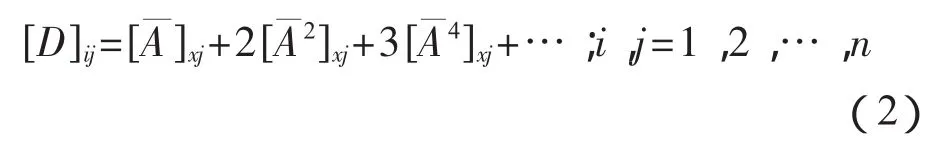
则对同一经济系统中任意i，j两部门后向关联经济距离指数Pij进行计算，可以得出：

其中

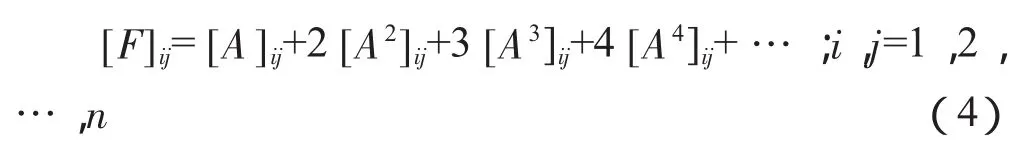
因为：

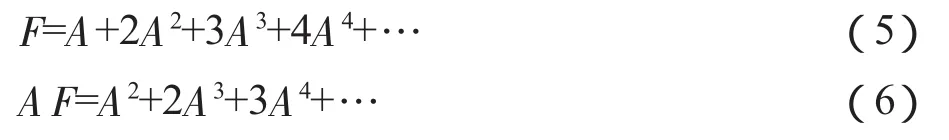
从 0≤[A]ij＜1，式（5）与式（6）相减及 Leontief模型式，易知 F=L（L-I）。同理可得。

作为常系数矩阵，A是该经济系统中所有部门资源配置为均等投入情况的代表，D列昂惕夫逆矩阵在均等投入情况下的代表。从式（1）和式（2）中可以明确，如果对标准尺度矩阵A采取引入行动，其所得到的结果将会是标准生产链中的每一层中任意两部门之间在关联标准方面都可以在其保证下实现统一性。所以关联经济距离式（4）可以用来比较标准生产链式（2）比较，最终得到式（3），从而可以在对任意两部门之间经济距离进行测算的过程中，使两部门关联程度的大小被反映出来。式（3）即为后向关联经济距离指数，站在最终需求拉动角度的视角来看，两部门构成生产链中关联程度随后向关联经济距离指数的增加而越加紧密，且中间生产环节越多，经济距离越大，反过来说同样可以成立。

（二）区域产业前向关联经济距离指数

初始投入推动的Ghosh模型为：

其中x'是对x的转置，w'是对w的转置。在这个公式中，w即为初始投入列向量，B即为直接分配系数矩阵，由此可以得出以下公式：[B]ij=xij/xi。在该公式中所代表的就是总产出对角阵，而G顾名思义代表正是Ghost逆矩阵。假设n个部门形成了国民经济系统，即可有；矩阵元素：

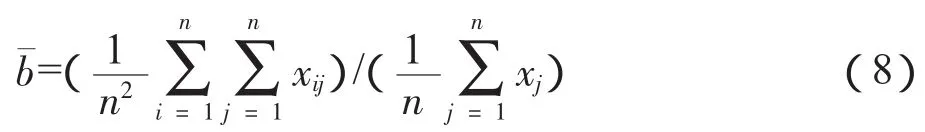
根据投入产出表中间流量及总产出加和可以得出：

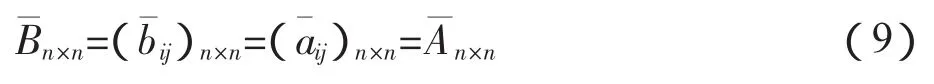
则对同一经济系统中任意i，j两部门前向关联经济距离指数Qij进行计算可以得出：

其中：

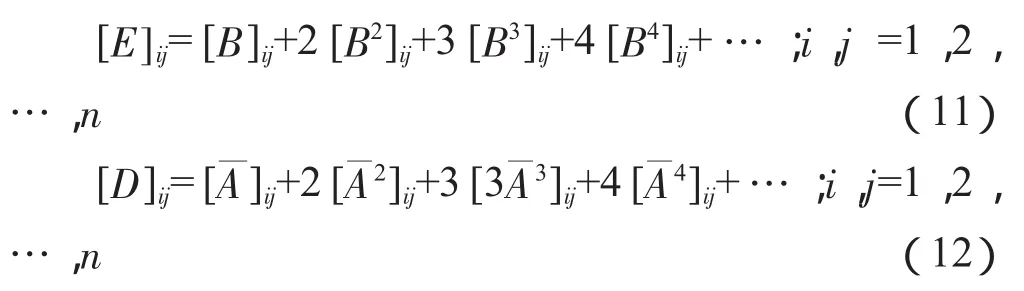
前向关联经济距离指数即为式（10），根据模型可以看出，站在初始投入推动视角来看，前向关联经济距离指数与两部门构成的生产链中关联程度呈正比，即前者越大后者紧密度越高，且中间生产环节越多经济距离越大，反过来也同样可以证明。对L模型和G模型在同一经济系统中分别进行采用时，如果后向关联经济距离指数用Pij来表示，前向关联经济距离指数用Qij来表示，计算它们之间的关系即可有E=G（G-I）。由于，所以当。所以：

即：

当X1=X2=X3=…=Xn时，可以得出：

从公式（14）可以看出，其实Q这一前向关联经济距离指数矩阵与P这一后向关联经济距离指数矩阵两者之间属于相似矩阵，相似变换矩阵则为其总产出的对角阵。如果各部门总产出处于相等的情况，向前与向后关联经济距离指数在同一经济系统中是相等的。

三、总结

对客体位置间长短进行反映，是空间距离这一概念存在的通常作用。人的社会行为与经济之间的关联与紧密程度并非一成不变的，当经济距离被引入后其彼此间的关联及紧密程度也成为这一概念需要反映的重要内容。本文在参照标准中引入标准生产链，并将投入产出关联度的优点与APL模型的优点结合起来，与标准生产链比较之后同一经济系统任意两部门构成的生产链都能够产生极大作用，这种作用除了表现在对两部门经济距离的反映上，还可以表现在对两部门之间关联程度的反映上。基于区域产业关联背景，本文对其关联经济距离模型的创建主要包含两部分，其一为前向关联经济距离指数，其二为后向关联经济距离指数。

因阈值在设定方面带有相对主观性，所以根据区域产业关联经济距离的构造模型，不仅可以引入标准尺度，而且可以对不同的主观标准实施引入。在这种模型范围中无论是对同一国民经济系统中部门之间经济距离的比较，还是对其关联度的比较都不会产生妨碍作用。在区域产业关联经济距离模型中，我们可以看见前向与后向关联经济距离指数都并非是具体值，而是均为相对值，在这种情况下部门之间在大小比较上并非是绝对大小的比较而是相对大小。根据构造的模型来说，前向与后向关联经济距离指数矩阵其实有些相似，不过这种相似在部门的总产出对角阵上的体现看起来并不那么相似，而是通过相似变换矩阵表现出来。根据各部门总产出的相对大小来进行计算可以发现，这种结果除了会在两部门间前向关联经济距离方面的相对大小有决定作用，同时对两部门间后向关联经济距离相对大小也有决定作用，此外直接消耗系数和直接分配系数直接关系着关联程度，即产业部门之间的联系紧密程度与国民经济系统生产技术架构也有相对关联，会受到其影响。

无论在什么时代，国民经济都会或多或少受到产业结构调整的影响。在当前国民经济可持续发展大环境和发展目标中，产业结构的调整无疑是一个重要的实现低碳经济的途径，通过上下游传递，任一产业规模与生产技术的变动都会对不同区域所有产业产生影响和波及。所以，面对当前对低碳经济不断推广的新经济背景，在制定相关决策前，区域产业结构必须认识到自身调整某一产业过程中可能带来的影响，并对其尽可能地进行充分估计。在需找一些关键生产链时，可依托区域产业关联经济距离模型进行计算。计算结果如果显示生产链在关联程度上缺乏紧密性，存在较多的中间环节，经济距离较大，相对其它产业调整带来的影响效果将较少，而反之则具有直接有效的影响，可以为相关部门对产业规划进行制定的过程中提供更多参考。

[1]殷广卫，李佶.空间经济学概念及其前沿——新经济地理学发展脉络综述[J].西南民族大学学报：人文社科版，2010（1）：33-34.

[2]曹博，马雯雯，郭亚楠.空间经济学——经济学新的探索领域[J].经营管理者，2009（18）：101-102.

[3]潘文卿，刘起运.区域经济的空间联系：方法与指标[J].统计研究，2004（10）：60-63.

[4]邓志国，陈锡康.中国部门生产链演化趋势及动态影响分析[J].运筹与管理，2009（5）：88-89.

[5]刘红光，刘卫东，唐志鹏，范晓梅.中国区域产业结构调整的CO2减排效果分析——基于区域间投入产出表的分析[J].地域研究与开发，2010（3）：25-27.

[6]韩嵩.区域产业关联与波及效应统计指标体系及测算[J].统计与决策，2012（7）：44-45.

[7]韩斌，刘朝明，李亮.MRIO模型在区域间产业关联强度研究中的应用[J].生产力研究，2007（16）：115-117.

[8]全诗凡.基于区域产业链视角的区域经济一体化——以京津冀地区为例[D].南开大学博士学位论文，2014：12-13.

[9]王德忠，庄仁兴.区域经济联系定量分析初探——以上海与苏锡常地区经济联系为例[J].地理科学，1996（1）：51-57.

[10]胡朝霞.两岸三地贸易关系的实证研究——基于变系数面板数据引力模型的分析[J].中国经济问题，2010（6）：64-71.

[11]唐志鹏，刘卫东，刘红光.投入产出分析框架下的产业结构协调发展测度[J].中国软科学，2010（3）：90-92.

[12]彭连清.我国区际经济联系与产品流动的实证分析[J].生产力研究，2008（5）：68-69.