基于高频数据的动力煤与焦煤价格联动效应研究

顾 鹏，张杰斌

（南京大学 工程管理学院，江苏 南京 210093）

一、研究目的

近年来，随着全球经济不断发展，各国在能源的生产、消费和贸易方面存在不同程度的增长。根据《BP世界能源统计年鉴》的报告，在 2012年全球能源消费结构中，石油占据最大的比例，为33%，其次是煤炭和天然气，分别占比 30%和24%，水电、核能和其他可再生能源占比 13%。由此可见，石油、煤炭和天然气是当今世界的主要能源，它们的稀缺性和不可再生性导致了世界各国对能源的竞争越来越激烈，由能源引发的冲突和战争与日俱增。

与世界上多数以石油为主导型能源的国家不同，我国的能源消费以煤炭为主，煤炭的生产量和消费量居于世界首位。我国煤炭消费量占世界煤炭消费量的50%左右。煤炭是我国最主要的基础能源，在我国的能源消费结构中，煤炭占比一直维持在 70%左右，2013年占比近 66%，煤炭对我国国民经济起着决定性作用。但是近几年来我国煤炭消耗比重呈下降趋势，主要是由于国家为治理雾霾调整能源结构减少了煤炭消费量，而煤炭的替代能源消费量却逐渐增多，但是我国“富煤、贫油、少气”的能源储备特点和煤炭相对低廉的成本决定了在未来较长的时期内，以煤炭为主的能源消费结构仍将继续维持，根据《煤炭产业经济政策研究报告》预测，到 2020年煤炭在中国一次能源消费结构中还将超过 50%，因此，煤炭问题可以说是我国能源的主要问题，而煤炭问题的最主要方面是实现煤炭价格相对稳定，确保国家经济安全。

煤炭是我国最主要的基础能源，在我国的能源消费结构中，煤炭占比一直维持在 70%左右，2013年占比近66%，煤炭对我国国民经济起着决定性作用。但是近几年来我国煤炭消耗比重呈下降趋势，主要是由于国家为治理雾霾调整能源结构减少了煤炭消费量，而煤炭的替代能源消费量却逐渐增多，但是我国“富煤、贫油、少气”的能源储备特点和煤炭相对低廉的成本决定了在未来较长的时期内，以煤炭为主的能源消费结构仍将继续维持，根据《煤炭产业经济政策研究报告》预测，到2020年煤炭在中国一次能源消费结构中还将超过 50%，因此，煤炭问题可以说是我国能源的主要问题，而煤炭问题的最主要方面是实现煤炭价格相对稳定，确保国家经济安全。

在期货交易中，跨品种之间的交易一直是投资者主要交易策略之一，其中的主要交易品种是玉米、小麦等农产品。2013年焦煤期货和动力煤期货的推出为跨品种交易提供了更好的交易产品。一方面两者都属于煤炭的同类品种，其下游行业之间相关性也较大，现货价格之间存在高度相关性；另一方面，我国煤炭的现货市场交易量巨大，动力煤期货与焦煤期货的交易量也必然可观。

从动力煤与焦煤价格的历史走势中可以发现，两者的走势惊人的相似，动力煤期货与焦煤期货之间是否也存在着一定的关联性，其联动效应究竟如何，目前学术界尚未对这一问题有所涉猎，为此，本文将对这一问题进行研究。

二、文献综述

（一）煤炭和其他能源市场的相关性研究

目前国内外学者对煤炭市场和其他能源市场之间的相关性进行了一些实证研究，这些研究主要利用均值 Granger因果检验、协整分析、VAR模型以及方差间的 Granger因果检验。一部分学者对煤炭市场与其他能源市场之间的长期均衡关系和均值溢出效应进行了探讨。

Bachmeier和 Griffin（2006）[1]研究了原油、煤炭和天然气三个能源市场自身内部的整合程度以及三者之间的一体化程度，他们发现世界石油市场是一个单一的高度整合的经济市场，煤炭价格在美国五个交易地区虽然也是协整的，但是整合程度要低很多，而原油、煤炭和天然气三个市场之间的一体化程度非常弱。

Manzoor等人（2011）[3]采用自回归分布滞后模型（ARDL）研究了原油、天然气和煤炭价格之间的关系，结果表明三者之间存在长期均衡关系。Mohammadi（2011）[4]用协整检验和 VAR 模型对美国石油、煤炭和天然气价格之间的关系进行了研究，发现三种能源价格之间存在一个协整关系，但是煤炭的价格不会受到石油和天然气价格的影响。

国内学者近年来也开始关注煤炭价格与其他能源价格之间的关系，既有定性分析又有定量分析。张同功（2005）[5]、袁桂秋（2009）[6]、蔡鑫磊（2008）[7]、战彦领（2008）[8]等学者对我国煤炭价格影响因素进行了分析，指出了石油价格对煤炭价格有正向影响。焦建玲（2007）[9]利用时间序列对煤炭需求与收入、煤炭价格和石油价格进行了建模，结果发现三者之间存在长期协整关系。

张志杰等人（2013）[10]通过协整分析、Granger因果检验、脉冲响应等方法对 2002年 1月至2012年 12月之间 Brent原油、大庆原油、澳大利亚BJ动力煤现货价以及秦皇岛大同优混平仓价的月度数据进行了分析，结果显示国内外石油与煤炭价格存在长期协整关系，国际油价是国内能源价格的格兰杰原因，国内油价、国际煤价是国内煤价的格兰杰原因，国内油价是国际煤价的格兰杰原因。

张坤等人（2013）[11]通过建立 VAR和 VECM模型研究了煤、石油、天然气和铀的价格之间的关系，研究表明这四种能源价格之间具有长期均衡关系，且铀价对煤价有反向作用。近年来，除了考察不同能源市场之间的价格溢出效应，许多学者开始研究煤炭市场与其他能源市场之间的波动溢出效应。

何琬（2011）[12]利用 BEKK-MGARCH 模型对石油与煤炭价格之间的波动溢出效应进行了实证分析，她选取了 1998年 1月到 2010年 6月之间秦皇岛港大同优混平仓煤价和大庆原油价格，发现两者之间既有正相关关系，又有显著的双向非对称波动溢出效应。

（二）不同地区煤炭市场的相关性研究

除了研究煤炭市场与其他能源市场之间的相关性之外，少数文献也对不同地区煤炭市场之间的相关性进行了研究。Monika等人（2013）[13]探讨了不同地区动力煤市场之间的相关性，他们采用了2002年4月1日到2011年12月30日期间太平洋和大西洋市场中最大的进出口商的动力煤市场价格周数据，并运用ARMA-EGARCH模型对均值溢出效应和波动溢出效应进行了分析。分析指出不同市场之间的相关性程度是不同的，来自同一市场的参与者之间的相关性最强（无论是大西洋市场还是太平洋市场），澳大利亚煤炭价格是形成太平洋市场价格最重要的因素，阿姆斯特丹-鹿特丹-安特卫普港口和理查兹湾港口的煤炭价格对大西洋市场煤炭价格的影响最大，并且是太平洋地区煤炭价格的Granger原因。

徐进亮等人（2013）[14]计算得到 2003—2013年我国秦皇岛大同优混煤月平均价格与澳大利亚BJ动力煤现货月平均价格的相关系数高达0.907，因此认为我国大同优混煤价格与澳大利亚BJ动力煤现货价格的波动趋势基本一致。

雷强（2013）[15]通过协整分析、误差修正模型、脉冲响应和方差分解等方法研究了国际动力煤价格和我国动力煤进出口之间的相互关系。通过研究发现，我国动力煤进出口和国际动力煤价格之间存在长期协整关系。此外，我国动力煤出口和国际动力煤价格短期内存在双向因果关系，但是两者不存在持续影响。

综上所述，我们可以发现国内外学者对煤炭市场与其他能源市场之间的相关性做了较多的研究，国外学者虽然对不同煤炭市场之间的相关性也进行了一些研究，但是多数局限于研究不同煤炭市场之间的长期均衡关系以及均值溢出效应，对不同煤炭市场之间的波动溢出效应研究非常少，而且这些研究中基本不涉及中国市场，国内学者极少有针对不同煤炭市场之间相关性的研究。目前的研究空白为本文的研究提供了空间。

关于不同金融市场之间联动性的研究，目前学术界的研究主要从两个维度来开展，分别为均值溢出效应以及波动溢出效应。

关于联动效应的研究主要分为三方面。第一类是跨市场研究，主要考察同类型金融市场在不同地区之间的溢出效应，比如不同国家股票市场之间的联动性研究（Caporale，2002[16]；Zhong、Darrat和 Otero，2004[17]）、不同国家之间期货市场之间的联动性研究（杨婷、刘金山，2013）[18]。

第二类主要针对的是同一国家内金融产品与其衍生品之间的联动性研究，比如股票市场与股指期货市场之间的联动性研究（Brooks、Rew、Ritson，2001[19]；严敏、巴曙松、吴博，2009[20]；封思贤、张兵和李心丹等，2010[21]）。

第三类是跨品种研究，即对同一国家内同类别但不同品种之间进行定性分析，随后通过计量模型来对这种联动效应进行回归检验。比如说股票市场与外汇市场（Bahmani-Oskooee、Sohrabian，1992[22]；周杰琦和何中正，2009[23]）、大豆期货与豆粕期货（Simon，1999[24]；李新建、吴春梅和黄敏学，2011[25]）。

在均值溢出效应研究方面，Larson（1960）[26]以及 Stevenson和 Bear（1970）[27]分别对不同时间段美国的玉米期货价格相关性进行研究。Simon（1999）发现CME上市的大豆、豆油及豆粕期货存在协整关系。关于均值一处效应的研究方法，Bahmani-Oskooee 和 Sohrabian（1992）[28]采 用 协 整关系检验和 Granger因果关系检验，Brooks、Rew、Ritson（2001）使用了向量自回归模型（VAR）和误差修正模型（VECM）。近些年，Hengyun Ma，Lex Oxley（2010）[29]采用面板协整检验的方法对中国主要的能源之间价格相关性进行了分析。庄新田（2006）[30]，张兵、刘丹（2012）[31]和张志杰、罗世兴（2013）均运用VAR模型分别对国债、期货市场和原油进行了研究。李新建、吴春梅和黄敏学（2011）等运用相关性检验、协整关系检验、VECM模型等方法，对我国棕榈油、豆油和菜籽油期货之间的联动性进行了分析，研究表明三个品种之间存在着稳定的均衡关系。

对于不同市场之间波动溢出效应的研究中，目前学术界主要采用的方法是基于GARCH族模型。Chan（1991）[32]和 Koutmos and Tucker（1996）[33]分别采用GARCH-M和二元GARCH模型对标普500及其股指期货的波动溢出效应进行研究。Caporale（2002）采 用 BEKK 模 型 ，Tse（1999）[34]、Zhong、Darrat and Otero（2004）和 Monika Papiez、Sławomirmiech（2013）均采用了 E-GARCH 模型研究波动溢出效应。国内研究方面，严敏、巴曙松和吴博（2009）发现沪深300指数及其期货之间不存在显著的波动溢出效应。封思贤、张兵、李心丹和汪慧建（2010）利用BEKK-GARCH模型则发现我国的上证指数和及其股指期货之间存在显著的波动溢出效应。此外，还有周杰琦、何中正（2009）运用二元E-GARCH模型，邢精平、周伍阳和季峰（2011）[35]运用了多元的T-GARCH模型以及李晓明、万昆和柳瑞禹（2012）[36]采用 GARCH模型和EGARCH模型。

对于小波分析的应用也有很多，如Ramsey、Usikov 和 Zaslavsk（1994）[37]，Rua、Nunes（2009）[38]，宿成建、刘星和刘礼培（2004）[39]，侯守国、张世英（2006）[40]，金秀、王佳星和刘烨（2010）[41]以及杨婷、刘金山（2013）。

对于联动性的一般研究思路可以概括为：通过对样本序列的平稳性检验、协整关系检验、Granger因果关系检验，构造向量自回归模型或是误差修正模型，通过对相应参数的显著性检验来判断均值溢出效应，并在此基础上进行脉冲效应分析及方差分解，进一步阐述均值溢出效应的表现形式。随后通过ARCH效应检验，构建多元GARCH族模型，通过对相应参数项的显著性检验来判断波动溢出效应。本文也将采用这一成熟的研究框架，随后运用小波分析的方法，对波动溢出效应的表现形式进行进一步的阐述。

三、数据与研究方法

（一）数据

由于动力煤与焦煤期货是2013年才上市的品种，本文选取郑商所和大商所两种期货从2013年10月8日到2014年3月7日每天8∶59-10∶14、10∶30-11∶30、13∶30-15∶00 交易价格；交易数据频率选取为1分钟的高频数据，每个价格序列的数据样本为23 083个，数据来源为wind数据库。

在本文研究中RDM代表动力煤期货的收益率，RJM代表焦煤期货的收益率，收益率具体的计算公式为：

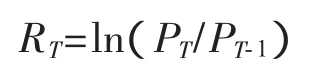
其中PT代表T时刻期货的收盘价格，PT-1代表T-1时刻期货的收盘价格。表1为动力煤与焦煤期货收益率序列的描述性特征分析。

表1 动力煤与焦煤期货收益率的描述性分析

（二）均值溢出效应研究方法

1.单位根检验。在进行协整关系检验之前，首先要对所要研究的时间序列进行平稳性分析，金融序列的平稳性检验又称为单位根检验。研究中经常采用的的方法有两种：DF检验（或ADF检验）和Phillips-Perron检验。

ADF检验的一般形式为：

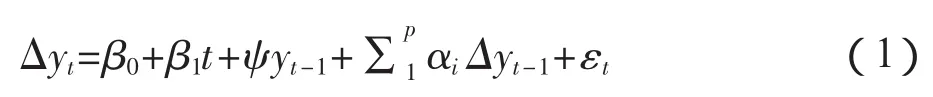
其中β0代表常数项，β1t代表随时间变动而变动的趋势项，在实际检验中需要确认是否要包括这两项，至于滞后阶数p的确定，一般采用AIC法则或是SC法则。

如果计量模型中所用到的扰动项存在ARCH效应时就会用到PP检验，PP检验的检验方程为：

2.协整关系检验。本文采用Johansen检验来验证动力煤期货与焦煤期货之间是否存在协整关系。使用Johansen检验，如果待检验的时间序列只有一个单位根，那么所需的检验方程就是：

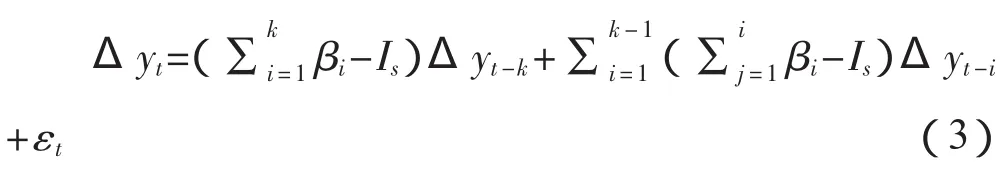
其中Is是一个单位矩阵，其具体的阶数为s，k为滞后阶数。迹检验统计量λtrace（r）和最大特征值统计量λmax（r，r+1）的计算公式为：

3.VAR模型。VAR模型是将滞后项加入回归方程的一种模型，常用于对存在一定均衡关系的时间序列进行预测以及研究衡量某稳定系统当受到外界冲击时系统内部各变量的表现。根据向量自回归模型的定义，一个滞后p阶、含有两个变量的VAR模型的基本形式如下：

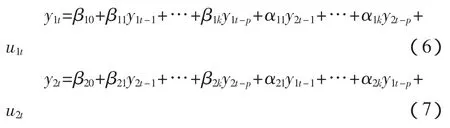
其中，uit是白噪声扰动项，并且满足条件：

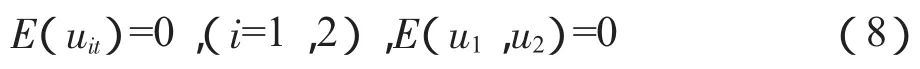
4.Granger因果关系检验。为确定变量之间影响方向，本文选取经典的Granger因果关系检验方法，其基本思想为：对于时间序列y1和y2，如果y1的变化会引起y2的变化，那么变量y1的滞后变量就会出现y2的回归方程中，并且对应的回归系数显著不等于0，此时可以说y1是y2的Granger原因。若同时y2也是y1的Granger原因，此时就可以说y1与y2存在双向的Granger因果关系。如式（6）和式（7）所建立的VAR模型，要想验证y1和y2之间是否存在Granger因果关系，只需检验假设α1i和 α2i是否等于 0（i=1，2，…，k）。

5.脉冲响应函数。VAR模型可以进一步考察某个给定变量的变化对系统内其他变量产生的影响是正向还是负向的，这个变量的变化对其他变量的影响将会在系统内持续多长时间，主要的方法就是脉冲响应（Impulse responses）。

用来描述变量之间影响机制的方法,我们称之为脉冲响应函数法。脉冲响应函数的基本思想是假设存在一个二元稳定的VAR系统模型如下：

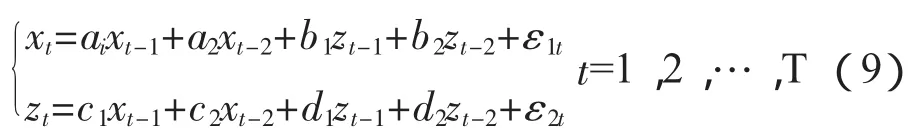
式中，ai，bi，ci，di是参数，扰动项 εt=（ε1t，ε2t）'是白噪声向量。

假定上述系统从0期开始活动，给定扰动项ε10=1，ε20=0，且其后均为 0，即 ε1t=ε2t=0（t=1，2，…）。并假设x-1=x-2=z-1=z-2=0。这就是在第0期给予脉冲，t=0时：

将其结果代入公式（9），当t=1时：

再把结果带入公式（9），当t=2时：

继续迭代下去，得到的{xi}序列称为来自变量x的脉冲导致的变量x的响应函数，{zi}的序列称为来自变量x的脉冲导致的变量z的响应函数，其中 i=0，1，2，…。

（三）波动溢出效应研究方法

1.ARCH模型及ARCHLM检验。ARCH（Autoregressive Conditional Heteroscedasticity）即自回归条件异方差模型，可以刻画金融数据所特有的“波动的集聚性”，其模型定义如下：

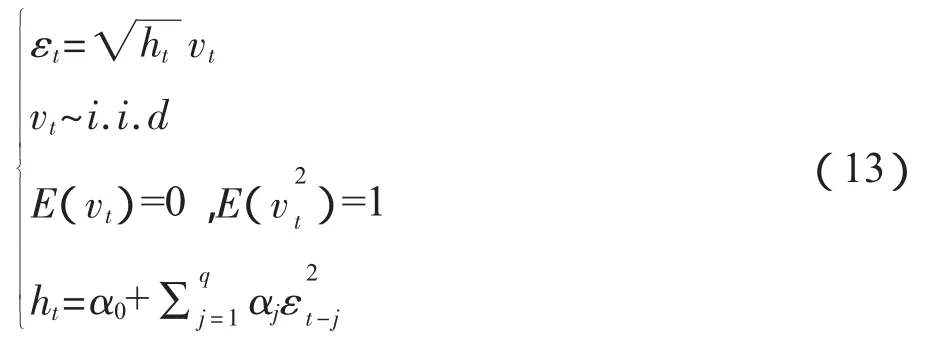
如果某一随机过程满足上述联立方程的要求，我们称这样的过程为滞后p阶的自回归条件异方差过程，一般记作ARCH（p）。

ARCHLM检验用来检验是否存在ARCH效应，其辅助的计量模型如下：

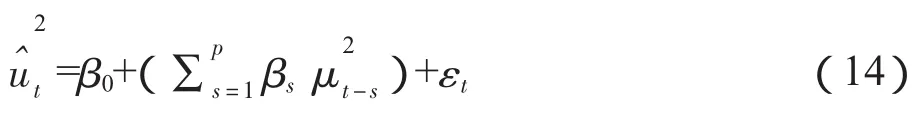
2.BEKK-GARCH模型。一般认为两个有关联的市场之间波动的影响与相互之间的风险传导机制、信息传递机制有关，而用于检验这种相互之间波动的影响常用的方法就是多元GARCH模型，本文研究中选择采用BEKK-GARCH模型。BEKK-GARCH模型的方差协方差矩阵形式为：

其中，εt为残差，Ω、B、A为待估参数矩阵。

结合本文研究所需，研究样本中的时间序列有两个，此时的BEKK模型展开的形式如下：

其中，ωij、αij、βij分别对应于矩阵 Ω、A、B 中的第（i，j）个元素。此时，h12代表市场一的条件方差，h22代表市场二的条件方差，h12代表市场一和市场二的条件协方差。

3.小波分析理论。假设函数ψ（t）满足平方可积条件，即 ψ（t）∈L2（R），如果通过傅里叶变换ψ（ω）可以继续满足下列可容许条件：

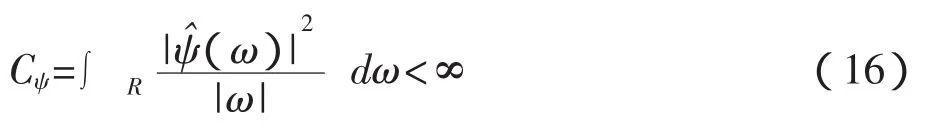
我们就称ψ（t）为一个基本的小波，也将该函数称为一个小波母函数。

在离散的情况下，小波基函数 ψa，（bt）为：

小波变换的函数形式定义为：

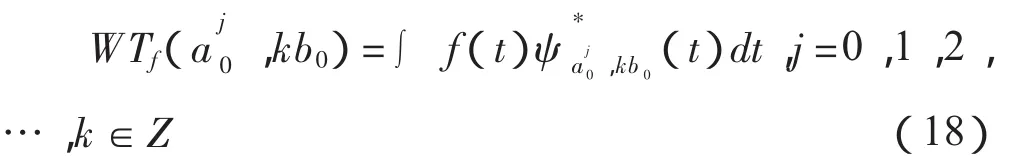
假设{Vj}j∈Z是空间L（2R）中的一个空间序列，那么小波多分辨分析指的就是{Vj}j∈Z要符合这几方面的条件：

（1）单调性，具体的函数形式为：Vj⊂Vj-1，j∈Z

（2）逼近性，具体的函数形式为：∩j∈ZVj={0}，

（3）伸缩性，具体的函数形式为：f（t）∈Vj⇔f（2t）∈ Vj-1

（4）平移不变性，具体的函数形式为：

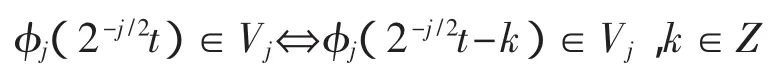
（5）Riesz基存在性，即：

存在一个小波基函数 φ（t）∈V0，令{φ（2-j/2tk）}k∈Z构成 Vj的 Riesz 基。

假定Vj代表通过小波多分辨分析得到结果中的低频部分而Wj代表其中的高频部分，那么我们就能得到这样的结论，即：

以（19）式为基准，我们就可以从分解的结果反响逼近到最初的待分解结果，用数学表达式可以得到：

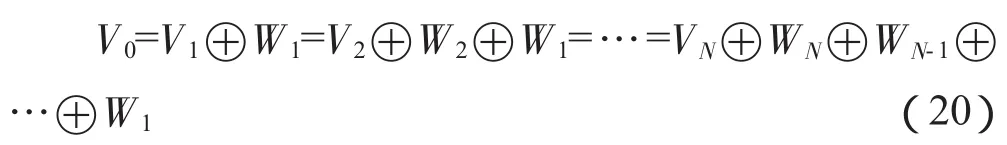
假定fj∈Vj表示小波分辨率为 2-j的低频部分的逼近，dj∈Wj代表高频部分的逼近，那么式（20）就转化为这样的形式：

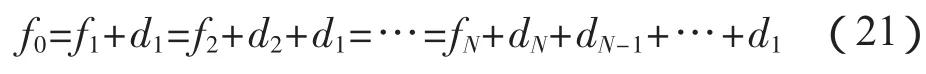
四、实证分析

本文采用的计量软件主要为Eviews 5.0，对小波分析使用的软件是Matlab 2014a。

（一）动力煤与焦煤期货均值溢出效应实证分析

1.平稳性检验。如表2所示，通过ADF检验和P-P检验结果表明，动力煤与焦煤的价格序列是非平稳的，而一阶差分序列则是平稳的，这表明二者均是一阶单整序列，即I（1）序列。对动力煤与焦煤期货的收益率序列的平稳性检验结果表明，收益率序列的平稳的。

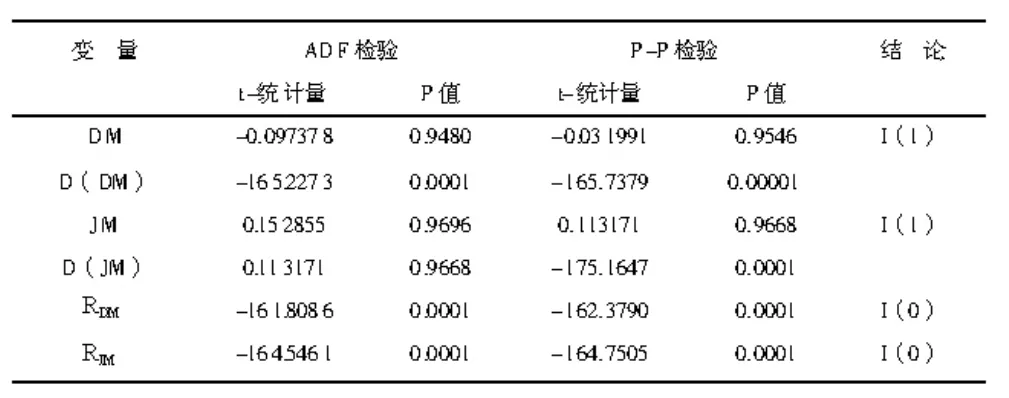
表2 动力煤与焦煤期货价格及收益率序列平稳性检验结果

2.协整关系检验。通过上述的时间序列平稳性检验，可以发现动力煤与焦煤的价格序列都是一阶单整的时间序列，这样就满足进行协整关系检验的条件。本文研究协整关系采用的方法是Johansen协整检验方法，表3为对动力煤与焦煤价格序列的协整关系检验的结果。

表3 动力煤与焦煤期货价格序列协整关系检验结果

回归结果表明，动力煤与焦煤价格序列之间存在着长期稳定的均衡关系，但并不是每一个模型都会体现这样的结果。这主要是因为动力煤与焦煤市场都是一个周期性的行业，这不仅表现在大的经济环境周期中动力煤与焦煤价格会随着经济的繁荣情况波动，而且表现在对于每一年的经济运行中。总之，我们得出这样的结论：动力煤期货与焦煤期货价格序列之间存在长期稳定的均衡关系。

3.VAR模型。结合前面对于VAR模型的描述以及上述平稳性检验的结果，本文研究中选取动力煤与焦煤期货的收益率序列作为回归的样本数据。在Eviews软件共有5种确定滞后期数，分别为 LR、FPE、AIC、SC、HQ法则，表 4中分别给出了五种法则确定的最优滞后期，其中SC法则和HQ法则最优滞后期为1阶滞后期，FPE法则和AIC法则的最优滞后期为4阶滞后期，而LR法则的最优滞后期为8阶滞后期，考虑到实际的滞后期不会太长，同时较长的滞后期会影响实际的回归影响效果，故在建立VAR模型选取法则和HQ法则确定的1阶滞后期。

根据上述最优滞后期选择结果，本文将构建动力煤与焦煤期货的VAR（1）模型，具体的模型回归结果如表5所示。

表4 动力煤与焦煤期货收益率序列V A R模型最优滞后期选择结果

表5 VAR（1）模型回归结果

从回归结果中可以发现，当为因变量时，存在第1期的自相关，且参数为负的，而作为自变量也是显著的，并且参数为正值，说明对存在正的均值溢出效应。同时当作为因变量时，作为自变量也是显著的，且参数符号为正，这说明对也存在正的均值溢出效应。这表明动力煤与焦煤期货之间是存在一定的价格联动效应。

图1的AR根图也表明，所有AR根的模的导数都处于单位圆内，表明之前设定的VAR（1）模型是稳定的，也说明之前验证的均值溢出效应是可行的。

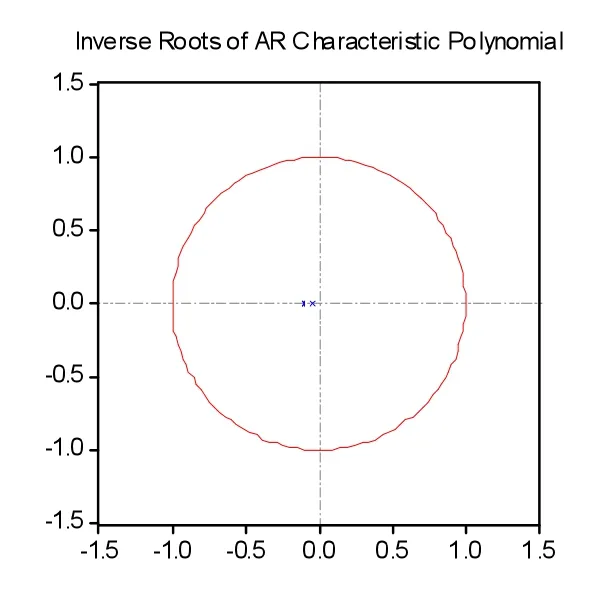
图1 VAR（1）模型的 AR根图

4.Granger因果关系检验。在建立完成VAR模型的基础上，接下来将进一步分析动力煤期货与焦煤期货相互之间是否领先滞后关系，Granger因果关系检验结果见表6。

表6 Granger因果关系检验的结果

结果表明，在5%的置信水平下，动力煤与焦煤期货互为Granger因果关系。这与当前我国经济形势有关，近些年来我国煤炭行业整体不景气，不论是动力煤还是焦煤，都经历着行业整体的严冬。Granger因果关系检验结果也表明，虽然动力煤与焦煤各自的工业用途不同，但二者同为国民经济基础行业的基础原材料，其价格之间必然存在一定的相互关系，这也与实际经验相符。

5.脉冲响应分析。前面已得出VAR模型是平稳的，因而下面进行脉冲响应分析也是稳定的。图2分别描述一个内生变量对来自于另外一个内生变量一个标准差的冲击的响应情况。

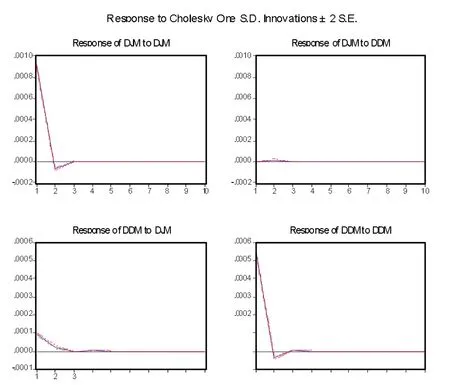
图2 脉冲响应分析图

左上角为焦煤价格收益率对来自自身一个标准差的脉冲冲击响应图。此情况下，从第一期开始焦煤价格的收益率会迅速降低，并且出现负值，直到在第2期达到最低值，随后收益率逐步反弹并且在第3期期初回复到正常情况，之前冲击所带来的影响也完全被吸收。

右上角为焦煤价格收益率对动力煤价格收益率的一个标准差的冲击响应图。在此冲击下，焦煤价格收益率从第1期开始会有很小幅上扬，随后从第2期开始逐步回落，在第3期冲击完全被吸收。

右下角为动力煤价格收益率对来自于自身一个标准差的脉冲冲击响应图。在此冲击下，动力煤的响应与焦煤的响应相似。

左下角为动力煤价格收益率对来自于焦煤价格收益率的一个标准差的冲击的脉冲响应图。此时，与焦煤的反应不同，动力煤价格收益率从第1期开始逐步回落，在第2期出现拐点，回落速度减缓，但仍继续下跌，直到第3期此冲击所带来的影响完全被吸收。

（二）动力煤期货与焦煤期货波动溢出效应实证分析

1.ARCH效应检验。根据之前提到的ACRH效应的模型，首先需要确定构建自回归模型的滞后阶数。通过分析可以得知，两个收益率序列的自相关函数和偏自相关函数都是在滞后一阶的情况下是显著后，这样我们构建了如下的检验模型：

其中c代表常数项，εt代表随随机扰动项。

随后我们在上述两个方程的基础上进行两个收益率序列的ARCHLM检验，具体的实证检验结果如表7所示。

表7 动力煤、焦煤期货收益率序列ARCHLM检验结果

通过实证结果可以发现，动力煤收益率序列的ARCH效应检验的F统计量和LM统计量从滞后1阶到滞后10阶的P值都基本等0.000，说明动力煤收益率序列存在显著的高阶ARCH效应，同样焦煤期货的收益率序列也存在显著的高阶ARCH效应。

2.BEKK-GARCH模型的构建。动力煤期货与焦煤期货原始收益率序列的BEKK-GARCH模型中相应的参数估计结果如表8所示。

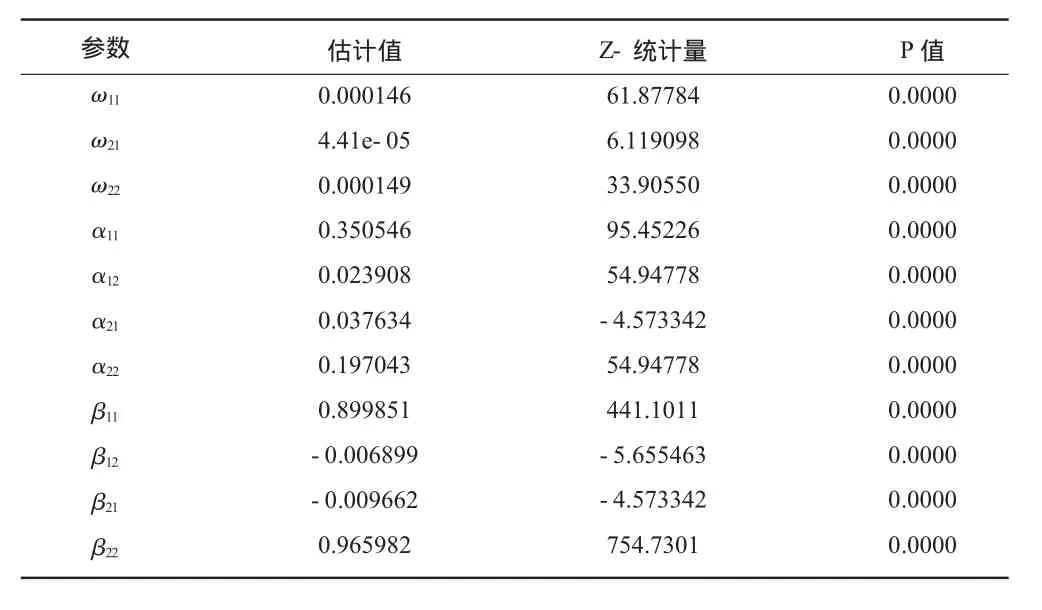
表8 BEKK-GARCHA模型回归结果

从回归结果可以看到，表示动力煤市场对焦煤市场波动溢出的参数α12、β12估计值在1%的置信度水平下都是显著的，即动力煤期货对焦煤期货存在显著的波动溢出效应。同样可以发现焦煤期货对动力煤期货也存在显著的波动溢出效应。因此我们得出结论：动力煤期货与焦煤期货市场存在双向的波动溢出效应。这表明在动力煤与焦煤期货市场之间存在一定的波动传导机制，这与二者共属于煤炭这一行业领域有关，同时二者所支持的下游行业都是关联性较为紧密的国家基础性行业有关。

3.小波分析。为分析在不同周期动力煤期货与焦煤期货之间的波动溢出效应，我们需要用到小波分析的方法来对原始的收益率序列进行频域上的分解，随后继续采用BEKK-GARCH模型进行分析。

因为 Daubechies（dbN）小波具有良好的正交性且降噪性能很好，可以使有限长度的时间序列进行正交小波分解和重构[42]，本文研究中将采用dbN小波来对两种期货收益率序列进行多分辨分析。一般N的选取范围是4～8。结合动力煤与焦煤期货序列的特性以及所选小波母函数的特点，本文最终决定选择db6小波。

在采用小波分析的方法对动力煤期货与焦煤期货的收益率序列进行多尺度分解时，需要对分解尺度进行准确的确定，而尺度的大小是由原始信号的情况以及具体分解时原始数据的采样率所决定的。[43]根据本文研究样本中动力煤期货与焦煤期货收益率序列的特征，结合以往的学术研究成果，决定进行小波多分辨分析的分解层数为5层。

根据以上参数的选择，分析结果如图3和图4，其中 s代表原有的收益率序列，di（i=1，2，3，4，5）表示的是各高频部分分解尺度所代表的收益率序列，a5表示的是低频部分反映的收益率序列。

从分解图中可以看到，各层分解结果都是平稳时间序列，同时都具有显著的自相关性以及波动集聚性，表明各个细分频域的时间序列均具有明显ARCH效应。接下来我们将对通过小波多分辨分解得出的各频域对应的动力煤期货与焦煤期货的收益率序列进行回归，分析各频域中的波动溢出效应。我们依然采用BEKK-GARCH模型来分别对 d1、d2、d3、d4、d5、a5 六个尺度上两者收益率序列之间的波动溢出效应进行分析，具体的回归结果如表9所示。

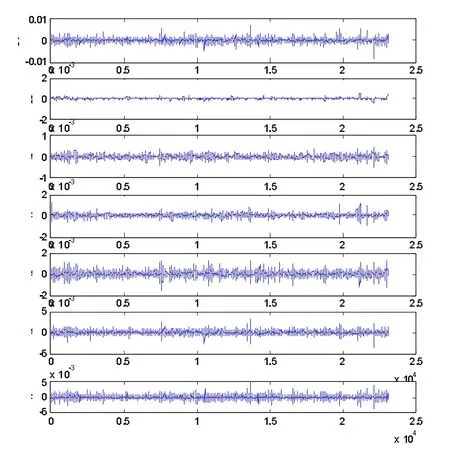
图3 动力煤期货收益率序列小波分析结果

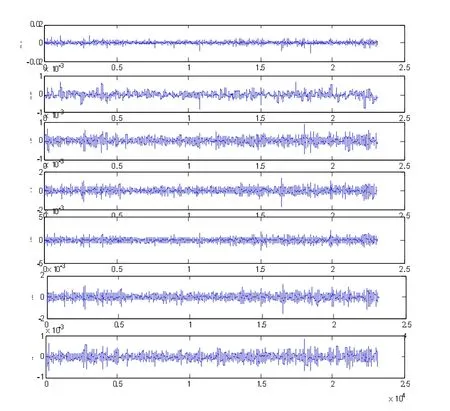
图4 焦煤期货收益率序列小波分析结果

表9 d1、d2、d3、d4、d5、a5 分解尺度上动力煤、焦煤期货BEKK-GARCH回归结果

由回归结果可以看出，d1分解尺度上，对应于动力煤期货对焦煤市场波动溢出的参数都不显著，表明动力煤期货对焦煤期货不存在单向的波动溢出效应。同样，焦煤期货对动力煤期货也不存在单向的波动溢出效应，即在d1分解尺度上，动力煤期货与焦煤期货之间不存在波动溢出效应。

在d2分解尺度上两者存在显著的波动溢出效应。具体来看，α12在15%的显著性水平下显著，而β12在1%的显著性水平下显著，表明动力煤期货对焦煤期货存在显著的波动溢出效应，且主要体现对其条件方差的影响上，同时β12为负，表明动力煤期货对焦煤期货存在负向的GARCH波动溢出效应。另一方面，α21、β21、α21在 5%的显著性水平下显著，且 α21为正，β21为负，说明焦煤期货对动力煤期货存在正向显著的ACRH波动溢出效应和负向显著的GARCH波动溢出效应，即焦煤期货对动力煤期货存在单向显著的波动溢出效应。归纳起来，在d2分解尺度上，动力煤期货与焦煤期货之间存在着显著的双向溢出效应。

同样的道理可以得出，在d3分解尺度上，动力煤期货与焦煤期货不存在波动溢出效应。但与d1分解尺度不同的是，在d3分解尺度上，对应于自身之间的波动传导机制的参数 α11、β11、α22、β22是显著，这表明在动力煤期货市场和焦煤期货市场中存在自身之间的溢出效应。

在d4分解尺度上动力煤期货与焦煤期货之间存在着显著的双向波动溢出效应。且动力煤期货对焦煤期货的波动溢出效应表现为负向的ARCH波动溢出效应以及正向的GARCH波动溢出效应，焦煤期货对动力煤期货的波动溢出效应表现为存在正向的GARCH波动溢出效应及负向的ARCH波动溢出效应。

在d5分解尺度上，动力煤期货与焦煤期货之间也存在着双向显著的波动溢出效应。但α12在1%的置信度水平仍显著，且为负，而β12则非常不显著，说明动力煤期货对焦煤期货的波动溢出效应表现为负向的ARCH波动溢出效应。α21在10%的置信度水平下显著的，而β21则是非常不显著的，这说明焦煤期货对动力煤期货的波动溢出效应表现为负向的ARCH波动溢出效应。

在a5分解尺度上，动力煤与焦煤期货之间不存在显著的波动溢出效应，但两者对自身均存在显著的波动溢出效应。但与d3分解尺度表现不同的是，在a5分解尺度上，对应于动力煤期货对自身的波动溢出效应的系数是0.995 599、0.158 271，两者差距更大，同样对于焦煤期货而言，我们也可以发现同样的现象。

五、结论与展望

动力煤期货与焦煤期货的推出，不仅为我国目前形势严峻的煤炭行业上下游企业带来了福音，同时由于其现货市场关联性显著以及自身的交易量巨大，这也为投资者开展跨品种交易提供了可能性。本文选取动力煤期货与焦煤期货的高频数据作为研究对象，从均值溢出效应和波动溢出效应两个方面来对两者之间的价格联动效应进行分析。

在均值溢出效应方面，通过协整关系检验，表明两者的价格序列存在长期的均衡关系，这与动力煤及焦煤自身的行业特性有关，两者均为周期性行业。之后通过构建稳定VAR模型，表明两者之间存在显著的均值溢出效应。随后在此基础上，通过Granger因果关系检验表明动力煤期货与焦煤期货互为Granger原因，进一步验证了两者之间存在显著的均值溢出效应。最后通过脉冲响应函数分析表明动力煤期货对来自焦煤期货的冲击时的反应是瞬时的并且逐渐趋弱，而焦煤期货对来自动力煤期货的冲击的反应是相对滞后的，并且反应幅度较小。

在波动溢出效应方面，首先对动力煤期货与焦煤期货原始收益率进行ARCHLM检验，结果显示两者都存在高阶的ARCH效应。随后对两个收益率序列构建了二元BEKK-GARCH模型，结果表明动力煤期货与焦煤期货之间存在显著的波动溢出效应。接下来，借用小波多分辨分析理论，将动力煤期货与焦煤期货高频的收益率序列在不同频域上进行分解，分别构建BEKK-GARCH模型，结果表明，在d2、d4、d5三个分解尺度上两者之间的波动溢出效应是显著的，并且三个分解尺度上的表现也各不相同，而在d1、d3以及低频部分a5两者之间不存在任何的波动溢出效应。总体来说，动力煤期货与焦煤期货存在着显著的双向波动溢出效应，但不同频域上的这种波动溢出效应是不同的，这与期货市场自身的运行机制有关，也与当前我国煤炭期货市场成立初期波动较大有关，还需进一步的验证。

当然本文的研究也存在着不足和缺陷之处：第一，动力煤期货市场相比于焦煤期货市场构建时间较晚，而且国际上整体的煤炭期货市场都起步较晚，市场发展相对于其他的股票市场、黄金市场、外汇市场并不成熟，市场波动较大，两者之间的相关性无法得到充分体现，本文的研究并没有考虑到这一点；第二，虽然GARCH类模型在研究波动性溢出方面得到了广泛的应用，但是由于自身假设的不足，在回归中会导致某些信息的缺失；第三，本文在进行小波分解时采用的是db6小波母函数，由于不同小波母函数的着重的性质不同，所以本文的选择难免会导致某些信息的缺失。

[1]LJ Bachmeier，JM Griffin.Testing for Market Integration Crude Oil，Coal and Natural Gas[J].The Energy Journal，2006，27（2）：55-71.

[3]D Manzoor，S Seiflou.Are Crude Oil，Gas And Coal Prices Co Integrated?[J].Iranian Economic Review 2011，15（28）：29-51.

[4]H Mohammadi.Long-run relations and short-run dynamics among coal，natural gas and oil prices[J].Applied Economics，2011，43（2）：129-137.

[5]张同功，雷仲敏.煤炭价格波动的影响因素分析[J].中国能源，2005，27（12）：16-19.

[6]袁桂秋，张玲丹.我国煤炭价格的影响因素分析[J].价格月刊，2009（2）：45-47.

[7]蔡鑫磊.陕西省煤田地质局.目前影响我国煤炭价格的主要因素分析[J].煤炭经济研究，2008（10）：87-90.

[8]战彦领，周敏.国内煤炭产业链整合路径与模式研究[J].煤炭经济研究，2008（12）：21-23.

[9]焦建玲.中国煤炭需求的长期与短期弹性研究[J].工业技术经济，2007，26（4）：108-110.

[10]张志杰，罗世兴.基于VAR与脉冲响应的国内外能源价格波动关系研究[J].中国矿业，2013，22（9）：34-37.

[11]张坤，张丽颖，赵玉，等.能源资源价格长期关系与短期动态调整研究：1985-2011 年[J].自然资源学报，2013，28（6）.

[12]何琬，卢小舒.煤炭价格与石油价格的波动溢出效应分析[J].工业技术经济，2011，30（11）：66-70.

[14]徐进亮，常亮.中国煤炭市场现状剖析与国际煤价走势研究[J].中国人口·资源与环境，2013，23（10）：127-133.

[15]雷强.中国煤炭产业集中度与经济增长的关系研究[J].中国矿业，2013，22（12）：37-42.

[16]Caporale G M，Pittis N，Spagnolo N.Testing for causality in variance an application to eastAsian markets[J].International Journal of Finance and Economics，2002，7（3）：235-245.

[17]Zhong M，Darrat A F，Otero R.Price discovery and volatility spillovers in index futures markets：Some evidence from Mexico[J].Journal of Banking&Finance，2004，28（12）：3037-3054.

[18]杨婷，刘金山.基于小波分析的中美大豆期货价格周期波动关联性研究[J].产经评论，2013，4（2）：150-160.

[19]Brooks C，Ritson R S.A trading strategy based on the lead-lag relationship between the spot index and futures contract for the FTSE 100[J].International Journal of Forecasting，2001（17）：31-44.

[20]严敏，巴曙松，吴博.我国股指期货市场的价格发现与波动溢出效应[J].系统工程，2009（10）：32-38.

[21]封思贤，张兵，李心丹，等.从中国股指期货境外的联动看我国股市定价权[J].金融研究，2010，55（4）：101-114.

[22]Sohrabian B O A.Stock prices and the effective exchange rate of the dollar[J].Applied Economics，1992，24（4）：459-464.

[23]周杰琦，何中正.股票市场与外汇市场之间的溢出效应：基于汇改后数据的实证分析[J].金融理论与实践，2009（9）：8-12.

[24]David P.Simon.The soybean crush spread：Empirical evidence and trading strategies[J].The journal of futures markets，1999：271-289.

[25]李新建，吴春梅，黄敏学，等.我国油脂类期货价格之间的联动分析[J].华中农业大学学报：社会科学版，2011（2）：39-43.

[26]Johnson，L.L.The Theory of Hedging and Speculation in Commodity Futures[J].Review of Economic Studies，1960-10-27：139-151.

[27]Richard A，Stevenson，Robert M，Bear.Commodity Futures：Trends or Random walks?[J].The Journal of Finance，1970：65-8.1

[28]Bahmani-Oskooee，M.，A.Sohrabian.Stock Prices and the Effective Exchange Rate of the Dollar[J].Applied Economics，1992（24）：459-464.

[29]Hengyun Ma，Les Oxley.The integration of major fuel source markets in China：Evidence from panelcointegration tests[J].Energy Economics，2010（32）：1139-1146.

[30]黄玮强，庄新田.中国证券交易所国债和银行间国债指数的关联性分析[J].系统工程，2006，24（7）：62-66.

[31]张兵，刘丹.不同类型主体对大豆期货价格波动的影响分析——基于向量自回归（VAR）模型[J].东南大学学报，2012（14）：30-36.

[32]K Chan，KC Chan，GA Karolyi.Intraday Volatility in the Stock Index and Stock Index Futures Markets[J].Review of Financial Studies，1999（4）：657-684.

[33]Koutmos G，Tucker M.Temporal relationshipsand dynamic interactions between spot and futuresstock markets[J].Journal of Futures Markets，1996（16）：55-69.

[34]Tse Y.Price discovery and volatility spillovers inthe DJIA index and futures markets[J].Journalof Futures Markets，1999（19）：911-930.

[35]邢精平，周伍阳，季峰.我国股指期货与现货市场信息传递与波动溢出关系研究[J].证券市场导报，2011（2）：13-19.

[36]李晓明，万昆，柳瑞禹.国内外煤炭价格波动特征分析——基于GARCH 模型[J].技术经济，2012（8）：65-69.

[37]Ramsey JB，Usikov D，Zaslavsky G M.An analysis of US stock price behavior using wavelets[J].Fractals，1994，3（2）：377-389.

[38]Rua A，Nunes L C.International comovement of stock market returns：A wavelet analysis[J].Journal of Empirical Finance，2009，16（4）：632-639.

[39]宿成建，刘星，刘礼培，等.应用小波分析方法研究沪深股市的溢出效应[J].系统工程学报，2004，19（1）：99-102.

[40]侯守国，张世英.基于小波分析的股市高频互相关研究[J].中国管理科学，2006，4（3）：1-6.

[41]金秀，王佳星，刘烨.基于小波分析的中国A，B股市场相关性研究[J].东北大学学报，2010，1（5）：750-756.

[42]飞思科技产品研发中心.小波分析理论与MATLAB 7实现[M].北京：电子工业出版社，2005：39-40.

[43]Shin T，Han I.Optimal signal multi-resolution by genetic algorithms to support artificial neural for exchange-rate forecasting[J].Expert Systems with Applications，2000，18（4）：257-269.