层次分析法在评估三本院校教师综合能力中的应用

易 强 吕希元

（重庆工商大学融智学院，重庆 400033）

层次分析法在评估三本院校教师综合能力中的应用

易 强 吕希元

（重庆工商大学融智学院，重庆 400033）

本文利用层次分析法对三本独立学院的教师进行年终考核，期望对所考察教师作优劣的排序，以便做到优胜劣汰，选拔能力强的骨干，剔除不称职的教师。

层次分析法 绩效考核 指标 判断矩阵

绩效考核就是对教师全面综合评价，它能够直接反映教师的综合能力，是关系到教师的工资待遇、职称评定和升职的一种手段。

年终考核是对教师进行多指标综合分析的复杂体系。在综合考核过程中需要解决三个方面问题：一是要求避免人的主观因素的影响；二是确定各项指标在考核过程中的相对重要程度；三是对每项指标直接进行定量综合分析。利用层次分析法可以较好地解决此类问题。

层次分析法是融合了定量与定性的系统分析法。它通过对人的思维进行层次化、数量化处理，再用数学方法为分析、决策、预报或控制提供定量的依据。这种数学方法在对解决多因素权重的确定或是多个决策方案的择优排序上相当易于控制而又行之有效。

建立层次分析法，其基本步骤如下：

（1）建立层次分析法的结构模型；

（2）构造判断矩阵；

（3）层次分析单排序和一致性检验；

（4）层次分析总排序和一致性检验。

1.建立层次结构模型

1.1 层次结构图

为了评估三本院校专职教师的综合表现，根据三本院校教师工作特点，我们首先确定绩效考核优劣排序的层次结构如下：

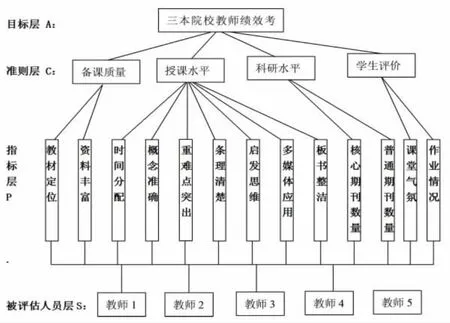
1.2 指标项的确定理由

根据影响三本院校教师绩效考核的各因素，将层次结构图分为三级指标。对三级指标层中13项指标的各项解释如下。

P1教材定位：考察教师在课堂教学中对于教材的把握是否到位；

P2资料丰富：考察教师在备课时资料准备的是否丰富；

P3时间分配：根据三本院校学生的记忆曲线规律，教师应适当安排教学时间，使得学生吸收情况最优；

P4概念准确：考察教师在讲课过程中，对概念的讲解是否准确、清楚，对概念的把握是否恰当；

P5重难点突出：考察教师在授课过程中，对教学大纲中规定的重点、难点把握是否清楚，对重点、难点的讲授安排是否恰当；

P6条理清楚：考察教师在授课过程中对教材内容的安排是否有条理；

P7启发思维：考察教师在授课过程中所采用的教学方法能否有效启发学生的思维，激发学生的想象力和创造力；

P8多媒体应用：考察多媒体教学设施的使用是否恰当，能否使课堂教学取得最大效益；

P9板书整洁：考察教师在授课中所板演的内容能否做到字迹清楚，图形规则，板书工整、有条理；

P10核心期刊数量：考察教师的科研水平，是作为提拔教师的一个重要指标；

P11普通期刊数量：考察教师对于科研方面是否有所投入；

P12课堂气氛：通过对学生的课堂反映、课堂回答等方面综合考评，考察教师对于课堂的整体把握能力；

P13作业情况：通过对学生作业完成情况（包括质量、数量等）的考察，借以评估教师在讲解知识时学生的吸收情况。

2.建立判断矩阵

以重庆工商大学融智学院的五位教师的工作为例，利用层次分析法对其进行绩效考评。

2.1 采取绝对评价法对被评估人员进行综合评价

由学校督导组教师对被考核教师根据上述指标依据进行打分，每一项指标满分为10分，其表格如下：

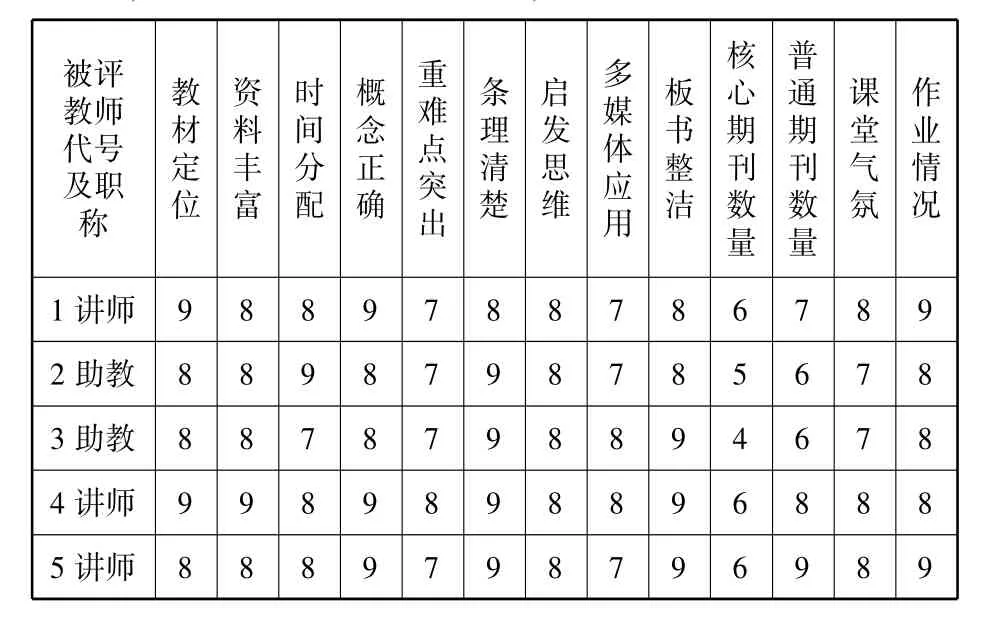
被评教师代号及职称教材定位资料丰富时间分配概念正确重难点突出条理清楚启发思维多媒体应用板书整洁核心期刊数量普通期刊数量课堂气氛作业情况1讲师9 8 8 9 7 8 8 7 8 6 7 8 9 2助教8 8 9 8 7 9 8 7 8 5 6 7 8 3助教8 8 7 8 7 9 8 8 9 4 6 7 8 4讲师9 9 8 9 8 9 8 8 9 6 8 8 8 5讲师8 8 8 9 7 9 8 7 9 6 9 8 9

打分专家职称：（1）副教授、（2）副教授、（3）讲师（重点）、（4）讲师（重点）、（5）教授。

2.2 根据打分的情况进行综合评分

为了避免主观判断明显误差， 首先将被评教师按职称的高低进行分配，并且根据打分专家教师职称的区别，将教授赋予45%、副教授赋予35%、讲师（重点）赋予20%的比例进行分配，即得各项指标的数量评价，再计算综合加权值，即：N=a×W，其中，N：表示绩效考核的综合评价分数；W：表示评分专家教师的权重；a：表示参评人员的权重。

2.3 建立判断矩阵

根据所得的综合测评分数， 针对其指标层中的每个指标，对考核教师进行作两两比较，如：对指标层中P1“教材定位”一项，比较五位教师中第i位和第j位，若第i位教师在“教材定位”方面其分数比第j位教师高2.5分，则记作aij=3，aij的取值如下表：

第i位比第j位教师分数差 0—1 2—3 4—5 6—7 8—9 1 3 5 7 9 aij

若两位考核教师对某指标的表现介于上表中的两者之间，则aij的取值为2、4、6、8。

由此，构造矩阵A1=（aij）5×5称为判断矩阵，同理，对P2“资料丰富”、P3“时间分配”、…、P13“作业情况”，对五位教师分别进行两两比较后，构造出的判断矩阵依次为：

3.对判断矩阵进行层次单排序并进行一致性检验

分别求出判断矩阵A1、A2、A3、…、A13的最大特征值λ1、λ2、λ3、…、λ13及所对应的标准化的正特征值向量，W1、W2、W3、…、W13如下：

并且根据随机一致性比值CR=CI/RI，对矩阵A1、A2、A3、…、A13分别进行一致性检验，发现矩阵A1、A2、A3、…、A13都具有满意的一致性。

4.对五位教师进行优劣排序

该层次模型中的13项指标的权重分别为7%、7%、8%、7%、7%、7%、7%、7%、7%、10%、8%、9%、9%。

由13项指标的权重及所求的特征向量W1、W2、W3、…、W13，用向量表示为：7%·W1+7%·W2+8%·W3+…+9%·W13=（0.14180，0.16927，0.04192，0.54134，0.10567）T

由此可得到这五位教师绩效考评的一个优劣排序为3、2、5、1、4。

5.结语

层次分析法所给出的这一排序方法，并不依赖于每位教师的评估成绩，仅依赖于每一指标下教师两两比较的结果，利用层次分析法不但能够选出参评教师最好的表现者，而且能够对各位参评教师的绩效表现排序，从定性到定量，给出每位教师得分的具体分值。

［1］和珍珍，刘秋静，王超.层次分析法在评估中学课堂讲课效果中的应用.［J］.科教文汇，2010（126）.50-51.

［2］李懿.应用层次分析法提高教学评估的科学性.［J］北京教育学院学报，1992（2）：43－48.

［3］王廋.实用计算机数学模型.［M］.安徽大学出版社，2003（2）：143-154.

［4］杜栋，庞庆华，吴炎.现代综合评价方法与案例精选［M］.北京：清华大学出版社，2008：11-33.

［5］常少健，周文明，张磊.层次分析法在大学生毕业选择中的应用［J］.四川理工学院学报（自然科学版），2007（1）：39-43.

［6］钟强.层次分析法（AHP）在教师课堂教学评价中的应用［J］.聊城大学学报（自然科学版），2007（1）：98-100.

［7］王莲芬.层次分析法引论［M］.北京：中国人民大学出版社，1990.