季节性变动影响下的上海港集装箱吞吐量预测

杜 刚，刘娅楠

（华东师范大学 商学院，上海 200241）

0 引 言

在环球经济一体化的时代背景下，上海港作为我国参与国际贸易的重要港口而存在．并且上海港拥有得天独厚的地理位置，位于我国海岸线与长江“黄金水道”交汇点，以长江三角洲和长江流域为主要经济腹地，集疏网络也十分发达．虽然目前上海港连续多年港口集装箱排名居世界第一．2012年集装箱吞吐量达到3 252．9万TEU，货物吞吐量为7．36亿t，并且上海港的吞吐量在逐年稳步上升．但是，上海港的集装箱竞争力已在下降［1］，显然更为精准的决策和更为有效率的经营对于对上海港非常重要．

国际上一些学者对港口集装箱吞吐量问题进行了研究，Wen－Yi Peng等人采用6种方法对于台湾的3个主要港口的集装箱吞吐量进行了预测，预测结果表明对于台湾港来说该模型是预测月度集装箱吞吐量的最佳模型［2］．这篇文章对于预测国际上其他港口的短期集装箱吞吐量具有借鉴意义．Shih－Huang Chen等人采用3种模型，利用台湾主要港口过去29年的历史数据，对于港口集装箱吞吐量进行了预测，得到结果表明GP模型在这种情况下是最适合的方法［3］．Gang Xie等人利用基于最小二乘支持向量回归（LSSVR）模型的3个混合方法与其他基准方法经过对于港口吞吐量预测方面表现的比较表明，混合方法比单个方法能够达到更好的效果［4］．

国内的学者主要使用神经网络法对于港口集装箱吞吐量进行研究，主要有BP神经网络、RBF神经网络法、GRNN神经网络以及组合模型、灰色组合模型、支持向量机以及SD建模．刘婷和林连通过对厦门港集装箱吞吐量进行预测，发现BP神经网络预测法的预测结果的可靠性最高［5］．程荣等人利用改进的RBF算法对港口集装箱吞吐量进行预测，得到的预测结果更加合理，精度也有了很大的提高［6］．柳艳娇与肖青基于某港的集装箱吞吐量的历史数据，利用改进的GM（1，1）残差模型以及组合预测方法对某港的集装箱吞吐量进行预测，得到的预测结果精度较高［7］．杨中庆等人将GM（1，1）模型与Verhulst模型结合起来形成一种新的灰色组合预测模型，来解决近期、中长期的港口集装箱吞吐量预测问题［8］．戴燚等针对目前常用港口集装箱吞吐量预测方法的局限性，将支持向量机回归方法用于港口吞吐量预测，提出了集装箱吞吐量预测的步骤和相关参数的确定方法［9］．张浩提出了基于最优线性组合的港口集装箱吞吐量预测法，建立线性组合预测模型，用单纯形表法解出加权系数，进行外推预测［10］．赵亚鹏和丁以中运用GRNN神经网络的优点，构建预测模型．预测结果证明，该模型在应用中是有效的，且当样本数据短缺时，预测效果也较佳［11］．宁顺理等人引进系统动力学建模法建立了宁波—舟山港集装箱吞吐量模型，反映了多种不确定因素对港口集装箱吞吐量的影响［12］．

通过国内外的文献综述，发现以上研究很少对港口集装箱的数据的季节性变动进行相应的考虑．实际上季节的变动是影响港口吞吐量的重要因素，本文将采用SARIMA模型对于这种数据波动做出处理，以获得较为精准的预测结果，为港口的成功经营和决策提供相应的依据和指导．

1 模型构建

本文数据来自于上海港2007年至2012年度的上港集团母港集装箱吞吐量的月数据，首先采用ARIMA模型对上海港的集装箱吞吐量进行年度预测，将上述时间序列变成一阶单整数列之后，进行模型估计与预测；接下来利用SARIMA模型处理月度数据中出现的季节性变动．

通过与ARIMA模型预测结果的对比，来验证SARIMA模型是否能够有效地处理上海港2007年至2012年度港口集装箱吞吐量的月度数据中存在的季节性变动．

1．1 单整自回归移动平均模型预测结果

首先，利用Eviews检验时间序列平稳性，对不平稳的时间序列进行差分，直至得到平稳的时间序列，差分次数即为d，差分后得到的平稳时间序列为D（y）．

然后，在平稳时间序列D（y）的基础上建立单整自回归移动平均模型，得到如表1结果．

表1 单整自回归移动平均模型估计结果Tab．1 The model estimation results of autoregressive integrated moving average model

通过上述回归结果（见表1），可以得到：

D（yt）＝－0·008D（yt－1）＋ut－0·655ut－1；

t1＝－0·044，t2＝－5·064；

R2＝0·306，S·E·＝20·657，DW＝1·985·

ARIMA的回归过程会本身会导致R2降低，因此30．6%的拟合优度是可以接受的．

1．2 季节时间序列（SARIMA）模型

季节时间序列模型（SARIMA）的一般形式如下：

Φp（L）Ap（Ls）xt＝Θq（L）BQ（Ls）vt·

其中，s代表观察值的时间间隔，p代表非季节自回归最大滞后阶数，q代表非季节移动平均算子，d代表非季节差分次数，D代表季节差分次数·L代表滞后算子，P是季节回归阶数，Q是季节移动平均阶数，并且分别称ΦP（Ls）与ΘQ（Ls）为季节P阶自回归算子和季节Q阶移动平均算子．

通过SARIMA模型可以消除趋势性和季节性，转化为平稳时间序列进行建模．接下来利用Eviews建立SARIMA模型［13］，并进行预测．

（1）首先要确定d和D，通过差分和季节差分把原序列变换为一个平稳的序列．

通过分析历史数据，可以看出上海港的集装箱吞吐量存在着较为明显的季节波动以及周期，是不平稳的．可以利用差分以及季节差分对该数据进行处理，以得到平稳的时间序列．

结果表明（见表2），在99%的置信度下原历史数据中的季节性变动已经被消除，新的时间序列D（y）是平稳的．

表2 一阶季节差分的ADF检验结果Tab．2 The ADF test results of one season difference

（2）然后利用Eviews对集结时间序列模型参数进行估计，从而建立

模型，估计结果见表3．

Φp（L）Ap（Ls）xt＝Θq（L）BQ（Ls）vt

表3 季节时间序列模型估计结果Tab．3 The model estimation results of seasonal autoregressive integrated moving average model

（1＋0·37L）（1＋0·23L12）ut＝（1－0·41L）（1－0·－0·88L12）vt，

R2＝0·75，DW＝1·99·

R2与单整自回归移动平均模型相比有了明显的提高，但这不能作为判断季节时间序列模型的标准（见表3），要得出结论，还需要进一步的分析．接下来利用估计出的两个模型公式对于上海港未来港口集装箱吞吐量进行预测，对预测结果进行分析．

2 结果分析

首先，季节时间序列模型与单整自回归移动模型相比R－squared以及Adjusted Rsquared都有了明显的提高，而且从极大似然函数值以及残差平方和来看，季节时间序列模型的估计结果也比单整自回归移动模型更好．其次，利用单整自回归移动模型以及季节时间序列模型对估计出的模型进行预测，结果见图1和图2．

从图1和图2可以明显看出，季节时间序列模型拟合效果更好．

本文选取绝对平均误差、均方根误差以及偏倚比例作为定量评价以上两种模型预测效果的指标．从以上两张图可以得到表4．

图1 单整自回归移动模型预测结果与实际值比较图Fig．1 The comparison figure of the prediction and actual results for ARIMA model

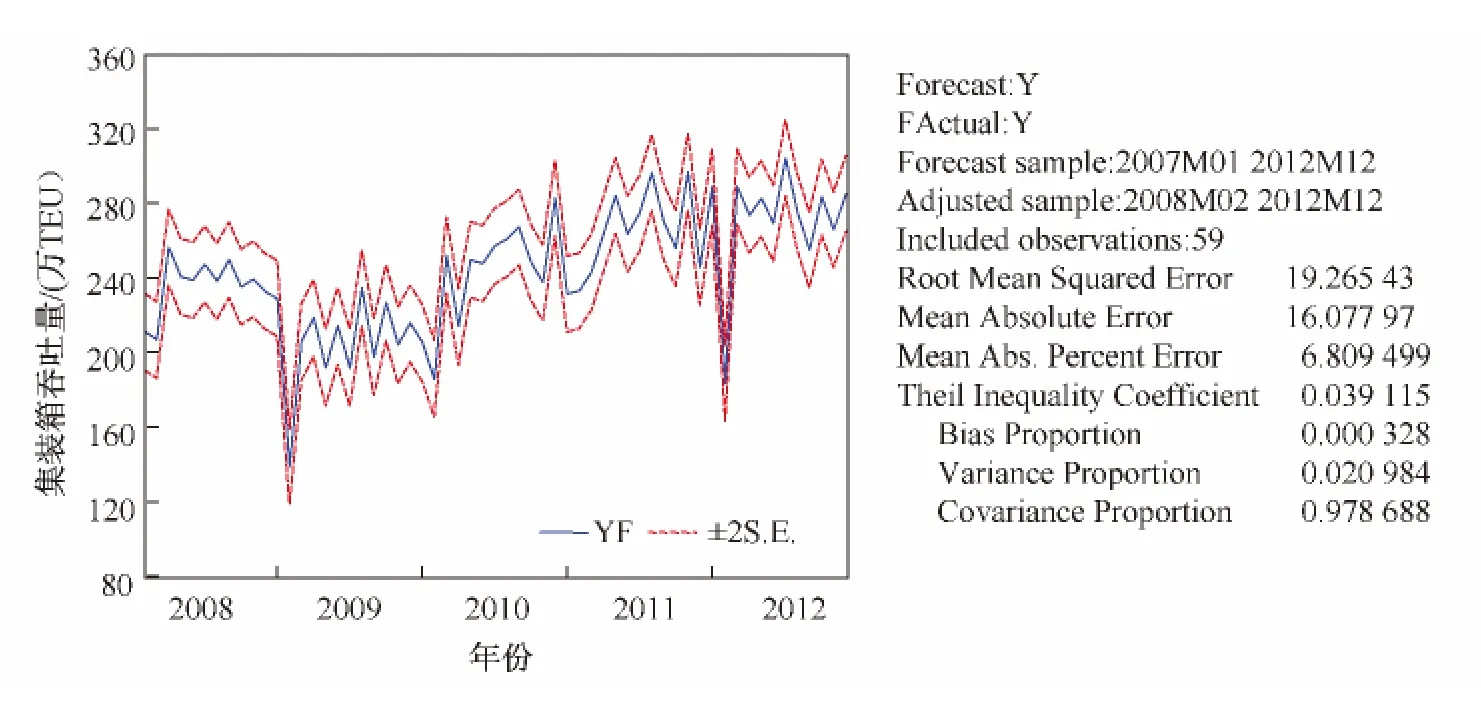
图2 季节时间序列模型预测结果与实际值比较图Fig．2 The comparison figure of the prediction and actual results for SARIMA model

表4 估计模型预测比较Tab．4 The prediction comparison of estimation model

通过表4可以看出季节时间序列模型与单整自回归移动平均模型相比，比较低的绝对平均误差、均方根误差以及偏倚比例，这说明对于上海港来说利用季节时间序列模型预测的效果比利用单整自回归移动平均模型更好．

这也就证实了对于上海港来说基于月度数据利用季节时间序列模型进行港口吞吐量的预测比利用单整自回归移动平均模型进行预测更为准确．上海港港口集装箱吞吐量月度数据确实存在明显的季节变动，而季节时间序列模型能够对该港口的这种季节因素进行很好的处理．

3 建议与展望

3．1 港口集装箱吞吐量预测的应用

准确地预测出上海港口集装箱吞吐量对于上海港的港口建设有着非常重要的战略意义．

从上海港的港口集装箱吞吐量2007年至2012年的历史数据可以看出，上海港的港口吞吐量存在季节性波动．上海港可以通过准确预测港口集装箱吞吐量进行港口设施建设，选择适合的经营策略．

港口集装箱吞吐量的准确结果能够区分港口集装箱吞吐量的长期增减与短期增减．这样管理者就可以运用预测结果配合经营策略以及现金流，制定具体的建设方案．对于港口集装箱吞吐量预测结果出现长期增长的情况，管理者可以增加相关自有港口设备以及仓储面积．如果港口集装箱吞吐量预测结果出现了长期性减少，这是一个不好的信号．管理者需要对自己的经营策略进行审视，发现问题，及时修正．如果港口集装箱吞吐量预测结果显示出短期增加，那么管理者可以考虑进行租赁相关设备以及仓库，增加临时工作人员，增加工作人员加班时间或暂时将部分业务外包．如果港口集装箱吞吐量预测结果出现短期减少，那么管理者可以考虑将部分多余设备暂时租赁以获取收入．

3．2 预测方法的改进

本文只是利用了季节时间序列模型以及单整自回归移动平均模型对上海港港口集装箱吞吐量进行了预测，发现季节时间序列模型更适合对上海港集装箱吞吐量进行预测．季节时间序列模型的预测精度可以通过其他的时间序列分析方法进行改进：①可将三角函数等周期性函数与该模型复合来进一步处理季节性变动，提高预测精确度；②可尝试将不同的模型组合起来，优势互补，用以提高模型预测精确度．

［1］包起帆，江霞．上海港发展面临的问题和未来空间拓展研究［J］．水运工程，2013（3）：16－20．

［2］PENG W Y，CHU C W．A comparison of univariate methods forforecasting container throughput volumes［J］．Mathematical and Computer Modeling，2009，50（7－8）：1045－1057．

［3］CHE S H，CHEN J N．Forecasting container throughputs at ports using genetic programming［J］．Expert Systems with Applications，2010，37（3）：2054－2058．

［4］XIE G，WANG S Y，ZHAO Y X，et al．Hybrid approaches based on LSSVR model for container throughputforecasting：A comparative study［J］．Applied Soft Computing，2013，13（5）：2232－2241．

［5］刘婷，林连．港口集装箱吞吐量预测方法研究［J］．苏州科技学院学报，2011，24（4）：44－46．

［6］程荣，吴国付，张玉洁．改进的RBF神经网络在港口集装箱吞吐量预测中的应用［J］．水运工程，2004（8）：13－20．

［7］柳艳娇，肖青．组合模型在港口集装箱吞吐量预测中的应用［J］．大连海事大学学报，2006，32（3）：25－28．

［8］杨中庆，赵彬彬，廖慧敏．灰色组合模型在港口集装箱吞吐量预测中的应用［J］．水运工程，2006（9）：14－25．

［9］戴燚，王锡淮，肖健梅．支持向量机在集装箱吞吐量上的预测［J］．水运工程，2005（8）：18－39．

［10］张浩．基于最优线性组合的港口集装箱吞吐量预测方法［J］．武汉理工大学学报：交通科学与工程版，2007，31（2）：373－376．

［11］赵亚鹏，丁以中．基于GRNN神经网络的长江干线港口集装箱吞吐量预测［J］．中国航海，2006（4）：90－100．

［12］宁顺理，张亦飞，毛翰宣．宁波—舟山港集装箱吞吐量的SD建模预测［J］．水运工程，2011（4）：58－76．

［13］张健．SARIMA模型在预测中的CPI中的应用［J］．统计与决策，2011（5）：28－30．