基于相似日的光伏发电短期预报模型
(杭州电子科技大学自动化学院,浙江 杭州310081)
0 引 言
随着光伏发电技术的发展,光伏发电的上网电量在电网中占有一定的比例,但光伏发电随着天气的变化而变化,具有不稳定性,对大电网造成了一定的冲击[1],为了降低光伏并网对大电网的冲击,光伏发电功率预测受到了各国学者的重视。近年来,国内外对光伏发电预报的研究工作取得了一定的成果。文献[2-5]使用BP神经网络建立了光伏发电预报模型。其中,文献[2-3]分季节建立预测子模型,均以预测日前一天的功率数据结合天气数据作为输入变量,对于日类型不连续的天气类型精度不高;文献[4-5]对天气类型的分类方法进行了研究,对不同天气类型采用了对应的预测网络。相较于前面的方法有一定的改进。文献[6]中给出了大量的实验数据,验证了在光伏发电预测领域Elman神经网络相比于BP神经网络具有计算速度更快、准确性更高的优点。文献[7]首次将极端学习机方法和相似日方法结合建立了预报模型。由于相同日类型的天气类型的发电功率具有相似性,将相似日应用于光伏发电预报中有一定的实际意义。
针对以上问题,本文综合Elman神经网络方法和相似日的方法进行光伏发电功率预测。首先,通过未来一天的天气预报数据从历史气象数据中选取天气相似日,结合相似日的发电功率数据和相似日与预测日的天气数据建立Elman神经网络预测模型进行光伏发电功率短期预测。
1 光伏发电功率的影响因素
为了分析问题的方便,首先提出以下假设:
1)光伏阵列的安装地理位置固定;
2)光伏阵列在标准测试条件下的转换效率恒定(由于这里探讨的是输出功率的短期预测,可以合理地认为短时间内光伏阵列的效率不受外界环境的影响)。
1.1 季节对光伏阵列输出功率的影响
季节对光伏阵列输出功率有着明显的影响,除去温度以及湿度等微量天气参数的差异外,还会因为太阳辐射度和太阳光与光伏阵列的夹角不同而导致输出不同。本文将一年分为4个时段,即春季2月至4月,夏季5月至7月,秋季8月至10月,冬季11月至次年1月。
1.2 日类型对光伏阵列输出功率的影响
通过对历史数据的统计分析可知,不同天气类型时光伏阵列的输出功率有着较大差异。引用文献[8],单位面积的输出功率为:

式中,ηS为标准测试条件下的转换效率,S为光伏板面积,I为太阳辐射强度,T0为环境温度。
对于安装好的系统,阵列面积固定,并且已经假设阵列的转换效率恒定,故影响光伏阵列发电功率的主要影响因素是太阳辐射强度和温度。太阳辐射强度和温度均随着日类型的不同而不同。本文将日类型分为晴天、晴天偶尔多云、多云偶尔晴天、多云天、阴天、雨天等8种天气类型(其中晴天偶尔多云和多云偶尔晴天又根据晴天时间长短分别分为两种类型)。
1.3 气温对光伏阵列输出功率的影响
当光伏组件温度升高时,工作效率就会降低。由式(1)可以得出气温对输出功率的影响。因此,在气温较高的夏季,光伏发电的输出功率不一定很高,而在气温适中的秋季,如果光照强度高,光伏阵列的输出功率就较高。所以,对于相同的日类型情况,需要考虑到气温对光伏发电功率的影响。
2 光伏发电功率预报模型
本文首先分季节针对天气信息建立日特征向量,并根据相似日选取原理选取对应的相似日,然后结合所选取的相似日的发电功率数据和相似日与预测日的气象数据建立Elman 预测模型进行训练,最后融合4个季节的分立模型形成全年的光伏发电量短期预测模型。
2.1 相似日原理
在大量的已有文献中,发电量的预测模型将预测日前一时间的历史发电数据作为输入变量。这种方案对于日类型连续不变的晴天情况有着较好的准确度,但是当日类型不连续或者出现多云天、雨天等复杂情况时,模型的预测准确度较低。
针对这些不足,本文将一年按照4 季分别建立子模型,并且各个子模型中的日特征向量与气象因素相关,包括气温、辐照时间和日类型指数,设日特性向量为:

为了合理的选取相似日,采用“欧式距离”来描述气象信息的差异度,两日的日特征相似度为:

式中,k为日特征向量的元素序号,xk为日特征向量的第k个元素。一般情况下取归一化因子α =1/max(Dij)。因此,日特征相似度Oij越高,表示两天之间的气象参数等因素越相似。
2.2 预测模型的输入输出层节点的确定
本模型采用16个输入变量,其中相似日7:00 18:00 每个整点发电时间序列作为预测模型的12个输入变量;预测日和相似日的平均温度作为预测模型的2个输入量;预测日和相似日的日类型指数为模型的另外2个输入量。
预测模型的输出是未来一天12个时间整点的发电序列,因此输出层含有12个输出节点。
2.3 预测模型隐含层节点的选取
隐含层节点的选取将直接影响整个网络的性能。本文根据隐含层节点选择经验公式,使用隐含层节点数为14个。
2.4 Elman神经网络模型结构
本文采用的Elman神经网络预测模型拓扑结构图如图1所示,P为输入向量,a1为隐含层输出向量,a2为输出层输出向量。ω1、b1和ω2、b2分别为隐含层和输出层的权值和阈值,ω3为承接层权值,D为反馈支路的延迟单元,logsig为激活函数,n1和n2分别为激活函数的输入向量。
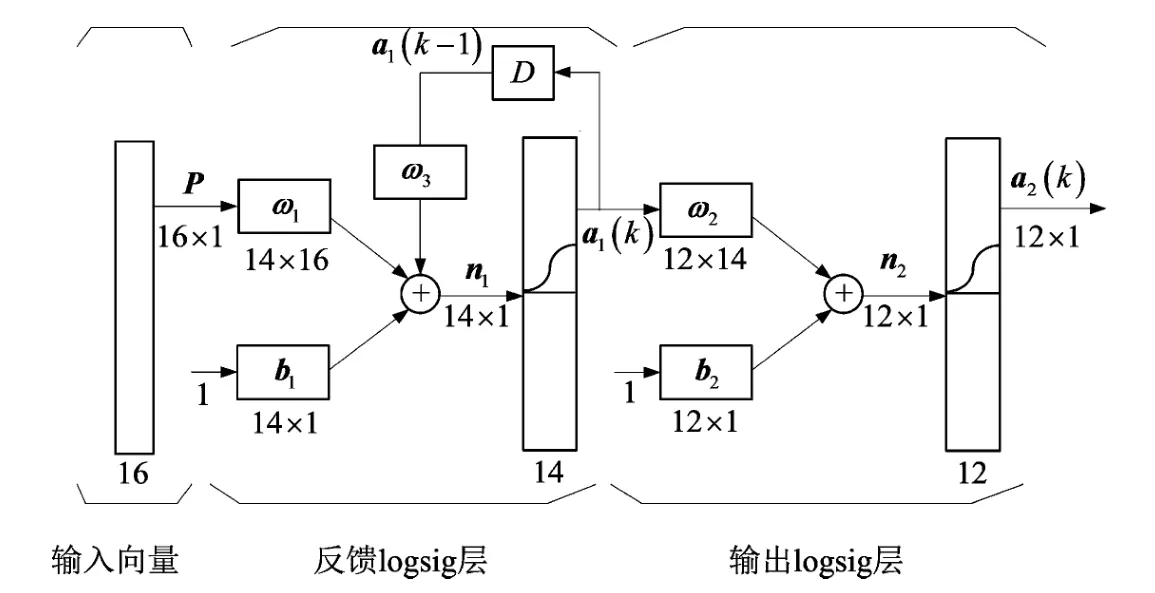
图1 Elman神经网络模型拓扑结构
2.5 预报模型训练和评估
对设计完成的神经网络预测模型需要进行多次训练,一般做法是将一部分数据作为训练集,另一部分数据作为预测集,而样本的数量和质量对于模型的预测精度有着重要影响。
2.5.1 样本的选取
样本数据包括历史的发电量数据、温度数据和日类型指数。在训练样本的选取上,由于所能获得数据的局限性,无法得到精细地影响发电功率的变量(如大气压或湿度等)数据,模型中无法全面考虑这些因素,所以训练样本中存在着一定的噪声,因此需要剔除个别明显异常的样本。
2.5.2 训练样本数据的处理
本文中Elman神经网络每层神经元节点的激活函数采用的是Sigmoid 函数,为了避免神经元饱和,需要对神经网络各输入量进行归一化处理。
2.5.3 预测模型的评估
对发电功率预测模型的评估方法有很多种,如平均绝对误差(MAE)、平均绝对百分比误差(MAPE)等。本文采用最为常用的平均绝对百分比误差(MAPE)作为评估误差的方法。

式中,Pi为光伏阵列输出功率实测值为输出功率预测值;N为预测样本值。
3 光伏发电功率预报模型的实验结果与分析
本文以光伏发电预测的春季子模型为例建立预报模型,利用预测日的日特征向量求取相似日,将相似日的各项数据和预测日的天气预报数据输入到训练好的模型,从而得到预测日的发电量。并针对不同的天气类型分别进行了验证,实验结果如图2所示,图2中为7:00 18:00 之间12个时间整点的发电功率数据。由于光伏阵列的输出功率影响因素比较复杂,本文根据基本的天气数据所得到的预报值与实际发电量还有一些偏差,但仍有较高的参考价值。随着气象预报的数据种类增多以及更多的训练样本数目,预测的精度将会进一步提高。
为了进一步验证本文提出的模型,分别建立了BP神经网络模型和Elman神经网络模型,采用两组数据进行测试,其中一组测试数据使用相似日的功率数据,另一组测试数据使用相同日类型前一日的功率数据。实验结果如表1所示,其中预测模型M1是本文中提出的改进神经网络模型,是结合了相似日的发电功率数据与气象数据的Elman神经网络模型;模型M2是以相似日的发电功率数据结合气象数据作为输入的BP神经网络模型;M3是结合了相同日类型前一日和天气数据作为输入的Elman神经网络模型;M4是相同日类型前一日和天气数据作为输入的BP神经网络模型。

图2 3种天气条件下发电量预测值与实际值对比
由表1分析可知,结合相似日的Elman 预测模型有更高的精度,而且当天气类型是晴天时预测效果比较好。在多云天气条件下,预测效果波动最大,因为多云天气变化比较剧烈,随机性比晴天复杂。同时,雨天的相对均方根误差较大,原因在于相对均方根误差的计算方法,由于误差计算时选用的参考值是实际发电功率均方根,而雨天时的光伏发电功率较小,因此参考值较小,MAPE值相对较大。
总体来说,预测实验结果表明结合相似日的Elman神经网络模型预测效果比较接近实际值,较其他的模型有一定的改进。
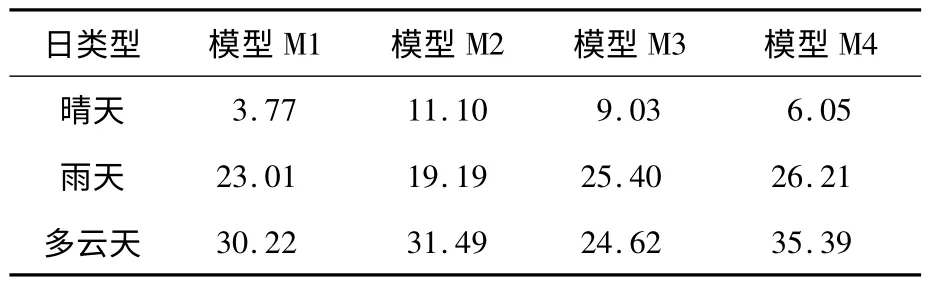
表1 4种预测模型的平均绝对百分比误差%
4 结束语
本文对影响光伏发电系统输出功率的因素进行了分析和选取,结合相似日和Elman神经网络建立了预测模型。由于相似日和预测日的输出功率具有很高的相似度,使用相似日的发电数据结合气象预报数据可以对预测日的发电量进行准确预测。Elman神经网络比BP神经网络具有更好的快速性和准确性,本文将相似日的发电数据和气象数据结合预测日的天气预报数据作为输入,建立了基于相似日的Elman神经网络的预报模型。试验结果表明预测模型有较好的精度,具有一定的有效性。
[1]Paatero J V,Lund P D.Effects of large-scale photovoltaic power integration on electricity distribution networks[J].Renewable Energy,2007,32(2):216-234.
[2]陈昌松,段善旭,殷进军.基于神经网络的光伏阵列发电预测模型的设计[J].电工技术学报,2009,24(9):153-158.
[3]张岚,张艳霞,郭嫦敏,等.基于神经网络的光伏系统发电功率预测[J].中国电力,2010,43(9):75-78.
[4]代倩,段善旭,蔡涛,等.基于天气类型聚类识别的光伏系统短期无辐照度发电预测模型研究[J].中国电机工程学报,2011,31(34):28-35.
[5]王飞,米增强,甄钊,等.基于天气状态模式识别的光伏电站发电功率分类预测方法[J].中国电机工程学报,2013,33(34):75-82.
[6]张艳霞,赵杰.基于反馈型神经网络的光伏系统发电功率预测[J].电力系统保护与控制,2011,39(15):96-101.
[7]刘士荣,李松峰,宁康红,等.基于极端学习机的光伏发电功率短期预测[J].控制工程,2013,20(2):372-376.
[8]Yona A,Senjyu T,Funabashi T.Application ofrecurrent neural network to short-term-ahead generating power forecasting for photovoltaic system[C]//Power Engineering Society General Meeting,2007.IEEE.IEEE,2007:1-6.

